冲击载荷下轨道炮刨削形成机理及仿真分析

金龙文，雷 彬，张 倩

(军械工程学院，河北 石家庄 050003)

刨削的发生会影响轨道炮的发射精度、发射效率并缩短轨道寿命，是电磁轨道炮军事实用化的制约因素之一。美国桑迪亚国家实验室、美国空军技术研究所等对火箭橇轨道刨削进行了大量的理论和仿真研究[1-2]。轨道炮中的刨削与火箭橇上的刨削相比，虽然有相似之处，但是在轨道结构和环境因素等方面存在明显区别。

本文基于电磁轨道炮的发射特点，提出了新的刨削形成机理。并利用ABAQUS有限元仿真软件，对此进行了仿真模拟。最后分析了电枢滑动速度、结构尺寸以及温度变化对刨削的影响。

1 轨道炮刨削形成机理分析

刨削是指电枢和轨道在高速滑动接触时，在轨道表面发生液滴状损伤的现象，其典型形状如图1所示[3]。

1.1 火箭橇和轨道炮关键因素对比分析

通常情况下，火箭橇轨道是单侧多段形状，而且其试验是在野外环境下进行，如图2所示。因此，进行试验时轨道的震动较大，滑块与轨道的相互作用强烈，而且容易受到沙土等环境因素的影响[4]。

而轨道炮中的轨道是双侧对称结构且每条轨道是一个整体，不存在分段形状。此外，轨道炮中的电枢和轨道接触区域类似于炮膛结构，除了其前后开口外其他部分是相对封闭的。因此，在轨道炮的发射过程中，轨道的震动较小，而且周围环境对轨道的影响也会较小。

1.2 微凸体引起的刨削形成机理

美国空军技术研究所等机构对轨道接缝处微断层引起的火箭橇轨道刨削进行了大量的仿真研究[5]，其现象与理论分析和试验观测结果基本吻合。然而，在无轨道接缝的轨道炮上也出现了刨削。因此，轨道接缝不是引起刨削的必要因素。

轨道炮中枢轨之间的摩擦是脉冲大电流、超高速滑动接触条件下的载流摩擦，发射过程中枢轨接触界面温度会急剧变化，界面材料将发生一系列复杂的物理化学反应过程，包括材料的熔化和重新固化、轨道的转捩和烧蚀等。发射过后，轨道表面变得十分粗糙，而且许多大小不一的微凸点或颗粒附着在其表面上。其中大部分与轨道的接触不牢固很容易脱落，而少部分微凸体固化时与轨道成为一体。因此，当重复发射电枢时，由于这些微凸点，电枢和轨道之间有可能发生微观冲击作用，从而导致刨削的形成。

2 仿真模型的建立

2.1 几何参数及枢轨载荷的确定

考虑到引起刨削的关键因素，并结合实际轨道炮的对称性等结构特点，简化并建立了1/2的枢轨接触三维模型，如图3所示。

根据发射后的轨道表面特性，以半径为0.5 mm的半球形微凸体作为引起刨削的诱导因子，具体的几何参数见表1。

表1 仿真模型参数

轨道与电枢间施加的预压力由Marshall的经验公式——“每安培1克”法则[6]得到，即Fpreload=0.01 N/A。根据Kamran Daneshjoo等人[7]推导出的公式可计算出两轨道之间由电磁作用而引起的排斥力为：

(1)

式中：m为自由空间磁导率(真空磁导率为μ0=4π×10-7H/m);I为驱动电流；b为轨道宽度；r为两轨间距。

根据脉冲形成网络放电造成的“平台效应”，假设驱动电流在弹丸发射期间保持在400 kA。通过上述公式和给定参数，可以计算出电枢和轨道之间有效载荷约为2 800 N。

2.2 材料的本构模型及参数

轨道材料取无氧高导性铜，电枢材料取2024-T3铝，以Johnson-Cook模型[8]作为轨道和电枢材料的本构模型。Johnson-Cook模型是一种与应变率和绝热温度相关的模型，忽略了热传导效应。该模型适用于应变率在大范围变化的问题和塑性变形及材料硬化引起的温度变化问题，已在一般的冲击动力学研究中得到了广泛的应用。其流动应力表示为以下形式：

(2)

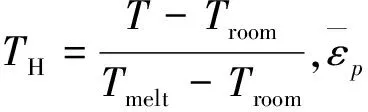
Johnson-Cook模型中的材料参数A、B、n、C、m是通过材料碰撞试验得到的。在本仿真模型中的电枢和轨道材料参数是在总结试验结果、查询手册及经验值后确定的，具体值见表2。

表2 材料参数

3 仿真计算及结果分析

根据以上的结构参数和材料参数，利用有限元软件ABAQUS的显示动力学模块ABAQUS/EXPLICIT对刨削的形成过程进行了仿真计算。

计算过程中未考虑焦耳热和摩擦热的影响，系统的温升只是由冲击载荷下的塑性变形引起。冲击温升后的温度可由下式[9]确定：

(3)

式中：γ0为材料参数，对于普通金属材料，约为2；系数(1+s)/6αT0对于一般固体来说约在10～100的范围。设初始温度T0=300 K、体积压缩应变η=10%时，则温升约为72～147 K。因此当体积压缩应变较小时(η<10%)，其温升可以忽略；然而压缩或变形十分强烈时，温升将按指数形式上升，甚至发生熔化现象。刨削形成过程中，模型中的最高温度变化如图4所示。

由曲线图可以看出，在刨削形成过程中，仅在塑性变形引起的温升作用下就发生了材料的熔化。这一点与无载流的火箭橇滑轨摩擦中观察到的试验现象相吻合。在2 000 m/s滑动速度、2 800 N枢轨载荷下，刨削的形成过程如图5所示。

图中所示为刨削形成过程中Mises应力截面图。从图中可以看出，在电枢的冲击载荷作用下，由微凸体引起的碰撞在局部形成高压作用区域。随着电枢的继续滑动，这个区域逐渐扩大，刨槽便开始形成。基于以上仿真模型，在不同的滑动速度、材料初始温度和枢轨载荷下进行了刨削仿真计算，并对其结果进行了分析。

3.1 枢轨相对滑动速度

高速是产生刨削的重要起因之一，仿真计算结果表明，不同的滑动速度将导致不同的刨槽大小和形状。在800 m/s和2 400 m/s滑动速度、初始温度在25 ℃下发生的刨槽形状，如图6所示，图中显示为轨道上表面的俯视图。

从图中可以看出，在(b)图中刨槽形成时的张角明显比(a)图中的大，刨槽也更宽，轨道受到的损伤也更严重。此外，刨削发生的位置也发生了明显的变化。在800 m/s滑动速度下，离微凸体大约5 mm处才开始发生刨削；而在2 400 m/s滑动速度下，在微凸体处就开始发生了刨削，这现象有待进一步研究。

3.2 枢轨材料初始温度

温度是引起材料性能变化的重要因素之一，为了确定温度变化对刨槽形状的影响，在不同的初始温度下进行了刨削的对比仿真，结果如图7所示。

比较两张图可以发现，(b)图中有明显多一块刨削区域。这表明，初始温度的增大将导致更严重的刨削损伤。而且刨削发生的位置也有提前的趋势，在(b)图中的位置与(a)图中相比，大约提前2 mm。因此，材料的高温特性及轨道的散热性能的研究，对轨道抗刨削技术至关重要，应给予重视。

3.3 枢轨界面载荷

为了保证轨道炮发射过程中电枢与轨道之间良好的电接触性能，需要在轨道和电枢之间加载预压力。图8表示在不同的枢轨载荷下刨槽尺寸的变化特点。从图中可以看出，随着枢轨载荷的增加，刨槽长度有增大的趋势，但是不明显，而刨槽深度未发生明显变化。

除此之外，通过仿真发现刨槽的长度与电枢的长度有直接关系。电枢越长，刨槽也越长，即刨槽长度与发生刨削过程中枢轨之间有效接触长度有关。

4 结束语

针对电磁轨道炮的发射特点，提出了轨道表面微凸体引起的刨削形成机理，并在不同的参数和载荷条件下进行了仿真研究。发现轨道表面的微凸体确实能够成为引起刨削的诱导因素；刨槽的尺寸主要取决于枢轨间相对滑动速度和电枢长度，而与枢轨界面载荷关系不大；材料的初始温度越高，发生的刨削越严重，而且其发生的位置也有变化。

本文所提出的刨削形成机理能够较好地描述了轨道炮刨削形成特点及各影响因素的作用规律，可以为电磁轨道炮抗刨削技术研究提供新的研究思路。

参考文献(References)

[1] TACHAU R D M, YEW C H, TRUCANO T G. Gouge initiation in high-velocity rocket sled testing[J]. International Journal of Impact Engineering, 1995, 17(4):825-836.

[2] LAIRD D J. The investigation of hypervelocity gouging[D]. Ohio:Air Force Institute of Technology, 2002.

[3] MCNAB I R, CRAWFORD M T, SATAPATHY S S, et al. IAT armature development[J]. IEEE Transactions on Plasma Science, 2011, 39(1):442-451.

[4] CINNAMON J D, PALAZOTTO A N, BRARET N S. Further refinement of material models for hypervelocity gouging impacts[C]. Newport: 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2006.

[5] CINNAMON J D, PALAZOTTO A N. Analysis and simulation of hypervelocity gouging impacts for a high speed sled test[C]. Honolulu: 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2007.

[6] RICHARD A.MARSHALL, WANG Ying. Railguns: their science and technology[M]. Beijing: China Machine Press, 2004.

[7] DANESHJOO K, AHMADI R, GHASSEMI M, et al. Dynamic response and armature critical velocity studies in an electromagnetic railgun[J]. IEEE Transactions on Magnetics, 2007,43(1):126-131.

[8] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C].The Hague：Proceedings of the 7th International Symposium on Ballistics, American Defense Preparation Organization，1983：541-547.

[9] 唐志平.冲击相变[M].北京：科学出版社，2008.

TANG Zhi-ping. Shock-induced phase transition[M]. Beijing: Science Press, 2008. (in Chinese)