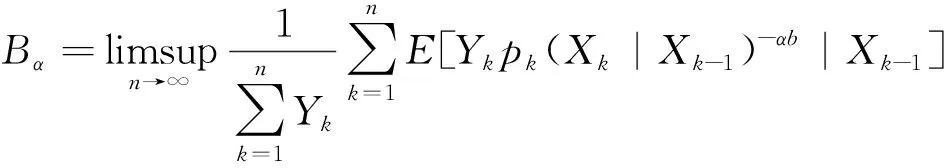任意非齐次可列马氏信源关于广义随机选择系统的广义Shannon-McMillan定理
2012-11-21王康康宗德才黄辉林
王康康, 宗德才, 李 芳, 黄辉林
(1.江苏科技大学 数理学院, 江苏 镇江 212003) (2.常熟理工学院 计算机科学与工程学院, 江苏 常熟 215500) (3.安徽师范大学 数学与计算科学学院, 安徽 芜湖 241000) (4.上海交通大学 数学系, 上海 200240)
设(Ω,F,P)为一概率空间,设{Xn,n≥0}是定义在该概率空间上并于字母集S={s1,s2,…}上取值的任意信源,其联合分布为
P(X0=x0,…,Xn=xn)=p(x0,…,xn)>0
xi∈S, 0≤i≤n
(1)

(2)
式中:log为自然对数,fn(ω)称为{Xi,0≤i≤n}的相对熵密度.
如果{Xn,n≥0}为非齐次马氏信源,其初始分布与转移概率分别为:
(q(s1),q(s2),…,q(sn),…),q(si)>0,si∈S
(3)
Pn=(pn(sj|si)),pn(sj|si)>0,si,sj∈S,n≥1
(4)
式中:pn(sj|si)=P(Xn=sj|Xn-1=si)n≥1
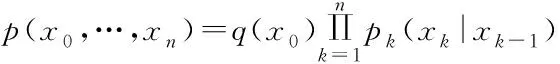
(5)
则非齐次马氏信源{Xn,n≥0}的相对熵密度为:
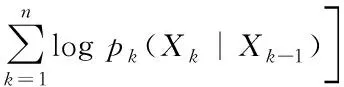
(6)
式中:log 为自然对数,fn(ω)称为{Xi,0≤i≤n}的相对熵密度.
定义1我们给出广义随机选择的概念,先给出一组定义在Sn+1(n=0,1,2,…)上的非负实值函数列fn(x0,…,xn).
令Y0=y(y为任意实数),Yn+1=fn(X0,…,Xn),n≥0;fn(x0,…,xn)称为选择函数.如果{Yn,n≥0}在区间[0,b]取值,{Yn,n≥0}称为广义赌博系统或广义随机选择系统.而传统的赌博系统或随机选择系统在两点集{0,1}中取值.
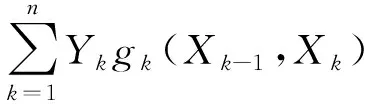
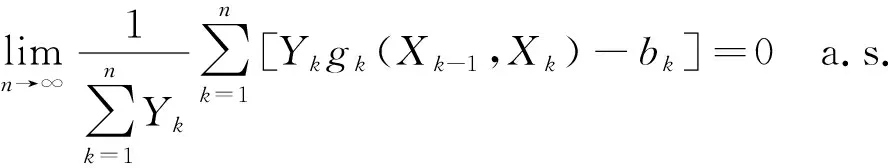
(7)
定义2设{Xn,n≥0}为如上定义的非齐次马氏信源,{Yn,n≥0}为随机选择系统,称

(8)
为非齐次马氏信源{Xn,n≥0}关于随机选择系统的相对熵密度,也称其为广义相对熵密度.显然,当Yk≡1,0≤k≤n时,该广义相对熵密度Sn(ω)即为一般的相对熵密度fn(ω).
关于fn(ω)的极限性质是信息论中的重要问题,在信息论中称为Shannon-Mcmillan定理或信源的渐近均匀分割性(简称S-M定理),它是信息论中编码的基础.文献[1]中首先证明了齐次遍历马氏信源的S-M定理.文献[2-3]则证明了平稳遍历信源的S-M定理.文献[4]考虑了字母集为可列集的情况.以后又有许多作者将上述结果推广到一般的随机过程[5-6].文献[7]中通过任意信源与无记忆信源比较,用特有的分析方法给出了一类任意离散信源相对熵密度用不等式给出的强极限定理,也称为小偏差定理.文献[8]中研究了有限状态集合下非齐次马氏信源的一类Shannon-Mcmillan定理.文献[9-12]中分别讨论了任意信源和m阶马氏信源的一类强偏差定理和任意信源关于赌博系统的若干强极限定理.
文中的目的是将文献[8]的结果推广到广义随机选择系统的情况.即通过构造相容分布和非负上鞅的方法,研究非齐次马氏信源关于广义赌博系统的一类广义Shannon-Mcmillan定理.并由此得出已有的非齐次马氏信源的Shannon-Mcmillan定理.文中将文献[7]中所用的方法加以改进,并作为推论得到了文献 [8] 的主要结果.
定义3设

(9)
称H(pk(s1|Xk-1),pk(s2|Xk-1),…)为Xk关于Xk-1的随机条件熵.
1 主要定理
定理1设{Xn,n≥0}是具有初始分布(3)与转移概率(4)并取值于可列集S的非齐次马氏信源,Sn(ω)与H(pk(s1|Xk-1),pk(s2|Xk-1),…)分别由式(8,9)定义,{Yn,n≥0}如前定义.设α>0,
(10)
(11)
则有
a.s.ω∈D
(11)
证明: 考虑概率空间(Ω,F,P), 设λ为任意实数,设
Qk(λ)=E[pk(Xk|Xk-1)-λYk|Xk-1=xk-1]=
(13)
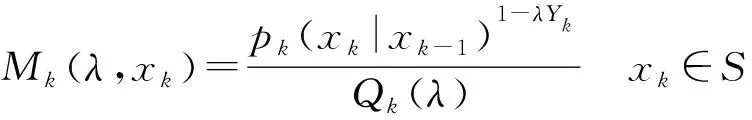
(14)
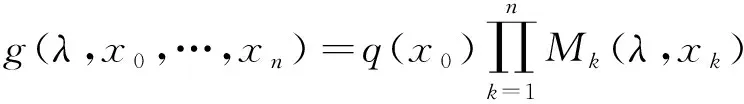
(15)
由式(13,14,15)可知:
g(λ,x0,…,xn-1)=
g(λ,x0,…,xn-1)=
g(λ,x0,…,xn-1)
(16)
于是有g(λ,x0,…,xn),n=1,2,…是Sn上的一族相容分布.令
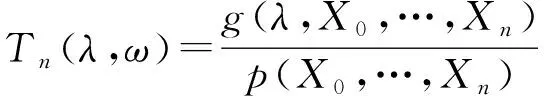
(17)
由于{Tn(λ,ω),n≥1}是a.s.收敛的非负上鞅[4].故由Doob鞅收敛定理有
(18)
因而由式(10,18)有
(19)
由式(5,13~15,17,19)有
logE(pk(Xk|Xk-1)-λYk|Xk-1)]≤0
a.s.ω∈D
(20)
易知由不等式
有
(21)
又由不等式logx≤x-1.(x≥0)及式(11,20,21),且注意到
当0<|λ| pk(Xk|Xk-1)-|λ|b|Xk-1= pk(Xk|Xk-1)(α-|λ|)bpk(Xk|Xk-1)-αb|Xk-1]≤ (22) 当0<λ a.s.ω∈D (23) 取0<λi<α(i=1,2,…),使得λi→0(i→∞)则对一切i,由式(23)有 a.s.ω∈D (24) 类似的,当-α<-t<λ<0时,利用式(22)可证有 a.s.ω∈D (25) 由式(24,25)即证有 logpk(Xk|Xk-1)|Xk-1)]=0 a.s.ω∈D (26) 又注意到 H(pk(s1|Xk-1),pk(s2|Xk-1),…)= E(-logpk(Xk|Xk-1)|Xk-1). 于是由式(8,26)便有 a.s.ω∈D (27) 从而,定理证毕. 推论1设{Xn,n≥0}是具有分布(1)的任意信源,fn(ω)与H(pk(s1|Xk-1),pk(s2|Xk-1),…)分别由式(6,9)定义.设α>0, (28) 则有 (29) 定理2设{Xn,n≥0}是具有初始分布式(3)与转移概率式(4)的非齐次马氏信源,并于字母集S={s1,s2,…,sN}上取值,Sn(ω)由式(8)定义,{Yn,n≥0}如前定义.设 Hk(pk(s1|Xk-1),…,pk(sN|Xk-1))= 则有 a.s.ω∈D (30) (31) 所以式(11)自然成立.由式(12)即得式(30)式成立. 推论2[8]设{Xn,n≥0}是如上定义的非齐次马氏信源,fn(ω)如式(6)定义, 则有 pk(sN|Xk-1))=0 a.s. (32) 证明: 定理2中令Yn≡1,n≥0,即有 该推论便是文献[8]中的定理2. 推论3设{Xn,n≥0}为无记忆信源.其中fn(ω)由式(2)定义.设H(pk(1),…,pk(N))表示分布(pk(1),…,pk(N))的熵.即 (33) 则有 (34) 证明: 由推论2知这时pk(Xk|Xk-1)=pk(Xk),从而 Hk(pk(s1|Xk-1),…,pk(sN|Xk-1))= H(pk(1),…,pk(N)) 由式(32)即得式(34)成立. 定理3设{Xn,n≥0}是具有初始分布式(3)与转移概率式(4)并取值于可列集S的非齐次马氏信源,Sn(ω)与H(pk(s1|Xk-1),pk(s2|Xk-1),…)分别由式(8,9)定义,{Yn,n≥0}如前定义.设α>0,0 Xk-1]<∞ a.s. (35) 则有 a.s.ω∈D (36) 证明: 由式(11,35),简记pk(Xk|Xk-1)=pk.则有 (37) 由定理1即可得式(36)成立. [1] Shannon C E. A mathematical theory of communication [J].BellSystemTechnicalJournal,1948,27(3): 379-423. [2] Mcmillan B. The basic theorem of information theory[J].AnnMathStatist, 1953,24:196-219. [3] Breiman L. The individual ergodic theorem of information theory[J].AnnMathStatist, 1957, 28: 809-811. [4] Chung K L. The ergodic theorem of information theory [J].AnnMathStatist, 1961,32(2): 612-614. [5] Kieffer J C. A simple proof of the Moy-Perez generalization of Shannon-Mcmillan theorem[J].PacificJMath, 1974,51(2):203-204. [6] Algoet P, Cover T. A sandwich proof of Shannon-Mcmillan theorem[J].AnnProbab, 1988,16: 899-909. [7] 刘文,杨卫国.关于Shannon-Mcmillan定理的若干研究,数学物理学报[J].1994,3:337-345. Liu Wen, Yang Weiguo. Some research on Shannon-Mcmillan theorem [J].ActaMathematicaScientia, 1994,3: 337-345.(in Chinese) [8] Liu Wen, Yang Weiguo. An extension of Shannon-Mcmillan theorem and some limit properties for nonhomogeneous Markov chains[J].StochasticProcessandtheirApplications, 1996,61(1):129-145. [9] Wang Kangkang, Yang Weiguo. A class of Shannon-Mcmillan approximation theorems for arbitrary discrete information source [J].JournalofMathematicalResearchandExposition, 2007, 27(4): 719-727. [10] Wang Kangkang. A class of Shannon-Mcmillan theorems for arbitrary discrete information source on the gambling system[J].PureandAppliedMathematics, 2008, 28 (2): 353-357. [11] Wang Kangkang, Ye Hui, Li Fang. A class of generalized Shannon-Mcmillan theorems for arbitrary discrete information source [J].JournalofMathematics, 2011, 31(2): 307-313. [12] Wang Kangkang. Some research on Shannon-McMillan theorem formth-order nonhomogeneous Markov information source[J].StochasticAnalysisandApplications, 2009, 27 (6):1117-1128.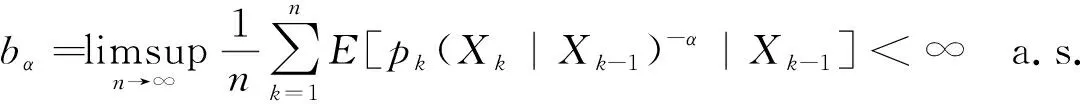
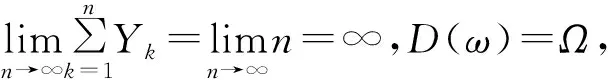
2 状态有限空间下的若干随机Shannon-McMillan定理
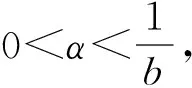

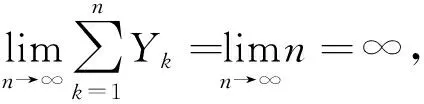
3 衍生结论