多传感器序贯势分布概率假设密度滤波

章 飞, 孙 睿

(江苏科技大学 电子信息学院, 江苏 镇江 212003)

在多传感器多目标跟踪系统中,对于目标状态的估计是通过融合来自多个传感器的数据得到的.融合多个传感器的数据能够提高跟踪系统的性能,然而,多传感器多目标跟踪问题至今仍然是具有挑战性的问题,这些挑战源于目标数目的不确定性、目标与量测之间数据关联的复杂性等问题[1]．近年来,针对多传感器多目标跟踪问题,研究了很多数据融合的方法[2-4],主要分为集中式融合、分布式融合以及混合式融合3类,而这3类方法一般都需要解决数据关联问题,计算量较大,特别是在杂波环境中，传感器和目标数量较大时会出现计算上的组合爆炸,其计算时间是不可接受的[5]．

近年来,随机集方法成为多传感器多目标跟踪的一个新的研究方向．文献[6]在随机集理论的框架下提出了一种概率假设密度(probability hypothesis density, PHD)滤波,该滤波方法在单目标状态空间操作,完全避免了数据关联的计算,大大减少了计算量．而PHD滤波是在单传感器情况下提出的,对于多传感器情况不适用.文献[7]基于序贯滤波的方法将PHD滤波推广到多传感器情况,并给出了粒子滤波的算法实现,但基于粒子滤波的算法实现仍然具有计算量大的不足,且其中基于聚类技术的目标状态的提取方法不可靠,对于目标数目的估计不稳定[8].文献[5]提出了一种基于高斯混合实现的序贯概率假设密度滤波(Gaussian mixture sequential PHD, GMSPHD)算法,增加了多传感器多目标跟踪的序贯PHD滤波的稳定性和可靠性．但在目标数目较大的情况下,PHD滤波对目标数目的估计方差也较大,而文献[9] 提出的势分布概率假设密度(Cardinalized PHD, CPHD)滤波通过同时传递PHD函数和目标数目分布即势分布的概率密度函数,提高了目标估计的精度和稳定性[10]．

文中利用序贯滤波的方法将单传感器的高斯混合势分布概率假设密度滤波扩展到多传感器情况,称为高斯混合序贯势分布概率假设密度(Gaussian mixture sequential CPHD, GMSCPHD)滤波．仿真实验说明了文中的GMSCPHD滤波算法在多目标情况下良好的跟踪性能．

1 高斯混合序贯势分布概率假设密度滤波

1.1 问题描述

多传感器多目标跟踪问题可以在随机有限集框架下建模[6]．设χ为单目标状态空间,则k时刻多目标状态表示为Xk={xk,1,xk,2,…,xk,Nk}∈F(χ),其中,F(χ)为状态空间χ的所有有限子集的集合,Nk为目标数目．对于k-1时刻的多目标状态Xk-1,目标状态为xk-1∈Xk-1的单个目标在k时刻的幸存概率为pS,k,消失概率为1-pS,k．设Sk(xk-1)为k-1时刻存在的目标在k时刻仍然存在的目标随机有限集状态,Bk|k-1(xk-1)为k-1时刻状态为xk-1的目标在k时刻发生目标衍生的随机有限集状态,Γk为k时刻新生目标的随机有限集状态．给定k-1时刻多目标状态Xk-1,则k时刻多目标随机有限集状态Xk可以描述为[5-6]:

Xk=∪Sk(xk-1)∪∪Bk|k-1(xk-1)∪[Γk]

(1)

随机有限集Xk包括了多目标跟踪问题的所有方面,如目标数目随时间的变化,目标的衍生、新生等[5]．

(2)

假设有Q个传感器,则k时刻所有量测的随机有限集描述为：

(3)

随机有限集Zk包括了传感器的所有特性,如量测噪声,传感器的观测范围,杂波干扰等[5]．

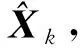
1.2 高斯混合序贯CPHD滤波递推算法

势分布概率假设密度滤波传递的是概率假设密度和目标数目分布的概率密度,记vk|k-1和pk|k-1分别为预测多目标状态的概率假设密度函数(强度函数)和目标数目分布的概率密度函数(目标势分布概率密度函数),记vk和pk分别为后验多目标状态强度函数和目标势分布概率密度函数．

多传感器多目标高斯混合CPHD滤波是在多目标运动模型和观测模型都是线性高斯假设的前提下得到的,并且目标的新生、消失和检测也都是基于线性高斯假设的[8]．

设每一个目标有如下的线性高斯动态模型

fk|k-1(x|ζ)=N(x;Fk-1ζ,Qk-1)

(4)

式中：N(·;m,P)为均值为m，协方差矩阵为P的高斯分布概率密度函数；Fk-1为目标的状态传递矩阵；Qk-1为过程噪声协方差矩阵．设有Q个传感器,则每个传感器的量测函数也满足线性高斯模型

(5)

设目标幸存概率和检测概率都是状态独立的,即pS,k(x)=pS,k,pD,k(x)=pD,k,杂波强度函数为κk(·),新生目标的随机集强度函数具有高斯混合形式：

(6)

对于多传感器情况,可以顺序使用文献[10]的单传感器高斯混合势分布概率假设密度(GMCPHD)滤波,利用来自多个传感器的量测进行滤波更新,从而获得比单传感器更好的多目标跟踪性能[5]．单传感器GMCPHD滤波递推算法参考文献[10],这里仅简单给出GMCPHD滤波算法的预测和更新部分,具体如下：

GMCPHD滤波预测部分:设k-1时刻的后验强度函数vk-1和势分布密度函数pk-1已知,且vk-1具有如下高斯混合形式：

(7)

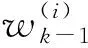
pS,k)l-i

(8)

(9)

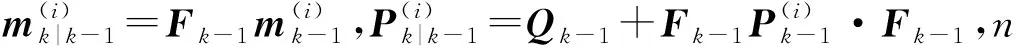
GMCPHD滤波更新部分:假设k-1时刻的预测强度函数和势分布密度函数已由预测部分求得,且预测强度函数具有高斯混合形式：

(10)

则k时刻更新的势分布密度函数和具有高斯混合形式的强度函数为：

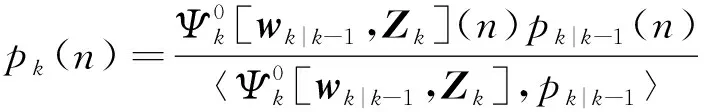
(11)

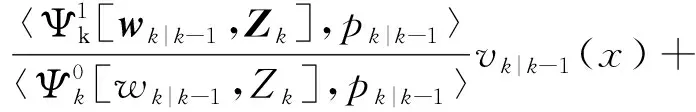
(12)

(13)

(14)

(15)

式中：

(16)

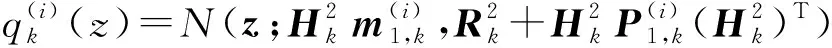
(17)

(18)

(19)

(20)

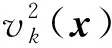
(21)

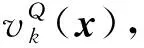
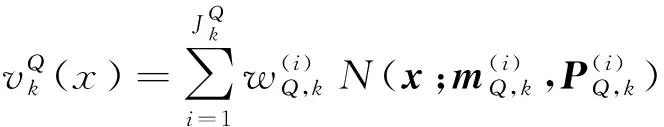
(22)

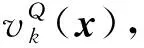
(23)

对于目标数目的估计则为：

(24)

综上所述,高斯混合多传感器序贯CPHD(GMSCPHD)滤波的递推算法与单传感器情况类似,只是在更新阶段利用多传感器的量测序贯的更新概率假设密度,且在每一步更新之后可以利用文献[8]的剪枝与合并技术去掉小权值的高斯分量和合并分布非常接近的高斯分量,以减少计算量．在多传感器多目标跟踪问题中,如果初始的先验强度函数具有高斯混合形式,那么经过序贯滤波后的后验强度函数仍然具有高斯混合形式[5]．

采用扩展Kalman滤波器和无迹Kalman 滤波器,可以得到当目标动态模型和观测模型为非线性情况的GMSCPHD滤波算法．

2 仿真结果和分析

仿真实验中,比较了文中的GMSCPHD滤波算法与文献[5]的GMSPHD滤波算法以及单传感器的GMPHD滤波算法和GMCPHD滤波算法在多目标情况下的跟踪性能,给出了各算法的多目标位置估计精度和目标数目估计精度以及单次运行时间的比较．仿真实验的电脑台式机硬件平台为Intel Pentium Dual CPU E2200 2.22GHz,2GB内存；软件环境为Matlab7.0．

xk+1=A(ωk)xk+Γwk

(25)

ωk+1=ωk+Δuk

式中：状态转移矩阵

设有2个传感器对监视区域内的目标进行跟踪,传感器i的观测方程为：

(26)

系统过程噪声和量测噪声均为相互独立的零均值高斯白噪声,高斯过程噪声标准差为σw=1.0 m/s2,量测噪声标准差为σβ=0.05 rad/s,σr=10 m;杂波的poisson RFS强度函数κk(z)=λcVu(z),其中λc=1.25×10-5m-2,为单位容积内杂波的个数(杂波强度),V为观测区域的体积,u(z)为在观测区域上服从均匀分布的概率密度函数．新生目标强度函数的高斯分量权值均为0.1,不考虑目标的衍生．目标幸存概率pS,k为0.9,目标检测概率pD,k为0.9．利用文献[8]中的剪枝操作,设权值阈值Ts=10-5,合并阈值U=4m,允许的最大高斯分量数Jmax=200．

在上述条件下,经过100次Monte Carlo仿真,得到了GMSCPHD滤波算法和GMSPHD滤波算法以及单传感器的GMPHD滤波算法和GMCPHD滤波算法对目标位置估计精度和目标数目估计精度的比较,如图1～6,并且将各种滤波算法对于目标数目估计的平均误差以及平均单次运行时间分别在表1，2中进行了比较．

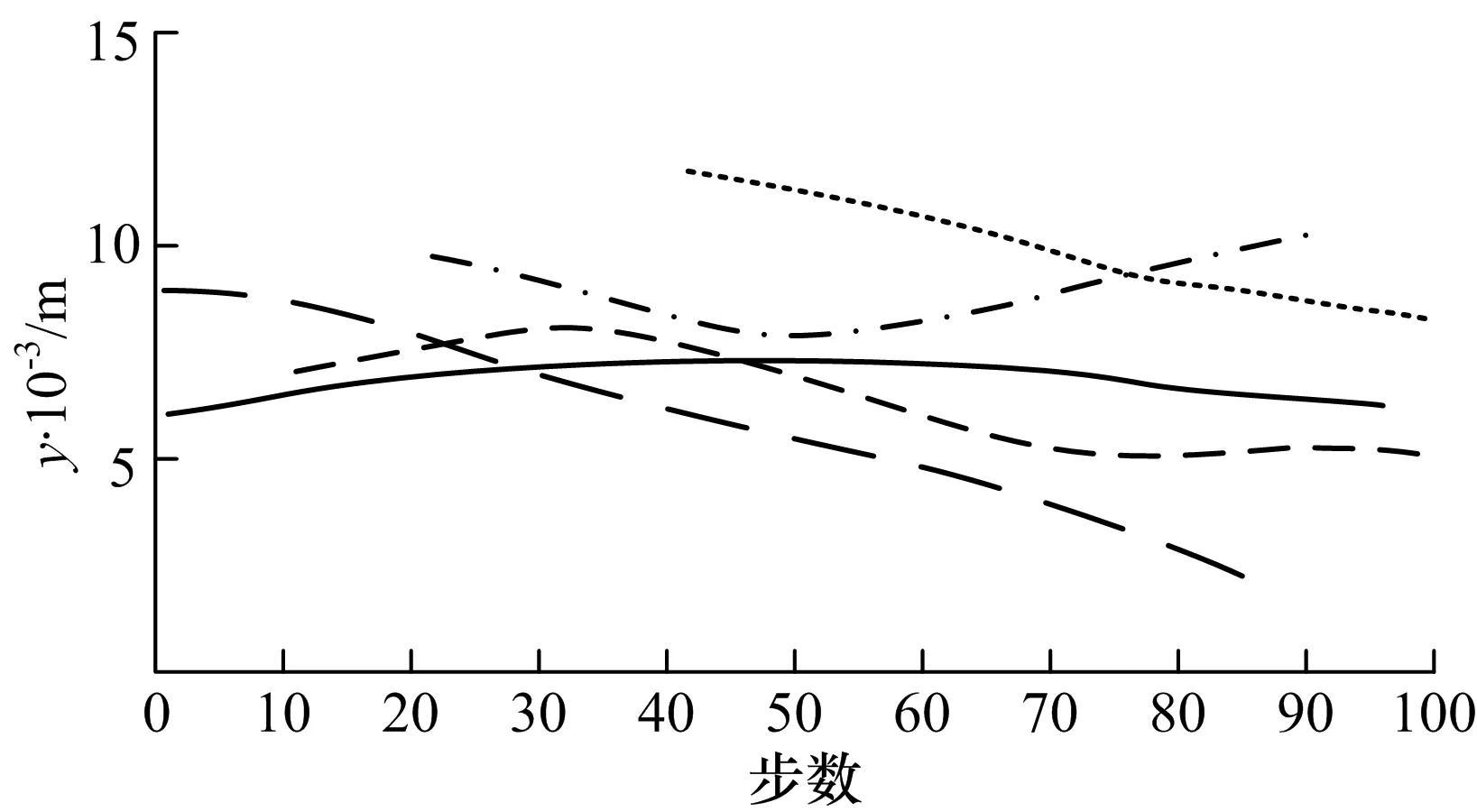
图1 GMPHD滤波位置估计

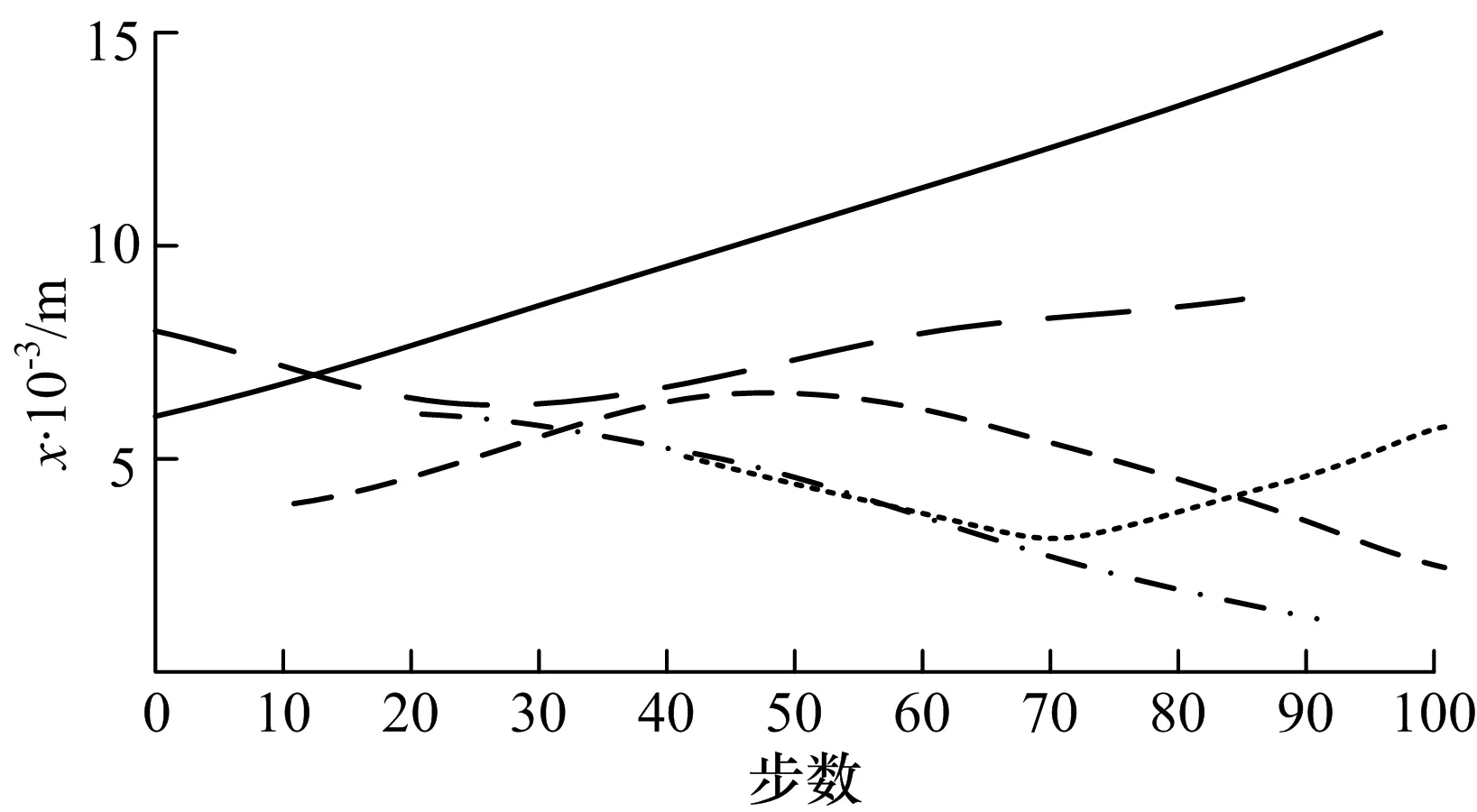
图2 GMCPHD滤波位置估计

图3 GMSPHD滤波位置估计

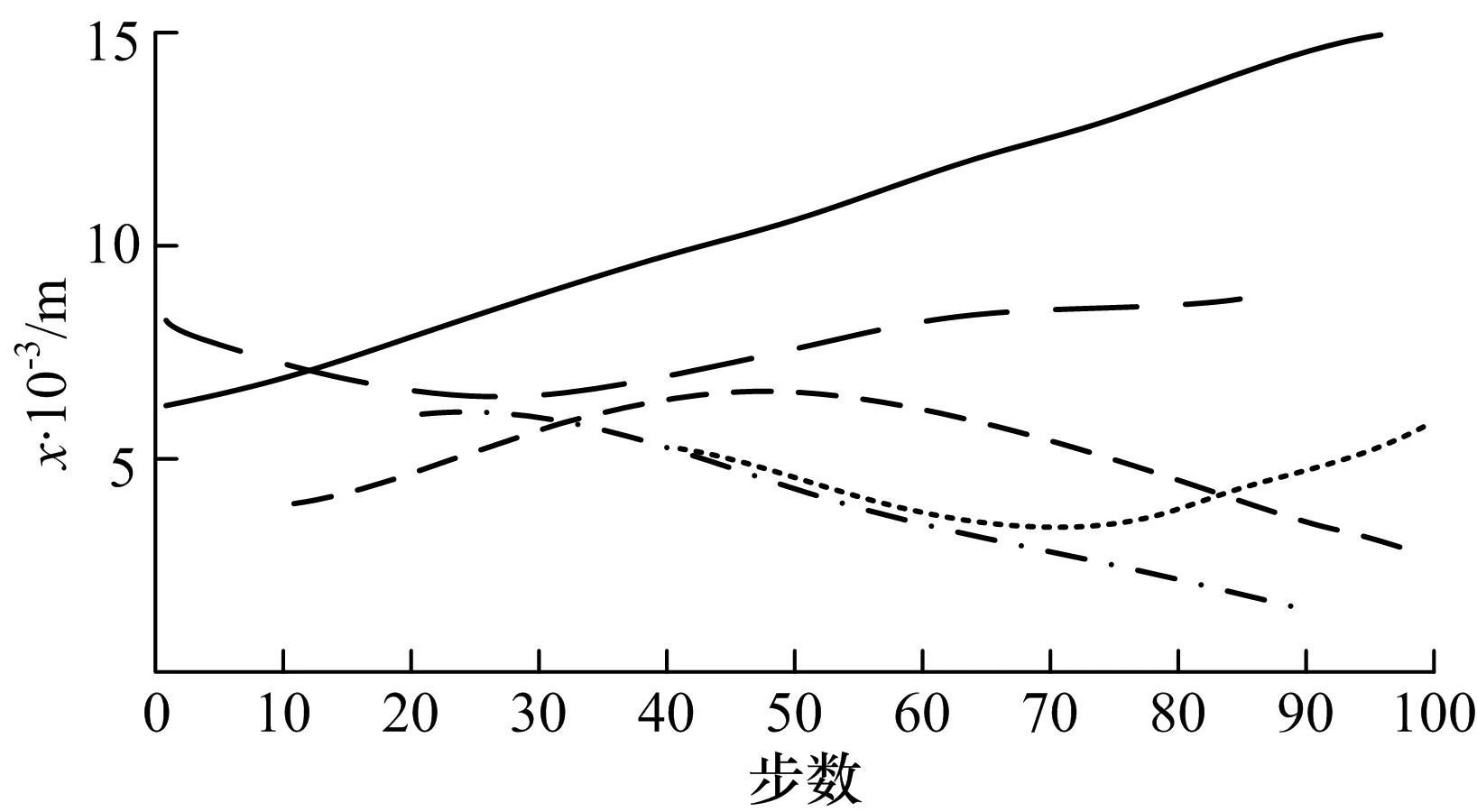
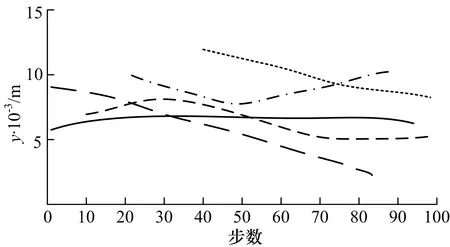
图4 GMSCPHD滤波位置估计

图5 PHD滤波目标数目估计

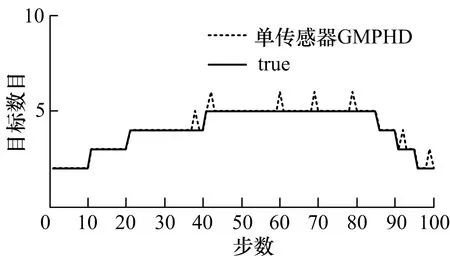
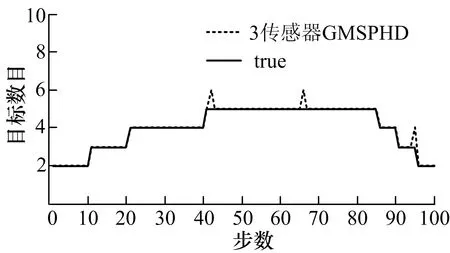
图6 CPHD滤波目标数目估计

图1,2分别为单个传感器的GMPHD滤波算法和GMCPHD滤波算法对多目标的位置估计曲线,图3,4分别为3个传感器的GMSPHD滤波算法和GMSCPHD滤波算法对多目标的位置估计曲线,从图1,4可以看出,3个传感器比单个传感器具有更高的位置估计精度和目标数目估计精度,并且CPHD滤波算法比PHD滤波算法具有更高的多目标跟踪精度．图5为单个传感器PHD滤波算法和3个传感器的序贯PHD滤波算法对目标数目的估计曲线,图6为单个传感器CPHD滤波算法和3个传感器的序贯CPHD滤波算法对目标数目的估计曲线,从图5和图6中可以看出,无论PHD滤波还是CPHD滤波,3个传感器的序贯滤波算法都比单个传感器的滤波算法具有更高的目标数目估计精度,且单个传感器的CPHD滤波算法比3个传感器的序贯PHD滤波算法具有更高的目标数目估计精度,说明CPHD滤波算法对于目标数目的估计效果很好,而3个传感器的序贯CPHD滤波算法对于目标数目的估计精度则更高,说明利用多个传感器的数据进行序贯滤波确实能提高目标估计精度．各算法对于目标数目的估计误差如表1．

表1 各滤波算法对目标数目估计平均误差比较

表2中比较了各算法的平均单次运行时间,从中可以看出CPHD滤波算法比PHD滤波算法的单次平均运行时间有所增加,且传感器数量越多，序贯PHD和序贯CPHD滤波算法的单次平均运行时间越长,原因在于CPHD滤波的计算复杂度为O(NM3)其中N为传感器数量,M为量测集的元素个数,而PHD滤波的计算复杂度为O(NM),又由于传感器数量越多量测数量就越多,序贯CPHD滤波算法比序贯PHD滤波算法计算量增加的幅度要大,单次平均运行时间就越长,但序贯CPHD滤波算法对于目标数目的估计精度要比序贯PHD滤波算法高很多,在满足系统实时性的前提下,文中的多传感器GMSCPHD滤波算法在多目标位置估计和数目估计精度上具有一定的优势．而进行了100步仿真的GMSCPHD滤波算法在2个和3个传感器时的单次平均运行时间分别为22.359 s和25.078 s,每一步的运行时间仅为0.223 59 s和0.250 78 s,相对于10 s的采样周期,还是完全能够保证系统实时性的．

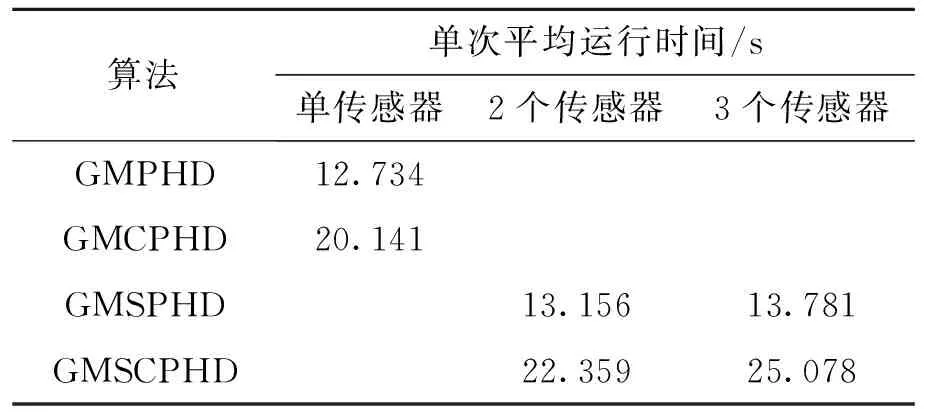
表2 各滤波算法平均单次运行时间比较

3 结论

1) 文中的GMSCPHD滤波算法对多目标数目的估计精度较高,能够有效利用来自多个传感器的量测数据提高目标跟踪精度；

2) 随着传感器数目的增加,系统获得的量测数据增多,GMSCPHD滤波算法的计算量相应增大,但仍然能够满足系统实时性要求,计算量较传统数据关联方法要小很多；

3) 多个传感器监视区域不重叠的情况有可能降低GMSCPHD滤波算法的性能,这一问题将是下一步的研究内容．

[1] Musicki D. Multi-target tracking using multiple passive bearings-only asynchronous sensors[J].IEEETransactionsonAerospaceandElectronicSystems, 2008, 44(3): 1151-1160.

[2] 章飞,孙睿. 基于粒子滤波的多传感器交互式多模型多机动目标跟踪[J]. 江苏科技大学学报:自然科学版, 2011, 25(6): 575-581.

Zhang Fei, Sun Rui. Interacting multiple model tracking algorithm of multiple sensor multiple maneuvering targets based on particle filter[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2011, 25(6): 575-581.(in Chinese)

[3] Alouani A T, Gray J E, McCabe D H. Theory of distributed estimation using multiple asynchronous sensors [J].IEEETransactionsonAerospaceandElectronicSystems, 2005, 41(2): 717-722.

[4] 章飞,孙睿. 基于粒子滤波的水下目标被动跟踪算法[J]. 江苏科技大学学报:自然科学版, 2010, 24(1): 83-87.

Zhang Fei, Sun Rui. Underwater target passive tracking based on particle filter[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2010, 24(1): 83-87.(in Chinese)

[5] Pham N T, Huang W, Ong S H. Multiple sensor multiple object tracking with GMPHD filter[C]∥10thInternationalConferenceonInformationFusion. Quebec QC Canada:[s.n.], 9-12, 2007:1-8.

[6] Mahler R. Multi-target Bayes filtering via first-order multi-target moment[J].IEEETransactionsonAerospaceandElectronicSystems, 2003, 39(4): 1152-1178.

[7] Vo B N, Singh S, Ma W K. Tracking multiple speakers using random sets[C].∥IEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing. Montreal Que Canada：[s.n.],17-21, 2004, II357-II360.

[8] Vo B N, Ma W K. The Gaussian mixture probability hypothesis density filter [J].IEEETransactionsonSignalProcessing, 2006, 54(11): 4091-4104.

[9] Mahler R. PHD filters of higher order in target number[J].IEEETransactionsonAerospaceandElectronicSystems, 2007, 43(4): 1523-1543.

[10] Vo B T, Vo B N, Cantoni A. The cardinalized probability hypothesis density filter for linear Gaussian multi-target models[C]∥IEEEConferenceonInformationSciencesandSystems. Princeton NJ United states:[s.n.] 2006: 681-686.