基于FLUENT的五体船静水中水动力特性数值模拟
2012-11-21陈淑玲杨松林
陈淑玲, 杨松林, 刘 智
(江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212003)
五体船(Pentamaran)是近来发展的一种新船型,其结构由一个主船体和两侧加上4个提供稳性的小侧体组成,静浮时后侧2个浮体有稍许浸沉,前侧2个小浮体的龙骨线位于满载水线之上.国内外已有的理论分析和模型试验结果表明,五体船船型具有高速阻力小,适航性高,稳性较好等优点.文献[1]利用直接计算法对高速五体船结构进行设计,并结合实例阐述了五体船结构设计的外载荷计算、结构分析、疲劳分析等关键问题;文献[2]利用Michell线性兴波理论,以单体船的波谱函数为基础得到了五体船的兴波阻力的计算公式;文献[3]利用高速细长体理论对排水型双体船在波浪上运动性能进行了预报,并可将此理论用到五体船上;文献[4]利用Michell薄船理论,对具有不同纵横向位置侧体的三体船阻力进行了计算,阻力计算结果与试验结果比较接近,可将该理论应用于五体船型的方案优选.作为一种新船型,首要问题之一是快速性,这是评价新船型优劣的基本依据之一.阻力研究途径包括理论计算方法和船模试验研究方法.文献[5]通过试验手段研究了五体船的阻力性能以及五体船后侧体型线形式、位置改变、对称形式、排水量改变、长宽比改变对阻力的影响.文中着重应用数值计算研究方法对五体船型的阻力性能进行系统的研究.
1 控制方程与数值计算方法
1.1 控制方程
对于不可压缩粘性流体,流体遵循质量守恒定律、动量守恒定律和能量守恒定律, 在笛卡尔坐标系下忽略湍流脉动的影响,流体密度为常数,质量守恒及动量守恒方程形式即为连续方程和Navier-Stokes动量方程,其微分形式为:
(1)
(2)
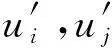
1.2 湍流模型
除了标准k-ω模型[6],FLUENT 6.3及以前的版本还提供了剪切应力输运k-ω模型,简称SSTk-ω模型.如此命名是因为它为了考虑基本的湍动剪切应力而采用了修改过的湍动粘度定义式.因此,它比标准k-ω和标准k-ε模型有更好地表现.其它的修正(包括ω输运方程中的交叉扩散项以及混合函数)则是为了保证该模型在近壁区域和远场都有很好的预测效果.和高雷诺数湍流模型相比,它消耗的计算时间少.文中应用的SSTk-ω湍流模型的方程如下:
(3)

(4)
式中:Gk是由于平均速度梯度引起的湍动能k的产生项,Gω是由ω方程的产生项,它们的表达式都和标准k-ω模型中的一致;Γk和Γω表明了k和ω的有效扩散;Yk和Yω是由湍动产生的耗散,它的表达式和标准k-ω模型中的相同;Dω为交叉扩散项;Sk和Sω是用户自定义的源项.
1.3 自由面处理方法
在FLUENT中,采用VOF模型用于处理自由液面问题.VOF方法是基于两种或多种流体(或相)互相之间没有穿插这一事实.对于包含空气和水两相流体的空间区域,定义标量函数f,存在水空间点的f值等于1,其他不被水占据点的f值为0.在各网格单元上对f值积分,并把这一积分值除以单元体积, 得到单元的f平均值,即网格单元中水所占据的单元体积份额,在VOF方法中把这一份额值定义为F.若在某时刻网格单元中F=1,说明该单元全部为指定相水所占据,为水单元;若F=0,则该单元全部为空气所占据.当0 (5) 文中五体船的主体和附体都是采用的Wigley船型建立的模型.Wigley船型作为含自由面船模绕流场CFD具体研究的第一个对象,是因为它有相对比较简单的几何船型,已被广泛研究并获得了一定数量的资料积累[7-9]. Wigley船型的几何表达由下面的方程式给出: (6) 式中:B是船宽,L是船长,H是船的吃水深度,0≤x≤L,-H≤Z≤0.Wigley船型的主要参数列于表1,其中LPP是垂线间长,CB是方形系数. 表1Wigley船型主要参数 Table1Principledimensionofthewigleyhull. B/LPPH/LPPL/LPPCB0.10.62510.44 文中计算对象为小水线面五体船船型.主船体水线长1 m,水线面宽0.1 m.前后端附体长0.21 m,宽0.02 m.前后附体中线与主体中线距离相同.船模主体在静水情况下吃水为0.1 m,后端附体吃水0.06 m,前端附体在水线以上0.01 m.五体船模型如图1. 图1 五体船模型外形俯视图 为尽量消除边界反射的影响,经过多次计算实践并参考相关文献[10-12], 采用的控制域为一长方体, 并按如下方案设置计算控制域的范围及船模在控制域中的位置:船首前端计算区域取1倍船长,船尾后为3倍船长,船底以下计算区域为15倍吃水,甲板以上计算区域为4倍吃水,宽度方向为10倍附体与主体间距.主船体船长为1 m, 得到计算控制域的长、宽、高分别为5,1,1.3 m.模型关于中纵剖面对称,取一半进行计算即可.为简化建模过程,将坐标原点设置在船尾最低点,x轴取指向船首为正,y轴取指向右舷为正,z轴取向上为正.船模在控制域中的位置及控制体情况如图2. 图2 计算流场区域 a) 船体表面网格图 b) 计算域网格图 文中的五体船结构复杂,因此使用单块结构化网格已不能获得较高网格质量的计算网格,为此,采用多块结构化网格,整个计算区域共分77块,在参考作者以前所做的网格收敛性的研究和有关文献资料的基础上,网格单元总数取为560 950.为了模拟边界层内流动,网格在靠近物体表面处加密.图3为计算区域的网格划分图. 计算区域的边界包括:入口边界、出口边界、船体(含主船体和侧片体)、计算域侧边界和上下边界(包含顶部和底部).① 进口边界条件,在计算域的进口处,给定速度为船模航行速度;② 出口边界条件,使用压力出口边界条件,即出口处的水压随水深成线性增加p=ρgh(其中:ρ水的密度,g重力加速度,h水的高度);③ 壁面边界条件,在船体表面上满足无滑移条件;④ 对称面边界条件,在对称面上满足对称面条件. 船模航行速度V=2 m/s,对应的傅汝德数为0.7. 选用计算流体力学软件FLUENT作为求解器,使用有限体积法(finite volume method, FVM)对控制方程进行离散,其中对流项采用二阶迎风差分格式,扩散项采用中心差分格式.离散得到的差分方程组具有高度耦合性和非线性,使用 SIMPLE(semi-implicit method for pressure linked equations) 方法求解,时间步长为0.005. 计算了3种不同附体与主体间距的五体船船型,3种间距(a)分别为0.08,0.10,0.12 m.通过计算得到了各船型在同一航速下的兴波状况和水的总阻力系数Cd等参数.其中: (7) 式中:Rt为船舶总阻力,ρ为水的密度,v为从船舶航速,S为船体湿面积. 表2为船舶同一航速下不同附体和主体中心距的五体船总阻力系数,可以发现,在附体与主体中心距为0.10 m时达到最大值,0.12 m时船体的总阻力最小,0.08 m其次. 表2同一航速下,附体与主体不同中心距五体船的总阻力系数 Table2Totalresistancecoefficientofpentamaranwithdifferentdistancebetweenmainhullandside-hull a/m0.080.10.12 Cd0.005 3550.005 7970.005 216 a) a=0.08 m b) a=0.10 m c) a=0.12 m 图5分别为附体与主体中心距分别为0.08,0.10,0.12 m时船兴波的波形图.由船舶阻力理论[12]可知,船舶总阻力由粘性阻力和兴波阻力组成,粘性阻力主要和雷诺数Re相关,当来流速度相等,雷诺数相同,船舶的粘性阻力系数相等.兴波的波高反应了船体兴波阻力的大小,兴起的波浪越高船体损失的能量越多,船舶兴波阻力就越大.该五体船的水线为-0.068 42,从图中可以看出a=0.12 m时兴波的波高最低,所以a=0.12 m时兴波阻力最小,总阻力最小,这和图4曲线的结果相一致.同时通过观察波形图可以看到附体所在位置对主船体阻力的影响,图6b)中,首部两个附体增加了主船体首部的兴波,船尾部的两个附体也增加了波谷的值,因此造成了船舶主体兴波阻力的不利干扰,使总阻力增加,和图4曲线的结果也一致. a) a=0.08 m b) a=0.10 m c) a=0.12 m 图6中给出了Fr=0.7时附体与主体中心距a=0.08,0.10,0.12 m 3种情况下阻力系数Cd时间历程变化曲线,通过图7可以发现计算结果均已收敛,中心距的增加将导致计算收敛速度变慢.因为附体距主体之间的中心距划分的网格数相同,随着中心距的增加网格尺寸变大,网格尺寸的变化导致了收敛速度变慢. a) a=0.08 m b) a=0.10 m c) a=0.12 m 利用RANS 方程、SSTk-ω湍流模型和模拟自由面的VOF方法对水面高速五体船的水动力特性进行计算, 通过结果分析表明文中建立的模型是可靠的.计算研究表明,五体船的阻力特性和附体横向位置有关,在附体与主体中心距为0.12 m时船体的总阻力最小;通过对水下船体表面的压力分布进一步分析了船体粘压阻力的形成及附体对粘压阻力的影响;通过对自由水线面形状的分析可知,文中附体的位置对主体兴波阻力并没造成有利干扰,因此以后可以通过调整附体与主体之间的纵向距离对五体船的阻力特性进行进一步的研究.同时附体与主体横向间距的增加将导致计算收敛速度变慢. [1] 卢晨,肖熙. 高速五体船结构设计的几个关键问题[J].船舶,2004, 10(5):21-26. Lu Chen, Xiao Xi. Key problems in designing the structures of the high speed pentamaran[J].Ship&Boat, 2004, 10(5):21-26.(in Chinese) [2] 蔡新功,常赫斌,王平.多体船型在静水中的兴波阻力研究[J].水动力学研究与进展,2009,24(6):713-723. Cai Xingong, Chang Hebin, Wang Ping. Research about the wave-making resistance of multi-hull ship in the calm water[J].ChineseJournalofHydrodynamics, 2009, 24(6):713-723.(in Chinese) [3] 段文洋,贺五洲. 高速细长体理论在双体船运动计算中的应用[J].工程力学, 2002, 19(2):138-142. Duan Wenyang, He Wuzhou. Application of the high-speed slender body theory to motion estimation for catamarans[J].EngineeringMechanics, 2002, 19(2):138-142.(in Chinese) [4] 蔡新功,王平,谢小敏. 三体船方案优化布局的阻力计算与试验研究[J]. 水动力学研究与进展,2007, 22(2):202-207. Cai Xingong, Wang Ping, Xie Xiaomin. Resistance study on alterative layouts of the trimaran hull configuration[J].JournalofHydrodynamics, 2007, 22(2):202-207.(in Chinese) [5] 贺俊松,张凤香,陈震. 五体船型的阻力性能试验[J]. 上海交通大学学报,2007, 41(9):1449-1453. He Junsong, Zhang Fengxiang, Chen Zhen. An experimental study on pentamaran resistance characteristics[J].JournalofShanghaiJiaotongUniversity, 2007, 41(9):1449-1453.(in Chinese) [6] 王瑞金,张凯,王刚. Fluent技术基础与应用实例[M]. 北京:清华大学出版社,2007:113-143. [7] Fuat Kara, Chun Quan Tang, Dracos Vassalos. Time domain three-dimensional fully nonlinear computations of steady body-wave interaction problem[J].OceanEngineering, 2007, 34:773-789. [8] Celebi M S. Computation of transient nonlinear ship waves using an adaptive algorithm[J].JournalofFluidsandStructures, 2000,14:281-301. [9] Wang Q X. Unstructured MEL modelling of nonlinear unsteady ship waves[J].JournalofComputationalPhysics, 2005, 210:368-385. [10] 张志荣, 赵峰, 李百齐. 绕船体粘性自由面流动的数值计算(英文)[J]. 船舶力学, 2002, 6(6):10-17. Zhang Zhirong, Zhao Feng, Li Baiqi. Numerical simulation of three-dimensional viscous flow with free surface about a ship[J].JournalofShipMechanics, 2002, 6(6):10-17.(in Chinese) [11] 李良彦.船舶阻力及粘性流场的数值模拟[D]. 大连:大连理工大学,2008. [12] 盛振邦,刘应中.船舶原理[M]. 上海: 上海交通大学出版社,2003:189-210.2 数值计算
2.1 计算模型

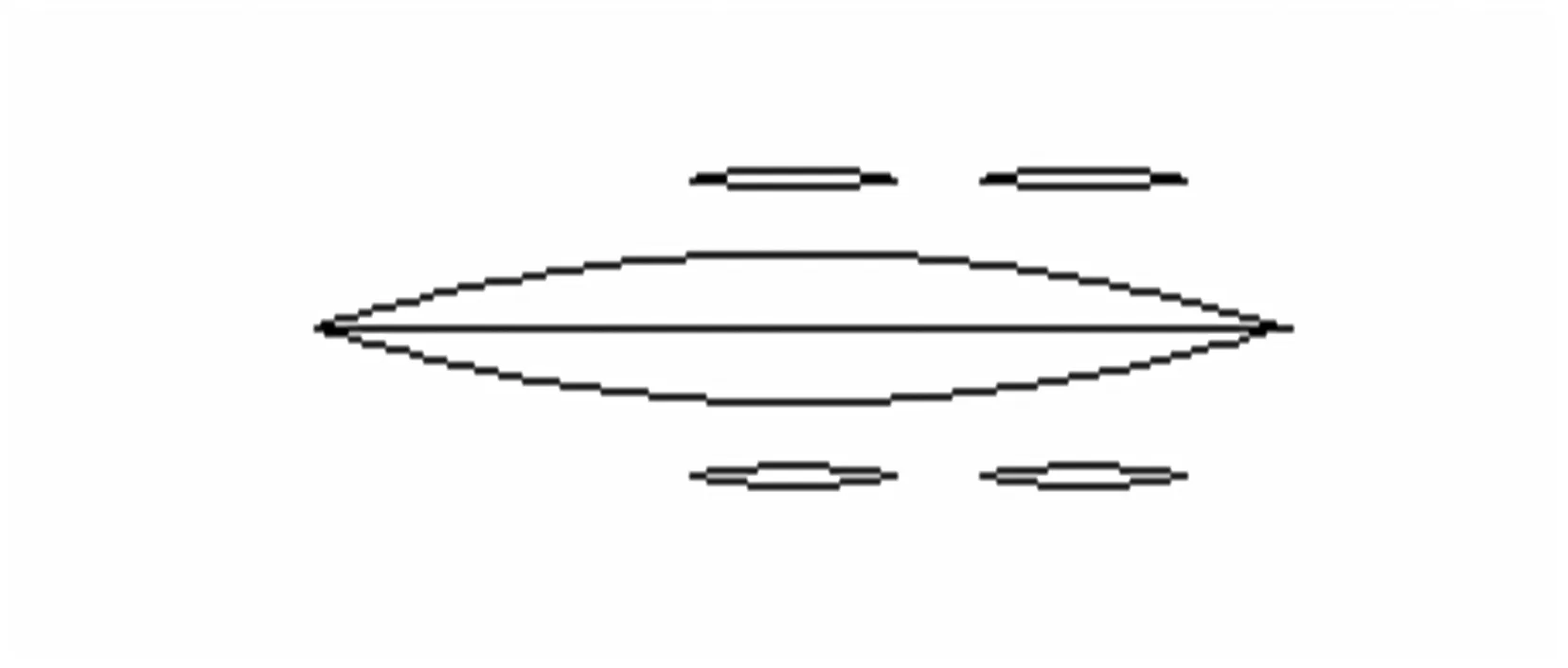
2.2 计算区域及网格划分



2.3 边界条件
2.4 数值方法
3 数值模拟结果及分析

3.1 船体表面压力分布



3.2 自由水面线形状



3.3 间距对收敛速度的影响



4 结论
