平面解析几何中的坐标转换及应用

陈 英 杨 华 赵浩彦

(北京林业大学 省部共建森林培育与保护教育部重点实验室，北京 100083)

在平面解析几何中，有直角坐标的平移和旋转，还有极坐标与直角坐标之间的相互转换。直角坐标系中，坐标的平移，讲究的是一个相对坐标和绝对坐标。坐标的平移，是由坐标轴的平移和转动造成的。如果能弄清楚原坐标的移动距离、移动方向、转过的角度(相对于原坐标移动之前)，那么所要求的坐标，也做原坐标同样的变换就可以在新坐标中找到对应的位置。以下笔者就坐标旋转来讨论新坐标在原坐标中的位置。

1 坐标换算原理

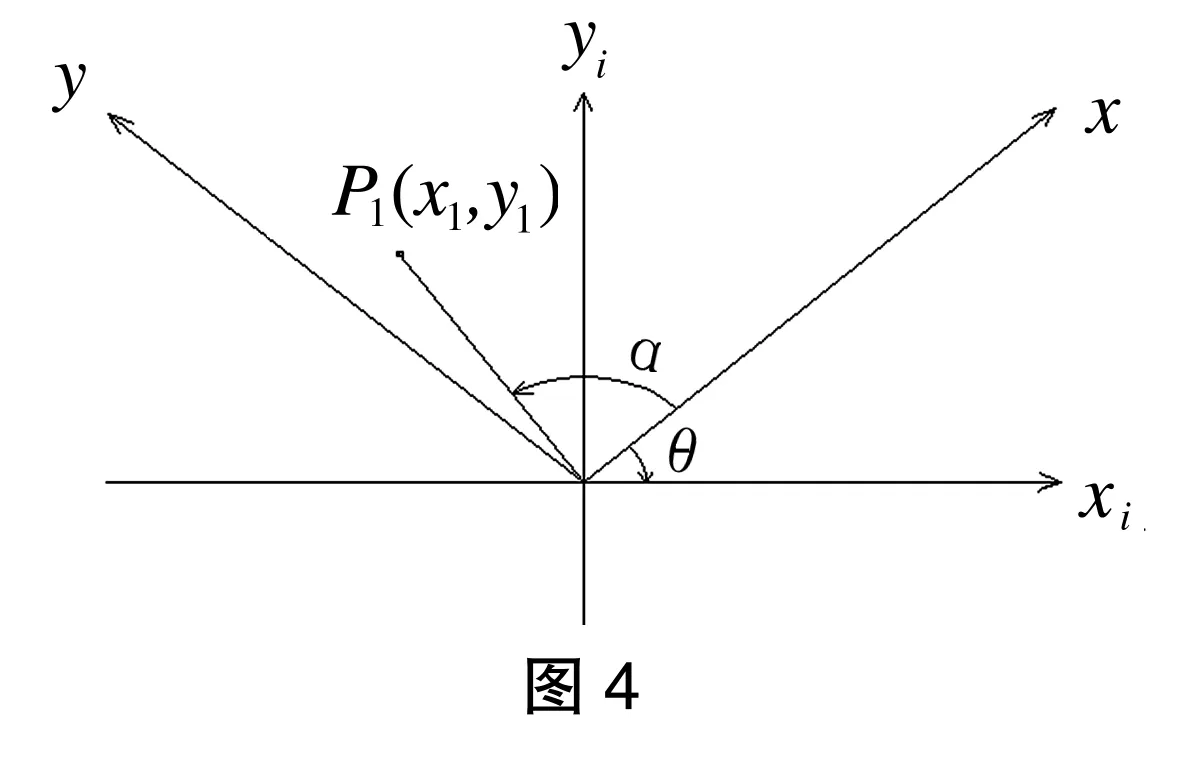
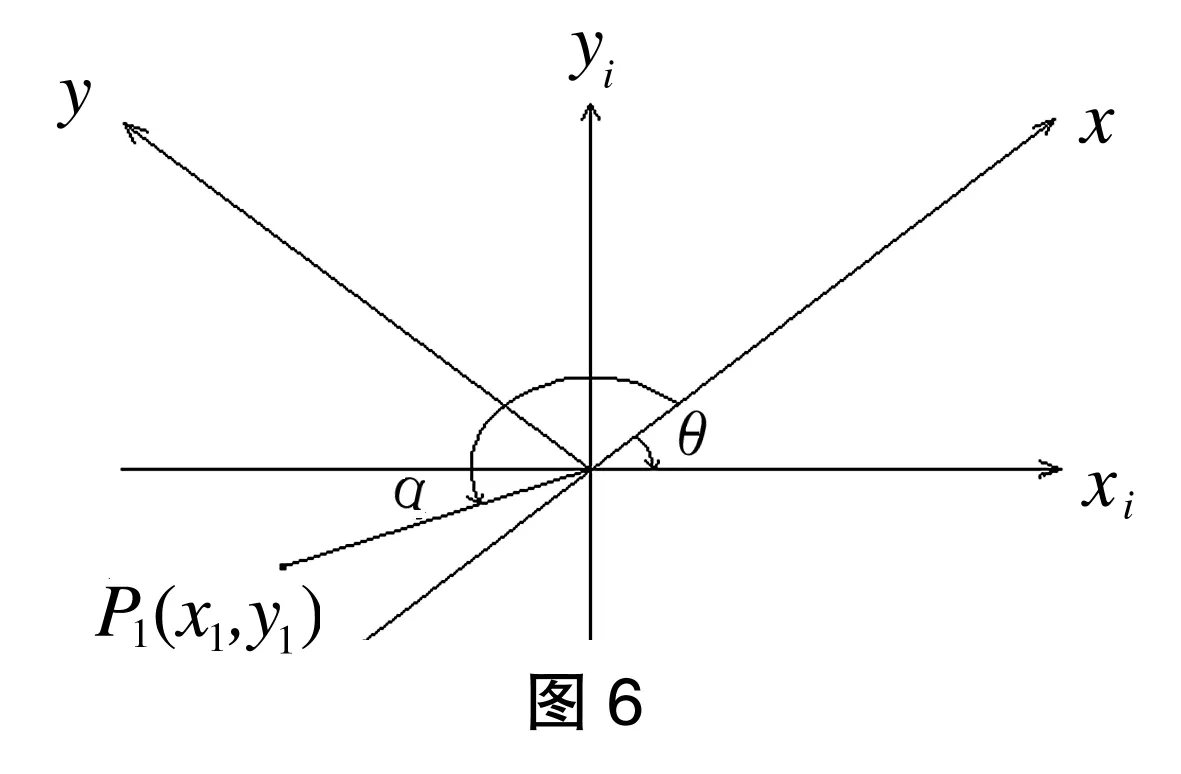
假设旋转前的坐标为X、Y，旋转后的坐标为Xi、Yi，坐标原点均为O，旋转角度为θ(如图1所示)，原坐标系中存在一点P(x、y)，经过θ角度的旋转后，P点在新坐标系中的坐标值P1(x1、y1)能用相应的换算公式计算出来。而P点与现坐标轴Xi之间的角度为α。

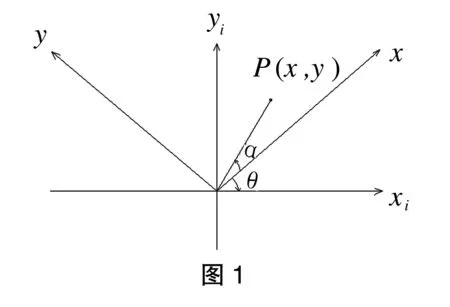
由于原坐标所在新坐标的象限有所不同，故可以导致x1、y1的换算公式不同，下面我们分象限依次讨论：

1.1 原坐标Y在新坐标的第二象限

1.1.1 点P1在第一象限，且界于X与Yi之间(如图2所示)

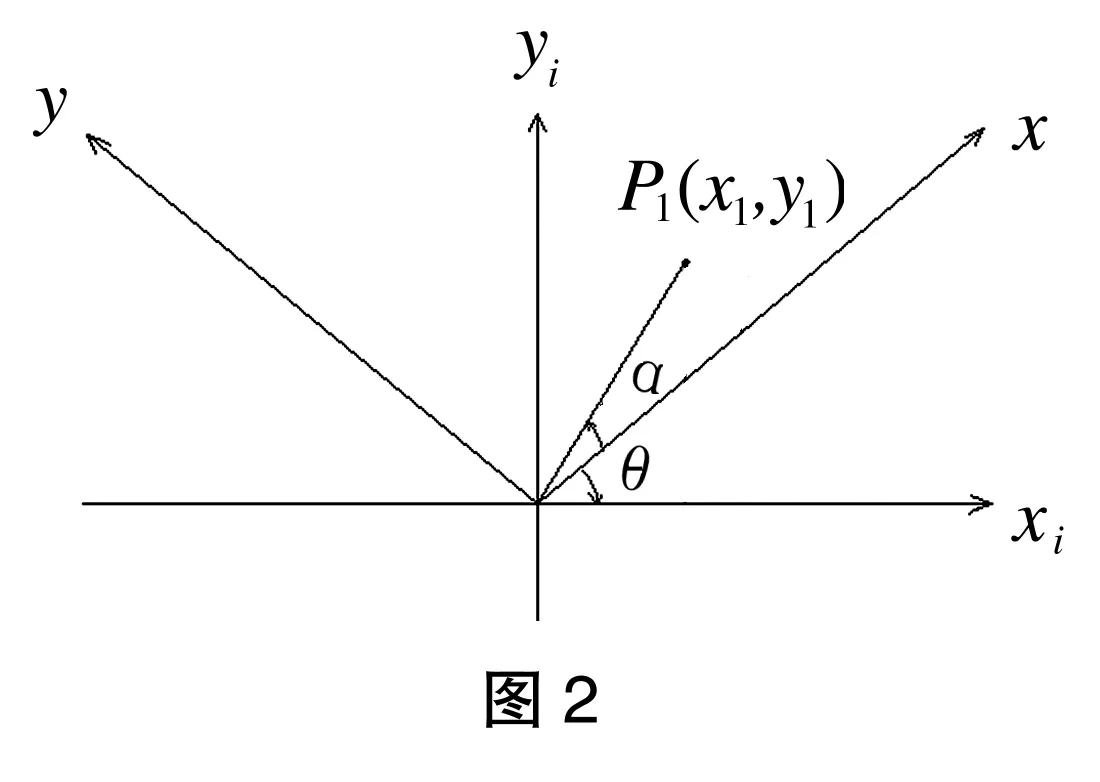
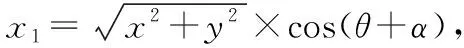
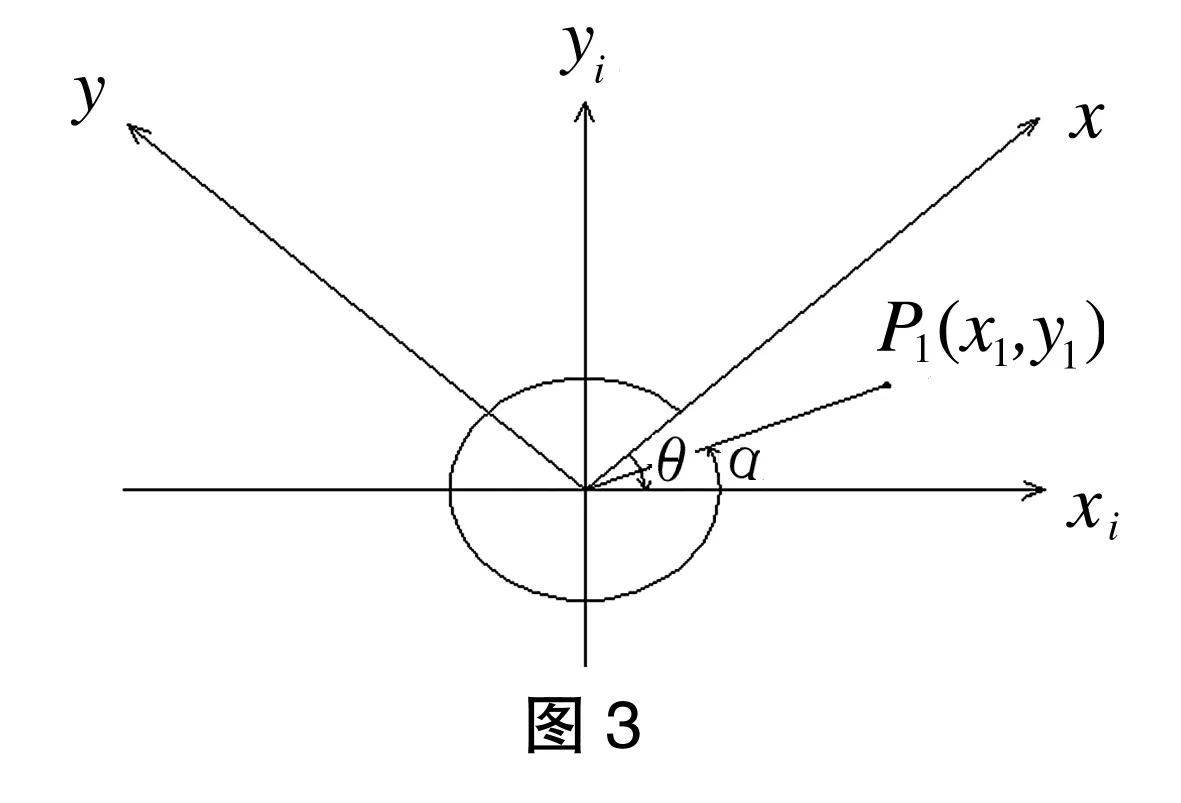
1.1.2 点P1在第一象限，且界于X与Xi之间(如图3所示)

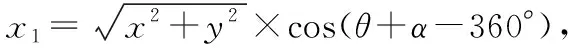
1.1.3 点P1在第二象限，且界于Y与Yi之间(如图4所示)

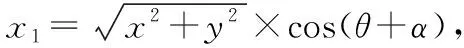
1.1.4 点P1在第二象限，且界于Xi与Y之间(如图5所示)

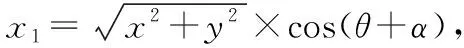
1.1.5 点P1在第三象限，且界于X与Xi之间(如图6所示)

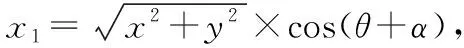
1.1.6 点P1在第三象限，且界于X与Yi之间(如图7所示)

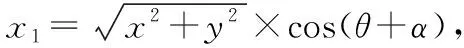
1.1.7 点P1在第四象限，且界于Y与Yi之间(如图8所示)

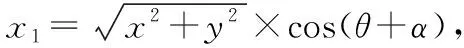
1.1.8 点P1在第四象限，且界于Y与Xi之间(如图8所示)

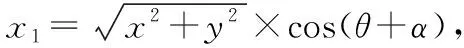
由以上结果可知：原坐标Y在新坐标的第二象限时，新坐标系中的坐标值P1(x1、y1)相应的换算公式有(1)和(2)两种：

按照相同的方法，我们能得出X、Y在其他象限时候，P1(x1、y1)相应的换算公式。

1.2 原坐标Y别在新坐标的第一象限时，换算公式有(3)和(4)两种

1.3 原坐标Y在新坐标的第四象限时，换算公式有(5)和(6)两种

1.4 原坐标Y在新坐标的第三象限时，换算公式有(7)和(8)两种

2 总结

由以上(1)-(8)换算公式可知，无论怎么旋转，旋转后的新坐标所对应的换算公式都只有(Ⅰ)和(Ⅱ)两种：

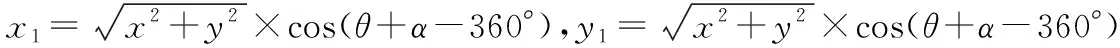
根据三角函数公式sin(2kπ+δ)=sinδ,cos(2kπ+δ)=cosδ和sin(-δ)=-sinδ，cos(-δ)=cosδ[1]可知：公式(Ⅰ)和(Ⅱ)相等，即：

由此可知，平面直角坐标系中，存在一点P(x、y)，无论经过什么角度旋转，P点在新坐标系中的坐标值P1(x1、y1)都可以表示为：

3 坐标换算的应用

假设林业做标准地调查时，以正北方向为原坐标的Y轴方向，应用全站仪将样地里的每棵树都定位，后将全站仪顺时针旋转45°后，即原坐标Y在新坐标的第二象限时，应用上述计算公式可得到原来每棵树相应的新坐标，表1为原坐标中树木点坐标转换后的换算情况。

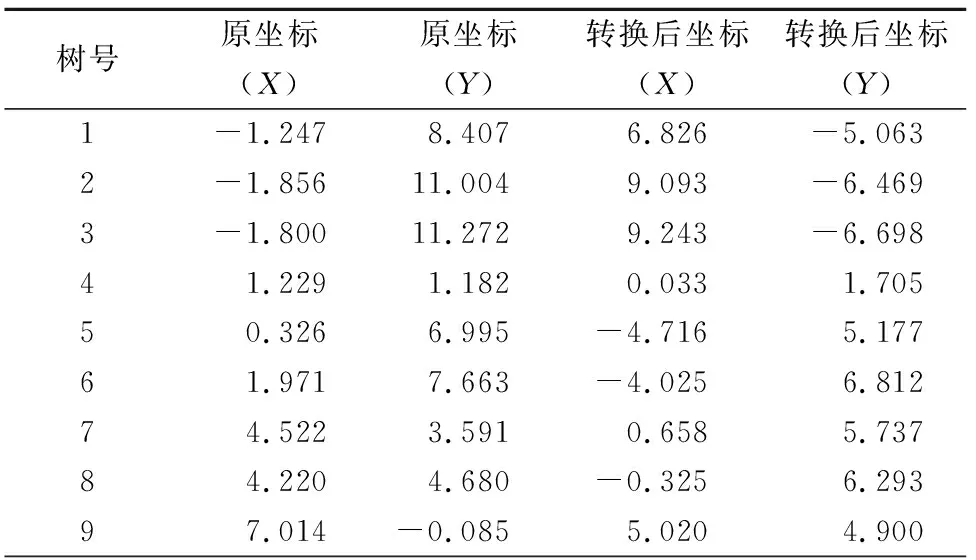
表1 树木点坐标旋转后换算情况

续表

树号原坐标(X)原坐标(Y)转换后坐标(X)转换后坐标(Y)106.9040.1554.7724.991116.9020.4244.5815.180126.481-0.6755.0604.105135.829-1.6155.2642.980148.433-3.8358.6753.251155.613-5.8048.073-0.135

4 结论

本文推导的计算公式可用一般的函数计算器计算，其运算过程直观、明了，具有较强的实用性和可操作性，适用于野外作业[2]。

参考文献：

[1]虞涛.高中课本中的数学基本解题方法(上册)[M].上海：华东师范大学出版社,2008.

[2]李明贵.最小二乘法在平面直角坐标换算中的应用[J].四川林勘设计,2009,9(3):83～85.