深度关注过程 积累活动经验

饶道松

（南京师范大学附中仙林学校小学部，江苏 南京 210046）

2011年版的《数学课程标准》把基本活动经验作为“四基”之一提出来，并进一步明确了获得数学活动经验也是数学课程目标的核心和主干之一。这就要求我们教师重视学生数学活动经验的积累，而积累基本的数学活动经验需要学生有足够的时间和空间，以经历观察、实验、猜测、计算、推理、验证等活动过程。课堂是学生积累数学活动经验的主阵地。在课堂教学中，让学生经历什么样的数学活动过程，学生就有可能积累什么样的数学活动经验。从这个意义上来说，课前精心设计好数学活动，课中以学生为主体，充分经历活动过程就显得尤为重要。笔者认为，在教学中，需要深度关注学生的动手操作、实践探究、数学思维和设疑解疑等四个方面的活动，帮助学生逐步积累数学活动经验。

一、关注学生动手操作活动

案例1.《认识长方形和正方形》

师：同学们，请你用数学的眼睛来观察我们教室中物体的面，你能找出你认识的面吗？

生：有长方形、圆、平行四边形、正方形、三角形……（随孩子的回答抽象出这些平面图形）

……

师：在你眼里，长方形、正方形到底具有怎样的特点呢？（4人小组交流后写在作业纸上）

生1：长方形有四个直角。

生2：长方形还有四条边，一条长一些，一条短一些！

生3：正方形也有四个直角。生4：正方形的四条边都是相等的。

师：同学们的这些猜想是不是正确呢？我们得验证吧！大家可以利用大信封中里的材料（长方形和正方形的纸片、直尺、三角尺等）来证明你的猜想或者补充你的发现。（学生分组进行操作活动，活动后学生各小组汇报）

师：好的，我们现在回顾一下，刚才是如何展开研究的？

生1：我们先猜想了图形有哪些特征再动手操作验证。

生2：我们首先发现要从边和角两个角度对两个图形展开研究，我认为观察图形的角度很重要。

生3：我们还采用了数一数、量一量、比一比、折一折的办法，所以验证图形可以有多种办法。

案例中结合学生已有的生活经验，让学生观察教室中物体的面，抽象出相关的平面图形，直观感悟长方形和正方形的特点，这只是对长方形和正方形的感性认识。它们到底有什么特点呢？让孩子们通过数一数、量一量、比一比、折一折等具体的动手实践操作活动来理解长方形和正方形的特点，上升到对长方形和正方形的理性认识。如果从“双基”的培养来说，到这层就可以了，但是案例中的活动并没有停止而是教师继续问道：我们又是如何展开研究的？学生在这样的回顾活动中不仅加深了对长方形和正方形特点的理解，还能引导学生从归纳总结中汇总并逐步积累具体的行为操作经验。

二、关注学生实践探究活动

案例2.苏教版五上P63《解决问题的策略》片段

课件出示：王大叔用18根1米长的木桩围成一个长方形羊圈，有多少种不同的围法？

师：王大叔可以怎么围呢？同桌2人相互合作，把你想到的围法都记下来，等会儿交流。（学生进行操作，接着汇报交流）

生：第一种长8米，宽1米；第二种长7米，宽2米；第三种长6米，宽3米；第四种长5米，宽4米，一共有四种围法。

师：你是怎么想的？

生：因为9=8+1=7+2=6+3=5+4，所以一共有4种。

师：那这里的9是什么意思呢？

生：18根1米长的木桩围成一个长方形周长就是18米，长与宽的和就是18÷2=9米。

生：还可以利用表格的形式，展示。

长（m） 8 7 6 5宽（m） 1 2 3 4

师：如果你是王大叔，你会选择哪种围法？说说你的理由。

生：我会选第四种，长5米，宽4米的羊圈。这种围法面积最大，养的羊最多。

师：是这样吗？让我们一起来计算一下它们的面积。（师相机点击课件）

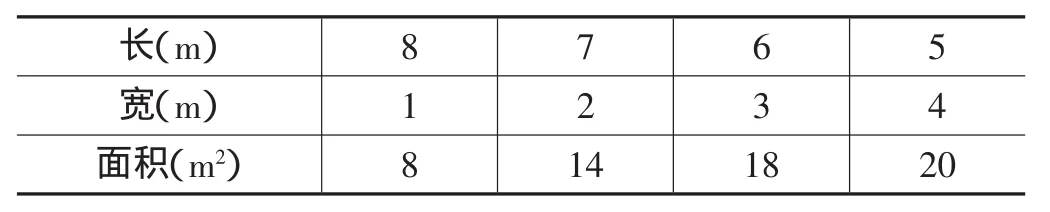
长（m） 8 7 6 5宽（m） 1 2 3 4面积（m2） 8 14 18 20

师：哦，有意思。这四个长方形的周长——（生：相等），但它们的面积却不相等。那让我们仔细观察、比较一下这四个长方形的长、宽、周长、面积，从中你发现了什么？（学生独立探究，再小组交流）

生：我发现了长方形的周长相等，长越长，宽越短，面积就越小。

师：长越长，宽越短可以说成长、宽的差——（生：越大）还有谁要说？

生：长与宽的差越大，面积就越小；长与宽的差越小，面积就越大。

师：是啊，长方形的周长相等，长与宽的差越小，面积就越大。相信王大叔一定会采取大家的意见的。通过这个例题的学习，你明白了什么？

生1：我学会了采用一一列举的办法来帮助我全面而准确的找到答案。

生2：我不仅学会了解题的方法，还有意外的收获——找到了隐藏的规律。

实践探究就是围绕一个数学问题进行动手操作活动，在操作活动基础上进行理性的思维活动。在此案例中，首先抛出“围成长方形羊圈有多少种不同的围法？”这个问题让学生进行具体操作，得出共有4种不同的围法并引导学生按照一定顺序填写表格，帮助学生获得一一列举的经验。此外，通过计算得到围成羊圈的最大面积，再进行观察、比较、分析、概括得出“长方形的周长相等，长与宽的差越大，面积就越小；长与宽的差越小，面积就越大的规律”。如此，学生实践探究活动经验化无形为有形，便于学生积累。

三、关注学生数学思维活动

案例3.苏教版四下P54《乘法分配律》片段

板书：（65+45）×5=65×5+45×5，（32+45）×3=32×3+45×3

师：请同学们仔细观察这两个等式左右两边，根据它们的特点写出（15+23）×4=的右边部分。

生：（15+23）×4=15×4+23×4。

师：像这样你还能写出几个吗？

生：（123+54）×32=123×32+54×32。

师：除了用数表示这样的特点以外，你还能用其他形式表示吗？

生 1：（数+学）×书=数×书+学×书。

生 2：（◇+□）×△=◇×△+□×△。

生 3：（a+b）×c=a×c+b×c。

师：像这样的特点，你能用一句话来描述吗？（同桌相互说一说）

生：两个数的和与一个数相乘等于这两个数分别与这个数相乘，再相加。

我们认为不借助于直观材料进行的数学活动而获得的经验就是数学思维活动经验。在此案例中，教师首先让学生通过观察、比较、分析初步感悟乘法分配律的特点；二是让学生结合感悟有层次地模仿写2组这样特点的等式；三是通过分析、类比、推理，让学生用不同的形式（如：文字表示、几何图形表示、字母表示等）写出等式来；四是根据对乘法分配律的理解进行概括、总结，用一句话来描述乘法分配律的含义。小学生的数学思维活动主要包括归纳、数据分析、类比、对比、推理等等活动。学生在教师的引导下经历了一系列的数学思维活动，为有效的积累数学思维活动经验提供可能，也为学生进行创新性活动奠定基础。

四、关注学生设疑解疑活动

案例4.苏教版五上P50练习八第3题

师：你还能提出什么问题？该如何列式呢？

生1：小冬从家到少年宫比从家到学校要远多少千米？（2.15-0.55）

生2：小冬家离少年宫的距离比小华家离少年宫的距离近多少千米？（0.55+1.55）

生3：小华从学校回家的距离和他从学校到少年宫的距离相差多远？（2.15+0.55-1.55）。

设疑解疑活动指的就是学生发现和提出问题，进而分析和解决问题。在案例中，教师在提出“你还能提出什么问题”之前，教科书已经预设了3个问题，所以再提出有价值性的问题必须先深刻分析给出的条件，然后发现问题，再提出问题，最后分析问题、解决问题。比如：生2提出的这个问题其实就是小冬和小华两家之间的距离；生3提出小华从校到家的距离和从校到少年宫的距离相差多远。这两个问题的提出都非常有水准，需要大动脑筋思考，这与跟着教师去验证、推断既有的结论是不同的思维方式。课堂教学中，教师有意识创设多种情境，让学生多进行这样的活动，积累设疑解疑的活动经验，以达到促进学生逐步形成创新能力的目的。

《数学课程标准》特别指出：数学活动经验的积累是提高学生素养的重要标志，帮助学生积累数学活动经验是数学教学的重要目标。一线的教师应该更加关注课堂教学的活动设计，更加重视学生经历知识的形成过程，更加重视过程与结果的和谐统一，让学生积累更多能够“带得走的东西”——基本的数学活动经验。

[1]王林.小学数学课程标准研究与实践 [M].江苏教育出版社，2011.