台阶式溢洪道非掺气水流水面线的计算

张志昌，徐 啸

(西安理工大学，陕西 西安 710048)

台阶式溢洪道水面线的计算是确定溢洪道高度的重要问题.由于台阶的特殊构造，使得台阶上水面线的计算比光滑溢洪道更加复杂.目前，尚无系统、成熟的台阶式溢洪道水面线的研究成果.

文献［1］曾采用紊流边界层理论计算台阶式溢洪道水面线，但计算结果与实测相差甚远.文献［2］通过试验研究了坡度为51.3°和60°台阶式溢洪道上的水面线分布规律，得出台阶式溢洪道上水深的计算公式，但该方法没有将非掺气水深和掺气水深区别开来.S.L.Hunt等［3］对3种不同角度(15°，30°和52°)的台阶式溢洪道进行了模型试验，模型台阶高度为1.4 cm，最大单宽流量为0.347 m2/s，试验得出当不考虑掺气影响、溢洪道坡度为15°时，最大水深正好等于临界水深hk，而当坡度为30°和52°时，最大水深分别为1.75hk和3.0hk.文献［4］提出了1个台阶式溢洪道上水深计算的复杂公式，该公式仍然未将非掺气水深和掺气水深分开计算，计算误差有的在10%以内，有的超过10% ～15%.文献［5］根据文献［6－7］的试验，认为坡度一定的台阶式溢洪道上的滑行水流，在经过几级台阶后，即变为正常水深的均匀流，探讨了形成均匀流的条件.事实上，只有在单宽流量较小时，才会在几级台阶之后形成均匀流，而当单宽流量较大时，在台阶式溢洪道上形成均匀流尚需一定的距离.文献［8］研究了台阶式溢洪道上准均匀流(即均匀掺气水流段)的条件，得出准均匀流段正常水深的计算公式.但未涉及准均匀流段以前的水深计算.文献［9］根据明渠非均匀渐变流理论，推导了台阶坝面滑行水流水深的计算公式为

式中:动能修正系数取α1=1.7～2.0;λ为沿程阻力系数，可根据蔡克士大明槽沿程阻力系数的公式计算;h1为已知断面水深;h2为计算断面水深;q为单宽流量;Δl为计算流段长度;i为溢洪道坡度;g为重力加速度.在计算λ时，首先按照ksu*/ν(u*为摩阻流速，ν为黏滞系数)判断水流流态所属区域，即光滑区、过渡区还是粗糙区，选择不同公式求出λ，再代回式(1)求得水深h2.该式没有给出动能修正系数α1等于1.7～2.0的依据，也没有考虑坡度θ对水深的影响，这对于坡度较大的台阶式溢洪道水面线的计算将会引起较大的误差.

台阶式溢洪道由于底部的特殊构造，在台阶的虚拟底板以上形成滑行水流，在虚拟底板以下的台阶内形成水流旋滚，水流流态十分复杂.水流在流动过程中不仅有沿程水头损失，而且台阶内的水流旋滚造成了台阶上的局部水头损失.所以，在台阶式溢洪道水深的计算中，必须考虑局部水头损失的影响.但目前尚无台阶上局部阻力系数的研究成果.

本文根据明渠非均匀渐变流理论，通过分析和试验对比，确定台阶式溢洪道上的局部阻力系数;根据动量方程，推导反弧段水面线的计算公式;通过试验，给出台阶式溢洪道上游WES曲线段水面线的计算方法.

1 试验模型

台阶式溢洪道由WES曲线段、光滑直线段、台阶段和反弧段组成.台阶的高度为 5 cm，试验的坡度分别为 30°，51.3°和60°，坡度为30°时，模型高度为186.63 cm，台阶数为30 级，坡度为51.3°和60°时模型高度均为203 cm，台阶数为33级和32级.堰上定型设计水头 Hd=20 cm，模型单宽流量的范围为0.058 5 ～0.350 2 m2/s，堰上流能比0.681，H为堰上水头，q为单宽流量.模型布置见图1.

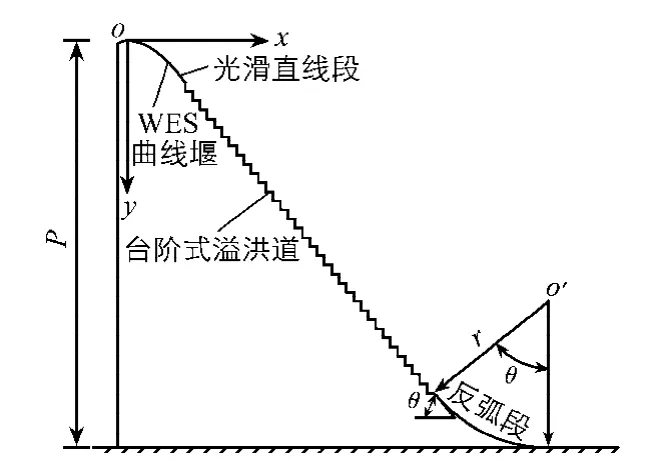
图1 试验模型Fig.1 Sketch of experiment model

2 台阶式溢洪道水面曲线的计算

2.1 堰面曲线段

堰面曲线段的水面线计算一般是查水工设计手册第六分册表27－2－3.但该表格查算的范围有限，往往不能满足设计要求.本文根据模型试验测得溢洪道坡度为30°，51.3°和60°的堰面曲线段水深，其中坡度为60°的相对水深与相对距离的关系如图2所示，图中x切为切点距堰顶的水平距离，x为测点距堰顶的水平距离，h为垂直于堰面的水深，Hd为堰上设计水头.对于坡度为30°和51.3°，亦有与图2相同的规律.由图可得水深的计算公式为

图2 h/Hd与x/x切的关系(坡度为60°)Fig.2 Relationship between h/Hdand x/x切(slope is 60°)

图3 a和b与的关系Fig.3 Relationship between a and b with q/

2.2 光滑直线段

光滑直线段水面线常采用文献［10］的计算公式，即

式中:hp为势流水深;h为水深;δ为边界层厚度;Li为计算长度;ks为溢洪道的绝对粗糙度，在原型中一般取为0.427 ～0.610 mm.

2.3 台阶段

台阶式溢洪道上的水面线仍可用棱柱体明渠水面曲线的一般公式计算，即

式中:K0为流量模数;α为动能修正系数;ζ为局部阻力系数;Ed为流段下游的比能;Eu为流段上游的比能;J为流段的平均水力坡降;v，C，R分别为计算流段上下游断面的平均流速、平均谢才系数和平均水力半径;n为糙率;i=sinθ，θ为溢洪道坡度.

目前对台阶式溢洪道糙率还没有研究成果，本文采用曼宁－斯处克勒公式计算糙率，计算公式为

式中:对于台阶式溢洪道绝对粗糙高度ks=a0cosθ;a0为台阶高度(m).

动能修正系数α一般取为1.05～1.10，这里取为1.10.局部阻力系数ζ目前尚无研究成果，这里分别取为1.0，0.5和0进行计算，并根据计算和试验结果加以调整.

2.4 反弧曲线段

对于反弧段水深的计算，文献［11］曾做过研究，但其公式不完善，本文根据动量方程重新推导反弧段水深的计算公式.反弧曲线段如图4所示，断面1－1和2－2的动量方程为

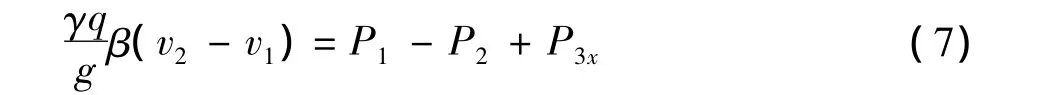
式中:v1和v2分别为断面1－1和2－2的平均流速;P1和P2分别为断面1－1和2－2的压力;P3x为反弧面上动水反力的水平分力.反弧面上的动水压力分弧面的离心力和反弧段水流的静水压力，两者方向均为向心方向.

图4 反弧段水力计算示意图Fig.4 Schematic diagram of hydraulic computation along flip bucket

式中:β0为反弧内离心力压强的校正系数.

式中:β 一般为1.02 ～1.05.为方便计算，β和β0均取为1.0，式(9)可进一步简化为

式(10)即为反弧段末端水深的迭代公式.

对于反弧末端接小挑坎的情况，P3x取负值，亦可根据动量方程求出挑坎末端水深的计算公式为

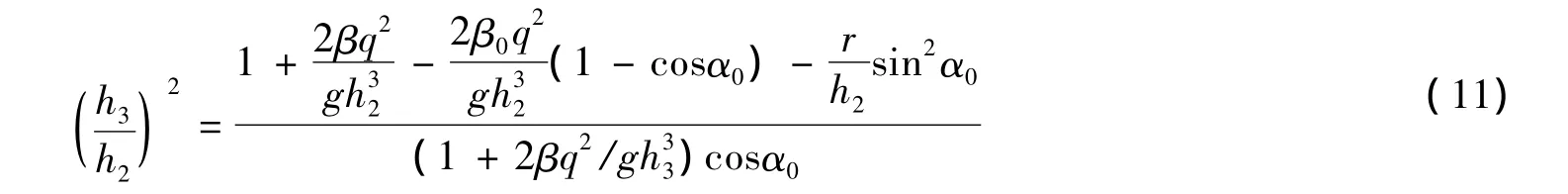
如果仍取β和β0为1.0，上式可进一步简化为

式中:h3为挑坎末端的水深;h2为反弧底部的水深;α0为反弧底部到反弧末端的夹角.

在以上推导反弧段水深时，离心力压强项中的水深应该取弧面平均水深，考虑到反弧段水深变化较小，为了推导方便，取水深为断面1－1的水深.计算和实测结果表明，误差不大(见算例4).

3 验证

算例1:某台阶式溢洪道采用WES曲线堰，堰上设计定型水头Hd=20 cm，台阶高度a0=5 cm，溢洪道坡度为51.3°，模型高度为203 cm，台阶数为33级.当堰上水头为30 cm，单宽流量为0.350 2 m2/s时，实测台阶起始断面水深为11.9 cm，试计算台阶段的水面曲线.

水面曲线用式(5)计算，糙率用式(6)计算，计算时取ζ分别为1.0，0和0.5，计算结果如图5所示.由图可见，与实测值相比，当ζ=1.0时，计算值偏大;当ζ=0时，计算值明显偏小;当ζ=0.5时，计算值与实测值吻合较好，所以可取ζ=0.5.

图5 堰上水头30 cm时不同ζ值计算水面线结果比较Fig.5 Comparison of flow profiles calculated by different ζ when weir head is 30 cm

为便于比较，图中还列出了用文献［9］和用边界层理论的计算结果.可见，文献［9］的计算结果与实测值相差较大;边界层理论计算的结果与实测值相差更大.说明在大坡度的台阶式溢洪道情况下，必须考虑坡度和局部阻力对水深的影响;而用边界层理论计算台阶式溢洪道上的水深显然不合适.

图中实测值从某一点开始水面线升高，即为掺气发生点，掺气发生点以后为掺气水流的水深.掺气发生点位置的确定见文献［12］，掺气水流水深的计算将另文撰写，本文仅讨论不掺气水流水面线的计算方法.

算例2:同算例1，台阶式溢洪道堰上水头为25 cm，单宽流量为0.260 2 m2/s，实测台阶起始断面水深为9.3 cm，取 α=1.1，ζ=0.5，水面曲线仍用式(5)计算.计算与实测结果见图6，图中L'为从起始台阶向下游的距离.可以看出计算所得的水面曲线与实测值吻合良好，而用文献［9］的公式和边界层理论计算结果仍与实测值相差较大.

图6 堰上水头25 cm时水面线计算结果比较(式(9)改为式(10))Fig.6 Comparison between the calculated results of flow profiles when weir head is 25 cm

算例3:高塘拱坝的台阶式溢洪道［13］.坝高110 m，台阶高度为0.9 m，溢洪道坡度为63.44°，溢洪道宽度为12.5 m，单宽流量为29.274 m2/s，实测第1级台阶起点水深为2.0 m，第30级台阶水深为1.5 m.用式(6)求得糙率n=0.035 83，由式(5)计算水深时，求得第30级台阶上的水深为1.41 m，比实测值小0.09 m，相差6%，而文献［13］的测量结果表明，台阶式溢洪道的掺气起始台阶在第27～30级台阶，所以水面略高于计算水深是正常的.

对于反弧段，由于实测台阶式溢洪道的水深在反弧段已为掺气水流的水深，无法获得清水水深，现按照文献［11］的光滑溢洪道测量值进行验算.

算例4:某光滑溢洪道反弧半径为30 m，反弧转角为47.87°，反弧起始水深分别为1.39 m和3.05 m，单宽流量分别为62.2和146.4 m2/s.由式(10)求得反弧末端水深分别为1.34和2.95 m，实测水深为1.35和3.00 m.可见，用式(10)计算反弧段的水深是可行的.

4 台阶式溢洪道全程水面曲线计算

根据以上公式，可以计算台阶式溢洪道全程水面线.图7是坡度为30°，51.3°和60°时水面曲线实测值与计算值的比较，图中实测值为掺气发生点以前的数值，掺气发生点以后，由于水面已为水气两相流，水面抬高较大，所以在图中隐去了掺气发生点以后的实测水深.由图可见，未掺气水流的水深计算值和实测值是比较吻合的.

图7 台阶式溢洪道计算值与实测值比较Fig.7 Comparison between the calculated and measured results of the stepped spillway

5 结语

通过对台阶式溢洪道水面线的分析和试验，认为计算台阶式溢洪道上的水深时，必须考虑局部阻力的影响，计算中采用局部阻力系数ζ分别为0，1.0和0.5，与试验结果对比，当ζ=0.5时计算值与实测值吻合良好，所以在台阶式溢洪道上水面线的计算中，可以采用ζ=0.5.

通过试验给出了坡度为30°～60°WES曲线段水面线的计算公式.通过动量方程得出的反弧段水面线的计算方法，与实测结果相符.

本文给出的台阶式溢洪道全程水面线的计算方法，除曲线段为经验公式外，在光滑直线段和台阶段，水面曲线的计算为工程中常用的理论公式，而没用采用经验公式，使公式具有通用性而避免了经验公式的局限性.这些通用公式对于模型和原型都是一样的.当然，在实际工程设计中，还需加上安全超高.

［1］骈迎春.台阶式溢洪道强迫掺气水流水力特性的试验研究［D］.西安:西安理工大学，2007.(PIAN Ying-chun.Model study on hydraulics of air-entraimented flow on stepped spillways［D］.Xi'an:Xi'an University of Technology，2007.(in Chinese))

［2］曾东洋.台阶式溢洪道水力特性的试验研究［D］.西安:西安理工大学，2002.(ZENG Dong-yang.Experimental investigation on the hydraulics of stepped spillways［D］.Xi'an:Xi'an University of Technology，2002.(in Chinese))

［3］HUNT S L，KADAVY K C，ABT S R，et al.Impact of converging chute walls for roller compacted concrete stepped spillways［J］.Journal of Hydraulic Engineering，2008，134(7):1000-1003.

［4］A.M.什瓦英什高.台阶式溢流坝及其消能［J］.水利水电快报，2000，21(6):1-6.(ШВАЙНШТЕЙН A M.Energy dissipation on stepped spillway［J］.Express Water Resources and Hydropower Information，2000，21(6):1-6.(in Chinese))

［5］韩彩燕.阶梯形溢流面上水流的初步分析［J］.华北水利水电学院学报，1995，16(4):51-56.(HAN Cai-yan.Preliminary analysis of flow in stepped spillway［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，1995，16(4):51-56.(in Chinese))

［6］RAJARATNAM N.Skimming flow in stepped spillways［J］.Journal of Hydraulic Engineering，1990，116(4):587-591.

［7］STEPHENSON D.Energy dissipation down stepped spillway［J］.International Water Power＆ Dam Construction，1991，43(9):27－30.

［8］罗启北.台阶式溢洪道上的水流分析［J］.贵州工学院学报，1996，25(3):64-69.(LUO Qi-bei.Analysis of the water flow in the stepped spillway［J］.Journal of Guizhou Institute of Technology，1996，25(3):64-69.

［9］付奎，刘韩生，杨顺玉.台阶式溢洪道滑掠水流水面线计算公式初探［J］.人民黄河，2009，31(6):117-118.(FU Kui，LIU Han-sheng，YANG Shun-yu.Water surface profile calculation of skimming flow on stepped spillway［J］.Yellow River，2009，31(6):117-118.(in Chinese))

［10］华东水利学院.水工设计手册6:泄水与过坝建筑物［M］.北京:水利电力出版社，1987.(East China Technical University of Water Resources.Handbook of hydraulic structure design(6):Barrages，spillways and control works［M］.Beijing:Hydraulic and Electric Power Press，1987.(in Chinese))

［11］黄智敏.溢流坝水面线计算分析和观测［J］.水动力学研究与进展:A辑，1998，13(3):31-36.(HUANG Zhi-min.Calculation analysis and observation on spillway dam hydraulic grade line［J］.Journal of Hydrodynamics(SerA)，1998，13(3):31-36.(in Chinese))

［12］徐啸.分流齿墩掺气设施与台阶式溢洪道联合应用水力特性的研究［D］.西安:西安理工大学，2011.(XU Xiao.Research on hydraulic characteristics of stepped spillway combined with splitting dental-pier aerator［D］.Xi'an:Xi'an University of Technology，2011.(in Chinese))

［13］才君眉，薛慧涛，冯金鸣.碾压混凝土坝采用台阶式溢洪道消能初探［J］.水利水电技术，1994(4):19-21.(CAI Junmei，XUE Hui-tao，FENG Jin-ming.A preliminary study on stepped spillway on RCC dam for dissipation［J］.Water Resources and Hydropower Engineering，1994(4):19-21.(in Chinese))