大型压机液压同步平衡系统可靠性分析

2012-11-18王建国杨固川

中国重型装备 2012年4期

王建国刘军杨固川

(中国第二重型机械集团公司设计研究院，四川 618000)

大型压机是满足我国各类基础建设所需的重大装备。同步平衡控制系统是大型模锻压机的重要特征，其作用在于控制活动横梁在工作过程中产生的倾斜度。一旦倾斜度超过设备设定控制精度要求，平衡系统立即纠偏，使其水平度保持在较高的精度范围内，以保证模锻件所需要的尺寸精度，有利于改善液压机机械设备本体的受力状况，延长大型压机的维护周期及使用寿命。

1 大型压机平衡液压系统特点

大型压机液压系统庞大，压力高，流量大，液压控制系统的设计需要解决液压元件的选型及系统配置要求等难题。同步平衡控制系统是大型压机的核心所在，压机活动横梁的位置检测靠位移传感器实时检测。横梁在运行过程中一旦某个角位置精度超过设定目标值，将通过液压伺服控制进行纠偏。

2 液压可靠性设计

可靠性是产品研发的基础，贯穿于产品的设计、制造、使用和维护的全过程，液压系统的可靠性依赖于设计、制造、使用维护以及管理等多种因素，但归根到底要首先依赖于液压系统设计的可靠性。因系统的固有可靠性为设计所确定，制造与使用维护等只能达到或保持系统的固有可靠性，这就是液压系统的可靠性设计的重要意义所在。

为了保证液压系统的可靠性，针对压机的不同部位提出了具体要求，根据不同部位的重要性及工况，要求的可靠性程度不一样，对同步平衡控制系统的可靠性要求较高，在设计压机液压控制系统时作了充分的论证。

3 液压系统可靠度计算

3.1 元件可靠度的确定

可靠度是指产品在规定的条件下和规定的时间内，完成规定功能的概率，它是时间的函数，记作R(t)。失效率是指产品工作到t 时刻后的单位时间内发生失效的概率，记作λ(t)。液压系统在调试完毕后，在正常工作阶段，失效率为恒定值，可靠度R(t)=exp(-λt)，是指数分布。

计算系统的可靠度，必须确定每个组成元件的可靠度，一般根据表1 的数据选取。表中所给出的为元件基本失效率，该值在标准实验室测得，为基本故障率λ0;实际的失效概率应考虑环境系数K，实际的失效概率λ=Kλ0，K 为环境系数，这里取K=5。

3.2 建立系统的可靠性逻辑图

根据同步平衡控制系统的原理，系统中各个元件都发挥着重要的功能，每个元件出现故障时，都可能引起整个系统出现故障，严重时可能导致系统无法继续工作。以同步平衡系统工作时的相互逻辑关系为依据，根据大型压机液压系统各元件的功能及相互关系，建立系统的可靠性逻辑模型。可靠性逻辑框图见图1。

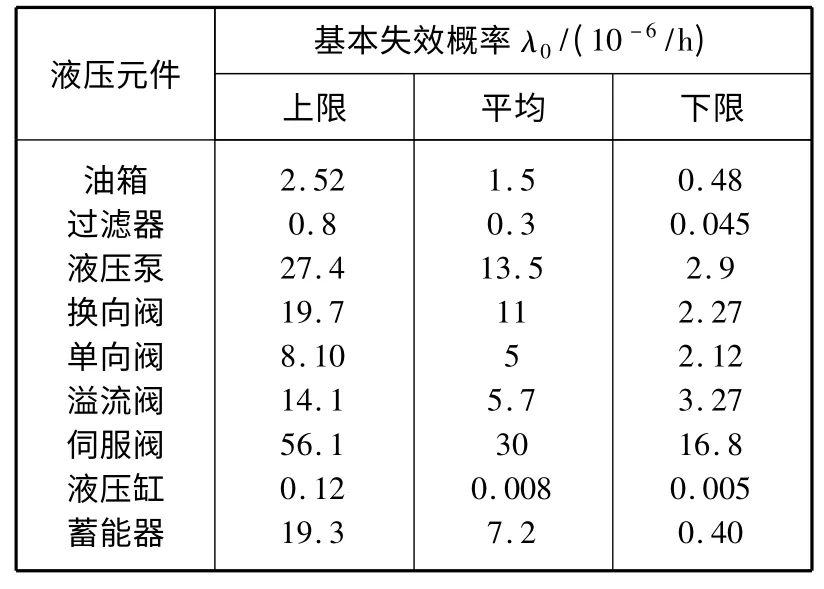
表1 液压元件的基本失效率λ0Table 1 Level failure rates λ0of hydraulic components

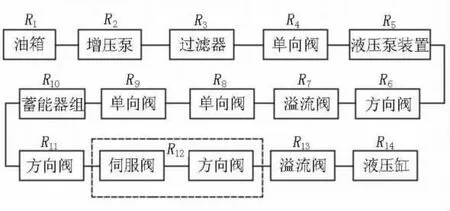
图1 液压系统可靠性逻辑框图Figure 1 Logical block diagram of hydraulic system reliability

3.3 液压系统可靠性的计算方法

为了使可靠度的计算过程简便，特提出如下假设:系统管路的失效率为0;电气控制部分的可靠度为1;液压元件和系统只有两种状态，正常和故障状态，没有中间状态;系统中各元件的故障相互独立;不考虑人为故障及外界干扰。

(1)串联系统的可靠度计算

由n 个元件组成的串联系统的可靠度:

R(t)=R1(t)R2(t)……Rn(t)

(2)并联系统的可靠度计算

由n 个元件组成的并联系统的可靠度:

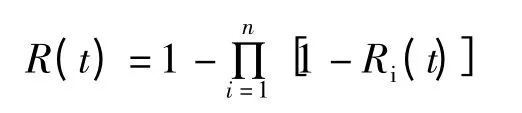
3.4 同步平衡系统可靠度的计算

根据系统的可靠性逻辑图，基本失效率λ0按表1 中给出的平均数值选取，建立各部分的数学模型。

其中，蓄能器组的可靠度为:

R10=［exp(-2.47×10-6×k×t)］{1-［1-exp(-7.2×10-6×k×t)］10}

伺服阀与单向阀串联的可靠度为:

R12=1-［1-exp(-1.6×10-6×k×t)］3

系统总的可靠度为:

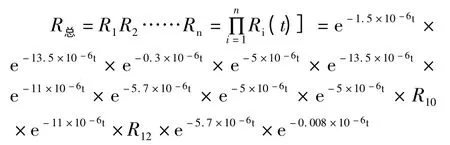
系统工作时间与可靠度的对应关系见表2。根据以上计算结果，一般液压系统连续工作约600 h 左右就要进行技术保养，此时的可靠度为0.735 9，工程机械液压系统的可靠度一般为0.6～1，因此，该液压系统的工作可靠性是满足要求的。若考虑到此系统选用的进口元件，制造质量好，油液清洁度高，将元件的失效率λ0取下限值来计算，可靠度将提高到0.909 4。

表2 系统工作时间与可靠度的对应关系Table 2 The corresponding relation of working time and reliability of system

3.5 液压系统平均无故障工作时间的计算

根据以上系统可靠度的计算，可以计算出系统的平均无故障工作时间:

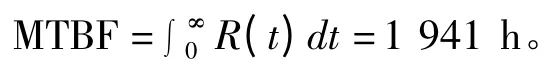
当环境系数为5 时，λ0取平均值时，液压系统的平均无故障时间为1 941 h，从理论上来看，系统工作1 941 h 后应进行检查、维修;当λ0取下限值时，MTBF=5 492 h;当环境系数为10 时，λ0取下限，MTBF=2 746 h。从以上分析可知，环境条件越好，系统可靠性越高，液压元件质量越高，元件的失效率越低，系统的可靠性就越高。

3.6 液压系统的可靠性仿真

根据液压系统的可靠性模型，用Matlab 仿真软件进行分析，绘制出可靠度曲线图，环境因子和元件失效率取几种不同的数值对比，绘制出可靠度曲线图，见图2 和图3。

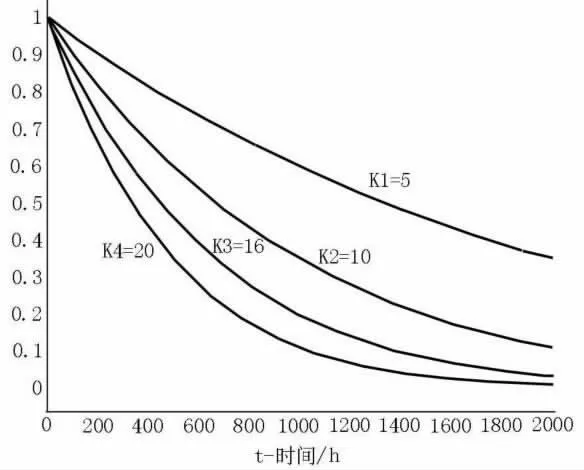
图2 λ0取平均值的可靠度曲线Figure 2 Reliability curve when λ0is the mean value

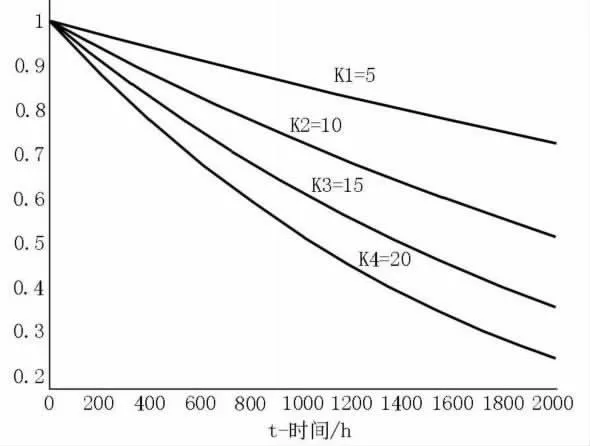
图3 λ0取下限值的可靠度曲线Figure 3 Reliability curve when λ0is the lower value

通过可靠度曲线图，可以看出工作环境越差，系统中各元件的故障率增加，整个系统的可靠度下降;采用质量较好的液压元器件，系统组成元件的失效率降低，也是提高系统可靠性的有效途径之一，但第一次投资费用较大。液压系统在工作中70%左右的故障率是由系统油液污染引起的，因此，在工作中应及时跟踪油液清洁度，保证系统油液的清洁度，也是提高系统可靠度的有效措施。