三相电压型逆变器模型预测电流控制

高 林，张 凯，张 磊，方之轩，庙延民，吴治立

（1.酒钢集团宏兴钢铁股份公司西沟矿， 甘肃嘉峪关市 735100；2.云南磷化集团有限公司昆阳磷矿，云南昆明 650600；3.栾川钼业集团股份有限公司矿山公司， 河南洛阳市 471500）

三相电压型逆变器模型预测电流控制

高 林1，张 凯1，张 磊1，方之轩2，庙延民2，吴治立3

（1.酒钢集团宏兴钢铁股份公司西沟矿， 甘肃嘉峪关市 735100；2.云南磷化集团有限公司昆阳磷矿，云南昆明 650600；3.栾川钼业集团股份有限公司矿山公司， 河南洛阳市 471500）

针对目前电力电子系统中常用的滞环控制方法开关频率不固定的现象，提出了一种新的模型预测控制算法（S－MPC）。该算法采用离散时间模型，预测电力电子变换器中控制对象未来的数值，根据不同的控制对象特性以及约束条件，选择不同的优化函数来决定变换器的开关状态。以三相电压型逆变器输出电流为控制对象，建立预测控制模型、控制性能优化函数，并在MATLAB／SIMULINK上分别对S－MPC和滞环控制进行对比仿真研究。仿真结果表明，新型S－MPC算法能够准确地跟踪参考电流，解决了常用方法中存在的电流耦合情况，实现了电流解耦控制，达到了较好的控制效果，具有一定的应用价值。

模型预测控制；电力电子变换器；脉宽调制；电流控制

0 引 言

电力电子与电力传动控制技术在新能源与分布式发电、变频驱动、智能电网等方面得到广泛应用［1－3］。但是由于受数字信号处理器运算能力的限制，传统的控制方式主要有滞环控制、线性PWM控制等方法［4］。近年来，随着数字信号处理器运算速度的提高，出现了新型的控制方法，如模糊控制、自适应控制，滑模变结构控制、预测控制等方法［5－7］。

预测控制是一种基于模型的优化闭环控制方法，它利用系统模型预测控制变量未来的数值，根据优化控制策略，选择合适的控制动作。由于采用了滚动的有限时段优化取代一成不变的全局优化，其更能适应实际过程，具有更强的抗负载扰动能力。早期的电力电子预测控制器是选用模型预测取代线性控制的无差拍控制［8－10］。

模型预测控制（MPC）对非线性系统以及系统约束条件的适应性强，系统响应速度快，抗干扰能力强。文献［11］提出一种广义预测控制（GPC）方案，简化系统模型，降低计算量，得到较好的效果，但是GPC对处理控制约束条件以及系统非线性的能力较差。

本文提出一种简易的电力电子模型预测控制算法（S－MPC）。该算法采用离散时间模型来预测控制变量在变换器各个状态下的未来数值，同时考虑控制性能指标函数的约束条件，选择使性能指标最优的开关组合为下一时刻的开关状态，消除数字控制中的采样延时。

1 S－MPC工作原理

在电力电子系统中，假定变换器的控制信号为s（t），系统输出量为x（t），输出量的参考值为x＊（t）。控制目的是变换器在s（t）的作用下，系统的输出量x（t）无限接近参考值x＊（t）或者是在x＊（t）处镇定。考虑到数字化控制离散采样的特点，假定在第k个采样周期，x（t）的采样值为x（tk）；变换器共有n种控制信号si，i＝1…n；系统的预测模型为xpi（tk＋1）＝fp｛x（tk），si｝，i＝1…n，xpi（tk＋1）为系统在控制信号si的作用下，在第k＋1采样时刻的模型预测输出；预测系统性能指标优化函数为g＝fg｛x＊（tk＋1），xpi（tk＋1）｝，i＝1…n。

S－MPC工作原理是在第k个采样时刻tk，测量输出x（tk），参考输出x＊（tk），通过模型预测控制算法，结合变换器的n种控制信号，预测在每一种控制信号si作用下，系统在下一采样时刻tk＋1的输出xpi（tk＋1），然后根据性能指标约束函数g，选择使性能指标最优的si作为本采样时刻的控制信号，使系统的输出最优跟踪参考输出x＊（t）。图1为SMPC示意图。在第k个采样周期，xp3（tk＋1）最接近参考值x＊（tk＋1），所以在tk时刻，控制信号s3作用于变换器；在第k＋1个采样周期，xp2（tk＋2）最接近参考值x＊（tk＋2），所以在tk＋1时刻，控制信号s2作用于变换器。

图1 理想的S－MPC工作原理

2 三相逆变器模型预测电流控制

2.1 逆变器数学模型

三相电压型逆变器电路如图2所示，其中负载为三相对称非线性带反电动势负载，三相输出电流分别为iLa、iLb和iLc，L和R分别为三相对称负载的电感与电阻，三相对称反电动势分别为ea、eb与ec。

图2 三相电压型逆变器

假定控制信号si为逆变器的开关驱动信号，设si的二值逻辑关系为：

将开关驱动信号用空间矢量形式表示，由等量变换可得：

其中：α＝ej2π／3。

逆变器输出三相电压分别为：

将三相输出电压写成空间矢量的形式，得：

考虑到逆变器的控制信号sa、sb、sc共有8种组合，产生8个电压空间矢量，其中sasbsc＝000与sasbsc＝111产生了零矢量，即v0＝v7。图3为逆变器输出电压空间矢量图。

图3 逆变器输出电压空间矢量

预测控制器将逆变器的非线性特点考虑在预测模型中，逆变器为离散系统，并且只有7种开关矢量。为建立简易模型，便于理论推导，本文在推理过程中忽略实际应用中的同一桥臂存在死区的现象。

2.2 负载模型

如图2所示，由KVL定理可知

由式（8）可得到输出电压空间矢量v。

逆变器输出电流空间矢量为：

负载反电动势的空间矢量为：

由式（8）、（9）、（10）、（11）可以得到输出电流的空间矢量方程为：

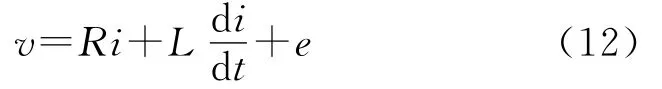
2.3 电流预测模型

假定采样周期Ts远远小于电网电压周期，微分di／dt可以近似写成：

在S－MPC的预测中，将方程式（13）离散化，第k个采样周期的方程为：

将式（14）前移一个采样周期，则变成：

方程式（15）构成了逆变器的电流预测模型。但在式（15）中，反电动势e（k＋1）为未知，并且反电动势e不可测量，所以必须对反电动势e进行在线估算。由式（14）可知，在第k个采样周期，v（k）、i（k）由测量可以得到，i（k－1）为前一采样时刻的历史数据，所以，第k个采样时刻的反电动势可以在线估算得到，为：

考虑到采样周期Ts远远小于电网电压周期，可以近似地认为。

2.4 电流参考轨迹

电流平均值控制法容易导致较大的输出纹波，输出纹波的大小取决于采样周期测量的初始值与控制周期的平均参考值的差值；末端输出控制法虽能产生较小的输出纹波，但带来输出平均值的延时。本文采用末端输出控制方法，下一采样时刻参考电流值可以由二阶线性插值预测得到：

2.5 性能指标优化

在模型预测控制算法式（15）中，v（k＋1）未知，根据变换器的状态，v（k＋1）共有7种电压矢量，为达到控制目的，使得控制性能最优，必须从7种电压中选择1个电压矢量作为在（k＋1）时刻的控制信号。

在本文中，为使输出误差最小，选择性能指标优化函数为：

3 仿真结果

为验证上述控制算法的正确性，采用Matlab／Simulink构建系统模型进行仿真研究。

仿真主要参数为：直流电压Vdc＝150V，负载电阻R＝1Ω，负载电感为L＝10mH，反电动势幅值为Em＝15V，频率为f＝50Hz。输出参考电流的幅值为Im＝20A，频率为f＝50Hz。

为说明该算法的有效性，本文将模型预测电流控制与传统的滞环控制法进行对比分析，当仿真时间t＝0.015s时，系统输出参考电流的分量由幅值Im＝20A变为Im＝10A，分量保持不变。图4为S－MPC的动态波形，图5为滞环控制动态波形，电流滞环容差宽度为δ＝±0.3A。可以看出，滞环控制与S－MPC控制的动态响应速度较快。当发生变化时，从iβ的波形可以发现，滞环控制的iβ受到变换的影响，说明滞环控制方式iα，iβ分量存在耦合情况，而由S－MPC的iβ波形发现，它并没有受到变化的影响，说明这两个分量之间是独立的，实现了解耦控制。同时从图4（b）可以发现，iβ几乎无误差的跟踪指令电流。

图4 S－MPC负载电流动态波形

图5 滞环控制负载电流动态波形

4 结 论

提出了适用于电力电子系统的简易模型预测控制方法，并对该控制算法的工作原理进行了详细分析。以三相电压型逆变器电流控制为例，构建仿真模型对该控制算法进行了仿真验证，结果表明：该控制算法相对于常用的滞环控制具有更好的静、动态性能，能实现控制分量的解耦，且因其采用了离散预测模型，因而使其更加贴近实际的数字控制系统，解决了数字控制系统中的采样延时等问题，具有较好的实际应用价值。

［1］Wu B，Pontt J，Rodriguez J，et al.Current Source converter and cycloconverter topologies for industrial medium－voltage drives［J］.IEEE Trans.Ind Electron，2008，55（7）：2786－2797.

［2］戴训江，晁 勤，樊艳芳.基于阻尼谐振的光伏并网逆变器谐波补偿控制［J］.电力自动化设备，2011，31（1）：79－83，94.

［3］夏向阳，罗 安.单注入式APF直流侧电压的稳定控制［J］.电力自动化设备，2009，29（1）：33－36.

［4］Holtz J.Pulse width modulation for power converter［J］.Proc.IEEE，1994.82（8）：1194－1214.

［5］李光叶，万健如，刘英培，等.基于模糊零矢量永磁同步电机直接转矩控制［J］.电力自动化设备，2009，29（9）：31－35.

［6］周 鑫，郭源博，张晓华，等.基于自适应跟踪控制的三相电压型PWM整流器［J］.中国电机工程学报，2010，30（27）：76－82.

［7］王晓刚，谢运祥，帅定新，等.基于模型预测控制的三相四桥臂有源电力滤波器［J］.华南理工大学学报（自然科学版），2009，37（11）：56－63.

［8］Yang S M，Lee C H.A deadbeat current controller for field oriented induction motor drives［J］.IEEE Trans Power Elextron，2002，17（5）：772－778.

［9］Malesani L，Mattavelli P，Buso S.Robust dead－beat current control for PWM rectiffier and active filters［J］.IEEE Trans.Ind Appl，1999，35（3）：613－620.

［10］Mattavelli P.A inproved deadbeat control for UPS using disturbance observers［J］.IEEE TransInd Electron，2005，52（1）：206－212.

［11］杨俊华，冯小峰，吴 捷，等.基于广义预测的矩阵变换器电流闭环控制［J］.电力自动化设备，2010，30（9）：28－32.

［12］Jose Rodriguez，Jorge Pontt，Cesar A，et al.Predictive Current Control of a Voltage Source Inverter［J］.IEEE Trans Ind E－lectron，2007，54（1）：495－503.

2012－08－09）

高 林（1972－），男，甘肃嘉峪关人，工程师，从事电气工程方面的研究工作，Email：zxp836＠163.com。