多面体模型的Eros433 引力场计算与分析
2012-11-16崔祜涛张振江
崔祜涛,张振江,余 萌
(哈尔滨工业大学 深空探测基础研究中心,150080 哈尔滨,river18202@gmail.com)
形状不规则是小行星与类球形大行星的主要区别之一,不规则形状使得小行星的引力场非常复杂.这不但给研究卫星在小行星引力场中的运动规律带来了非常大的困难,也使得绕小行星卫星轨道的设计问题变得异常复杂.因此,建立小行星引力场模型不但是小行星探测中所要解决的关键问题,更是研究小行星卫星轨道动力学和设计小行星卫星轨道的基础.传统方法很难对形状如此复杂的小行星引力场建模,随着计算机科学的发展,特别是近20 年来计算机3D 建模与仿真技术的提高,使得精确地建立小行星引力场成为可能[1].到目前为止,常用的小行星引力场建模方法按其本质可分为两大类:第一类是采用无穷级数逼近小行星的引力势函数,常用的有球谐函数法[2]和椭球谐函数法[3];第二类方法是用可计算引力势能的模型来逼近小行星的形状,然后求得近似模型的引力势函数.这类方法主要有三轴椭球体法[4]和多面体模型法.地球引力场建模常用第一类方法,但对于小行星而言,应用第一类方法存在两个问题,一是缺乏环绕轨道数据来确定(椭)球谐系数,二是在接近小行星表面(布里渊(椭)球[3]以内)时,谐函数方法的计算结果会存在较大误差甚至发散.三轴椭球体方法的缺点是椭球体与小行星形状相似度差,精度不高.
为解决上述方法存在的问题,R.A.Werner[5]和P.S.RYAN[6]提出用多面体来逼近小行星的形状进而求其引力势能的方法,2002 年Miller 等[7]研究了应用地面天文观测确定小行星的形状、自旋情况、类别和密度等参数的方法.2006 年E.G.Fahnestock 等[8]应用多面体模型方法对不规则形状双星系统的绕飞轨道进行仿真计算.2009 年胡维多[9]系统地分析了近小行星区域的动力学环境及其对环绕小行星飞行器轨道的影响情况.为解决小行星探测任务前无法获得高精度引力场球谐系数的问题,笔者在2010 年提出一种基于多面体模型的不规则形状小行星引力场球谐系数的求取方法[10].Shao Wei[11]提出一种利用三维散乱点对小天体表面进行三角剖分,并建立小行星多面体模型的方法.
1 小行星形状与多面体模型
图1 为美国近地小行星交会任务(Near Earth Asteroid Rendezvous Mission,NEAR)的苏梅克探测器(Shoemaker spacecraft)在2000 年2 月12 日从距离Eros433 小行星1 800 km 之外所拍摄的一系列照片中的6 幅.由图1 可知,Eros433 小行星的形状极不规则,事实上,太阳系中绝大多数小行星的形状都不规则.为了尽可能精确地描述小行星的形状,可以使用1 个表面由一系列三角形构成的多面体来逼近小行星,这个多面体即为小行星的多面体模型.仿真证明,当多面体由5 184 个面构成时,已经可以较好地逼近Eros433 小行星的形状.在本文的分析计算中,应用的多面体模型包含49 152 个面.读者可以在NASA 的Planetary Data System 中获得更多的小行星多面体模型.
多面体模型可以通过分析小行星照片获得[12],这些照片可以是地面天文台拍摄的[13],也可以是掠飞过程中卫星拍摄的.对于已经探测的小行星,探测器的激光雷达可以提供更为精确的多面体模型[14].多面体模型可以充分利用地面天文观测或掠飞任务所拍摄的小行星图像信息,因而在任务设计阶段就可以取得较高的精度.

图1 Eros433 全貌照片
2 多面体模型引力势能的计算
小行星引力场建模实质为求取引力场中任意检验点P(x,y,z)处的引力加速度函数F(x,y,z)的过程.而引力加速度可由引力势能V(x,y,z)得到,二者的关系为

式(1)表明小行星引力场中某一点的引力加速度F(x,y,z)等于该点引力势函数对位置的偏导数,即引力势函数的梯度.这样,引力场建模问题就转化为求小行星引力场中任意检验点引力势函数的问题.
图2 为引力势能函数计算的矢量图.
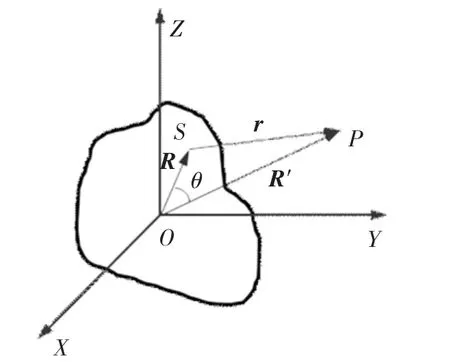
图2 引力势能函数的计算
如图2 所示,检验点P 在小行星固连坐标系下的位置矢量为R' =[x y z]T,大小用R'表示.欲求此点的引力势能,可以将中心天体分解成若干小体积微元,则每个体积微元可以看成1 个质点,设1 个质量记为dm 的体积微元S 在小行星固连坐标系内的位置矢量为R=[ξ η ζ]T,大小用R 表示.则由检验点到该体积微元的矢量为r=[x-ξ y-η z-ζ]T,大小用r 表示,检验点处的引力势能可由下面三重积分定义[15]:
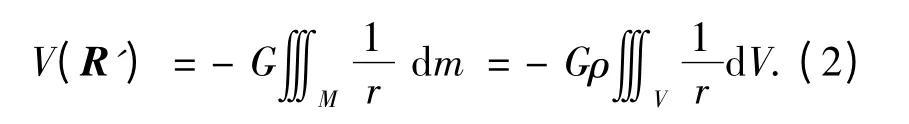

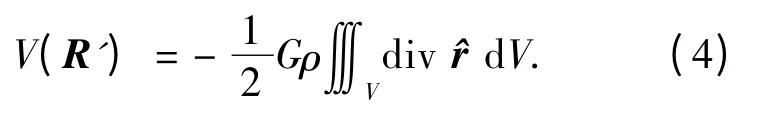
应用高斯公式,式(4)中的三重积分可以转化为曲面积分,即

对于多面体模型而言,式(5)中的曲面积分可以写成如下形式:

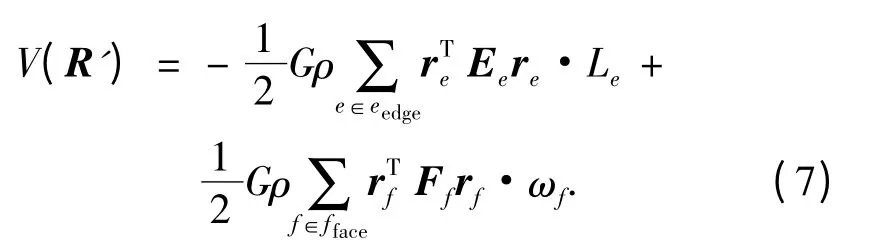
式中eedge表示边,re为多面体边e 上任意一点到检验点的矢量,且

其中Ee为3×3 矩阵;^nA为面A 的外法线方向矢量为在面A 内的边e 的外法线方向矢量;re1、re2为检验点到边的两个端点的距离;e12为边e 的长度;^nf为面f 的外法线方向矢量;Ff为3×3矩阵.
图5(a)~图5(c)分别是轴承3种运行状态下某一采样样本的双谱时频图.图5中可以看出,虽然轴承在不同故障运行状态下双谱图存在很大差异,可以为后续SVDD诊断所需的特征提取提供很好的素材.但由于滚动轴承复合故障运行状态下,各个单个故障信号之间的相互干扰极有可能出现耦合现象,很难直接在其双谱时频图上提取有效的故障特征信息.
上面就是多面体模型计算引力势能的全部公式,下面介绍一下引力加速度和其梯度的计算公式.

式(9)是用来计算引力加速度的,式(10)为引力加速度的梯度矩阵.式(10)中的▽2V(R')称为引力场拉普拉斯算子,它等于引力梯度矩阵的迹.根据拉普拉斯算子的值可以方便的判断检验点是否位于多面体模型的外侧.判断准则如下式所示.

3 Eros433 引力场计算与分析
`本文计算中使用的Eros433 小行星多面体模型来源于NASA 的Planetary Data System.数据共包含4 个不同精度的多面体模型,面的个数分别为49 152,196 608,786 432,3 145 728.为减小计算量,节约时间,本文应用49 152 个面的多面体模型进行计算.
3.1 引力场计算
NASA 提供的数据包中的内容共分两部分,第一部分为多面体表面上点的位置列表,如数据包中第1 个点为“1 8.332 72E+00-4.809 02E+00-4.784 54E+00”,其中1 表示该点的编号,后面3 个数为该点在小行星固连坐标系中的位置分量,单位为km;第二部分为组成多面体的三角形索引,如其中1 个三角形表示为“1 1 105 101”其中第1 个1 表示该三角形编号,后面3 个数表示三角形的3 个顶点的编号,查询第一部分即可确定该三角形在小行星固连坐标系中的位置.
根据此数据包提供的数据,结合上文给出的公式,即可计算多面体模型外任意一点的引力势能和引力加速度.计算中首先应用式(11)测试检验点是否位于多面体外侧,对于位于外侧的检验点,应用式(7)和式(8)求其引力势能和引力加速度.小行星的密度取为2 670 kg/m3,计算结果如图3 ~图10 所示.在引力加速度的等高线图中,颜色用来表示引力加速度的大小,箭头表示引力加速度的方向.
图3 ~4 分别为小行星固连坐标系的XOY,YOZ,ZOX 三个坐标平面内的引力势能与引力加速度的分布情况,由这6 幅图像可知,Eros433 小行星引力场中引力势能和引力加速度的分布都不规则.小行星表面的引力加速度分布也极不均衡,最大加速度与最小加速度相差近三倍,而且引力加速度的方向也较复杂,南半球的表面平坦区域,引力大体上与小行星表面垂直,而在北半球的巨大凹槽处,引力的方向与小行星表面的夹角最大.

图3 Eros433 小行星在坐标平面内引力势能分布
图5 ~6 为距离质心18 km 的球面上Eros433小行星引力势能和引力加速度的分布情况.由这两幅图像可知,在半径为18 km 处,引力加速度存在3 个极大值(图6 中点A,B,C 周围)区域和两个极小值(图6 中点D,E 周围)区域.引力加速度最大的区域大约位于西经165°的赤道(点A)附近.两个极小值区域位于西经75°的南半球和东经100°的北半球附近.在这些重力异常区,卫星的轨道会受到很大的影响,轨道根数可能在短时间内发生较大的变化,这与绕大行星的卫星轨道有很大区别[16].

图4 Eros433 小行星在坐标平面内引力加速度分布
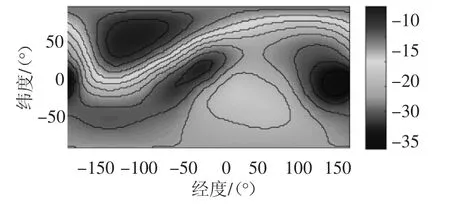
图5 R=18 km 的引力势能分布
3.2 对比分析
上文给出了应用多面体模型方法计算得到的Eros433 小行星引力场的分布情况,为检验算法的准确性,将上述计算结果与JPL 实验室公布的Eros433小行星16 阶引力场模型进行对比.该引力场模型根据苏梅克探测器对小行星近一年的环绕飞行的轨道数据和探测器上携带的激光高度计的观测值综合计算得到.由于在小行星表面附近(布里渊球内)球谐函数发散,因此无法计算贴近小行星表面区域的引力势能,所以这里只比较两种方法计算的距小行星质心18 km 处的引力势能值之间的差.其结果如图7 所示.
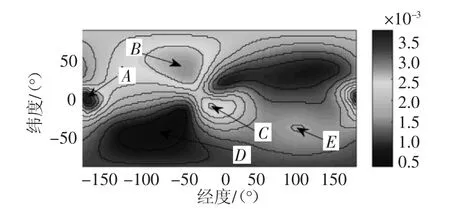
图6 R=18 km 的引力加速度分布

图7 R=18 km 时两种方法计算结果的偏差
由图7 可知两种方法计算得到的引力势能误差非常小,经计算表明,最大相对误差出现在小行星的长轴一端附近,对应于图6 的A 点附近区域,其最大误差为1.52%,其余区域的最大误差均不超过0.5%.这充分说明本文方法具有较高的计算精度.为清楚的描述计算误差与小行星形状间的关系,将误差曲面投影到Eros433 表面,可以得到小行星表面的误差分布图,如图8 所示.
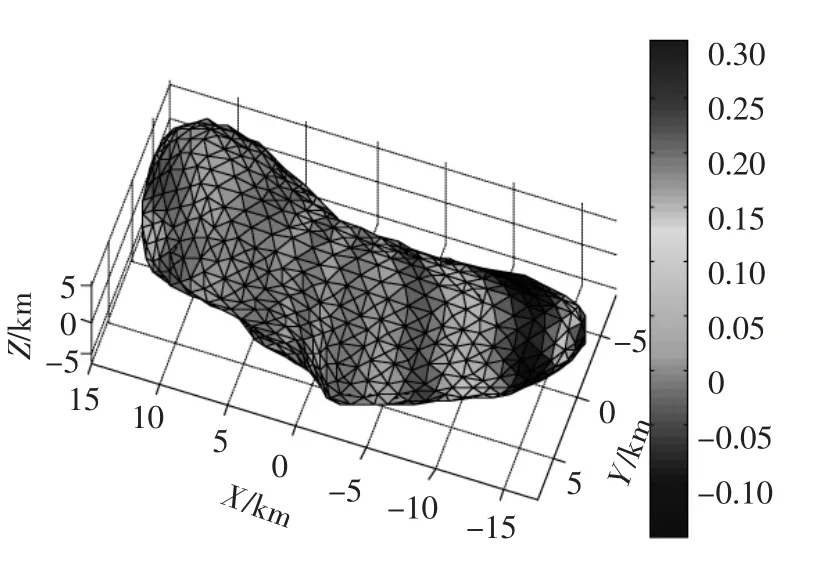
图8 计算误差在小行星表面的分布
3.3 伪势能与平衡点
除了不规则的形状外,小行星的自旋对绕其运动的卫星轨道亦有很大的影响,这两个因素相互叠加,使得小行星卫星的轨道动力学变得异常复杂.在小行星固连坐标系中,卫星的运动方程为[21]
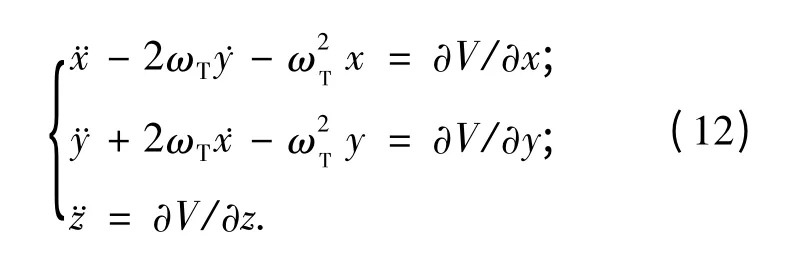
其中[x y z]T为卫星在小行星固连坐标系中的位置矢量;ωT为小行星的自旋角速度,Eros433的自旋角速度为ωT=3.311 7×10-4rad/s;V 为前文建模的引力势函数.运动方程(12)存在如下形式积分[17]:

其中J 称为Jacobi 积分常数;0.5(˙x2+˙y2+˙z2)为飞行器的动能,由式(13)右端的前两项的和可以定义飞行器的伪势能,其形式为

伪势能描述了旋转坐标系中的引力场分布情况,因为考虑了小行星自身旋转对引力场的影响,伪势能可以比引力势能更好的描述小行星的引力场状况.图9 为Eros433 小行星赤道平面内的伪势能曲面,图10 为伪势能的等高线图.由式(13)可知伪势能U 相当于动能为零时的jacobi 积分常数J,因此,图10 又称为零速度曲线图.

图9 Eros433 小行星伪势能曲面
图9 ~11 反映了赤道平面内的伪势能分布情况,由图9 可知,在小行星外侧,随着与小行星距离的增大,伪势能先减小后增大,在Y 轴附近,存在两个伪势能的极小值点(对应于图10 中的E3,E4).而在X 轴附近,伪势能曲面存在两个鞍状平衡点(对应于图10 中的E1,E2).这4 个点称为平衡点,由图11 可知,在平衡点附近,伪势能分布情况复杂,因此在此区域内运动的卫星轨道受其影响表现出强烈的非线性,这些轨道往往是不稳定的[18].E1~E4四个平衡点的性质与圆型限制性三体问题中的动平衡点性质相似.故在其周围也存在周期轨道和拟周期轨道,笔者在文献[19]中研究了E1、E2两个平衡点附近的轨道特性和轨道控制问题.Scheeres 在文献[20]研究了平衡点附近周期轨道的确定与计算问题.

图10 Eros443 零速度曲线和平衡点

图11 平衡点E2 点附近伪势能的分布
4 结 论
本文介绍了基于形状逼近的小行星引力场建模方法——多面体模型法.给出了Eros433 小行星的多面体模型,并推导了多面体模型方法中引力势能、引力加速度和拉普拉斯算子的计算公式.应用 NASA 的 Planetary Data System 提供的Eros433小行星多面体模型分析了其引力场分布情况,绘制了引力势能和引力加速度的分布图.考虑到小行星旋转对引力场的影响,本文还分析了小行星赤道平面内伪势能曲面与零速度曲线分布情况.由以上分析可知:
1)Eros433 小行星表面的引力加速度分布极不均衡,最大加速度与最小加速度相差近三倍,而且引力加速度的方向也较复杂,南半球的表面平坦区域,引力大体上与小行星表面垂直,北半球的巨大凹槽处,引力的方向与小行星表面存在很大的夹角.
2)在距离小行星中心18 km 处,引力加速度存在3 个极大值和2 个极小值.其中引力加速度最大的区约位于西经165°的赤道附近,2 个极小值分别位于南半球的西经75°和北半球的东经100°区域.
3)在自旋和不规则形状的共同影响下,Eros433小行星引力场中存在4 个平衡点,其中2 个平衡点位于Y 轴附近,对应于伪势能的极小值;另外2 个位于X 轴附近,与之对应的伪势能曲
面呈马鞍面状分布.
[1]ZUBER M T,SMITH D E,CHENG A F.The shape of 433 Eros from the NEAR-shoemaker laser rangefinder[J].Science,2000,289(5487):2097-2100.
[2]STEFANO C,SUSANNA M.Methods for computing the potential of an irregular,homogeneous,solid body and its gradient[C]//AIAA/AAS Astrodynamics Specialist Conference.Denver,CO:AIAA,2000:4-17.
[3]GARMIER R,BARRIOT J P.Ellipsoidal harmonic expressions of the gravitational potential:theory and applications[J].Celestial Mechanics and Dynamical Astronomy,2001,79(4):235-275.
[4]SCHEERES D J.Dynamics about uniformly rotating triaxial ellipsoids.Applications to Asteroids[J].Icarus,1994,110(2):225-238.
[5]WERNER R A,SCHEERES D J.Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 castalia[J].Celestial Mechanics and Dynamical Astronomy,1997,65(3):313-44.
[6]RYAN S P,ROBERT A W,BHASKARANZ S.Estimating small-body gravity field from shape model and navigation data[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Honolulu,Hawaii:AIAA,2008,AIAA-2008-6603.
[7]MILLER J K,KONOPLIV A S,ANTREASIAN P G.Determination of shape,gravity,and rotational state of asteroid 433 Eros[J].Icarus,2002,155(1):3-17.
[8]FAHNESTOCK E G,TAEYOUNG L,MELVIN L.Polyhedral potential and variational integrator computation of the full two body problem[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Keystone,Colorado:AIAA,2006,AIAA 2006-6289.
[9]胡维多,SCHEERES D J,向开恒.飞行器近小行星轨道动力学的特点及研究意义[J].天文学进展,2009,27(6):152-166.
[10]ZHANG Zhenjiang,CUI Hutao,REN Gaofeng.Modeling for the gravitation potential environment of an irregular-shaped asteroid and the spherical harmonic coefficient estimation[J].Spacecraft Environment Engineering,2010,27(3):383-388.
[11]SHAO Wei,CUI Pingyuan,CUI Hutao.Physical properties calculation of small body using points triangulations[J].Journal of Harbin Institute of Technology,2010,42(5):687-691.
[12]MITCHELLA D L,HUDSONB R S,OSTROA S J,et al.Shape of asteroid 433 Eros from inversion of goldstone radar doppler spectra[J].Icarus,1998,131(1):4-14.
[13]SHEPARD M K,MARGOT Jean-Luc,CHRISTOPHER Magri,et al.Radar and infrared observations of binary near-Earth Asteroid 2002 CE26[J].Icarus,2006,184(1):198-210.
[14]SHINSUKE A,TADASHI M,NARU H.Mass and local topography measurements of itokawa by hayabusa[J].Science,2006,312(5778):1344-1347.
[15]刘林.航天器轨道理论[M].北京,国防工业出版社,2000:104-106.
[16]LARA M,SCHEERES D J.Stability bounds for three dimensional motion close to asteroids[J].Journal of the Astronautical Sciences,2002,50(4):389-409.
[17]SCHEERES D J,MILLER J K,YEOMANS D K.The orbital dynamics environment of 433 Eros:a case study for future asteroid missions[R].Pasadena:Jet Propulsion Laboratory,2003,42(152):1-26.
[18]SCHEERES D J,HSIAO F Y,VINH N X.Stabilizing motion relative to an unstable orbit:applications to spacecraft formation flight[J].Journal of Guidance,Control,and Dynamics,2003,26(1):62-73.
[19]ZHANG Zhenjiang,CUI Hutao.Orbit dynamics and control in the neighborhood of the asteroid's center point[C]//The 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA 2010).Harbin:[s.n.],2010.
[20]SCHEERES D J.Periodic orbits in rotating second degree and order gravity fields[J].Chinese Journal of Astronomy and Astrophysics,2008,8(1),108-118.
