谐振子密度偏差引起的频率裂解的分析

任顺清，赵洪波

（哈尔滨工业大学空间控制与惯性技术研究中心，150001 哈尔滨，h84b@163.com）

谐振子密度偏差引起的频率裂解的分析

任顺清，赵洪波

（哈尔滨工业大学空间控制与惯性技术研究中心，150001 哈尔滨，h84b@163.com）

为研究半球谐振子密度不均匀引起的频率裂解，首先利用解微分方程的布勃诺夫－加廖尔金法建立了谐振子环向密度分布不均匀的动力学方程，根据动力学方程建立了振动系统的状态方程，进而推导了系统的特征方程，根据特征方程解出了在谐振子存在环向密度不均匀的前提下，振动系统存在的两个二阶固有频率，最后求解了固有频率裂解的表达式.

半球谐振子;密度分布不均匀;频率裂解

当半球谐振子的密度、厚度、品质因数等参数分布不均匀，并存在沿半球谐振子周向的四次谐波时，谐振子的二阶振型将出现两个相互间展成45°的固有轴，沿这两个不同固有轴的二阶弯曲振型对应的固有频率分别达到极大和极小值.两个固有频率差称作频率裂解.文献［1］只给出了频率裂解的公式，并没有给出详细的推导过程.如果对谐振子的激励不沿固有轴方向，频率裂解会使谐振子振型的驻波向固有轴缓慢漂移直至振动沿固有轴方向，从而导致陀螺漂移.本文将针对密度分布不均匀引起的频率裂解进行详细推导，得出与文献［1］不同的更加精确的频率裂解表达式.

1 密度分布不均匀的谐振子动力学方程的推导

如图1所示，半球壳谐振子坐标系为OXYZ，半球壳谐振子中曲面一点的矢径为R，把经线和纬线作为坐标曲线α、β，它们的切线单位矢量e1、e2和法线单位矢量e3组成1个右手局部坐标系.

假设半球壳的中曲面任一点在局部坐标系的位移为M=ue1+ve2+we3.将谐振子各点的位移按不可拉伸薄壳的二阶固有振型展开得

式中:U(α)=V(α)=sinαtan2(α/2)，W(α)=－(2+cosα)tan2(α/2)为二阶固有振型的瑞利函数，p(t)、q(t)为按二阶固有频率振动的位移函数.

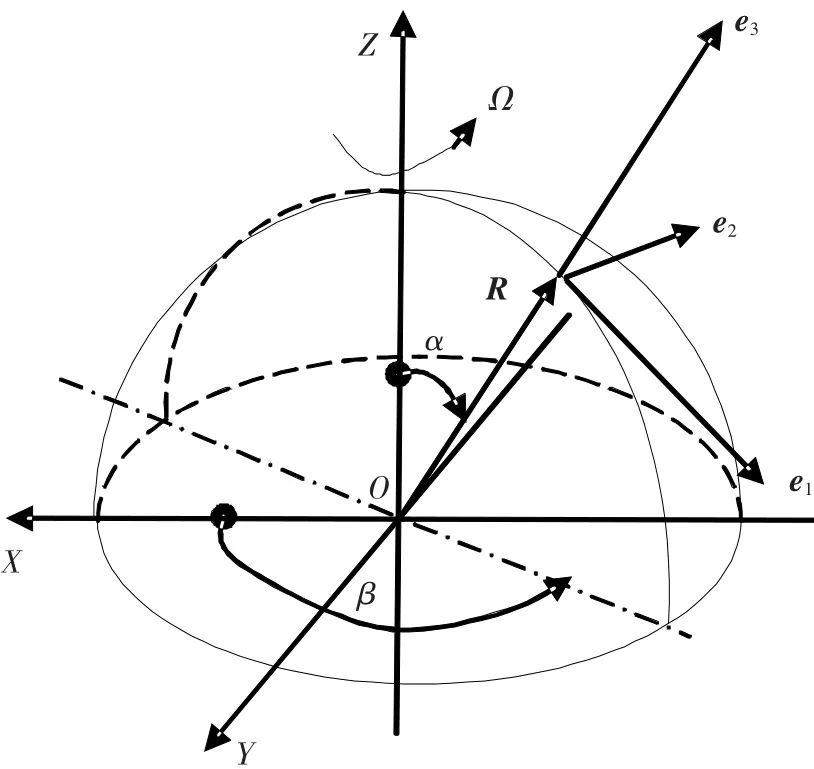
图1 半球谐振子坐标系

由于密度不均匀，将密度ρ沿谐振子周向角β展开成Fourier级数的形式，如下:

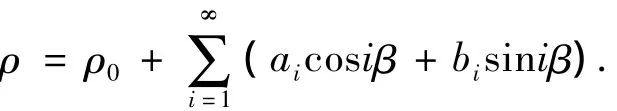
式中ai为密度展开式第i次谐波余弦幅值，bi为密度展开式第i次谐波正弦幅值.

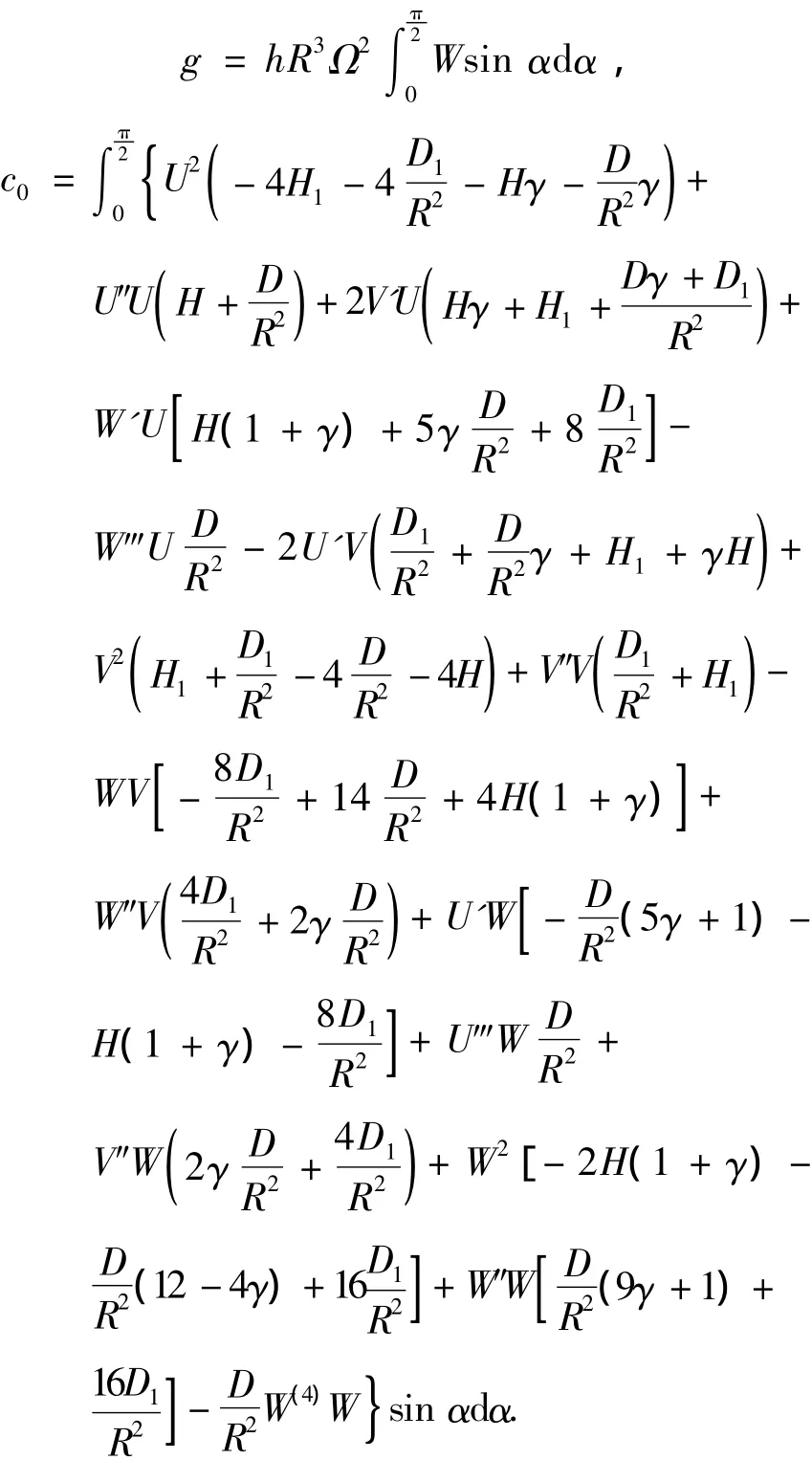
式中:阻尼l=c0/Q，Q为半球谐振子的品质因数;E为杨氏模量;h为半球谐振子薄壳的厚度;γ为半球谐振子材料的泊松比;ω0为不考虑频率裂解时的半球谐振子二阶固有频率;W'、W″、W‴、W(4)表示瑞利函数W对周向角.β求一、二、三、四阶导数，其他类同.

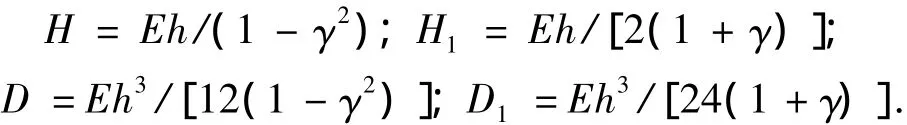
2 频率裂解公式的推导

下面将证明对于动力学方程(1)，有两个二阶固有频率ω1、ω2的存在，本节将推导出固有频率裂解表达式.

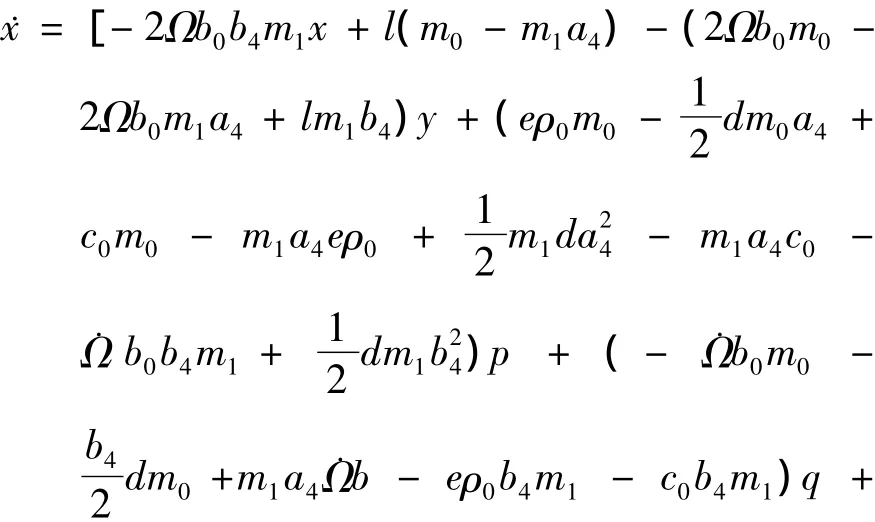
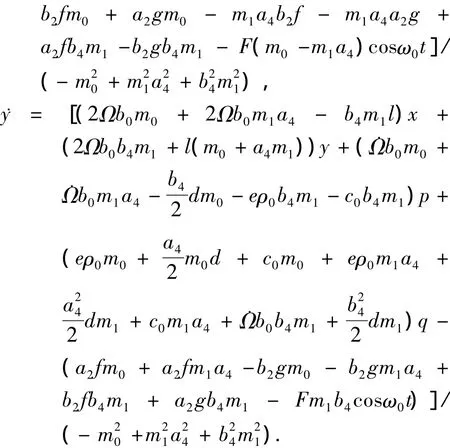
根据以上各式可以建立以振动位移和速度的状态方程为

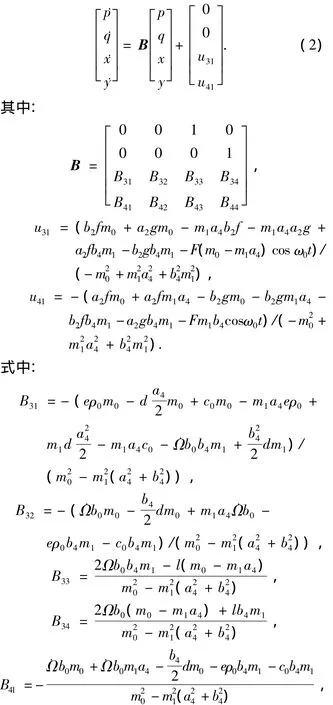
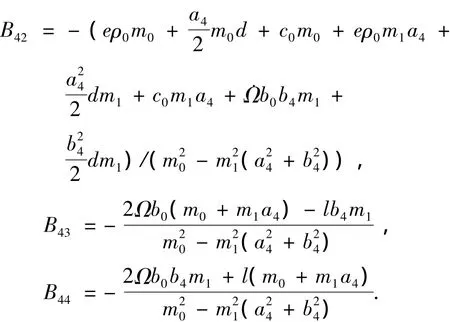
矩阵B的特征方程为

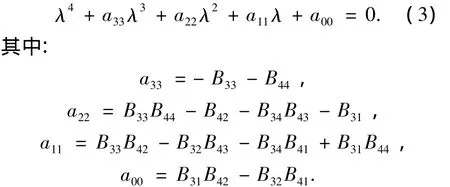
对式(3)进行处理，令λ=s－a33/4得

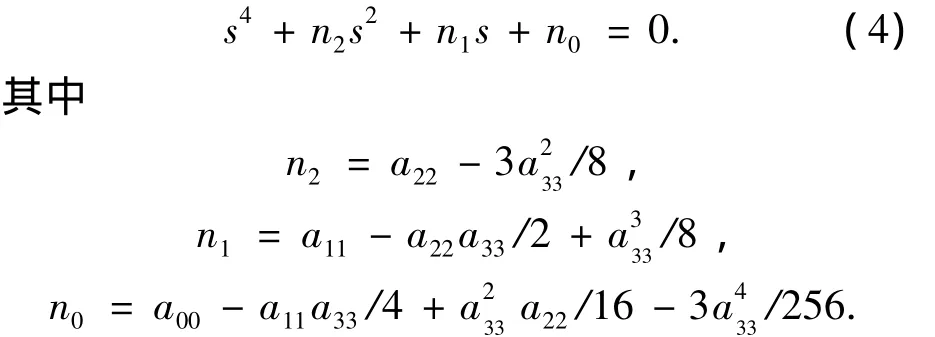
设特征多项式(4)的4个根为

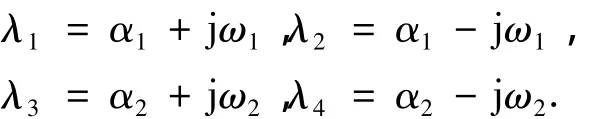
本文第3节将要证明当阻尼l较小时有

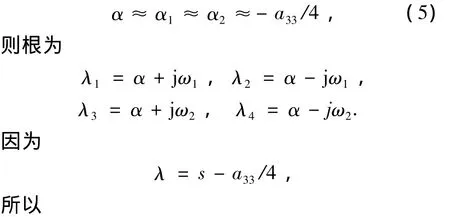
将 s1、s2、s3、s4代入如下方程:

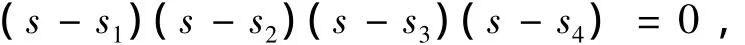
并与式(4)比较得

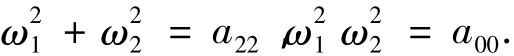
利用韦达定理解一元二次方程并假设ω1＞ω2得

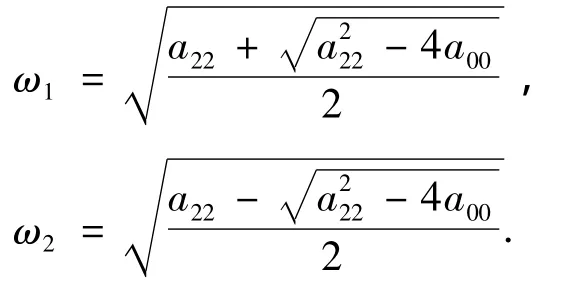
对式(1)中的各参数如m0、m1等进行积分计算，并带入式(2)中B矩阵的各个参数，再计算a00、a22，最后对上式化简得

由于 ε4≪ ρ0，所以

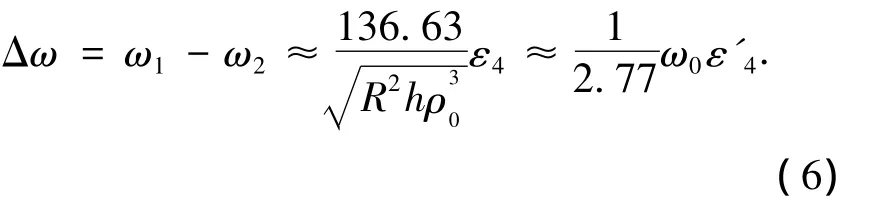
3 品质因数对结果影响的算例验证

公式(5)是在阻尼l较小的假设下推导出来的，阻尼l由品质因数Q决定，因此下面将利用实际数值讨论品质因数Q对公式(6)的影响.

目前国内生产谐振子的材料为熔融石英，其密度ρ=2 200 kg·m－3，杨氏模量 E=7.67×1010N·m－2，泊松比 γ =0.17，中曲面半径R=0.015 m，厚度h=0.85×10－3m，根据文献［2］计算得 ω0=18 727 rad·s－1，现对 a4b4取不同的值进行验证，结果如表1所示.

表1 品质因数对频率裂解的影响

国内某研究所生产的半球谐振子品质因数Q能达到107，因此根据本文的假设推导的公式(5)是正确的.

4 结论

1)在半球谐振子环向密度不均匀的情况下建立了谐振子的动力学方程;

2)根据动力学方程建立了振动位移、速度的状态方程，根据系统的特征方程证明了谐振子在密度不均匀存在四次谐波的情况下，存在两个二阶固有频率;

3)在忽略了谐振子阻尼的情况下，简化了频率裂解的解析表达式.上面的方法在分析谐振子其他缺陷比如厚度、密度、杨氏模量、品质因数不均匀时的频率裂解提供了一种分析方法.

［1］МАТВЕЕВ В А，ЛИПАТНИКОВ В И，АЛЕИН А В.Проектирование. Волнового твердотелъного гироскопа［M］. Москва:Издателъство МГТУ имениН.Э.Баумана，1998:1 －43.

［2］赵洪波，任顺清，李巍.半球谐振子动力学方程的建立及固有频率的计算［J］.哈尔滨工业大学学报，2010，42(11):1702 －1706.

［3］EMILY L B，ALLAN Y L.In-flight characterization of cassini inertial reference units［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Hilton Head，South Carolina:AIAA，2007 －6340.

［4］JIAYI Q，XUE C，SHUNQING R，et al.Dynamic error mechanism analysis of HRG［C］//ISSCAA2008，Shenzhen:［s.n.］，2008:12.

［5］ZHBANOV Y K.Vibration of a hemispherical shell gyro excited by an electrostatic field［J］.Mechanics of Solids，2008，43(3):328 －332.

［6］ZHBANOV Y K，ZHURAVLEV V P.Effect of movability of the resonator center on the operation of a hemispherical resonator gyro［J］.Mechanics of Solids，2007，44(3):851－859.

［7］FAN Shang-chun，LIU Guang-yu，WANG Zhen-jun.On flexural vibration of hemispherical shell［J］.Applied Mathematics and Mechanics，1991，12(10):1023 －1030.

Analysis of frequency cracking of resonator under the density error

REN Shun-qing，ZHAO Hong-bo

(Space Control and Inertial Technology Research Center，Harbin Institute of Technology，150001 Harbin，China，h84b@163.com)

In order to study the frequency cracking caused by the nonuniform of density distribution，the dynamics equations of resonator under the nonuniform of density distribution were established by way of Bubonov—Galerkin method which is common used for solution of differential equations，the state equation was established by the dynamics equations，and then the system characteristic equations were derived.According to the system characteristic equations，two second order natural frequency caused by the density nonuniformity around the hemispherical of vibration system and the expression of frequency cracking were solved.

hemispherical resonator;density distribution nonuniform;frequency cracking

U666.1

A

0367－6234(2012)03－0013－04

2011－01－12.

任顺清(1967—)，男，教授，博士生导师.

(编辑 张 宏)