导航卫星轨道拟合方法与仿真研究
2012-11-15万家欢庄春华陈秀万李智慧张威奕
万家欢,庄春华,陈秀万,李智慧,张威奕
(1.北京大学遥感与地理信息系统研究所,北京100871;2.北京环球信息中心,北京100094;3.92292部队,山东青岛266405)
导航卫星轨道拟合方法与仿真研究
万家欢1,3,庄春华2,陈秀万1,李智慧1,张威奕1
(1.北京大学遥感与地理信息系统研究所,北京100871;2.北京环球信息中心,北京100094;3.92292部队,山东青岛266405)
提出利用虚拟现实技术加强对导航卫星星座的三维仿真模拟,用于系统的设计与监控。考虑到GPS系统的成熟性和与北斗系统的相似性,以GPS精密星历为基础,深入研究利用GPS精密星历拟合卫星三维坐标的方法,对两种常用方法——拉格朗日多项式内插和切比雪夫多项式拟合的处理效果进行分析和比较,给出两种拟合方法得到的卫星位置误差与阶数的关系,探讨短时间外推的效果,确定切比雪夫多项式拟合为最佳的卫星轨道拟合方法,并据此求得任意时刻的卫星坐标,构建了导航卫星三维标准化轨道虚拟运行场景。
精密星历;卫星轨道;拉格朗日多项式;切比雪夫多项式;虚拟现实
一、引 言
在航空航天领域,卫星信息显示、轨道模拟、姿态异常等通常难以用数据形式表达,因此,国外纷纷建立三维仿真系统来研究并监控在轨卫星的运行状态,国内卫星系统仿真还处于使用国外的可视化仿真工具来开发应用程序的阶段,如卫星工具包STK(satellite tool kit)等,这些软件价格昂贵,不公开源代码,且在一些系统分析组件方面对我国用户有很大的限制。鉴于GPS的成熟性和与北斗的相似性,利用虚拟现实技术加强对GPS系统星座的三维仿真模拟及相关分析,对加快我国新一代导航定位系统的发展具有很强的现实意义。
GPS精密星历由国际卫星导航服务(International GNSS Service,IGS)等国际组织发布,它给出了卫星在ITRF中的三维坐标及卫星钟差,其中三维坐标的最终精度为±5 cm,可以满足高精度定位的需要。但GPS精密星历的数据采样间隔一般为15 min,因此在GPS仿真系统三维轨道的生成中,用户需选择合理的数学模型对GPS精密星历进行插值或者拟合,才能获得任意时刻卫星的位置,这是生成虚拟卫星轨道的基础数据[1-5]。
基于GPS精密星历的轨道逼近算法通常采用轨道拟合和坐标内插。其中,内插多以拉格朗日内插为主;拟合多以切比雪夫多项式为主,它们都能实现导航卫星轨道拟合,但拟合精度和拟合效果不同,在实际工程中的可应用性也不同。为了确定工程上可用的最佳卫星轨道拟合方法和达到精度要求的拟合多项式阶数,需构建标准化的三维轨道虚拟运行场景。本文对这两种常用方法的处理效果进行了分析和比较,给出了两种拟合方法得到的卫星位置误差与阶数的关系,并进一步探讨了短时间外推的效果,最终确定了切比雪夫多项式拟合为最佳的卫星轨道拟合方法。本文选用符合精度要求的多项式拟合阶数得到了任意时刻的卫星坐标,在此基础上开发了基于MFC和WTK的单视图导航卫星三维标准化轨道虚拟运行场景。
二、两种拟合方法的数学模型
1.拉格朗日多项式内插[6]
设y=f(x)是区间[a,b]上的一个实函数,xi(i=0,1,…,n)是[a,b]上n+1个互异实数,且y=f(x)在xi的值为yi=f(xi),则区间[a,b]上任意一点x的n阶拉格朗日多项式的代数表达式为
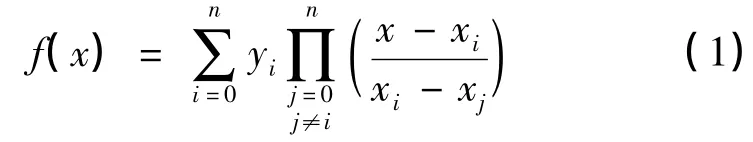
利用n阶拉格朗日多项式内插任意时刻的卫星位置,必须至少有n+1个时刻的卫星位置,并且内插时刻要在已知时刻的区间内。
2.切比雪夫多项式拟合
假设需要在时间间隔[t0,t0+Δt]计算n阶切比雪夫多项式系数(其中,t0为起始历元时刻;Δt为拟合时间区间的长度),先将变量t∈[t0,t0+Δt]变换成τ∈[-1,1]

则卫星坐标(X,Y,Z)的切比雪夫多项式为
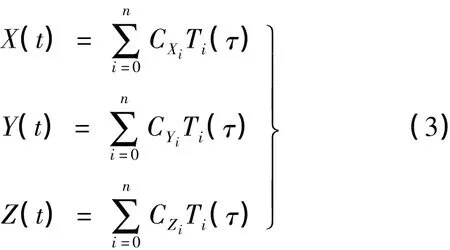
式中,n为切比雪夫多项式的阶数;CXi、CYi、CZi分别为X坐标分量、Y坐标分量、Z坐标分量的切比雪夫多项式系数,为待求量。Ti根据递推公式(2)确定。根据所取时间段内已知的GPS卫星坐标,利用最小二乘法可以计算出某一颗GPS卫星在[t0,t0+Δt]时间区间内的切比雪夫多项式拟合系数CXi、CYi、CZi。利用这些系数,根据式(3)可以计算出[t0,t0+ Δt]时间区间内任意时刻的卫星坐标[7]。
三、精密星历拟合方法分析和比较
在NASA官方网站上下载SP3精密星历文件,本文选取起始历元在2008年5月1日0时0分0秒,终止历元时刻在2008年5月1日23时45分0秒的SP3精密星历文件作为试验数据。
1.拉格朗日内插效果分析
本文选用卫星序号为11的历元值作为试验数据,取拟合的时间间隔为30 min,采用对称内插的方法,取30 min间隔的历元作为内插点计算各个内插时间段中间时刻的卫星位置,以便将内插得到的卫星位置同精密星历给出的卫星位置进行比较。根据以上分析,利用VC6.0软件编写相应程序,得到了11号卫星5~18阶的内插结果(表1给出了8~18阶的内插结果)。
由表1可知,随着阶数逐渐升高,拉格朗日插值误差逐渐减小。阶数为12阶时,X、Y、Z 3个坐标的最大中误差为±2.40 mm,最大误差为6.05 mm,内插的结果满足精密定位的要求。当阶数高于12阶时,插值精度基本不变。用同样的方法内插序号为4、21两颗卫星坐标,与11号卫星坐标内插结果进行比较,并利用Matlab软件绘制出中误差变化趋势图(如图1所示)。图1给出了卫星序号为4、11、21这3颗卫星5~18阶插值的点位中误差变化趋势图,其中图1(a)为5~18阶变化全图,图1(b)为局部放大图。由图1可以看出,用30 min内插计算的3颗卫星轨道的精度变化趋势是一致的,随着内插阶数的增加,内插精度逐渐升高,精度最终稳定在±2 mm左右。

表1 拉格朗日内插结果对比表 mm

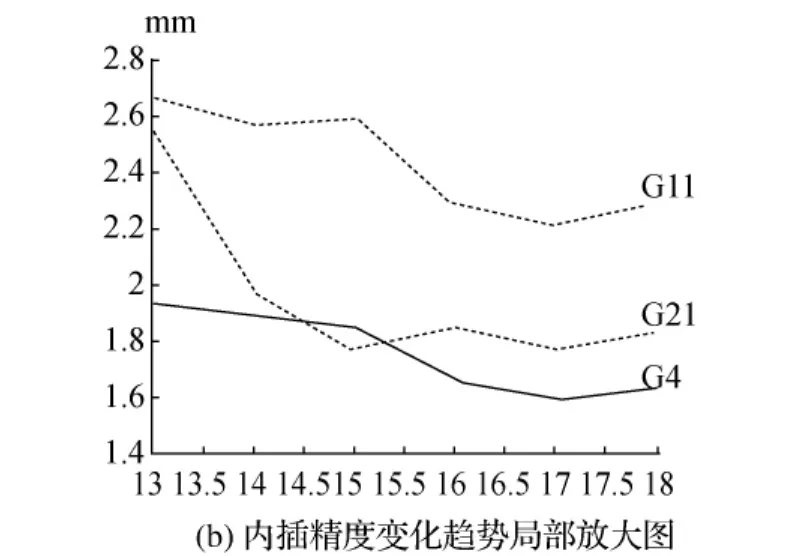
图1 内插精度变化趋势图
2.切比雪夫多项式多项式拟合效果分析
在切比雪夫多项式拟合中,输入的拟合参数有两个:拟合阶数和拟合时间段长度,下面分别探讨这两个参数对拟合结果的影响。
取拟合时间段为4 h,选用序号为4的卫星历元值作为试验数据,不同阶数的切比雪夫多项式拟合结果如表2所示。
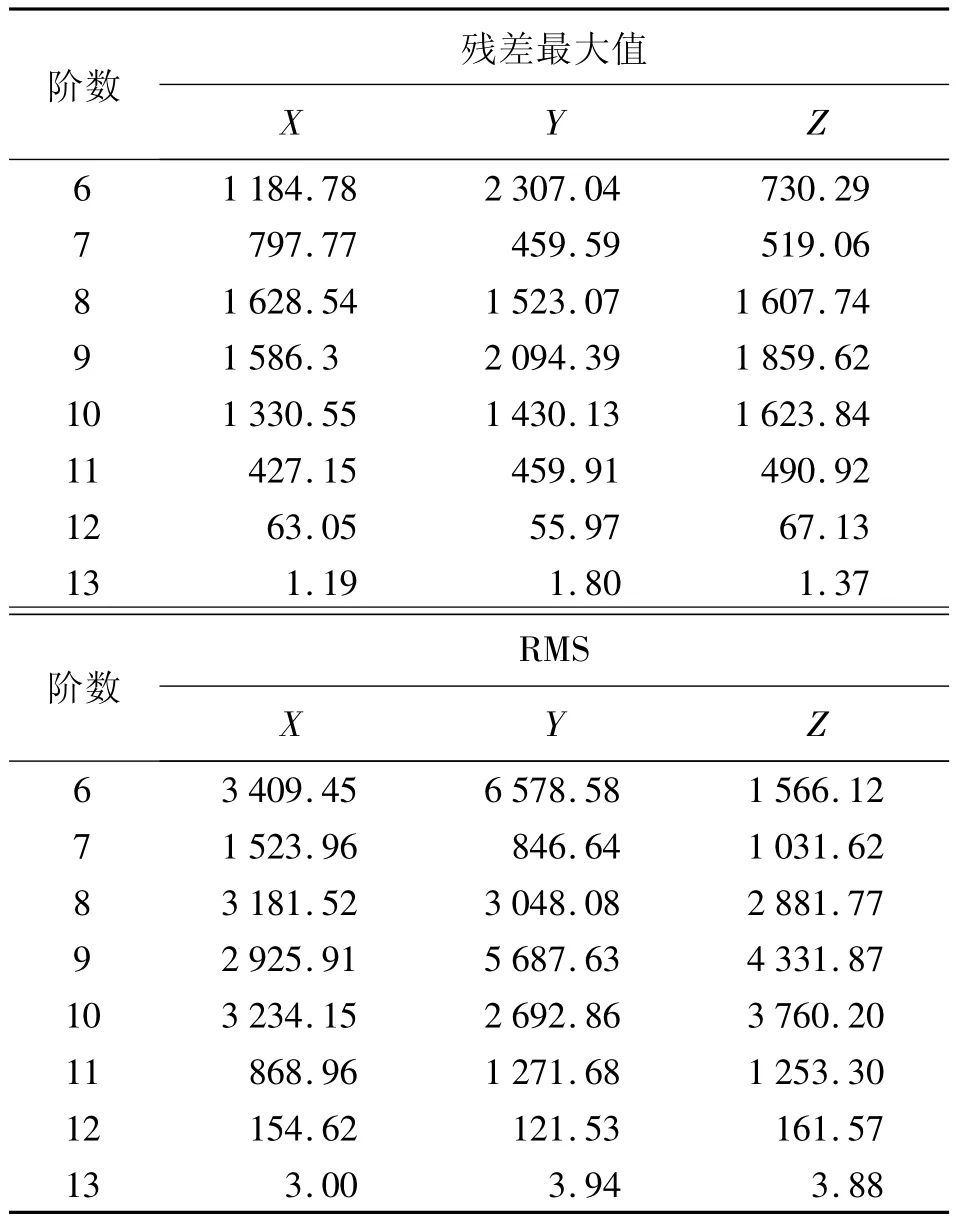
表2 切比雪夫多项式拟合结果对比表 mm
由表2可以得出在一定时间间隔内,切比雪夫多项式的阶数取得越高,拟合的数据精度越高,阶数取13时,可以达到毫米级的精度。但是在时间段取为4 h时,该时间段内的精密星历历元数为16,根据切比雪夫多项式拟合的数学原理可知,在该时间段内阶数最多只能取到13阶,这就说明在短时间弧段内,拟合阶数受到历元数的限制,难以通过增加拟合阶数来提高拟合的精度。
取不同的时间段,并且将该时间段内所有的历元数据全部作为已知数据参与拟合,拟合的结果如表3所示。
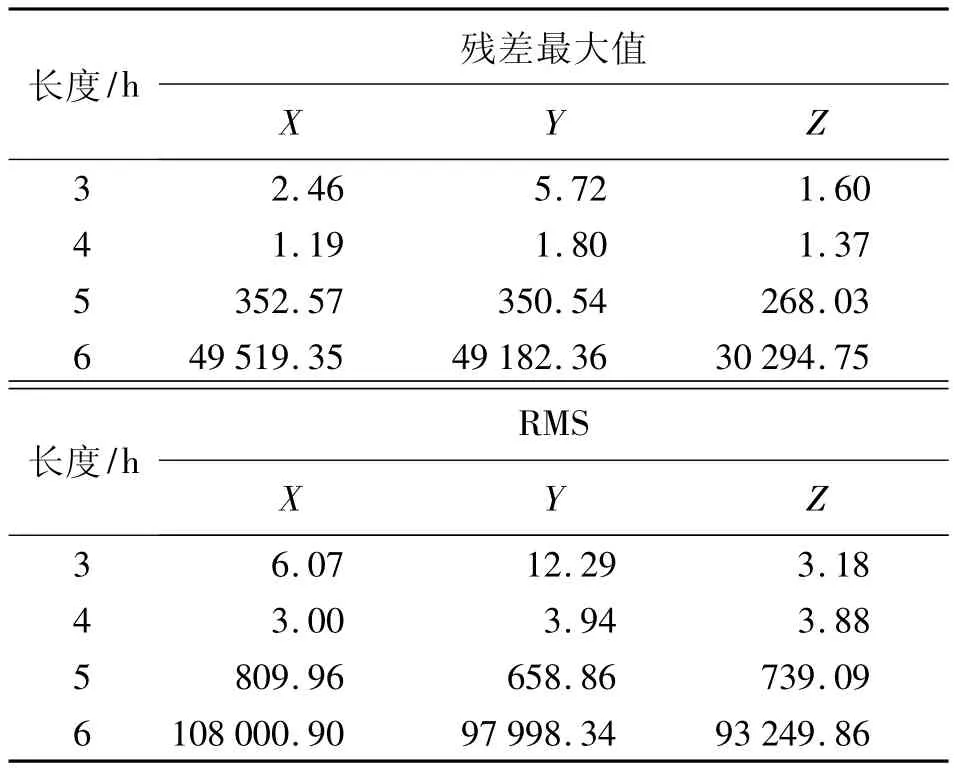
表3 不同时间段拟合结果对比表 mm
由表3可以看出,所取的拟合时间间隔越长,拟合的精度越差,在拟合时间段超过5 h以后,拟合的精度显著下降。原因是IGS精密星历提供的历元时间间隔为15 min,处于15 min之间的时刻没有卫星数据,而时间段越长所选用的离散数据点相关性越差,影响到切比雪夫多项式的拟合精度。
由于IGS精密星历给出的最后一个历元时刻为23时45分0秒,而在实际应用中,有时需要使用23时45分0秒至24时0分0秒之间的卫星坐标数据,因此需要利用该时段之前的历元数据来进行外推。根据切比雪夫多项式的数学原理可知,切比雪夫多项式可以对拟合时段之外的数据进行外推,下面探讨对IGS精密星历外推的效果。
取时间段为4 h,阶数为12对第4颗卫星的轨道进行拟合,得到一个时间段内16个历元的残差分布表(如表4所示)。
由表4可以看出,16号历元的残差明显大于其他历元,它的残差为分米级,而其他历元的残差为厘米级。因为16号历元在拟合的时间段外,属于外推范围。由于IGS精密星历的历元时间间隔较大,外推的卫星轨道与实际轨道相差较远,因此残差也比较大。所以在利用切比雪夫多项式拟合精密星历时,如果对拟合数据精度要求不高,可以利用切比雪夫多项式进行有限的外推;如对拟合数据精度要求较高,如精密单点定位,则需要将所需时刻纳入到拟合的时间段之内。
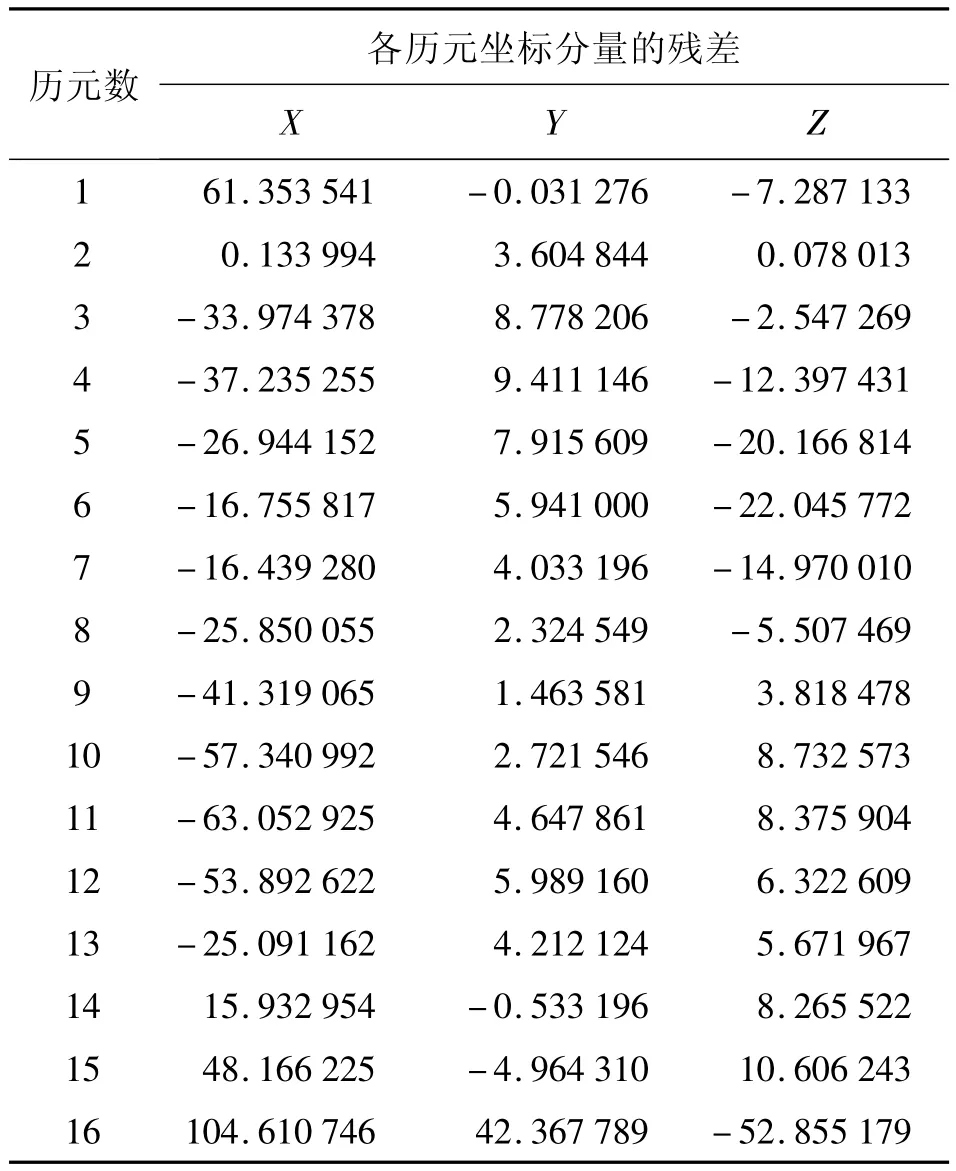
表4 前16个历元的残差分布表 mm
3.两种数学模型处理效果比较
本文选用11号卫星的历元值作为试验数据,并比较了两种数学模型处理的效果。图2给出了阶数为16的拉格朗日内插后的X坐标分量的残差分布图;图3给出了阶数为13、时间段长度为4 h的切比雪夫多项式拟合后X坐标分量的残差分布图。
由图2可知,16阶拉格朗日内插后的X坐标分量的最大误差为2.8 mm左右;由图3可知,13阶切比雪夫多项式拟合的X坐标分量最大误差为1.6 mm左右,且拉格朗日内插的出的数据比切比雪夫多项式拟合出的数据误差波动的范围要大一些。

图2 16阶拉格朗日内插残差分布图
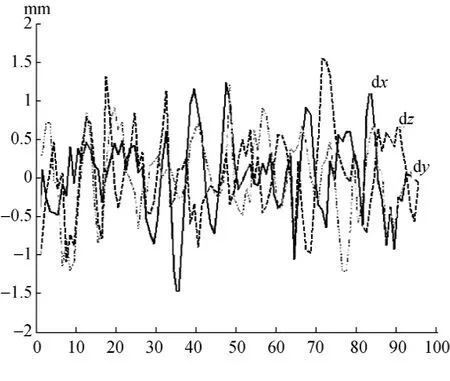
图3 13阶切比雪夫多项式拟合残差分布图
另外,通过对两种数学模型表达式(1)和式(3)分析比较后得出,利用切比雪夫多项式拟合卫星轨道易计算,占用的计算机内存小,并且可外推出拟合时间段以外时刻的卫星坐标,其精度完全满足导航卫星轨道拟合的要求。因此,确定切比雪夫多项式拟合为最佳的卫星轨道拟合方法,并选用阶数为13,时间段长度为4 h的切比雪夫多项式进行坐标拟合。
四、虚拟卫星轨道的生成
SP3精密星历是地心地固坐标系下给出的卫星位置轨道数据,而在进行虚拟仿真时,为了表达地球自转,卫星轨道数据应转化到天固坐标系中。SP3精密星历的历元间隔为15 min,随着历元的递增,地球转过的角度也递增,将地固坐标系下坐标转化到天固坐标系时,相应的旋转角度也递增,递增的步长大小就是15 min内地球转过的角度,因此通过将不同历元的卫星坐标按照其对应的自转角度进行转换,就可得到天固坐标系下卫星的运动轨迹。为了验证此方法的正确性,本文通过Matlab,对所采用的设计思路进行了仿真验证。在不考虑地固坐标系在天固坐标系中初始定向的情况下,以IGS发布的2008年5月1日0时0分0秒的SP3星历为例进行坐标变换,变换前后卫星轨迹如图4所示。
其中,图4(a)表示的是地固坐标系下的轨道坐标直接在天固坐标系下形成的卫星轨迹,画出的是一个封闭的马鞍线,图4(b)表示的是经过坐标转换后天固坐标系下的卫星轨迹;图4(c)表示地固坐标系下的轨迹在天固坐标系下画出的所有GPS卫星轨迹;图4(d)表示经坐标转换后的天固坐标系下的轨迹分布。可以看出,卫星大致分布在6个轨道平面内,符合GPS实际空间分布情况。
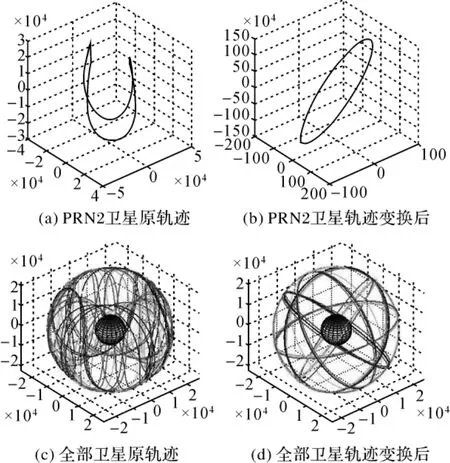
图4 变换前后卫星轨迹
根据切比雪夫多项式拟合原理和分析比较结果,由式(3)对IGS发布的2008年5月1日SP3星历进行计算,得到任意时刻的卫星位置数据。然后,在基于MFC和WTK的单文档GPS卫星仿真系统中通过调用WTK的API函数动态渲染生成虚拟运行场景,实现效果如图5所示。
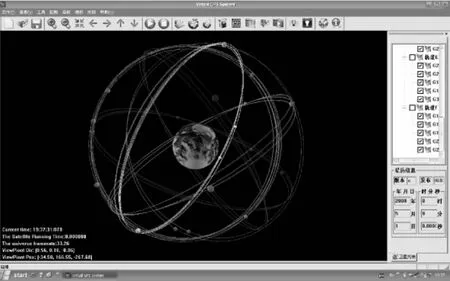
图5 GPS卫星仿真系统运行界面
五、结束语
本文深入研究了利用GPS精密星历拟合卫星三维坐标的方法。对拉格朗日多项式内插和切比雪夫多项式拟合的处理效果进行了分析和比较,给出了两种拟合方法卫星位置误差与阶数的关系,确定了切比雪夫多项式拟合为最佳的卫星轨道拟合方法,并在虚拟环境中进行了验证与实现,提高了卫星导航系统模拟仿真的精度,为我国北斗导航定位系统建设中卫星轨道的设计明确了计算方法,为我国卫星轨道虚拟仿真提供了参考。
[1] 蔡艳辉,程鹏飞,李夕银.卫星坐标的内插和拟合[J].全球定位系统,2003,27(3):10-13.
[2] 张守建,李建成,邢乐林,等.两种IGS精密星历插值方法的比较分析[J].大地测量与地球动力学,2007,33(2):80-83.
[3] 王义峰,文鸿雁,刘立龙.用切比雪夫多项式标准化GPS卫星轨道[J].测绘与空间地理信息,2008,31(1):21-23.
[4] 陈兆林,张书毕,佟瑞菊.用拉格朗日多项式内插计算GPS卫星位置[J].全球定位系统,2007,33(2): 33-35.
[5] FENG Yanming,ZHENG Yi,BAI Zhengdong.Representing GPS Orbits and Corrections Efficiently for Precise Wide Area Positioning[C]∥Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GNSS2004.California:[s.n.],2004.
[6] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005:33-37.
[7] 孔巧丽.用切贝雪夫多项式拟合 GPS卫星精密坐标[J].测绘通报,2006(8):1-3.
[8] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003:102-104,118.
Research on the Orbit Fitting Methods of Navigation Satellite and Simulation Realization
WAN Jiahuan,ZHUANG Chunhua,CHEN Xiuwan,LI Zhihui,ZHANG Weiyi
0494-0911(2012)07-0001-05
P228.4
B
2011-07-07
国家国防科技工业局民用航天预研项目
万家欢(1986—),男,湖北浠水人,硕士,主要从事卫星导航应用方面的研究工作。
