方形网格上的Stieltijes型混合有理插值

陈艳秋， 王家正

（1.安徽大学数学科学学院，安徽合肥 2300601；2.合肥师范学院数学系，安徽合肥 2300601）

方形网格上的Stieltijes型混合有理插值

陈艳秋1， 王家正2

（1.安徽大学数学科学学院，安徽合肥 2300601；2.合肥师范学院数学系，安徽合肥 2300601）

文章基于Stieltijes型分叉连分式有理插值，结合Thiele型连分式及Newton多项式，构造了一种方形网格上的二元混合有理插值函数，通过定义偏差商、偏逆差商和混合逆差商建立递推算法。构造的这种有理插值函数满足有理插值问题中所给的插值条件，并给出了插值的特征定理及其证明，进行了误差分析，最后给出的数值例子，验证了所给算法的有效性。

连分式；有理插值；特征定理；误差分析

1 引言

对称型的连分式插值是由［1］、［2］A.Cuyt、B.Verdonk，［3］J.A.Murphy和M.R.O’Donohoe等人于上世纪八十年代中期提出的一种二元连分式插值格式。文［4］将Thiele型有理插值与Newton多项式插值结合起来构造一种混合有理插值，并给出了相应的性质。［5］、［6］分别构造了不同形式的对称型混合有理插值格式。本文基于Stieltijes型分叉连分式，定义偏差商、偏逆差商和混合逆差商建立递推算法，构造了一种新的方形网格上的二元混合有理插值函数，所得的这种有理插值函数满足有理插值问题中所给的插值条件，并给出了插值的特征定理及其证明，进行了误差分析，最后给出的数值例子，验证了所给算法的有效性。

2 二元混合有理插值

2.1 二元混合有理插值函数的构造

将Stieltijes型分叉连分式与Thiele型有理插值及Newton多项式结合起来构造如下形式的有理函数。

定义2 设有如下形式的有理函数：

其中（x i，y j）∈＝｛（x i，y j，j＝0，1，…，n｝，f（x，y）是定义在包含的区域D＝（a，b）×（c，d）上的二元函数，使R（x i，y j）＝f（x i，y j）＝f i，j，（x i，y j）∈，则称有理函数（1）为二元函数f（x，y）在方形网格上的Stieltijes型混合有理插值函数。

从定义2可以看出，确定f（x，y）的Stieltijes型混合有理插值的关键是确定系数Bi，j，（i，j＝0，1…n），为此我们构造如下的递推算法。

定义3

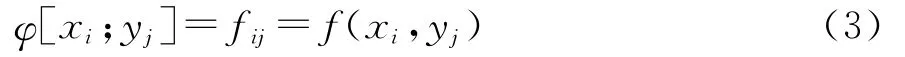
2.2 插值定理

由上面定义的递推算法（3）～（8），可得下面的插值定理：

定理1：对于i，j＝0，1，2，…，n，设Bij＝φ［x0，x1，…，x i；y0，y1，…，y j］，并假设所定义的差商、逆差商和混合逆差商都存在且不为0，则由（1）、（2）定义的R（x，y）满足：R（x s，y t）＝f（x s，yt），（x s，y t）∈

证：不妨设s≤t

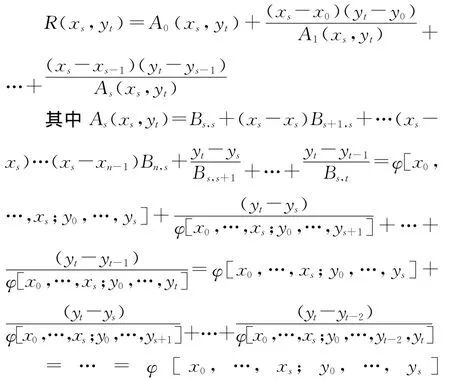
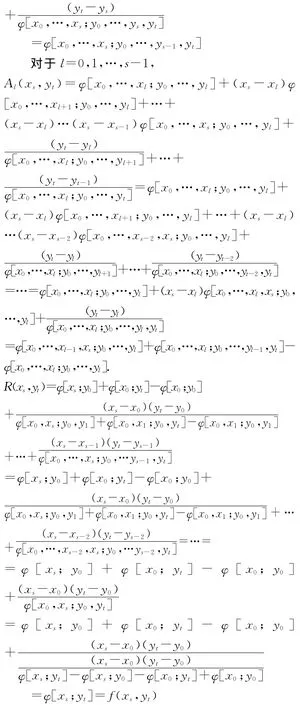
同理可证明当t≤s时结论成立。

3 特征定理及误差分析

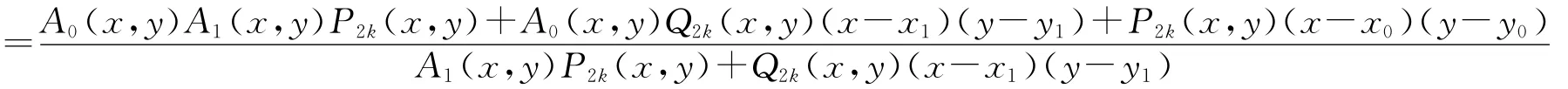
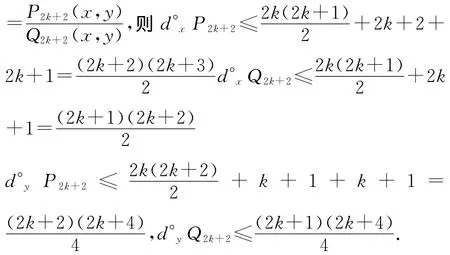
故当n＝2k＋2时，结论也成立.故（1）得证。同理可证（2）成立。

故特征定理得证。

此定理的证明可根据牛顿插值理论证得，这里不再证明。

4 数值例子

例：设f（x，y）在上的初始数据如下表：

f（xi，yj） y0＝0 y1＝1 y2＝2 x0＝0 2 3 2 4 3 x1＝1 5 7 2 3 x2＝2 16 21 2 26 3

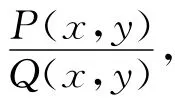
，使之满足插值条件R（x i，y j）＝f（x i，y j）（i，j＝0，1，2）

解 利用差商、逆差商和混合逆差商的递推算法（3）～（8）式，列表计算如下：

表1

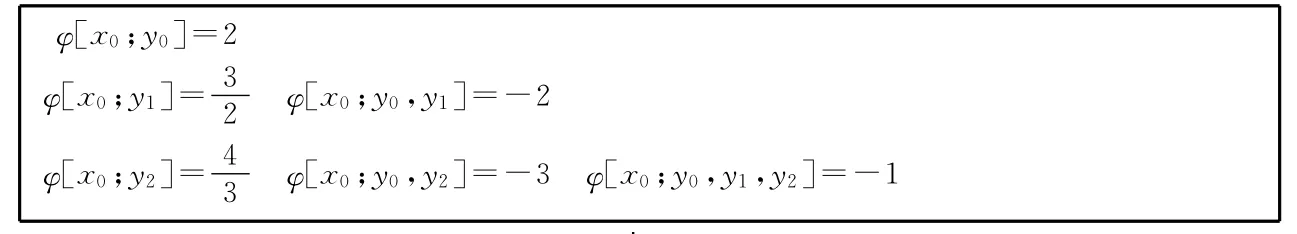
表2

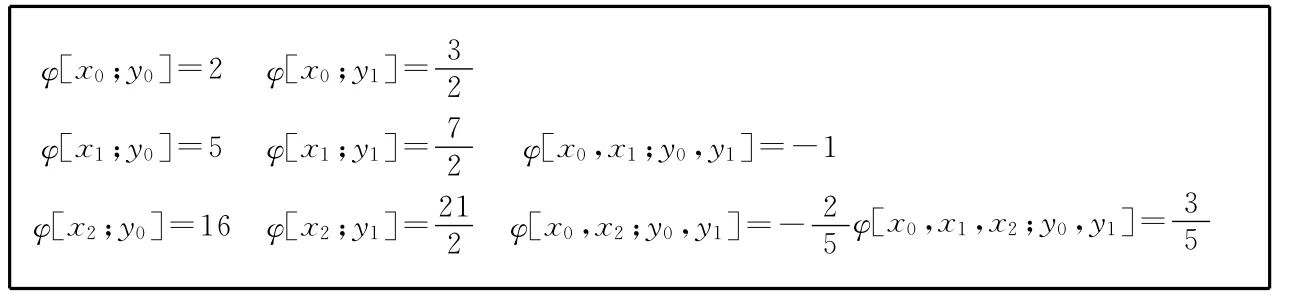
表3

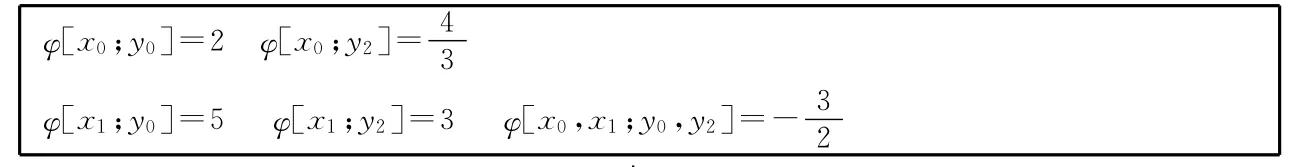
表4

表5

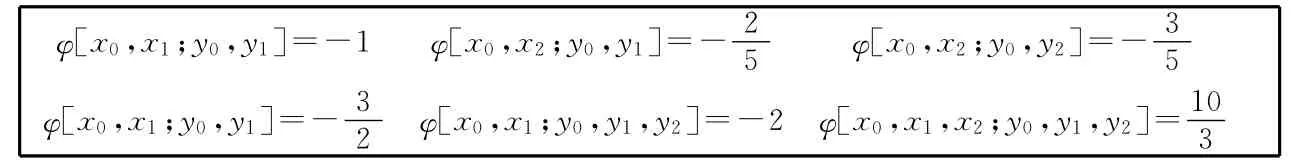
表6

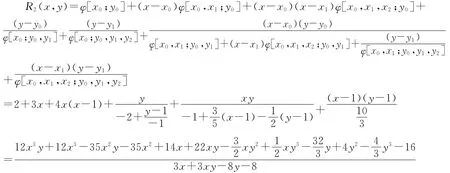
容易验证R（x，y）满足所给的插值条件，并且符合特征定理的结论。

5 结束语

本文通过定义偏差商、偏逆差商和混合逆差商构造了方形网格上的一种新的有理插值格式，并研究了插值函数的特征定理，分析了误差，丰富了连分式理论。当然本文的结果也可以推广到二元向量值和矩阵值有理插值的情形。

［1］ A.Cuyt and B.Verdonk，Multivariate rational interpolation，Computing 1985（34）41－61.

［2］ A.Cuyt and B.Verdonk，Multivariate reciprocal differences for branched thiele continued fraction expansions［J］.J.Comput.Appl.Math，1988，21：145－160.

［3］ J.A.Murphy，M.R.O，Donohoe，A Two－variable generalization of the stieltjes－type continued fraction［J］.J.Comput.Appl.Math，1978，4（3）：181－190.

［4］ Jieqing Tan and Yi Fang Newton－Thiele’s rational inter Polants，Numevical Algorithms 24（2000）：141－157.

［5］ 王家正.Stieltijes—Newton型有理插值［J］.应用数学与计算数学学报，2006，20（2）：15－22.

［6］ 唐烁，郑涛，郑永明.Stieltijes－Thiele型有理插值公式［J］.鲁东大学学报（自然科学版），2010，26（2）：100－105.

Stieltijes’Blending Rational Interpolation on Square Grid

CHEN Yan－qiu1， WANG Jia－zheng2
（1.SchoolofMathematicalScience，AnhuiUniversity，Hefei230061，China；2.DepartmentofMathematics，HefeiNormalUniversity，Hefei230061，China）

In this paper，bivariate blending rational interpolation function was constructed based on stieltijes’branched continued fraction，Thiele rational interpolation and Newton polynomial.By defining the partial difference，the partial inverse difference and blending inverse difference building the recursive algorithm.The bivariate rational function which interpolates the given support points，and interpolating characteristic theorem and its proof is given，also error analysis..Numerical examples are given to show the effectiveness of the result.

continued fraction；rational interpolation；characteristic theorem；error analysis

O241.3

A

1674－2273（2012）03－0001－05

2012－01－20

安徽省教育厅自然科学基金，KJ2011Z300

陈艳秋（1987－），女，安徽大学数学科学学院硕士生，研究方向为数值逼近；王家正（1964－），男，合肥师范学院数学系教授，研究方向为数值逼近。