基于经验模态分解的HHT变换解析洪水频域特性
2012-11-14汪丽娜陈晓宏
汪丽娜, 李 艳, 陈晓宏
(1. 华南师范大学地理科学学院,广东广州 510631; 2. 广东商学院资源与环境学院,广东广州 510320;3. 中山大学水资源与环境研究中心,广东广州 510275; 4. 华南地区水循环与水安全广东省教育厅重点实验室,广东广州 510275)
基于经验模态分解的HHT变换解析洪水频域特性
汪丽娜1*, 李 艳2, 陈晓宏3,4
(1. 华南师范大学地理科学学院,广东广州 510631; 2. 广东商学院资源与环境学院,广东广州 510320;3. 中山大学水资源与环境研究中心,广东广州 510275; 4. 华南地区水循环与水安全广东省教育厅重点实验室,广东广州 510275)
依据经验模态分解的希尔伯特黄变换方法,解析洪水过程的频域特性.以武江流域为研究对象,选取6场洪水过程进行分析.结果表明6场洪水在整个洪水过程中,洪水时间序列的能量主要集中在0.1 Hz以内.洪水时间序列具有多能量组分的特点.EMD分解出的分量具有较清晰的物理意义和自适应性;由于采用三次样条插值来获得信号的瞬时平均值,导致Hilbert-Huang变换得到的结果会出现端点飞翼现象.
经验模态分解; 希尔伯特黄变换; 洪水; 频域特性
洪水时间序列受天气系统的影响,而天气系统具有局地特征,存在多层次时间结构,因此洪水时间序列是多时间尺度系统.加上人类活动的影响,如水库、大坝的修建、城市化的作用,河道下垫面和流域植被的人为改造等,使得洪水时间出现跳跃性的成分,加剧了洪水时间序列的非平稳性.
HHT方法是1996年由美籍华人HUANG等[1]提出的信号时频分析的一种全新方法,采用HHT变换,主要分为经验模态分解(EMD分解)和Hilbert变换.其中EMD分解基于信号的局部特征时间尺度,可以将任意信号分解为少量IMF分量的组合,而且IMF分量能对瞬时频率给出有意义的物理解释[2].之后,对每个分量作希尔伯特变换,刻画出信号的瞬时频率,即保证信号经希尔波特变换后具有清晰的瞬时振幅和瞬时频率意义.该方法非常适于对非平稳、非线性信号进行分析[3].地震工程、海洋工程、医学、语音、图像分析和处理、气象、水文等学科[4-9]也越来越多地采用了HHT的方法进行研究.洪水作为复杂的自然现象,其时间序列具有复杂性和多尺度性.因此,对于洪水时间序列的研究仅停留在时域层面上是不够的,需进一步探究洪水时间序列的频域特性,本研究采用HHT的时频分析法对洪水时间序列进行分析,将洪水时间序列在各时间段的不同分量的能量值显示出来,解析洪水时间序列的时域和频域特性.
1 研究方法
EMD分解通过不同的尺度把信号分解成一系列固有模态函数,由信号的自适应基分解出信号的IMF.每个IMF 只包含单模态的振动,即只有单组分的波组成.这种IMF非常适合Hilbert变换,利用它求出有明确物理意义的瞬时频率.但是,现实中的数据是复杂的,必须要通过分解形成IMF,其分解过程可以参见文献[10].
进行EMD分解的主要目的是进行Hilbert变换,得到Hilbert谱.基于IMF分量的Hilbert谱是一个三维(时间-频率-局部振幅) 谱形,通常可用三维图形或二维图像表示.Hilbert-Huang变换是一种新的具有自适应特性的时频分析方法, 对时变信号在时频平面上随频率和时间变化的规律进行精确的描述, 是信号能量的一种完整的时-频分布[11].
2 结果与分析
根据经验模态分解和Hilbert-Huang变换原理,以武江流域的洪水为例,选取1959、1967、1975、1981、1994和2006年的洪水过程,以年洪峰流量过程作为分析数据,对上述6场洪水的时间序列进行EMD分解,得到IMF分量和HHT谱图(图1),图中原始序列的单位为:m3/s.
图1表明,对1959年的洪水时间序列分解后得到4个IMF分量,对1967、1975、1981、1994和2006年的洪水时间序列进行EMD分解分别得到3、2、3、4和3个IMF分量.图1A中的(a)为洪水时间序列过程图,图1A中的(b)都代表一阶IMF序列,是最先被分解出来的信号.图1B是图1A中的IMF1-IMFi 经过Hilbert变换得到的时频谱值图.为了能清楚地看到洪水时间序列随时频演化的过程,采用了频率-时间-震幅图表示能量变换特征的时频演化过程(图1B).图1B中横坐标为时间,纵坐标为频率,各点表示能量.各IMF分量的瞬时频率是一个围绕中心频率上下波动的量,互相之间的交叉重叠项很少.由Hilbert-Huang变换的图谱得知:洪水时间序列具有明显的随机性和复杂性,但其随机性只局限于一定的范围之内,复杂性中也会有相对主要的成分.
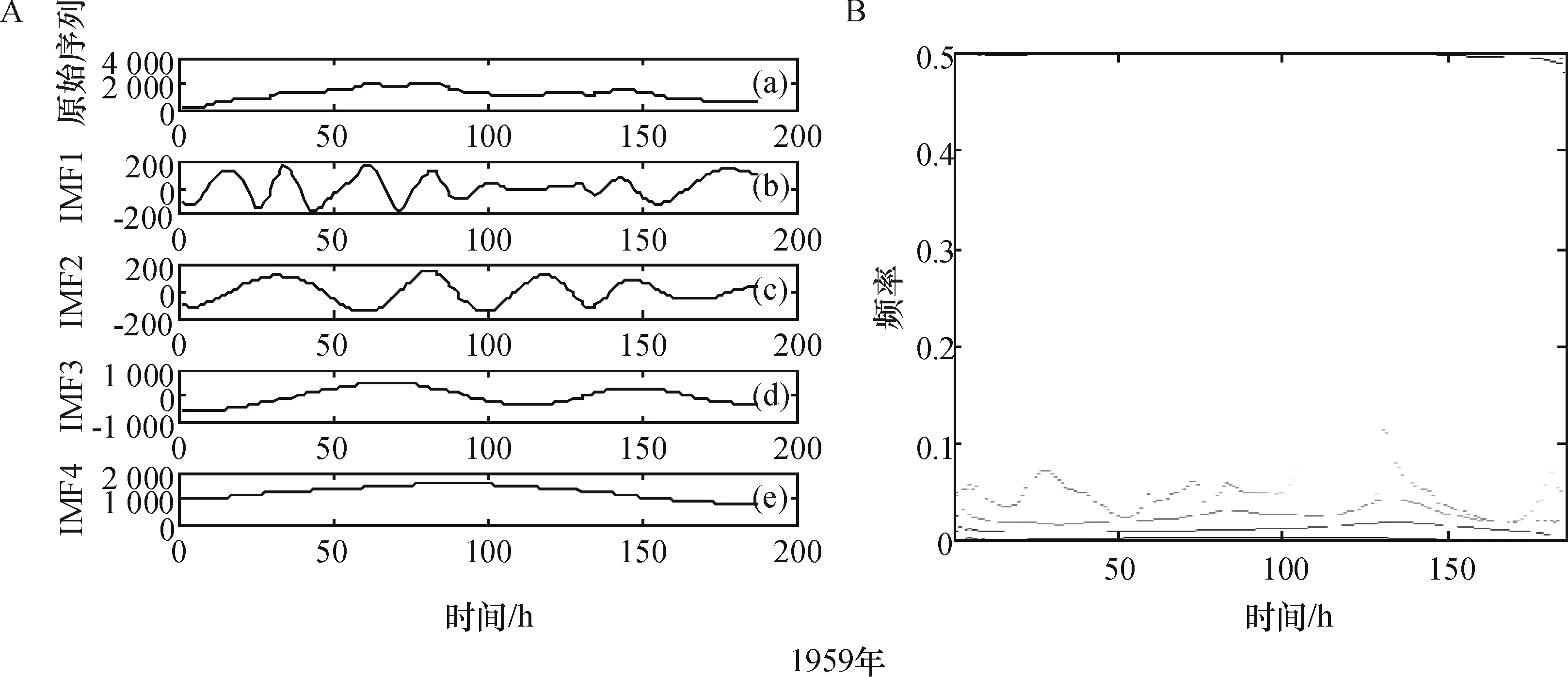
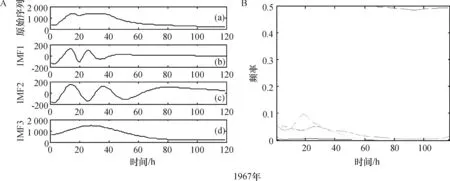
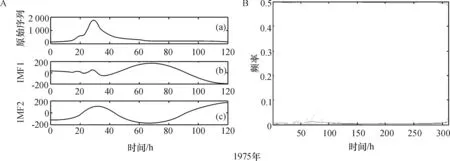
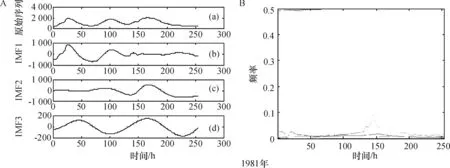
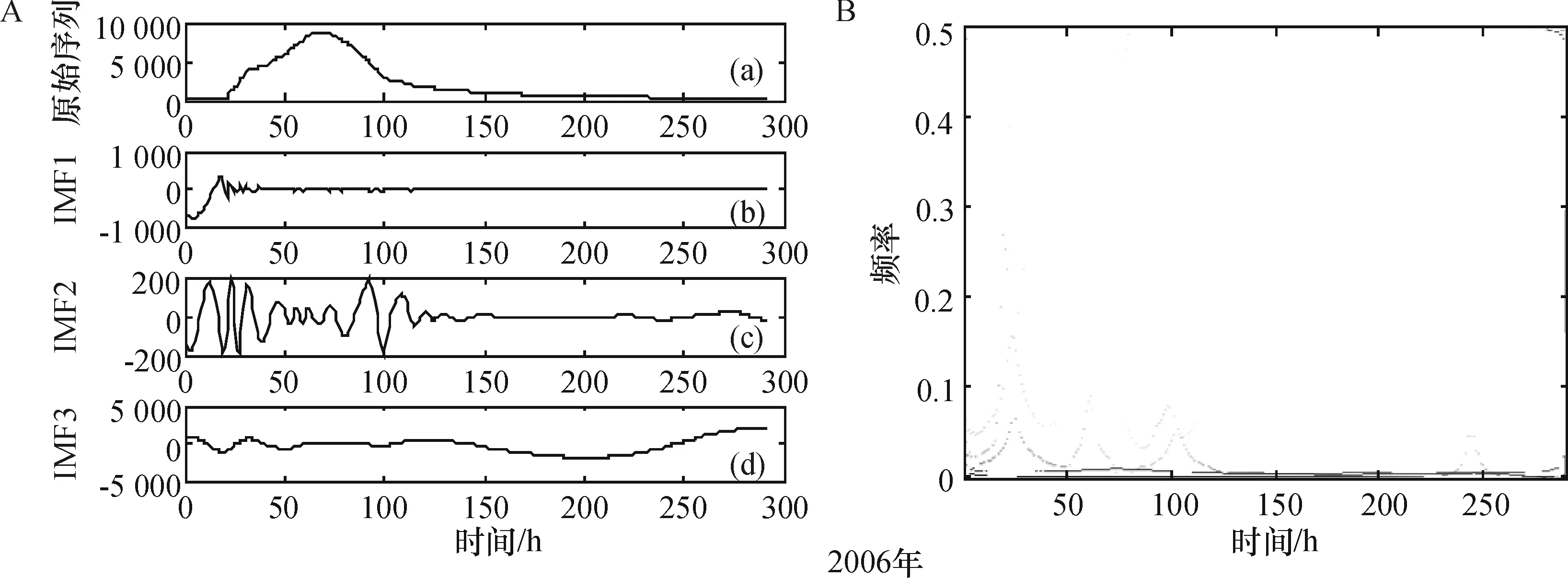
(A)洪水时间序列的EMD分解;(B)洪水时间序列的Hilbert能量谱
EMD分解具有把复杂信号中蕴涵的各种本征波动模式分解出来的功能,通过EMD分解,获得洪水时间序列的各个组分的幅值大小、周期变化及相位信息.将得到的各模态函数进行Hilbert变换,可以获取洪水时间序列的幅值和频率随时间变化的特性.6场洪水的Hilbert能量谱清晰而详细地显示了能量随时频的具体分布;瞬时能量谱更直观地表明了高频能量主要集中在频率值小于0.1 Hz以内的范围.并且每场洪水都显示出,在各时间段内,洪水时间序列具有多能量组分的特点.
由于IMF各分量所包含的信息从高频到低频的成分,每一段频率所包含的频率成分都是不不同的,且随信号本身的变化而变化.本文进一步解析,各IMF分量及其Hilbert变换结果见表1所示.
表1说明,1959年的IMF1到IMF4模态的中心频率分别是0.050 3 a-1、0.025 8 a-1、0.018 6 a-1和0.143 2 a-1,其中IMF1表示为20 a左右的震荡,IMF2表示38~39 a左右的变率,IMF3表示约53 a的波动,IMF4表示约为7 a左右的洪水变化量;就不同的IMF分量来看,除IMF4分量外,1959年其他分量随着振幅的增加,频率减小.其他年份的IMFi分量的统计特征值见表1,对于1981年洪水时间序列,就不同模态的振幅变化看,频率越高,振幅越大.
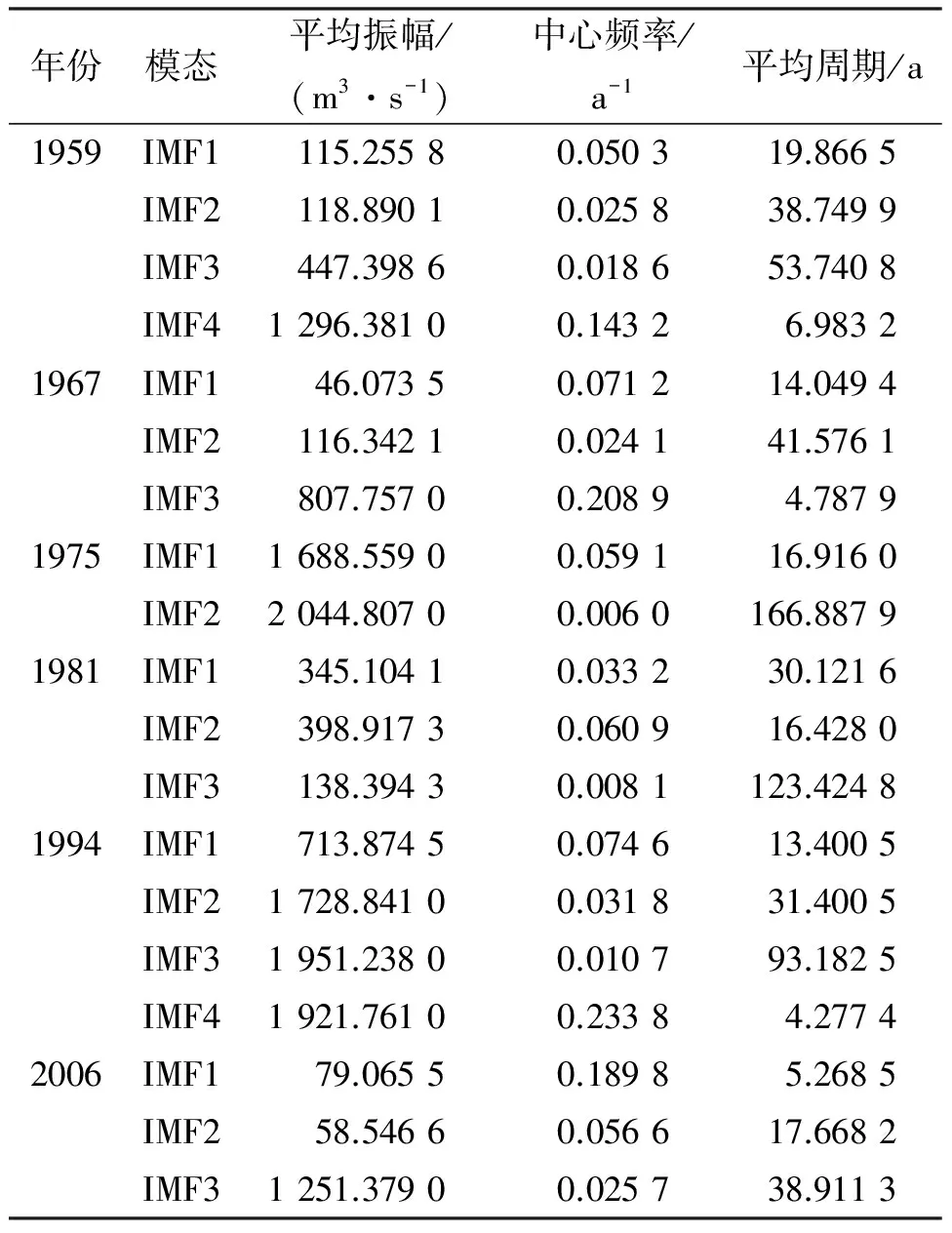
表1 洪水时间序列Hilbert变换后的统计特征值Table 1 Statistics of IMF of flood series transformed by HHT
HHT变换在对洪水时间序列进行分析时,在时域和频域均具有较好的分辨能力,将洪水时间序列在各时间段不同分量的能量值都显示出来了.EMD分解出的分量具有较为清晰的物理意义,具有自适应性;并且由于其对结果的表达手段多样,有利于对各个分量做进一步的精确分析.Hilbert-Huang变换存在的缺陷有:两端的数据会有所偏离,即所谓的“端点飞翼”现象,这是采用3次样条插值来获得信号的瞬时平均值,使得这种方法存在特殊的端点飞翼,即端点效应[12].
3 小结
洪水时间序列受天气系统的影响、降雨因素的作用,加上人类活动和水文下垫面的叠加,使得洪水时间序列存在多层次时间结构,并呈现非平稳性,直接表现为洪水时间序列的波峰和波谷交错在一起,波峰、波谷位置难以分辨.因此,仅对于洪水过程进行时间域上的分析不能完全显现出洪水时间序列的本质特性,需进一步探究洪水时间序列的频域特性,本研究 采用希尔伯特-黄变换的时-频分析方法处理洪水时间序列.研究表明,HHT变换对洪水时间序列进行分析时,基本上能将洪水时间序列在各时间段的不同分量的能量值显示出来.但由于Hilbert-Huang变换采用3次样条插值来获得信号的瞬时平均值,结果会出现“端点飞翼”现象.
[1] HUANG N E,ZHENG S,STEVEN R L. A new view of nonlinear water waves: The Hilbert spectrum[J]. Annu Rev Fliud Mech, 1999,31: 417-457.
[2] 刘卓夫,廖振鹏,桑恩方.基于希尔伯特黄变换的滤波器设计[J].信号处理,2005,21(S1):456-458.
[3] 于德介,程军圣,杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京:科学出版社,2006:1-44.
[4] LOH C H,WU T C,HUANG N E,et al. Application of emd + HHT method to identify near-fault ground motion characteristics and structural responses[J]. BSSA,Special Issue of Chi-Chi Earthquake,2001,91(5):1339-1357.
[5] HUANG W,SHEN Z,HUANG N E,et al. Nonlinear indicial response of complex nonstationary oscillations as pulmonary hypertension responding to step hypoxia[J]. Proc Natl Acad Sci USA,1999,96:1834-1839.
[6] 肖立波,任建亭.基于Hilbert-Huang变换的非线性振动系统的研究[J].计算机应用研究,2011,28(3):880-882.
[7] 孙志刚,翟玮星,李伟伦,等.基于EMD和相关向量机的短期负荷预测[J].电力系统及其自动化学报,2011,23(1):92-97.
[8] 玄兆燕,杨公训.经验模态分解法在大气时间序列与预测中的应用[J].自动化学报,2008,34(1):97-101.
[9] 万星,周建中,刘力,等.基于希尔伯特-黄变换与小波方法的径流序列分析[J].华中科技大学学报:自然科学版,2008,36(1):107-111.
[10] 冯志华,朱忠奎,刘刚,等.经验模态分解方法的小波消失现象[J].数据采集与处理,2006,21(4):478-481.
[11] 江四厚,陈小虎,王汉功,等. 基于Hilbert-Huang变换的振动信号特征提取[J].机床与液压,2008,36(11):199-201.
[12] 杜爱明,王彬,杨润海.Hilbert-Huang变换中的一种端点处理方法[J].地震研究,2007,30(1):54-58.
StudyonFrequencyDomainsofFloodbyUsingEmpiricalModeDecompositionandHHT
WANG Lina1*, LI Yan2, CHEN Xiaohong3,4
(1. School of Geography Science; South China Normal Univeristy; Guangzhou 510631; China; 2.Department of Tourism and Environment, Guangdong University of Business Studied, Guangzhou 510320, China; 3.Center for Water Resources and Environment; Sun Yat-sen University; Guangzhou 510275; China; 4.Key Laboratory of Guangdong Provincial Water and Water Security in South China)
According to the empirical mode decomposition and HHT, this paper analysis the flood process. The six floods processes have been study on the Wujiang River. The results showed that: the flood energy has concentrated in 0.1 Hz. And floods showed flood time series have more energy components characteristics. All components, which has decomposed by EMD method, have a clearer physical meaning. The signal instantaneous average, which can be obtain by 3-spline interpolation, brought endpoint winger phenomenon.
2011-04-23
国家重点基础研究发展计划(973)项目(2010CB428405);国家自然科学基金项目(50839005;41001019);广东省自然科学基金博士启动项目(S2011040005992);广东高校优秀青年创新人才培养计划(育苗工程)项目(LYM11049);教育部高等学校博士学科点专项科研基金新教师类资助课题(20114407120006)
*通讯作者,linawang2004@163.com
1000-5463(2012)03-0128-04
K903
A
10.6054/j.jscnun.2012.06.027
Keywords: empirical mode decomposition; HHT; flood; frequency domains
【责任编辑 成 文】
