直线超声电机非线性模型辨识
2012-11-14张建桃张铁民
张建桃, 张铁民, 梁 莉, 文 晟
(1.华南农业大学信息学院,广东广州 510642;2.华南农业大学工程学院,广东广州 510642)
直线超声电机非线性模型辨识
张建桃1, 张铁民2*, 梁 莉2, 文 晟2
(1.华南农业大学信息学院,广东广州 510642;2.华南农业大学工程学院,广东广州 510642)
首先分析了直线超声电机在不同驱动条件下的阶跃响应,提出将直线超声电机速度模型简化为带纯延迟的一阶惯性系统,驱动频率和相位差对电机动态参数的影响转化为所建模型时间常数、系统增益和延时间参数的变化. 然后用最小二乘法辨识出模型参数与驱动频率和相位差之间的函数关系,建立了直线超声电机的调频、调相控制非线性模型,为直线超声电机高精度控制提供了模型依据. 最后,通过比较直线超声电机阶跃响应的实测值与仿真值,验证了所建模型的有效性.
直线超声电机; 频率; 相位差; 非线性; 系统辨识
与传统直线电磁电机相比,直线超声电机(LUSM)具有结构相对简单、体积小、重量轻、响应速度快、断电自保持、可获得低速大推力、不产生磁场和不受外界磁场干扰等特点[1]. 但直线超声电机结构与工作原理特殊,工作中含有摩擦过程,功率传递和运动特性包含许多非线性和不确定性因素,至今尚未建立能精确描述直线超声电机特性的动态模型.近年来,许多建模理论与方法被用于直线超声电机的建模,如等效电路模型[2]、机理分析模型[3],然而等效电路模型无法描述电机的动态特性,机理分析模型太复杂、参数太多,难以用于超声电机控制器的设计[4-5]. 所以,目前直线超声电机的控制多是采用PI、模糊控制、神经网络控制[6]等不需数学模型的一种或多种控制策略的综合,如LIN Faa-Jeng将小波技术、神经网络、自适应和滑模等多种控制策略相结合[7],用于直线超声电机的位置控制. 多种控制策略的组合导致算法复杂,计算量大,使控制时的离散化时间(采样时间)加长,影响控制效果,限制了超声电机优点的充分发挥[8]. 文献[4]和文献[9]采用辨识的方法,建立了旋转超声电机的非线性模型,但针对直线超声电机的辨识建模未见报道,本文尝试采用辨识的方法建立适于控制的辨识模型.
1 电机阶跃响应测量与分析
为了辨识直线超声电机速度模型,需要测量电机在不同输入条件下的阶跃响应,本文以V型直线超声电机为研究对象,采用LABView的电机速度测量系统(图1)[10]. 将函数信号发生器(型号:1946A,日本N.F.公司)产生的两相频率和相位差都可调的正弦信号,输入到功率放大器(型号:HSA4014,日本N.F.公司)和变压器后,驱动直线超声电机. 非接触式位移传感器(型号:TLM0100001411201,德国Novotechnik公司)将采集的电机位移信号,通过数据采集卡(型号:NI USB-6251,美国NI公司)采集到PC机,再用LABView软件计算出电机速度.
被测电机驱动频率和相位差的调节范围为:频率20.3~22 kHz,相位差-90°~90°(其中相位差的负号只影响电机运动方向). 在这个范围内,固定两相驱动信号相位差和电压峰-峰值,驱动频率分别为20.3 kHz和20.6 kHz时,电机的阶跃响应如图2中曲线f1、f2所示. 当固定两相驱动信号的频率和电压峰-峰值,相位差分别为90°和60°时,电机的阶跃响应如图2中曲线p1、p2所示. 从图2可以看出,不同驱动条件下的阶跃响应与带纯延迟的一阶惯性环节相似,因此可以设直线超声电机的传递函数为:
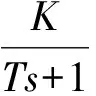
(1)
其中T是时间常数,K是增益,是纯延迟时间.
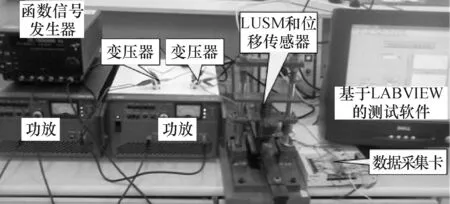
图1 阶跃响应测量系统实物照片
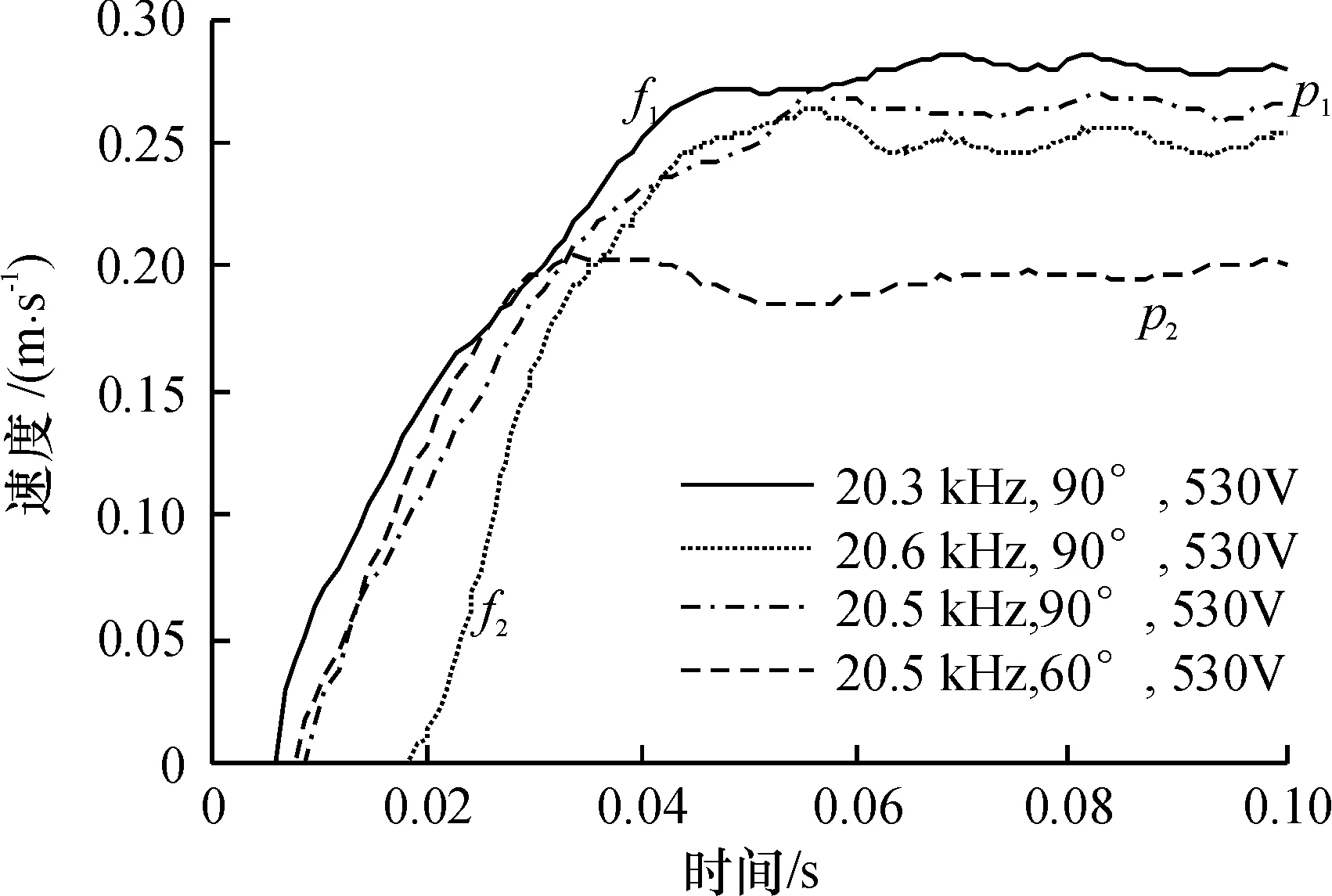
图2 不同驱动条件下的阶跃响应
图2的曲线f1和f2表明式(1)中的参数T、K和会随两相驱动信号频率f的变化而变化. 设参数T、K、与频率f的关系分别为T(f)、K(f)和(f),则直线超声电机的调频速度控制传递函数可以表示为:
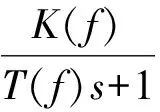
(2)
同理,从图2的曲线p1和p2看出,T、K和随相位差φ的变化而变化,可设电机的调相速度控制非线性模型表示为:
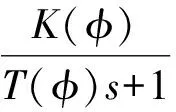
(3)
下面将采用辨识的方法辨识出式(2)和式(3)中的参数.
2 调频速度控制非线性模型
式(2)将驱动频率对直线超声电机动态参数的影响转化为系统参数K、T和与频率的关系,本节分析实验测量数据,辨识出T(f)、K(f)和(f).
为了获得调频时的增益参数K(f),在空载条件下,两相驱动信号的相位差分别设为90°、60°和30°,电压峰-峰值为530 V,在电机工作频率范围[20.3 kHz,22 kHz]内,选取不同的驱动频率,测得直线超声电机的速度,每个频率点重复测量3次,计算出电机的算术平均速度(图3),可看出,电机稳态速度与驱动频率呈线性关系,故可设
K(f)=a1f+a2,
(4)
其中,a1、a2是回归系数,采用Matlab软件中的曲线拟合函数polyfit()进行拟合,其结果见表1,其中R2为决定系数. 从决定系数的值可以得出,仿真值与实测值吻合较好.
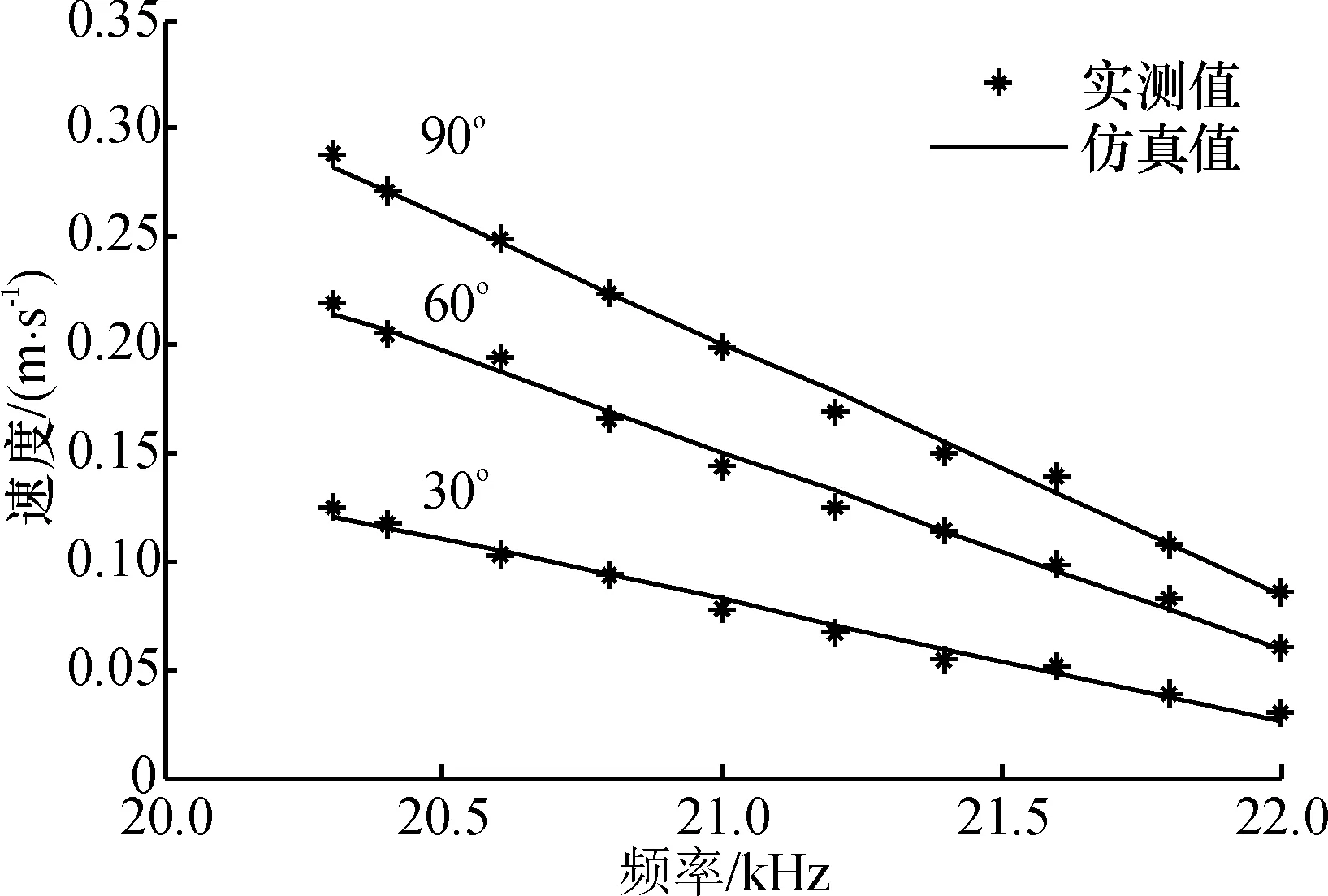
图3 LUSM速度-频率特性
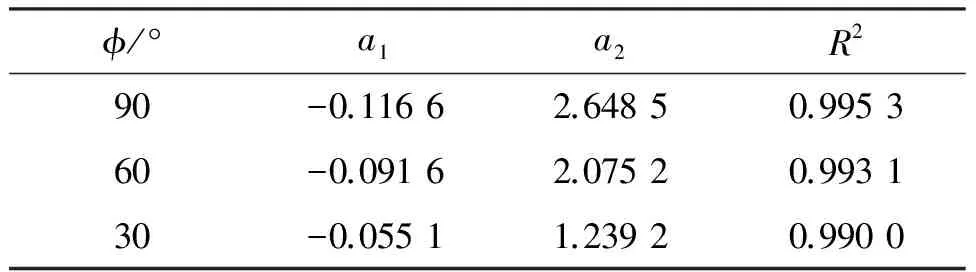
表1 式(4)辨识结果Table 1 Identified results of equation (4)
为了求得时间常数T(f)和纯延迟时间(f),在空载条件下,两相驱动信号的相位差固定为90°,电压峰-峰值为530 V,在电机工作频率范围[20.3 kHz,22 kHz]内,改变驱动频率,测量电机的阶跃响应,得到电机的过渡过程时间ts、纯延迟时间与驱动频率呈线性的关系(图4),而一阶系统过渡过程时间与时间常数的关系为ts=3T,因此,T(f)和(f)与驱动频率的关系分别可设为:
T(f)=b1f+b2,
(5)
(f)=c1f+c2.
(6)
式(5)、(6)中的参数用polyfit()函数拟合,回归结果为:b1=-0.005 1,b2=0.113 5,c1=0.031 1,c2=-0.622 6. 从图4可以看出,模型输出值与实测值吻合较好.
根据式(2)、式(4)~ (6)及其回归结果,V型直线超声电机的调频速度控制非线性模型可表示为:
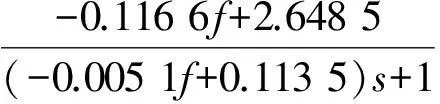
(7)
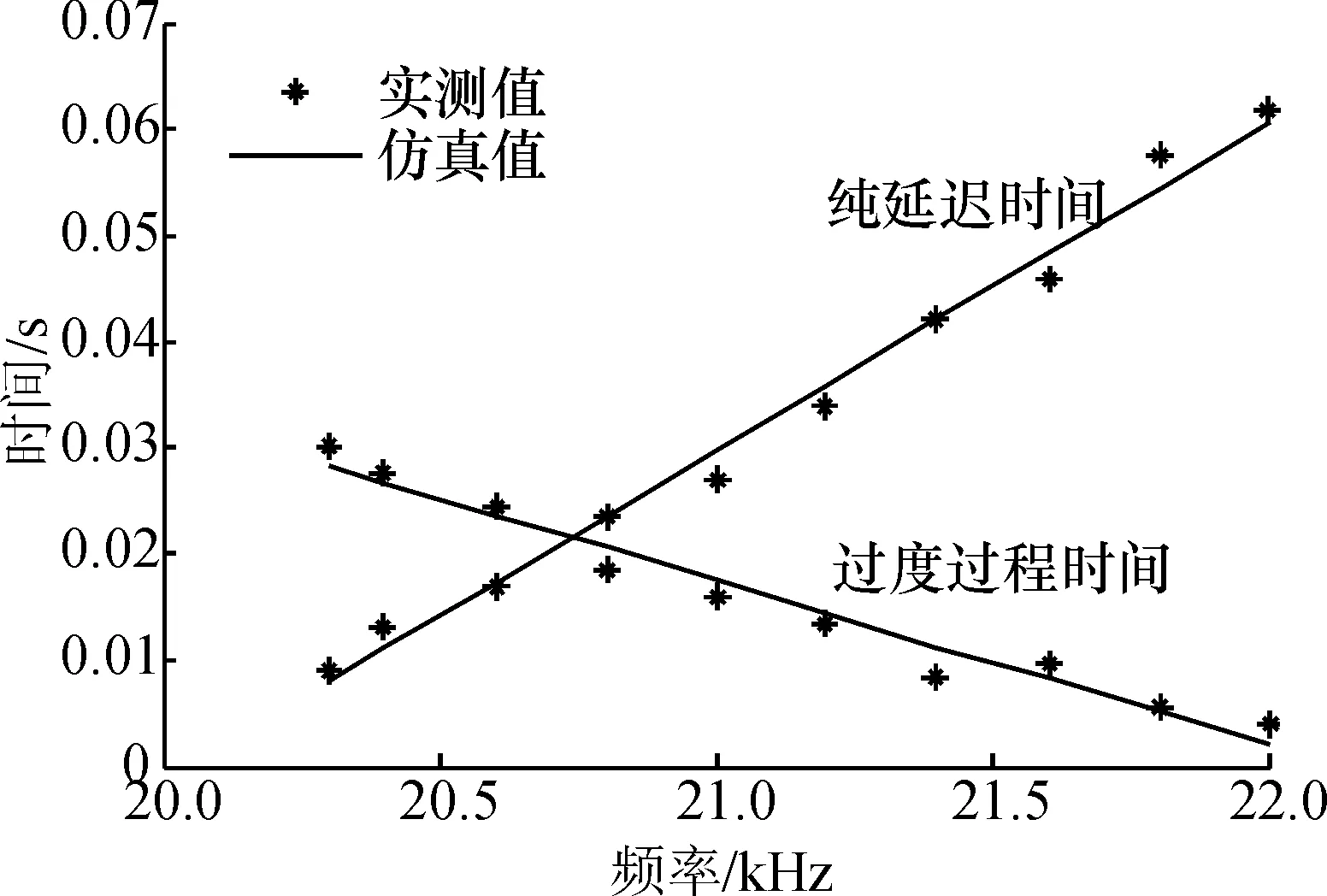
图4 T(f)和 (f)与驱动频率的关系图
3 调相速度控制非线性模型
式(3)将相位差对直线超声电机动态参数的影响转化为系统参数K、T和与频率的关系,本节将辨识出T(φ),K(φ)和(φ).
为了获得增益参数K(φ),在空载条件下,驱动频率分别固定为20.5、21.0、21.5 kHz,电压峰-峰值为530 V,两相驱动信号相位差在[-90°,90°]的范围内变化时,对V型直线超声电机的速度进行测量,结果如图5所示,电机稳态速度与相位差呈双曲正切函数关系,故可设
K(φ)=a1tanh(a2φ),
(8)
其中K(φ)是直线超声电机稳态速度,也就是式(3)中的增益,a1、a2是回归系数,采用Matlab软件中的参数估计函数nlinfit( )回归,结果如表2所示,决定系数的值接近1,说明模型输出值与实测值吻合较好.

图5 LUSM速度-相位差特性
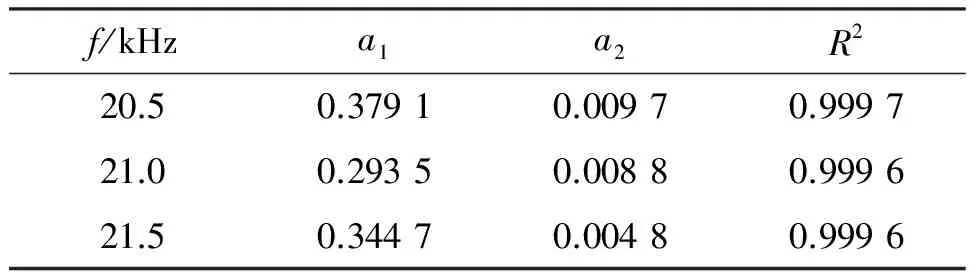
表2 式(8)辨识结果Table 2 Identified results of equation (8)
为了辨识时间常数T(φ)和纯延迟时间(φ),在空载条件下,驱动频率固定在20.3 kHz,电压峰-峰值为530 V,相位差在[10°,90°]的范围内变化时,对V型直线超声电机的阶跃响应进行测量,从图6可看出,过渡过程时间与相位差的关系曲线类似于指数函数,(φ)与相位差呈线性关系,故可设:
T(φ)=exp(b1φ+b2),
(9)
(φ)=c1φ+c2,
(10)
参数b1、b2、c1和c2采用最小二乘法进行回归,可得:b1=0.036 0,b2=-7.384 2;c1=-0.000 07,c2=0.009 3.
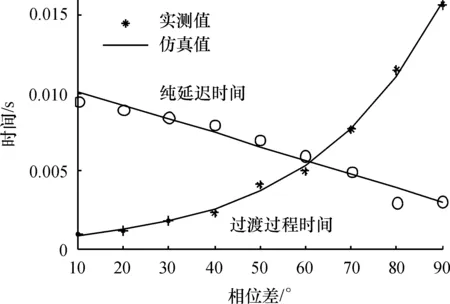
图6 T(φ)和 (φ)与相位差的关系图
联合式(3)、(8)~(10),V型直线超声电机的调相速度控制非线性模型可以表示为:
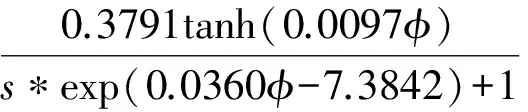
e(-0.00007φ+0.0093)s.
(11)
4 实验验证
为了验证所提出的V型直线超声电机调频、调相速度控制模型,对电机阶跃响应的实测值和模型输出值进行了比较. 图7(a)、(b)是调频速度模型式(7)的仿真曲线与实测值的对比. 图7(c)、(d)为调相速度控制模型式(11)的仿真曲线与实测值的对比. 比较图7中模型输出曲线(仿真值)与实测曲线,可知仿真值接近实测值,说明所建立的调频和调相速度控制模型能够较好地反映V型直线超声电机的动态特性.
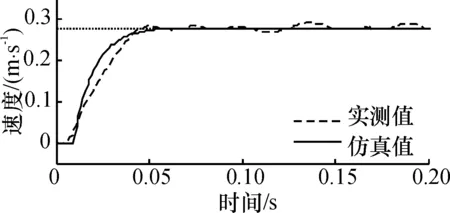
(a)f=20.3 kHz, φ=90°, u=530 V
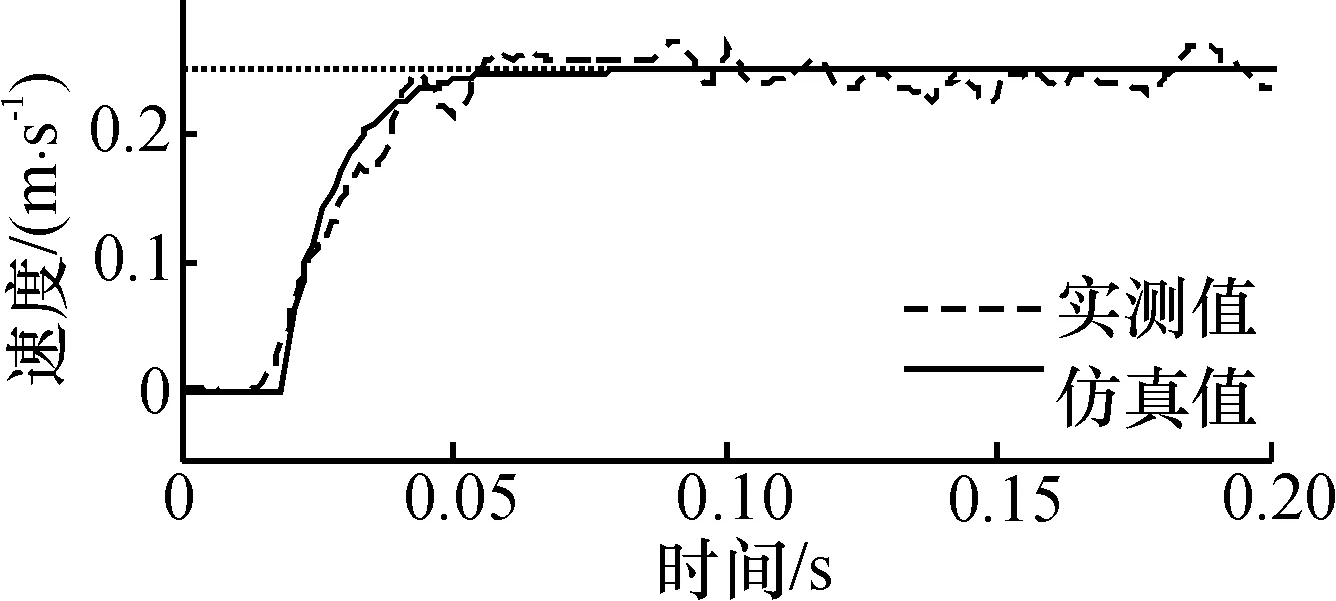
(b)f=20.6 kHz, φ=90°, u=530 V
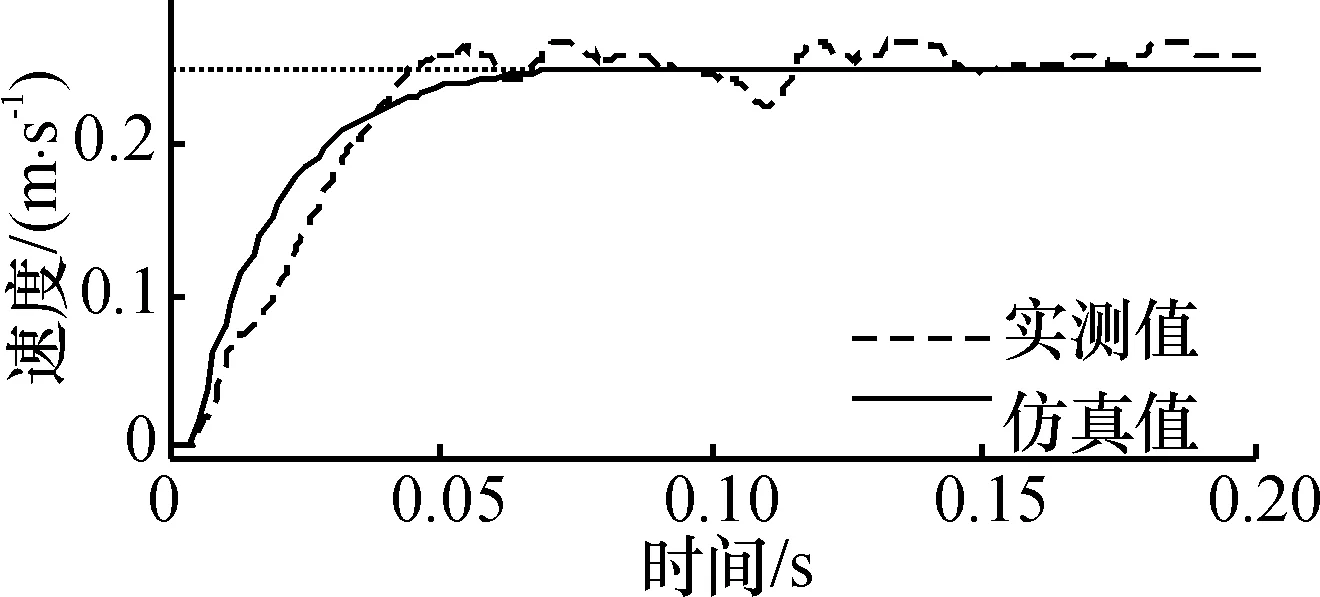
(c)φ= 90°, f=20.5 kHz, u=530 V
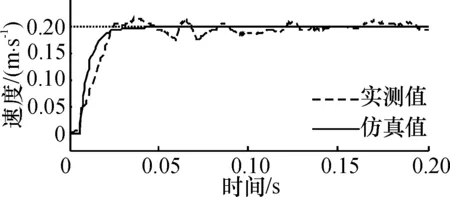
(d)φ= 60°, f=20.5 kHz, u=530 V
但图7中实际测量的阶跃响应曲线存在轻微的震荡,与仿真值存在一定误差,这是由本文将直线超声电机简化为一阶系统造成的,要得到更精确的模型,应将直线超声电机看作一个二阶或高阶系统.
5 结论
由于直线超声电机包含压电陶瓷的振动、摩擦等非线性因素,理论建模非常困难,本文避开这一难点,在对电机阶跃响应测量数据分析的基础上,提出将直线超声电机调频、调相速度控制模型简化为带纯延迟的一阶惯性环节,通过辨识建立了电机的调频和调相两个非线性模型. 调频速度控制模型的增益K、时间常数T和系统纯延迟时间与驱动频率都呈线性关系. 调相速度控制模型增益K与两相驱动信号的相位差φ呈双曲正切关系,时间常数T与φ呈指数关系,系统纯延迟时间与φ呈线性关系. 仿真和实验结果证实了模型的有效性. 所建的调频、调相模型具有参数少,适合用于直线超声电机的控制器的设计,为直线超声电机高精度控制提供了模型依据.
[1] 周铁英, 鹿存跃, 陈宇.毫米压电微电机的发展与应用[J].微特电机,2005(12):41-44.
[2] MANABU Aoyagi, YOSHIRO Tomikawa, TAKEHIRO Takano. Simplified equivalent circuit of an ultrasonic motor and its applications[J]. Ultrasonics,1996,34:275-278.
[3] ZHOU H, TAN K K,LEE T H. Micro-positioning of linear piezoelectric motors based on a learning nonlinear PID controller[C]∥Proceedings of the 39th IEEE Conference on Decision and Control. Sydney,Australia,2000:913-918.
[4] ZHANG Xinliang, TAN Yonghong. Modelling of ultrasonic motor with dead-zone based on Hammerstein model structure[J]. Journal of Zhejiang University: Science A,2008,9(1):58-64.
[5] 张新良,谭永红.行波型超声电机基于输入电压变化的参数模型辨识[J].系统仿真学报,2008,20(13):3492-3499.
[6] 孙志峻, 帅双辉, 金家楣,等. 基于径向基神经网络的直线超声电机位置控制[J].振动、测试与诊断,2010,30(6):650-653.
[7] LIN Faajeng, WAI Rongjong, CHEN Muping. Wavelet neural network control for linear ultrasonic motor drive via adaptive sliding-mode technique[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control,2003,50(6):686-699.
[8] 王心坚,金龙,尧波,等.行波超声波电机非参数辨识模型[J].中国电机工程学报,2008,28(18):83-89.
[9] 张建桃,张铁民, 梁莉. 超声电机非线性建模与广义预测控制[J]. 电机与控制学报, 2011,15(6):50-56.
[10] 武威,张铁民. 基于虚拟仪器的超声电机测试系统[J]. 仪器仪表学报,2009,30(6):493-496.
NonlinearModelIdentificationofLinearUltrasonicMotor
ZHANG Jiantao1, ZHANG Tiemin2*, LIANG Li2, WEN Sheng2
(1.College of Information, South China Agricultural University, Guangzhou 510642, China;2. College of Engineering, South China Agricultural University, Guangzhou 510642, China)
Since the speed characteristic of linear ultrasonic motor (LUSM) has strongly nonlinear property, it is difficult to derive an accurately mathematic model in theory. This problem is tried to be solved and a modeling method by identification is proposed. Firstly, the step responses of LUSM in different driving conditions were analyzed. It was proposed here that the model of LUSM can be simplified as one-order inertial pure lagging systems. The idea is to transform the effect of the driving frequency and phase difference of two-phase driving voltages into the changes of the parameters in the proposed model, such as time constants, gains and delays. Secondly, these parameters were obtained by least-squares regression, and dynamic nonlinear models of LUSM for frequency-speed control and phase-difference-speed control were proposed, which provide model basis for high accuracy control of LUSM. Finally, the validity of the proposed method was confirmed by experimental results.
2011-10-09
国家自然科学基金项目(51177053)
*通讯作者,tm-zhang@163.com
1000-5463(2012)03-0064-04
TP391.9
A
10.6054/j.jscnun.2012.06.014
Keywords: linear ultrasonic motor; frequency; phase difference; nonlinearity; system identification
【责任编辑 庄晓琼】
