一类渗流模型弱解的唯一性
2012-11-14宋瑞凤周裕中
方 平, 宋瑞凤, 周裕中, 张 昕
(1.华南农业大学理学院应用数学系,广东广州 510642;2. 华南农业大学农学院,广东广州 510642)
一类渗流模型弱解的唯一性
方 平1*, 宋瑞凤2, 周裕中1, 张 昕1
(1.华南农业大学理学院应用数学系,广东广州 510642;2. 华南农业大学农学院,广东广州 510642)
对三维渗流方程θ(ψ(x,y,z,t))t=div[k(ψ(x,y,z,t))ψ(x,y,z,t)]-(k(ψ(x,y,z,t)))z作变换化为(A(u))t=Δu-(k(u))z,通过构造一个特殊的检验函数,用反证法证明了三维渗流数学模型(I)弱解的唯一性.
渗流模型; 弱解; 唯一性; 反证法
渗流问题自上世纪50年代提出以来,得到了广泛而深入的研究,取得了许多进展,尤其是一维渗流问题得到了很好的解决[1-3].高维的情况,当k为常数时,相应的柯西问题的弱解的存在唯一性及其弱解的一些性质也得到了解决[4].本文将讨论k不为常数时的情况,即下述三维渗流方程:
θ(ψ(x,y,z,t))t=div[k(ψ(x,y,z,t))ψ(x,y,z,t)]-
(k(ψ(x,y,z,t)))z.
(1)
对方程(1)作类似文献[5]中的变换后可变为:
(A(u))t=Δu-(k(u))z,
(2)
其中θ、ψ、k、A的意义见文献[5],u=u(x,y,z,t),Δu=uxx+uyy+uzz.

(Ⅰ)
K1:k(s)在上Lipschitz连续;
K2:当s≤0时,k(s)=0;



C1:c(s)在上Lipschitz连续;


C4:c(s)在(-∞,σ0)上有连续的二阶导数.
u01:u0(x,y,z)在Q上连续有界;
u02:当x2+y2+z2≥a2(a为某一大于零的常数)时,u0(x,y,z)≡0;
当x2+y2+z2≤a2时,0≤u0(x,y,z)≤M0(M0>us为常数).
另外,k(s)与c(s)还满足:

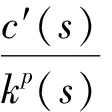




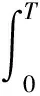
问题(I)的弱解的存在性及相应的比较原则已经得到证明[5],下面讨论问题(I)的弱解的唯一性.
为了后面定理证明的需要,先给出如下引理.
引理1 对于一个固定的常数E0>0,一定存在一个常数F0>0,使得:
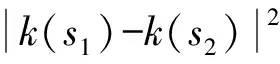

由条件KC1,本引理的证明类似文献[6]的引理1,此处从略.
下面给出本文的定理及其证明.
定理1 (唯一性定理)问题(I)至多只有一个弱解.
证明假设u1,u2是问题(I)的2个不同的弱解,那么存在一个常数
t0=sup{s|u1=u2a.e于Qs},
其中0 由于u1,u2均为问题(I)的2个弱解,则u1,u2均满足: 上述两式相减则有 (3) η(x,y,z,t)= (Ⅰ)0≤ak(x,y,z)≤1; 显然这样的ak是存在的.则可取 φ(x,y,z,s)=ak(x,y,z)η(x,y,z,t). 作为一个检验函数,将φ值代入式(3),有: (4) 因为ηt=-(u1-u2),(ηt)=-(u1-u2),[(η)2=2η(η)t=-2η·(u1-u2),即η·(u1-u2)=-[(η)2,从而 其中Qt1=Q×(0,t1],于是式(4)可变为: (k+1)2},Bkt1=Bk×(0,t1), 那么 从而 (5) 其中ε是大于零的待定常数,F1是大于零的常数.现取ε=(2F0)-1,由引理1可得: (6) 另外 (7) 由式(5)~(7)可得 (8) (9) 令 (10) 则有 η(x,y,z,t)=ζ(x,y,z,t1)-ζ(x,y,z,t) (11) ηz(x,y,z,t)=ζz(x,y,z,t1)-ζz(x,y,z,t) (12) η(x,y,z,0)=ζ(x,y,z,t1). 由A(s)的单调性知:(u1-u2)(A(u1)-A(u2))≥0,从而由式(9)~(12)可得: 由文献[7]的Gronwall引理可得: [1] OLEINIK O A,KALASNIKOV A S,CZOU Yui-lin.The cauchy problem and boundary problem for equations of the type of non-stationary filteration [J].Izv Akad Nauk Sssr Ser,1958,22:667-704. [2] XIAO Shutie,HUANG Zhida,ZHOU Chuanzhong.The infiltration problem with constant rate in partially saturated porous media[J].Acta Math Appl Sinica,1984,1(2):108-126. [3] XIAO Shutie,HUANG Zhida. One dimensional filtration problem in partially saturated porous media[J].Acta Math Appl Sinica,1996,12(4):418-426. [4] ZHANG Daowen. The propagating speed problem of solutions to the filtration equation in N-dimensional porous medium[D].Beijing:Peking University,1986. [5] 方平,周裕中,张昕,等. 一类渗流模型弱解的存在性[J].江西师范大学学报,2009,33(4): 467-470. [6] GILDING B H.A nonlinear degenerat parablic equations[J].Anali Della Scuo Nor Sup Di Pisa,1977,4:393-432. [7] LADYZHENSKAJA O A,SOLONNIKOV V A, URAL’CEVA N N. Linear and quasilinear equations of parabolic type[M]. Providence:American Mathematical Society,1968. TheUniquenessoftheWeakSolutionoftheInfiltrationModel FANG Ping1*, SONG Ruifeng2, ZHOU Yuzhong1, ZHANG Xin1 The three-dimensional infiltration equationθ(ψ(x,y,z,t))t=div[k(ψ(x,y,z,t))ψ(x,y,z,t)]-(k(ψ(x,y,z,t)))zwas transformed into (A(u))t=Δu-(k(u))z. By constructing a special test function, the uniqueness of the weak solution of this model was proved with reduction to absurdity. 2012-03-16 国家自然科学基金项目(11071083);广东高校优秀青年创新人才培养计划项目(粤财教[2008]350号) *通讯作者,squareflat@163.com 1000-5463(2012)03-0028-04 O175.2 A 10.6054/j.jscnun.2012.06.006 Keywords: infiltration model; weak solution; uniqueness; reduction to absurdity 【责任编辑 庄晓琼】

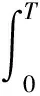


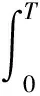





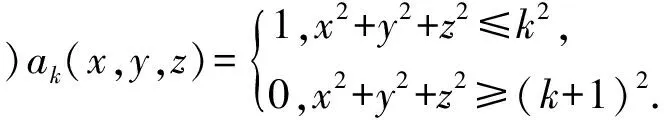




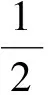
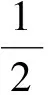
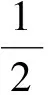
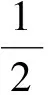

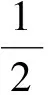






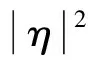
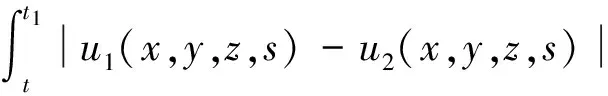
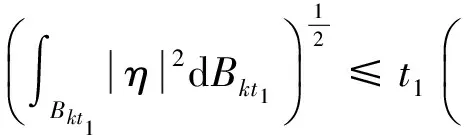







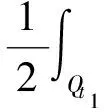


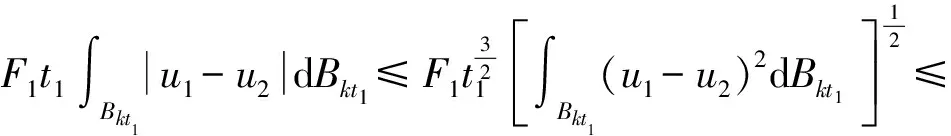

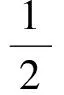




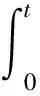
(0≤t≤t1),
(0≤t≤t1),
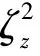





(1. Department of Mathematic, College of Science, South China Agricultural University, Guangzhou 510642, China;2. College of Agriculture, South China Agricultural University, Guangzhou 510642, China)
