约束优化问题中LP最小值序列的性质和判定
2012-11-14罗桂美
罗桂美
(广东金融学院应用数学系,广东广州 510521)
约束优化问题中LP最小值序列的性质和判定
罗桂美
(广东金融学院应用数学系,广东广州 510521)
从凸函数的次微分出发, 采用非光滑分析的方法,考察约束优化问题中当约束集为非空闭凸锥时,LP最小值序列的性质及判定方法,并进一步考察Banach空间中当约束为不等式时的特殊情形.
锥凸最优化; 不等式约束; LP最小值序列; 性质; 判定
1 引言及预备知识
在处理约束优化问题
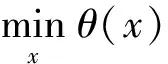
(1)
的最优解时,很多情况下都将其转化成给定一个误差范围, 在该范围内寻求近似最优解,从而得到一个近似最优解序列{xk},再判断该序列是否是最小值序列,其中θ为从N到上的函数,K是N中的非空闭凸集. 对此类问题的研究, 可参考文献[1]-[4]及相应的文献, 其中文献[1]要求θ:N→为连续可微函数,且序列{xk}⊆K,文献[2]主要考察θ为非光滑函数但无约束时的情形,文献[3]研究了当θ为凸函数且约束集为闭凸集时,稳定序列与最小值序列之间的关系同时给出了迭代算法,并证明了当目标函数满足某种正则性及一致连续的假设时,由该算法产生的序列为最小值序列, 文献[4]研究的问题是:在局部李普希兹条件下, 给定D-gap函数的一个稳定序,寻求该序列成为最小值序列的条件; 反之, 给定D-gap函数的一个最小值序列,寻求该序列成为稳定序列的条件.上述研究大多数是考虑落在约束集K内的序列,而实际上落在K内的序列{xk}通常并不具有我们想要的性质,因此有必要研究约束集K边界附近且具有良好性质的那些点列,如LP最小值序列, 可参见文献[5]-[8]及相应的文献.然而,当K为非空闭凸集时,判定一个序列{xk}是否为LP最小值序列的条件非常严格. 基于此,本文在θ为正常凸函数、K为非空闭凸锥情况下,采用非光滑分析的方法,侧重考察LP最小值序列的良好性质以及序列成为LP最小值序列的条件.并将此结论推广到Banach空间约束集合K为不等式约束集合的情形.
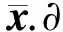
定义1 称序列{xk}⊂N是θ在K上的一个LP最小值序列, 若
i){xk}是渐近可行的,即dist(xk,K)→0;
ii){xk}是渐近最优的, 即θ(xk)→θinf.
若i)改为可行的, 即{xk}⊂K,则称{xk}是θ在K上的一个最小值序列.
定义2 称序列{xk}⊂N是AC-稳定的(AC代表Auslender和Crouzeix), 若i){xk}是渐近可行的;ii)存在ak∂φs.t.ak→0,其中φ:=θ+IK,IK为K的指示函数.易知
其中NK(x)表示K在点x处的法锥.
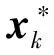

∂θ(w)⊆∂θ(xk)+εB(0,1).
相应地, 可得到下半连续的定义. 特别地,由文献[9]中定义3.3.1后的注3.3.1知, 当Y=且F=θ:X→是实值函数时,定义4即为θ在{xk}附近一致连续,本文中θ在{xk}附近一致连续就采用此定义, 即
定义5 称函数θ:N→M在{xk}附近是一致连续的,如果对∀ε>0,存在δ>0,使得对所有的k和yN,都有‖y-xk‖≤δ⟹‖θ(y)-θ(xk)‖≤ε.有了上述定义, 容易证明下面引理成立.
引理1 设θ的次微分映射在{xk}附近是一致上半连续且关于序列{xk}有界,则θ在{xk}附近一致连续.
引理1的证明可参见文献[6]的引理1.
引理2 设θinf>-∞.设{xk}是θ在K上的LP最小值序列.若{xk}满足条件(i){xk}可行,或条件(ii)θ在{xk}附近一致连续. 则存在{yk}⊂K,使得
(1)yk-xk→0;
(2){yk}是θ在K上的一个最小值序列且是AC-稳定的;

引理2的证明可参见文献[7]的定理1及文献[2]的定理3.2.
引理3[10]若f1,f2都是N上的正常凸函数且满足ri(domf1)∩ri(domf2)≠.令f(x)=f1(x)+f2(x),则∂f(x)=∂f1(x)+∂f2(x),∀x.
2 主要结论
下面定理在问题(1)中的约束K为一非空闭凸锥时, 用非光滑分析的方法将其结果推广到了下半连续正常凸,{xk}渐近可行的最优化问题中.
定理1 设θinf>-∞,K是N上的非空闭凸锥.
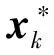
(2)
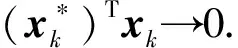
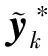

(3)
因K是锥,分别取y=2yk及y=yk/2代入式(3), 即得(wk)Tyk=0, ∀k.故有


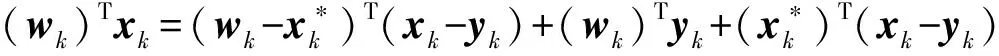
若{xk}有界,则
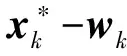
ii)用反证法. 假设{xk}不是θ在K上的一个LP最小值序列,则存在0>θinf, 存在{xki}⊆{xk}满足θ(xki)>0,∀i及0.又L(0)是N中的非空闭凸子集, 所以对每一ki,存在yiL(0)⊆K,使得‖xki-yi‖=dist(xki,L(0)).从而θ(yi)≤0.
由θ的次微分定义知,
从而
θ(xki)-0≤θ(xki)-θ(yi)≤()T(xki-yi)=

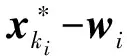

两边同除以θ(xki)-0,得:
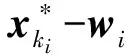
对两边取极限,左边为1,右边趋向于零, 矛盾.
□
特别地,若问题(1)中的约束集合K为不等式约束集时, 问题(1)变为:
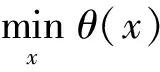
(4)
文献[9]在θ,Gi(i=1,2,…,M)均为Banach空间上的正常凸函数且每个Gi存在Slater点(可参见文献[9]的定义3.4.2)情况下考虑了最优解与KKT条件之间的关系; 文献[1]在θ,Gi(i=1,2,…,M)均为连续可微且{xk}可行情况下, 把该性质由单个向量x推广到最小值序列中. 下面主要讨论问题(4)中, 当θ,Gi(i=1,2,…,M):N→∪{+∞}为正常凸函数, 且每个Gi(i=1,2,…,M)存在Slater点时,LP最小值序列与渐进KKT条件之间的关系,得到的结论也可看成当约束为不等式时LP最小值序列的性质和判定方法.为此,进一步记问题(4)的可行域为X且假设X≠.
定理2 设θinf>-∞,{xk}是X中的任意一个点列.每个Gi(i=1,2,…,M)是N上的正常凸函数且存在Slater点.
i)若{xk}是θ在X上的一个LP最小值序列,θ的次微分在{xk}附近一致上半连续且关于{xk}有界,那么存在{μk}⊂使得
(5)
(6)
证明i)由引理1知,θ在{xk}附近一致连续. 由引理2知, 存在{yk}⊂X使得yk=PX(yk-wk).所以yk是下面规划问题的最优解:

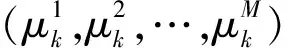
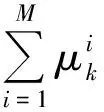
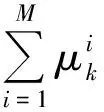
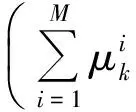
-‖wk‖·‖yk-xk‖→0.
下证定理后半部分.
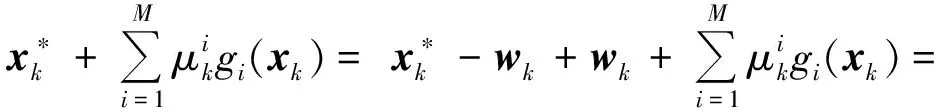
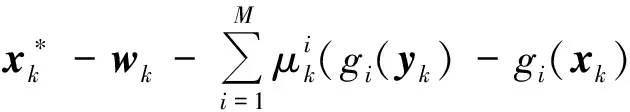
ii)仿照定理1,ii)即可得证.
□
3 结束语
本文从凸函数的次微分定义出发,采用非光滑分析的方法,研究了锥凸最优化问题中的LP最小值序列的性质及判断方法,并考察了Banach空间中约束为不等式时,LP最小值序列与渐进KKT条件的关系,进一步可看成是约束为不等式时LP最小值序列的性质与判定.这些结论是原有文献中相应结论的推广.
[1] CHOU C C, NG K F, PANG J S. Minimizing and stationary sequences of constrained optimization problems[J]. SIAM Journal of Control and Optimization, 1998(36): 1908-1936.
[2] HUANG L R, NG K F, PENOT J P. On minimizing and critical sequences in nonsmooth optimization[J]. SIAM Journal on Optimization, 2000(10): 999-1019.
[3] HE Y R. Minimizing and stationary sequences of convex constrained minimization problems[J]. Journal of Optimization Theory and Applications, 2001(1): 137-153.
[4] NG K F, TAN L L. D-gap function for nonsmooth variational inequality problems[J]. Journal of Optimization Theory and Applications, 2007(133): 77-97.
[5] 李传乐. 约束最优化问题的稳定序列[J]. 华南师范大学学报:自然科学版, 2001(2): 65-40.
[6] 李传乐,黄力人. 非光滑约束最优化的稳定序列和最小值序列[J]. 湛江师范学院学报, 2003,24(3): 4-8.
[7] 罗桂美. 约束最优化问题中的LP最小值序列[J]. 绍兴文理学院学报, 2004,24(10): 13-15.
[8] 罗桂美. 约束优化中的渐近稳定序列与LP最小值序列[J]. 福州大学学报:自然科学版, 2011,39(3): 339-344.
[9] 胡毓达,孟志青. 凸分析与非光滑分析[M]. 上海:上海科学技术出版社, 2000.
[10] 刘光中. 凸分析与极值问题[M]. 北京: 高等教育出版社, 1991.
PropertiesandJudgementofLPMinimizingSequenceonConstrainedOptimizationProblems
LUO Guimei
(Department of Applied Mathematics, Guangdong University of Finance, Guangzhou 510521, China)
Using non-smooth and subdifferential analysis, some properties and judgement of LP minimizing sequence are investigated when the constraint subset inNspace is a non-empty closed convex cone. Furthermore, a special case of inequality constraints in Banach space is considered.
2011-12-06
国家自然科学基金项目(11071087);广东省自然科学基金项目(S2011040000805)
*通讯作者,gmluo@sina.cn
1000-5463(2012)03-0025-03
O224
A
10.6054/j.jscnun.2012.06.005
Keywords: convex cone optimization; inequality constraint; LP minimizing sequence; property; judgement
【责任编辑 庄晓琼】
