小波去噪质量评价方法的对比研究*

陶 珂 朱建军

(中南大学测绘与国土信息工程系，长沙 410083)

小波去噪质量评价方法的对比研究*

陶 珂 朱建军

(中南大学测绘与国土信息工程系，长沙 410083)

针对小波去噪的特点，研究了现有小波去噪质量评价方法的实际应用效果。通过实验分析与比较，得到了现有5种小波去噪质量评价方法的实际评估能力。

小波变换;小波去噪;质量评价;测量数据;数据处理

1 引言

自20世纪90年代以来，小波分析以其良好的时频局部化和多分辨率分析的能力而在测量数据处理领域得到广泛的应用和越来越多的重视［1-6］。借助小波分解与重构技术，可以有效地滤除观测信号中的噪声，提高数据处理结果的可靠性。但是需要指出的是，虽然小波去噪技术已经在大地测量数据处理领域得到广泛应用，但应用效果并非极佳。其中一个重要的原因在于:实际应用中很难掌握实际信号的真实特征，故难以对小波去噪的质量进行准确评价，从而导致最佳分析结果的选取非常困难。

现有的小波去噪质量评价方法主要源于经典统计学，而小波去噪从根本上讲是基于非统计原理，其特点在于:小波分析技术不考虑系统的概率分布，允许系统的概率分布是未知的或非典型的［7］。因此，基于经典统计学的质量评价方法在小波去噪中的应用效果需要进行专门的研究并得到充分的重视。为此，本文将系统研究现有小波质量评价方法的实际应用效果，并总结各种评价方法的评价能力与特点。

2 小波去噪的基本原理

小波变换的基本思想是用2个或2个以上的函数(小波基)去逼近原函数［8］。设信号x(t)是平方可积函数，则x(t)的小波变换为该信号与小波函数ψ(α，τ)(t)的内积，为:

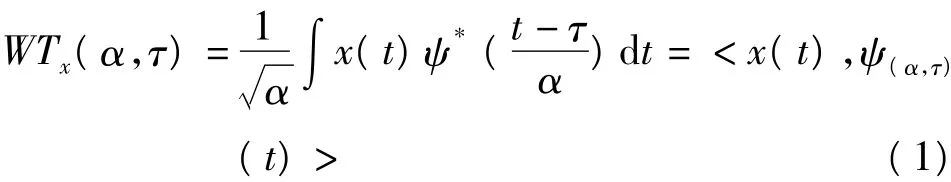
式中α和τ分别为伸缩和平移因子，ψ*(t)是ψ(t)的共轭。

小波变换实际上是对函数的分解，小波变换具有带通的功能，即可以利用小波变换将原信号分解成不同频率的信号，每个频率带互不重叠，所分解的频率区间包含了原函数的所有频段。由于信号中的有用部分与噪声具有不同的时频特性，如变形监测数据中，变形信号通常表现为低频信号或是一些比较平稳的信号，而噪声信号则主要集中在小波分解的高频层。因此，通过选取合理的阈值可以有效去掉噪声信号，进而小波去噪主要包括以下3个基本步骤［2-6］:

1)选择小波基以及分解层次，计算各层小波分解系数;

2)针对每一分解层次选择一个阈值，对高频系数进行处理，去除集中在高频部分的噪声成分;

3)针对每个分解层次，对低频系数和阈值量化处理后的高频系数进行小波重构，获得去噪后的信号。

3 小波去噪质量评价方法

现有小波去噪质量评价方法主要有5种，现分别对其进行简要介绍。

3.1 均方根误差［9］

均方根误差指分解与重构信号与原始信号的均方误差，记为RMSE，

均方误差体现了原始信号和去噪之后的信号间的差异，实际使用时，均方误差越小表示去噪效果越好。

3.2 信噪比和信噪比增益［10］

信噪比指原始信号能量与噪声能量的比值，记为SNR，

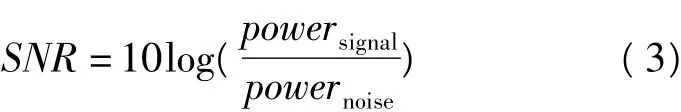
信噪比增益指小波去噪后的信噪比与去噪前的原始信噪比的比值，记为GSNR，

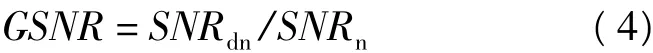
式中SNRdn表示去噪后的信噪比，SNRn表示原始信号的信噪比。

一般认为，信噪比越高、信噪比增益越大，则滤波效果越好。

3.3 平滑度指标［11］

平滑度指标指去噪后信号的差分数的方差根与原始信号的差分数的方差根之比，记为r，

信号越光滑，平滑度指标的数值就越小，则去噪效果越好。

3.4 互相关系数［12］

互相关系数指小波去噪后的信号与理论参考信号的相似度，记为R，

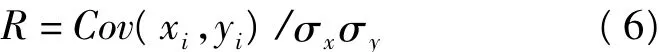
式中Cov(xi，yi)为xi和yi的协方差，σx、σy分别为xi、yi的标准差。

R越接近1，去噪效果越好。

3.5 总体评价法［13］

总体评价法综合考虑了均方根差变化量、信噪比、平滑度以及互相关系数等度量指标，将其归化到［0，1］区间相加获得，记为H，则:

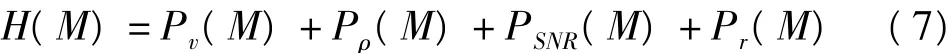
式中Pv(M)表示均方误差变化量的归一化值，Pρ(M)、PSNR(M)、Pr(M)分别表示互相关系数、信噪比、平滑度的归一化值。实际使用时，总体评价指标值越大，则认为小波去噪效果越好。

4 实验设计与分析

4.1 实验设计

小波分析质量评价方法在实际上主要有两方面用途［8，11-13］:1)选择小波去噪的最佳分解与重构层次;2)评价不同去噪结果的可靠性。为此，本文实验设计的目的也主要为了检验小波去噪质量评价方法在这两方面的应用效果:1)针对一个小波去噪过程，是否可以指导选择最佳的分解层次;2)针对不同的小波去噪方法，是否可以指导选择最佳的去噪结果。

设计实验数据时首先需要考虑两方面因素:1)为了能够准确地获得小波去噪质量的实际评价效果，需要选取真值已知的数据进行分析;2)为了全面反映小波去噪质量评价方法的应用效果，需要充分顾及实际去噪数据的固有特性。通过分析已有的研究成果［2-5，14］，可以发现去噪数据主要存在3方面的差异:1)平滑度差异，即真实数据中是否存在较多的突变;2)真实数据可能存在平稳和非平稳两种情况;3)不同信噪比(高或低)的去噪信号。针对去噪信号的差异，本文针对性地选择两组数据: Blocks标准信号(图1(a)，N=1 024)和一组模拟的变形监测数据S(图1(d)，N=1 024)，其中模拟数据采用3个不同频率的正弦信号以及一个低频趋势信号叠加产生一个模拟的变形监测数据:

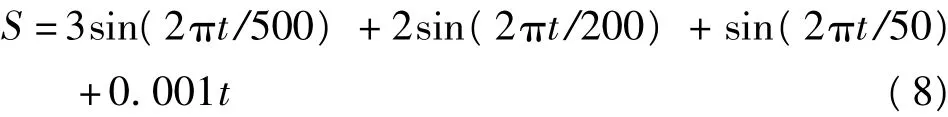
Blocks信号为各类信号处理实验的标准信号，因其具有代表性及普适性，且真知已知，所以本文将其选为实验数据;模拟数据是根据变形监测数据的实际情况进行模拟的，选用不同频率的正弦信号模拟实际数据中不同频率的成分，低频趋势部分用来模拟实际形变的走势。

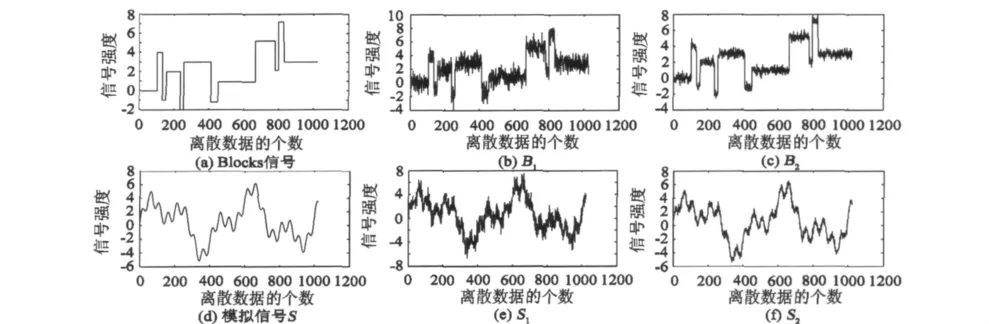
图1 实验数据Fig.1 Experimental data

分析图1中6组实验数据可以发现:1)Blocks标准信号和模拟信号S分别表示了平滑度不同的真实信号，其中Blocks标准信号存在角度的突变，而模拟信号S变化较为平缓;2)由于实际信号非平稳的情况较多，故Blocks标准信号和模拟信号S均包含了一定的趋势成分，因此均是非平稳的;3)针对真实Blocks标准信号和模拟信号S分别加入不同信噪比(高或低)的噪声，生成4组去噪信号。其中B1(图1(b))和S1(图1(e))为加入信噪比为2的白噪声的去噪信号，B2(图1(c))和S2(图1(d))为加入信噪比为10的白噪声的去噪信号。可见，本文设计的4组去噪信号可以充分顾及实际去噪信号的固有特点且真值已知，对去噪结果具有准确的先验知识。由于标准信号已知，即已知未加噪声的纯净信号，所以可求得重构信号与原始纯净信号的均方误差值(区别于评价标准中的RMSE)，当该均方误差最小时，视为最佳去噪结果。

实验分析时，为检验小波去噪质量评价方法的不同用途，分别采取如下实验方法:1)选取一种小波基，分别进行8个层次的分解与重构，以检验去噪评价方法对于不完全去噪、完全去噪及过度去噪情况下的识别效果;2)选取3种常用的小波基haar、db8和sym6，用来获得不同的小波去噪方法。

基于以上实验设计原则与方法，下面将通过具体实验分析现有5类(6种)小波去噪质量评价方法的实际评价效果与规律。

4.2 Blocks标准信号实验分析

以包含较多噪声的信号B1为例，说明实验的具体实施过程。通过计算重构信号与原始纯净信号的均方误差后发现，采用haar小波基在第5层次上的去噪效果最好。图2展示了各类评价方法对haar小波基8个层次分解重构结果的评价变化曲线。分析可以发现:1)根据评价标准的定义和要求，没有一种指标可以准确识别正确的分解层次;2)RMSE、SNR、GSNR和R基本上是单调递增或递减的，并没有极值出现;3)H指标虽然对应有一个最大值，即当分解层数为7时，但其结果确是错误的。

表2展示了分解层数为5时，6种评价方法针对haar、db8和sym6 3种小波基对信号B1去噪结果的评价。可见:1)RMSE、SNR以及GSNR 3种评价方法得到了正确结论;2)r、R和H方法则无法得出正确结论。

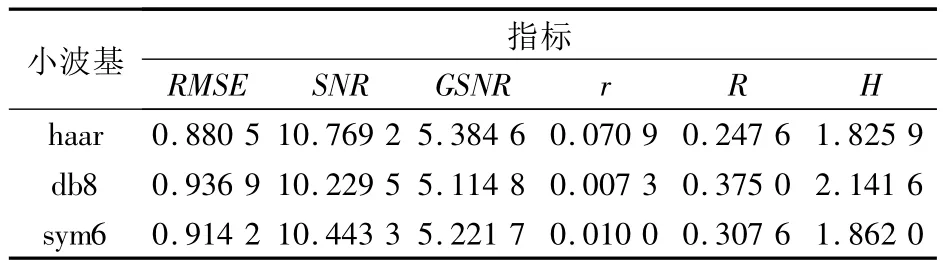
表1 6种评价方法对不同小波基去噪结果的评价结果(分解层数为5)Tab.1 Evaluation of different wavelet denoising results with six evaluation methods

采用上述策略对包含噪声较少的信号B2进行分析，发现采用haar小波基，分解层数为4时效果最佳。图3展示了haar小波基对信号B2进行分解后，各评价指标的评价结果。可见，没有一种方法可以正确确定分解与重构层次，其评价结果的特征与B1类似。

表2展示了分解层数为4时，6种评价方法针对haar、db8和sym6 3种小波基对信号B2去噪结果的评价。可见:1)RMSE、SNR、GSNR及H 4种方法得到正确的结论;2)r和R方法无法得到正确结论。

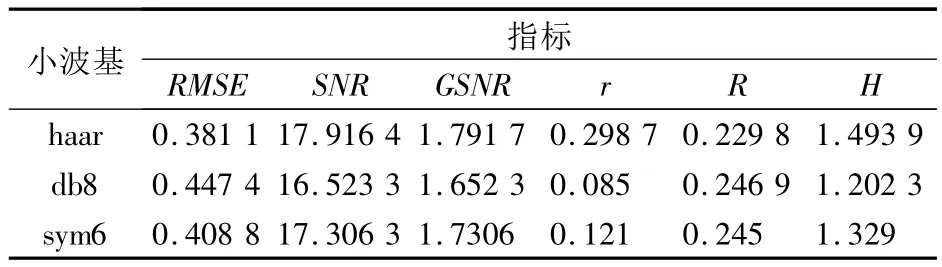
表2 6种评价方法对不同小波基去噪结果的评价结果(分解层数为4)Tab.2 Evaluation of different wavelet denoising results with six evaluation methods

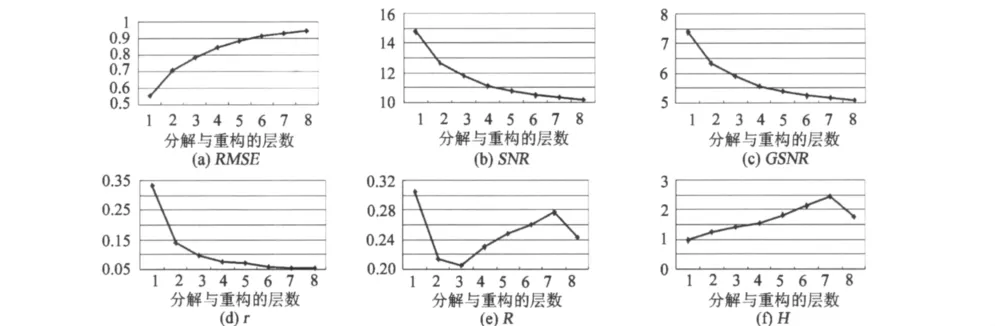
图2 6种评价方法对信号B1去噪结果的评价结果(haar小波基)Fig.2 Evaluation results of B1(haar)signal denoising results with six evaluation methods

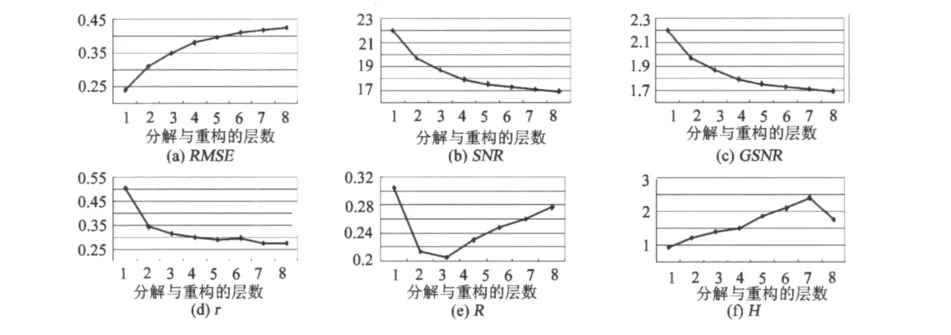
图3 6种评价方法对信号B2去噪结果的评价结果(haar小波基)Fig.3 Evaluation results of B2(haar)signal denoising results with six evaluation methods

4.3 模拟变形监测数据实验分析

采用与4.2节类似的分析思路，发现采用db8小波基对S1进行分解，当分解层数为4时，得到的为最佳结果。图4展示了db8小波基对信号B1进行分解后，各评价指标的评价结果。分析发现，没有一种指标可以准确识别正确的分解层次，虽然R和 H方法出现极值点，但其指示结果是错误的。

表3展示了分解层数为4时，6种评价方法针对haar、db8和sym6 3种小波基对信号S1去噪结果的评价。可见:1)RMSE、SNR、GSNR及r 4种方法得到了正确结论;2)H和R方法无法得到正确结论。

对于包含较少噪声的信号S2，采用db8小波基，分解层数为3时，去噪效果最好。5种评价指标的评价结果列于图5。从中可见:现有的各种评价指标，无法确定分解层数为3时去噪结果最佳。

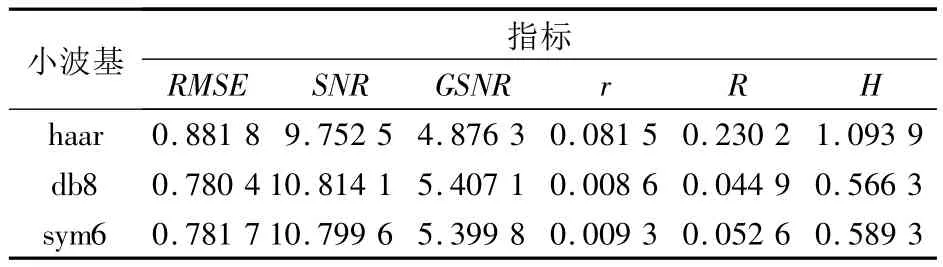
表3 6种评价方法对不同小波基去噪结果的评价结果(分解层数为4)Tab.3 Evaluation of different wavelet denoising results with six evaluation methods

表4展示了分解层数为3时，5种评价方法针对haar、db8和sym6 3种小波基对信号S2去噪结果的评价。可见只有RMSE、SNR、GSNR以及H 4种指标可以识别正确结果，其他方法均无法得到正确的结论。

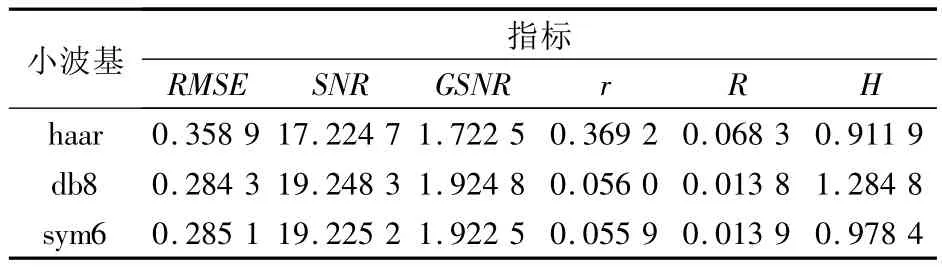
表4 6种评价方法对不同小波基去噪结果的评价结果(分解层数为3)Tab.4 Evaluation of different wavelet denoising results with six evaluation methods

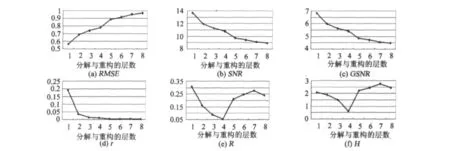
图4 6种评价方法对信号S1去噪结果的评价结果(db8小波基)Fig.4 Evaluation of S1(db8)signal denoising results with six evaluation methods

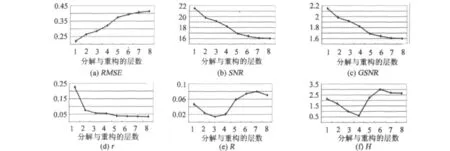
图5 6种评价方法对信号S2去噪结果的评价结果(db8小波基)Fig.5 Evaluation of S2(db8)signal denoising results with six evaluation methods

4.4 结果分析

1)现有的小波去噪质量评价方法在指导选择最佳的分解层次方面的能力非常欠缺，从实验结果可以看出没有一种方法可以得到正确的结论。其中6种具体的评价指标大致可以分为两种类型:(1) RMSE、SNR、GSNR3种方法对于未完全去噪的情况比较敏感，且评价结果的变化是单调的，没有明显的峰值出现;(2)r、R和H3种方法对过度去噪的情况比较敏感，其中r、R方法评价结果的变化也是单调的，H方法的评价结果虽然有峰值，但其结果的可靠性不高。

2)针对同一信号采用不同小波基去噪，现有评价指标的评价能力存在差异。其中RMSE、SNR和GSNR方法通常能够得到合理的评价结果;而r、R以及H方法的评价效果很不稳定，可靠性差。

3)分析各种评价方法的表现性能可以发现: (1)RMSE、SNR及GSNR方法在未完全去噪时结果更符合定义，难以对一个信号不同层次的去噪效果进行评价，但其对于采用不同小波基对信号进行去噪的结果的质量评价在现有方法中是最可靠的，可以在实际应用时，作为最佳小波基选择的依据;(2) r、R与H方法的可靠性较差，倾向于识别过度去噪的情况，建议在实际应用中不要单独使用。

5 结语

研究了现有小波去噪质量评价方法的实际表现，给出了现有评价方法针对单一信号不同分解层次去噪结果及不同小波基去噪结果的实际应用效果。同时，得到了现有评价方法的基本评价规律。实验分析发现，现有方法很难满足实际应用的要求，尤其是用于辅助选取单一信号最佳去噪结果方面存在较大的缺陷。同时也证明，基于经典统计学的质量评价方法在小波分析去噪这类基于非统计理论的数据处理方法中的应用，存在较大的局限。

1 宁津生，汪海洪，罗志才.小波分析在大地测量中的应用及其进展［J］.武汉大学学报(信息科学版)，2004，29 (8):659-663.(Ning Jinsheng，Wang Haihong and Luo Zhicai.Applications of wavelet analysis in geodesy and its progress［J］.Geomatics and Information Science of Wuhan University，2004，29(8):659-663)

2 黄声享，刘经南.GPS变形监测系统中消除噪声的一种有效方法［J］.测绘学报，2002，31(2):104-107.(Huang Shengxiang and Liu Jingnan.A novel method for reducing noises in GPS deformation monitoring system［J］.Acta Geodaetica et Cartographica Sinica，2002，31(2):104 -107)

3 黄声享，刘经南.小波分析在高层建筑动态监测中的应用［J］.测绘学报，2003，32(2):153-157.(Huang Shengxiang and Liu Jingnan.Deformation analysis based on wavelet and its application in dynamic monitoring for highrise buildings［J］.Acta Geodaetica et Cartographica Sinica，2003，32(2):153-157)

4 黄丁发，卓建成.GPS相位观测周跳检测的小波分析法［J］.测绘学报，1997，26(4):352-357.(Huang Dingfa and Zhuo Jiancheng.Wavelet analysis for cycle slip detection and reconstruction of GPS carrier phase measurement［J］.Acta Geodaetica et Cartographica Sinica，1997，26(4):352 -357)

5 何永红，文鸿雁.第二代小波在GPS双差观测值消噪中的应用［J］.大地测量与地球动力学，2010，(3):92-95.(He Yonghong and Wen Hongyan.Application based on second-generationwavelet in signal de-noising of GPS double difference observations［J］.Journal of Geodesy and Geodynamics，2010，(3):92-95)

6 张燕，吴云.GPS时间序列揭示地震前兆的初步探索［J］.大地测量与地球动力学，2005，(3):96-99.(Zhang Yan and Wu Yun.Preliminary discussion on GPS time series manifesting earthquake precursor［J］.Journal of Geodesy and Geodynamics，2005，(3):96-99)

7 王中宇，夏新涛，朱坚民.非统计原理及其工程应用［M］.北京:科学出版社，2005.(Wang Zhongyu，Xia Xintao and Zhu Jianmin.Statistical principle and its application in engineering［M］.Beijing:Science Press，2005)

8 程正兴，杨守志，冯晓霞.小波分析的理论、算法、进展与应用［M］.北京:国防工业出版社，2007.(Cheng Zhengxing，Yang Shouzhi and Feng Xiaoxia.Theory，algorithms and applications of wavelet analysis［M］.Beijing:National Defense Industry Press，2007)

9 文鸿雁.基于小波理论的变形分析模型研究［D］.武汉大学，2004.(Wen Hongyan.A study of deformation analysis model based on wavelet theory［J］.Wuhan:Wuhan University，2004)

10 吴富梅，杨元喜.基于小波阈值消噪自适应滤波的GPS/INS组合导航［J］.测绘学报，2007，36(2):124 -128.(Wu Funei and Yang Yuanxi.GPS/INS integrated navigation by adaptive filtering based on wavelet threshold de-noising［J］.Acta Geodaetica et Cartographica Sinica，2007，36(2):124-128)

11 吴继忠.GPS观测数据的小波阈值法消噪［J］.大地测量与地球动力学，2009，(4):79-82.(Wu Jizhong.De -noising of GPS observations with wavelet threshold method［J］.Journal of Geodesy and Geodynamics，2009，(4): 79-82)

12 陈强，黄声享.小波去噪效果评价的另一指标［J］.测绘信息与工程，2008，33(5):13-14.(Chen Qiang and Huang Shengxiang.An evaluation indicator of wavelet denoising［J］.Journal of Geomatics，2008，33(5):13-14)

13 李宗春，等.变形测量异常数据中的小波变换最佳级数的确定［J］.武汉大学学报(信息科学版)，2011，36 (3):285-288.(Li Zongchun，et al.Deformation measurement of abnormal data in the wavelet transform to determine the best series［J］.Geomatics and Information Science of Wuhan University，2011，36(3):285-288)

14 赵瑞珍，等.基于稀疏表示的小波去噪［J］.中国科学(E辑:信息科学)，40(1):33-40.(Zhao Ruizhen，et al.Wavelet denoising based on sparse representation［J］.Science China Information Sciences，40(1):33-40)

A COMPARATIVE STUDY ON VALIDITY ASSESSMENT OF WAVELET DE-NOISING

Tao Ke and Zhu Jianjun
(Department of Geomatics Engineering，Central South University，Changsha 410083)

Wavelet transform has played an important role in the field of surveying data processing，as the noise can be eliminated effectively on the basis of wavelet decomposition and reconstruction.Currently，the research of wavelet de-noising mainly focuses on the development of wavelet de-noising methods，however，the validity assessment of wavelet de-noising result should be indeed taken into account.Seeing that，a comparative study on validity assessment methods of wavelet de-noising is down.The practical performance of existing validity assessment methods is obtained through a series of experiments.

wavelet transform;wavelet de-noising;validity assessment;surveying data;data processing

1671-5942(2012)02-0128-06

2011-12-08

国家自然科学基金(40974007)

陶珂，女，1987年生，硕士研究生，主要从事大地测量数据处理方面研究.E-mail:hncstaoke@126.com

P207

A