溢洪道挑流鼻坎水气二相流数值模拟研究

穆 亮，高学平

(天津大学建筑工程学院，天津300072)

在各种泄洪消能方式中，采用较多的是挑流消能。在挑流消能布置中，挑流鼻坎的体型是决定消能效果的控制因素之一。工程中常用的挑坎形式主要有顺直挑坎、横向扩散挑坎、窄缝挑坎和差动式挑坎等，其中，横向扩散挑坎、窄缝挑坎和差动式挑坎主要是促使水舌沿横、竖向拉开［1］。

本文采用VOF方法、立方体网格、紊流模型模拟了某溢洪道三维流场，对溢洪道挑流鼻坎形式及水力特性进行了研究，为挑流鼻坎设计及优化提供了依据。

1 研究对象

某溢洪道工程设计洪水按100年一遇取值，泄洪流量1 290 m3/s，对应单宽流量45.8 m3/(s·m);校核洪水按1 000年一遇取值，泄洪流量1 950 m3/s，对应单宽流量69.3 m3/(s·m)。原设计方案为高低式挑流鼻坎，如图1(a)，优化方案为在原方案低坎处设置差动齿，将高坎中部高程降低，形成共5个齿槽，齿槽均成窄缝出流，收缩比采用0.25，如图1(b)。

2 控制方程及边界条件

2.1 控制方程

VOF(Volume of Fluid)法［2，3］是求解不可压缩、黏性、瞬变和具有自由面流动流体的一种数值方法，适用于2种或多种互不穿透流体间界面的流体的跟踪计算。模型对每一相引入体积分数变量αq，通过求解每一控制单元内体积分数值确定相间界面。设某一控制单元内第q相体积分数为αq(0≤αq≤1)。则αq=0时，控制单元内无第αq相流体;αq=1时，控制单元内充满第q相流体;0＜αq＜1时，控制单元包含相界面。每个控制单元内各相体积分数之和等于1。

引入VOF模型的k-ε紊流模型基本控制方程［4］如下:

(1)连续性方程

图1 某溢洪道立体效果图Fig.1 Three-dimensional renderings of a spillway

(2)动量方程

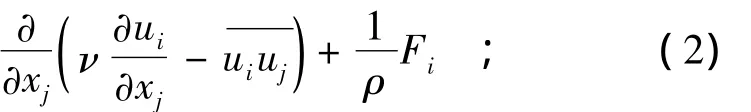
(3)k方程

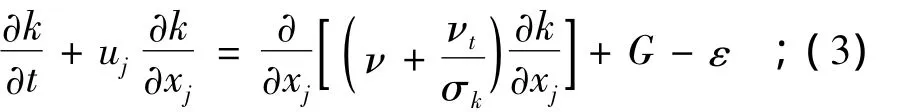
(4)ε方程

(5)体积分数方程

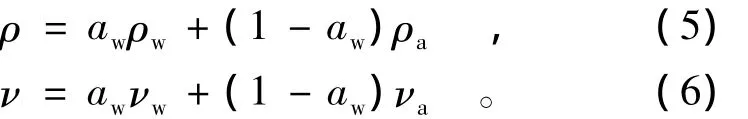
计算中所有控制单元表面体积通量的计算采用隐式差分格式，即

式中:n+1为当前时间步指示因子;n为前一时间步指示因子;αq，f为单元表面第q相体积分数计算值;V为控制单元体积;Uf为控制单元表面体积通量。

2.2 求解方法

模型求解采用有限体积法［5］，压力－速度耦合采用压力校正法，离散方程求解采用GMRES法，时间差分采用全隐格式。

2.3 网格划分及边界条件

上游距拱坝前缘200 m断面为进流边界，下游距电站尾水出口250 m为出流边界，上游进流边界和下游出流边界均按静水压强给出;固体边界采用无滑移条件;液面为自由表面。

溢洪道、上游库区和下游河道均采用立方体网格，溢洪道网格尺寸0.5 m，上游库区和下游河道网格尺寸分别为2 m和1 m，共约160×104，图2为网格模拟后坝体体型。

图2 网格模拟后溢洪道体型Fig.2 Spillway shape by grid simulation

3 计算结果及分析

挑流消能流态相对较为复杂，挑射水流受挑坎体型影响，出坎水舌形成大曲率水气交界面，气液掺混强烈，属于强非线性典型水气二相流问题。

3.1 挑射水舌

表1和图3为原设计方案与优化方案在1 000年一遇工况下水舌流态的对比。原设计方案:因溢洪道体型为径向集中式，高坎和低坎水舌在空中碰撞，合成一股水舌落入水垫塘，落点集中，水舌在纵向和横向上分布范围均相对较小。优化方案:水流经过窄缝式挑坎时，水流受收缩边墙的影响，沿横向收缩，沿纵向扩展;水体流过收缩段后，水舌竖向拉伸更充分，水舌入水较分散，掺气更为充分;经差动式挑坎作用，两侧低坎和中间高坎形成3股水舌，使水舌入水时在纵向上分布范围更大;同时横向上也减弱了因溢洪道径向集中式体型导致横向分布范围较小的影响，消除了水舌落点集中现象。

表1 溢洪道挑射水流特性Table 1 The hydraulic characteristics of nappe

3.2 水舌掺气扩散分析

图4给出了1 000年一遇工况下原设计方案和优化方案挑射水舌坝中轴线铅直剖面速度矢量及等值线图。图5为原设计方案和优化方案挑射水舌坝中轴线铅直剖面水体体积分数等值线图。图中将挑射水舌分成几个主要流速区:水舌主流上挑区(Ⅰ区)、水舌空中扩散掺气区(Ⅱ区)、水舌下落散裂掺气区(Ⅲ区)。Ⅰ区水流较为集中，出坎速度最高约为22m/s，且数值模拟结果显示此处核心区内体积分数αq均大于0.9，说明水舌基本没有掺气;随着水舌向上运动，位能逐渐增加，Ⅱ区水流速度相对较小，水舌竖向上逐渐扩散，水流掺气逐渐增大，水舌流速降低至最小，计算结果表明最低流速并没有出现在水舌的最高点，而是在最高点下游，此时水体扩散较为明显，与文献［6］结论一致。Ⅲ区中水体在重力作用下进一步扩散，流速逐渐增加，水体全部掺气，在入水前流速增至最大。

与原设计方案相比较，优化方案水流空中扩散范围更大，掺气更加充分，入水前水舌的水体体积分数相对较小，同时优化方案水舌入水速度为26m/s左右，小于原设计方案水舌入水速度。

应当指出，文中在k-ε紊流模型中采用VOF方法跟踪自由水面，该方法是基于水体不破碎、水气间无混杂存在的假设。而挑坎处的水流速度较快，有大量的水气混杂、水体的破裂及气体的掺入，水体和气体的掺混是在微观尺度上的，空气与下泄水舌的交界面上会产生空气漩涡和水漩涡，漩涡产生以后向外扩散，其扩散至距其发生点横向距离的远近是随机的，用该方法不能完全模拟实际挑射水舌掺气问题。但是，从本文水舌挑距的数值模拟结果与模型试验数据对比以及文献［1］的研究成果来看，说明用该方法模拟挑流水舌掺气问题在一定程度上能反映出水流实际运动的掺气效果。

图3 溢洪道挑射水舌流态Fig.3 Flow patterns of nappe before and after optimization

图4 挑射水舌坝中轴线铅直剖面速度矢量及等值线Fig.4 Velocity vectors and isolines of nappe in the profile of dam central axis

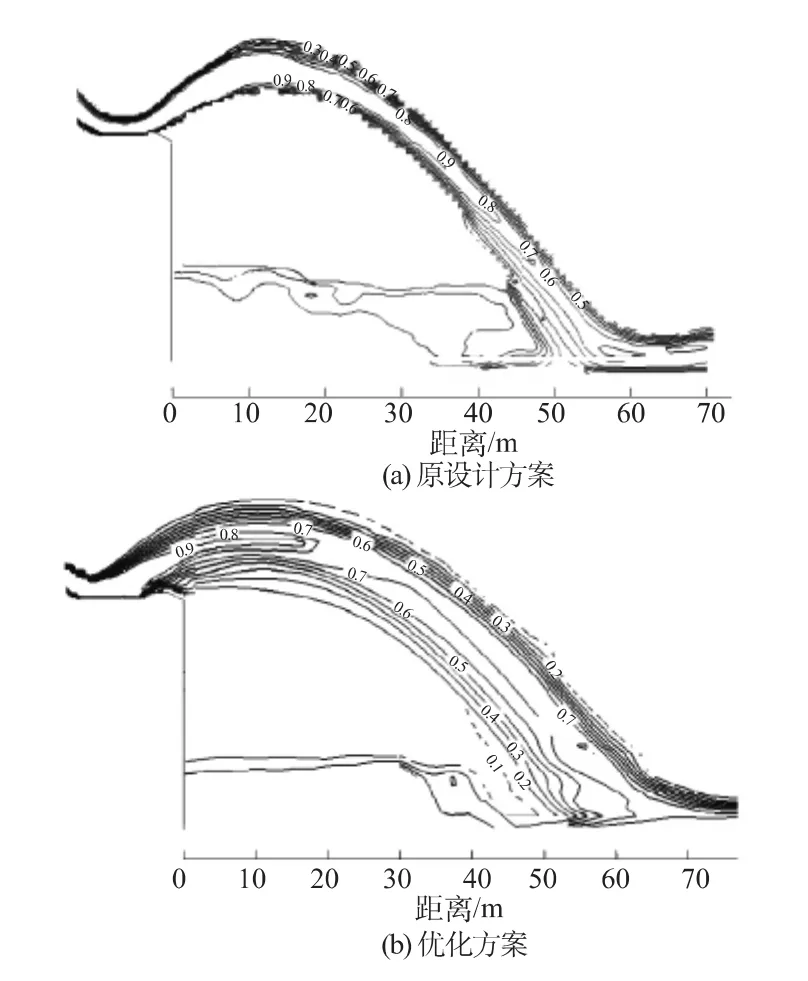
图5 挑射水舌坝中轴线铅直剖面水体体积分数等值线Fig.5 Isolines of water volume fraction of nappe in the profile of dam central axis

3.3 底板压强

表2为原设计方案与优化方案在1 000年一遇工况下水垫塘底板压强的对比。原设计方案水舌入水点位于0+096至0+105.7，优化方案水舌入水点位于0+93.9至0+110.3。0+077 至 0+087 处于水舌入水点上游，2种方案在此处的底板压强值相差不大。原设计方案由于高、低坎两股水舌在空中碰撞后合成一股水舌落入水垫塘，导致水垫塘内0+107至0+117附近压强值较大，最大值达329.5 kPa;优化方案水舌分散，无明显集中现象，在0+107至0+127附近压强值相对较高，最大值为255.7 kPa。水舌入水后，在其下游引起壅水，两方案水垫塘底板压强最大值均发生在水深最大处。

同时，对优化方案进行了物理模型试验验证，模型按重力相似准则进行设计，采用正态模型，模型比尺为λL=50。表2中给出了优化方案不同测点水垫塘底板压强计算值和试验值。二者数值吻合较好，基本规律一致，说明本文方法能较好地模拟溢洪道挑射水流的水力特性。

表2 水垫塘底板压强Table 2 Pressure intensities on plunge pool slab

3.4 河道流速

表3为原设计方案与优化方案在1 000年一遇工况下0+155断面流速分布的对比。数据对比可知，原设计方案流速明显高于优化方案，原设计方案0+155断面处流速最大值为17.10m/s，优化方案流速最大值为14.66m/s。主要由于原设计方案挑射水流落点集中，空中掺气不充分，下泄水流能量较高，造成下游河道内流速较大，优化方案水舌落点较为分散，水流掺气消能充分，落入水垫塘后水体能量较小。

表3同时给出了河道0+155断面处流速优化方案计算值和试验值，二者数值吻合较好，基本规律一致。

表3 河道0+155断面流速Table 3 Velocities in profile 0+155

4 结论

(1)应用VOF方法、k-ε紊流模型，对某溢洪道挑射水流的水力特性进行了三维数值模拟研究，数值模拟结果得到了物理模型试验的验证，计算值与试验测量值吻合较好，说明所采用的方法能较好地模拟溢洪道挑射水流的水力特性。

(2)应用数值模拟方法可较为方便地得出水体剖面水力特性分布，对挑射水舌铅直剖面速度矢量及等值线图进行分析，表明水舌最低流速并不在水舌顶点处，而是在顶点下游不远处。同时，数值模拟计算可较为方便地得出水体掺气情况。

(3)计算表明，将某溢洪道由原高低式挑流鼻坎修改为差动式挑流鼻坎后，使下泄水流入水范围增大，提高了挑流消能的消能效率，减小了水垫塘底板压强，降低了下游河道水流流速。

［1］刁明军，杨永全，王玉蓉，等.挑流消能水气二相流数值模拟［J］.水利学报，2003，(9):77－82.(DIAO Ming-jun，YANG Yong-quan，WANG Yu-rong，et al.Numerical Simulation of Water-Air Two-Phase Jet Flow from Flip Bucket to Plunge Pool［J］.Journal of Hydraulic Engineering，2003，(9):77－82.(in Chinese))

［2］李 玲，陈永灿，李永红.三维VOF模型及其在溢洪道水流计算中的应用［J］.水力发电学报，2007，26(4):83－87.(LI Ling，CHEN Yong-can，LI Yonghong.Three Dimensional VOF Model and Its Application to the Water Flow Calculation in the Spillway［J］.Journal of Hydroelectric Engineering，2007，26(4):83－87.(in Chinese))

［3］高学平，叶 飞，宋慧芳.侧式进/出水口水流运动三维数值模拟［J］.天津大学学报，2006，39(5):518－522.(GAO Xue-ping，YE fei，SONG Hui-fang.3D Numerical Simulation on the Flow in Side Inlet/Outlet［J］.Journal of Tianjin University，2006，39(5):518－522.(in Chinese))

［4］王福军.计算流体动力学分析［M］.北京:清华大学出版社，2004.(WANG Fu-jun.Computational Fluid Dynamics Analysis［M］.Beijing:Tsinghua University Press，2004.(in Chinese))

［5］HORT C W，NICHOLS B D.Volume of Fluid(VOF)Method for the Dynamics of Free Boundaries［J］.Journal of Computational Physics，1981，39(2):201－225.

［6］刘宣烈，张文周.空中水舌特性研究［J］.水力发电学报，1988，(2):46－54.(LIU Xuan-lie，ZHANG Wenzhou.The Investigation of Dynamic Characteristics of Jetflow in Open Air［J］.Journal of Hydroelectric Engineering，1988，(2):46－54.(in Chinese))