大规模电网的动态无功优化算法

赖永生， 刘明波， 陈燕梅

(1.福建电力调度控制中心， 厦门 361004； 2.华南理工大学电力学院， 广州 510640；3.福建省厦门电业局， 厦门 361004)

大规模电网的动态无功优化算法

赖永生1， 刘明波2， 陈燕梅3

(1.福建电力调度控制中心， 厦门 361004； 2.华南理工大学电力学院， 广州 510640；3.福建省厦门电业局， 厦门 361004)

为解决应用内嵌离散惩罚的非线性原对偶内点法求解离散整数动态无功优化模型时产生的“维数灾”问题，对修正方程用块矩阵解耦的算法做进一步探讨，提出了两次求解修正方程系数矩阵并三角分解从而降低动态无功优化应用于大电网时的数据存储量的新思路，即以时间换取空间(定义为时空转换)。在两个实际系统(14节点和538节点系统)和IEEE 118节点系统上的优化计算表明，所提算法既能计算大电网的动态无功优化，又具有较快的计算速度。

大电网； 动态无功优化； 块矩阵结构； 精确解耦； 时空转换

完整的动态无功优化模型是计及设备动作次数约束，并考虑变量离散化特性的一种非线性混合整数规划问题，在实际运行电网特别是大电网中计算动态无功优化问题比较困难，求解比较复杂。

迄今，国内外学者已提出许多求解配电网电压无功控制问题的计算方法。文献[1，2]先对网损曲线进行分段，并对对应的负荷曲线根据变化的剧烈程度进行划分，从而把动态优化等效成若干个时段的静态优化。该算法要求设备动作具有同时性。文献[3，4]把离散设备动作次数作为调节代价加入目标函数中，从而将各时段解耦。该算法具有较快的计算速度，但离散设备的调节代价是根据经验得到。文献[5]对24时段进行静态无功优化后，根据优化结果设置调节设备的预动作表，并根据此动作表把24时段耦合动态无功优化解耦，并用基于隔离小生境遗传算法求解，该方法模型简单，便于实现，但预动作表的设置不能保证得到全局最优解。文献[6～11]采用动态规划法或混合法求解。动态规划法可以得到全局最优解，但在离散设备数量或允许动作次数增加时会使问题的求解规模变得很大而难以求解。文献[12]将模糊集理论应用于配电网络动态无功优化的建模，该模型考虑了有载调压变压器分接头和电容器组的动作次数限制，并采用模拟退火算法进行求解。文献[13～15]提出了完整的动态无功优化数学模型和严格数学意义下的优化算法，该算法存在“维数灾”的难题，随着系统规模的扩大而急剧增加的计算负担可能会引起计算速度太慢甚至是数值精度的问题，限制了其在大型电力系统中的应用。文献[16]提出了一种基于近似牛顿方向的动态无功优化解耦分解算法，该算法如何找到适合的“预处理”是个难题，且不能在理论上确定m的取值也导致该法的实用性差。文献[17]在分析修正方程特点的基础上，提出用块矩阵对修正方程进行精确解耦，具有较快的计算速度，但其数据存储量大，在计算大规模电网时仍会出现“维数灾”问题。

本文在文献[17]的基础上，对修正方程用块矩阵解耦的算法做进一步的探讨，提出两次求解修正方程系数矩阵并三角分解从而降低动态无功优化应用于大电网时的数据存储量的新思路。本文算法由于两次求解修正方程系数矩阵并三角分解，计算效率会降低，但可降低数据存储量，也即用时间换取空间(定义为时空转换)实现大规模电网的动态无功优化。所提算法既能计算大规模电网的动态无功优化近最优离散解，又具有较高的计算效率。

1 动态无功优化模型及其解耦算法

设系统有n个节点、u台有载调压变压器、m台可调发电机，有r个节点装设可投切电容器组；并将全天等分为24个时段(t=0，1，2，…，23)，从而将各负荷母线的全天有功和无功变化曲线分为24段，并认为各时间段中的负荷功率保持恒定。本文采用的动态无功优化模型和基本算法与文献[13]一致，最终得到修正方程[13]为

(1)

式中：A(t,t)为对称矩阵，At,t∈R[(p+q+3n)×(p+q+3n)]；

以上详细的求解过程参见文献[13]。从式(1)可以看出，修正方程系数矩阵具有箭形分块结构，可采用文献[17]中的解耦算法2的形式，最终将式(1)展开后相继求解方程为

(2)

A(t,t)Δz(t)=b(t)-A(t,n)Δyn

(3)

即由式(2)求出Δyn，然后代入式(3)求得Δz(t)，从而求得式(1)。

2 时空转换算法的流程及实现

其中，SUB1为求解24个时段的A(t,t)矩阵子程序；SUB2为求解式(2)子程序；SUB3为求解式(3)子程序。该算法流程用TH1表示。

对上述流程再进一步分析，在SUB1中仍需对求出的24个时段的A(t,t)矩阵进行存储，所存储数据量也可能限制动态无功优化在大电网中的应用，本文再次采用时空转换算法解决24个时段的A(t,t)矩阵存储问题，也即把SUB1中求解24个时段的A(t,t)矩阵的过程并入至SUB2与SUB3，即在SUB2与SUB3分别各自求A(t,t)矩阵。由于A(t,t)矩阵的维数为 维，从而24个时段的A(t,t)矩阵所需存储元素个数仅为(p+q+3n)×(p+q+3n)个。此时算法流程为

其中，SUB4为计算式(2) 子程序，SUB5为计算式(3) 子程序。该流程算法用TH2表示。

3 算例分析

3.1 试验系统简介

为验证所提算法的正确性和有效性，采用1个个试验系统和2个实际系统作为算例。其中系统1与系统2分别为文献[17]的一个实际14节点系统和IEEE118节点系统。系统3为文献[18]中的某省级538节点实际系统。所有参数均为标幺值，基准功率为100 MVA。

系统3为某省级538节点系统，该系统节点数为538，有48台发电机，118个无功补偿设备，409条变压器支路。考虑到该电网节点众多、某些重要节点的运行参数要求严格等特点，选择了48台发电机、118个无功补偿设备、51台升压变压器和13台降压变压器参与优化。可调变压器变比、无功补偿设备和发电机无功出力的上、下限均按系统的给定值确定，可调变压器的变比和分级步长按变压器的铭牌值给定，有2.25%、2.5%、1.25%和1.5%。无功补偿设备的分级步长都取为0.05。节点电压的上、下限根据实际电网中节点性质的不同确定了几种范围：对于发电机机端电压和500 kV母线电压、500 kV变电站的220 kV电压监测点和220 kV电厂的220 kV电压监测点，其电压允许偏移值严格限定为1～1.1；对于220 kV变电站的220 kV电压监测点，其电压允许偏移值为0.95～1.10；其余节点电压的上、下限定为0.90～1.15。日负荷特性曲线与文献[17]的典型日负荷曲线一致，将154个负荷归为这6个负荷类别。

3.2 试验结果分析

对3个试验系统，分别采用本文算法TH1和TH2与文献[17]的解耦算法2进行对比计算，为方便说明，文献[17]解耦算法2用TH3表示。所有算法均用C语言编写，在Visual C++ 6.0环境编译。所用计算机为Intel(R) Core(TM) 2 Duo CPU T8100 2.1GHz，内存2GB。假设所有设备的全天最大允许动作次数均取相同值。

表1和表2分别列出TH3算法在不同的动作次数约束Cx1下计算试验系统1和试验系统2得到的全天能量损耗、迭代次数和计算时间，但由于内存不足，TH3不能够计算试验系统3。

表1 系统1由TH3计算得到的能量损耗、迭代次数和计算时间

表2 系统2由TH3计算得到的能量损耗、迭代次数和计算时间

表3和表4分别列出了TH1和TH2算法在不同的动作次数约束Cx1下计算试验系统1和试验系统2得到的全天能量损耗、迭代次数和计算时间。表中最后一部分“静态结果”为用24时段单时段静态优化算法[18]的计算结果(其中能量损耗和计算时间取24个时段之和，迭代次数取24个时段的平均值)。

从表3与表1、表4与表2的对比中发现，本文算法在能量损耗、迭代次数与TH3算法完全一致，但计算时间比TH3算法多，也即计算效率比TH3算法低，这是因为本文的两种算法均对A(t,t)矩阵进行了两次三角分解。其中，试验系统1中TH2算法计算效率比TH1算法计算效率稍低，试验系统2中TH2算法计算效率又比TH1高。

本文TH1和TH2算法均对A(t,t)矩阵三角分解结果不存储，节约了大量内存，因此可以计算试验系统3。对于系统3，改变其Cx1从20到110，发现Cx1取51次及以下时，均不能收敛。表5列出了系统3在不同Cx1下得到的全天网损、迭代次数和计算时间。

表3 系统1计算得到的能量损耗、迭代次数和计算时间

表4 系统2计算得到的能量损耗、迭代次数和计算时间

从表5可以看出，TH1和TH2算法的能量损耗和迭代次数均一致，但TH2的计算效率远远高于TH1。这充分说明对于大电网系统，采用两次求解A(t,t)矩阵并三角分解的时空转换算法能够节约大量的计算机内存且具有较快的计算速度，也即充分说明了本文算法的有效性。

本文还把计算机内存扩展到3.25G，尝试用TH3算法计算试验系统3，仍是内存不足导致无法计算；另外，把TH3算法24时段的A(t,t)矩阵采用只存储其上三角矩阵的办法，内存仍为3.25G，也是内存不足无法计算。这充分说明了本文算法在计算大电网动态无功优化数据存储量方面的优势，即充分说明了本文算法在计算大电网方面的有效性。

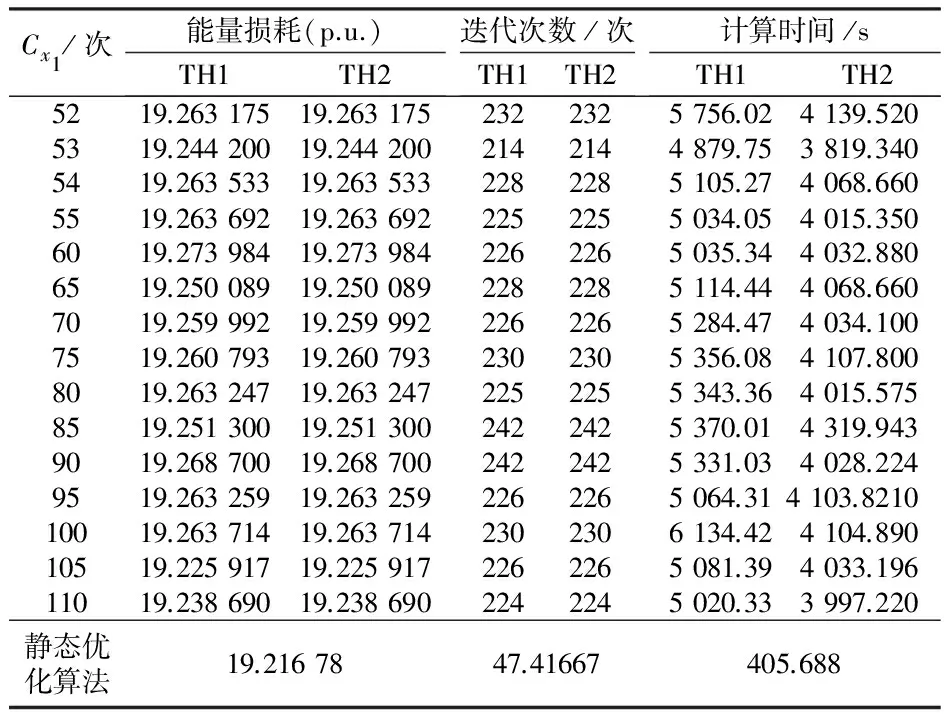
表5 系统3计算得到的能量损耗、迭代次数和计算时间

4 结论

(1)采用两次求解A(t,t)矩阵并三角分解的时空转换算法，虽会增加一定计算时间，但可以节省大量存储空间，取得了大规模电网的动态无功优化结果；

(2)TH1与TH2对A(t,t)矩阵采取不同的处理办法，TH2所需的存储空间比TH1少，对于大规模电网TH2计算效率也比TH1高。这是由于TH2中SUB4和SUB5分别求A(t,t)矩阵，此时定义A(t,t)矩阵变量为局部变量，且TH2的数据存储量较小，在计算大规模电网时，数据交换均在内存内部，从而计算效率高；而TH1只求解一次A(t,t)矩阵，定义A(t,t)矩阵变量为公用变量，且其所需的数据存储量也较大，在计算大规模电网时，可能会内存不足，此时有一部分数据存储于虚拟内存，导致在内存与虚拟内存之间进行数据交换，从而降低计算效率；所以TH2具有较快速度，并且随着计算系统规模的增大，TH2算法的计算效率及存储优势比TH1算法也更加明显。

[1] 邓佑满, 张伯明, 田田(Deng Youman，Zhang Boming，Tian Tian). 虚拟负荷法及其在配电网络动态优化中的应用(A fictitious load algorithm and its applications to distribution network dynamic optimizations) [J]. 中国电机工程学报(Proceedings of the CSEE)，1996, 16(4): 241-244.

[2] Chebbo A M , Irving M R , Sterling M J H. Reactive power dispatch incorporating voltage stability[J]. IEE Proceedings: Generation , Transmission and Distribution ,1992 ,139 (3) : 253-260.

[3] 张勇军,俞悦,任震,等(Zhang Yongjun , Yu Yue , Ren Zhen,etal). 实时环境下动态无功优化建模研究(Research on dynamic modeling for reactive power optimization under real-time circumstance) [J]. 电网技术(Power System Technology)，2004，28 (12) :12-15.

[4] 周任军,段献忠,周晖(Zhou Renjun ,Duan Xianzhong , Zhou Hui). 计及调控成本和次数的配电网无功优化策略(A strategy of reactive power optimization for distribution system considering control action cost and times) [J]. 中国电机工程学报(Proceedings of the CSEE),2005 ,25 (9) :23-28,157.

[5] 蔡昌春，丁晓群，王宽,等(Cai Changchun, Ding Xiaoqun, Wang Kuan,etal).动态无功优化的简化方法及实现(Simplified method of dynamic reactive power optimization and its implementation) [J].电力系统自动化(Automation of Electric Power Systems),2008,32(5):43-46,58.

[6] Hsu Y-Y，Kuo H-C. Dispatch of capacitors on distribution system using dynamic programming [J]. IEE Proceedings: Generation，Transmission and Distribution ,1993，140(6)：433-438.

[7] Lu Feng-Chang, Hsu Yuan-Yin.Fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation [J]. IEEE Trans on Power Systems ,1997,12(2)：681-688.

[8] Hsu Y Y, Lu F C. A combined artificial neural network-fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation [J]. IEEE Trans on Power Systems ,1998, 13(4):1265-1271.

[9] Hsu Yuan-Yin, Yang Chien-Chuen. A hybrid artificial neural network-dynamic programming approach for feeder capacitor scheduling[J]. IEEE Trans on Power Systems ,1994,9(2):1069-1075.

[10]Hsu Yuan-Yih，Lu Feng-Chang. A combined artificial neural network-fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation [J]. IEEE Trans on Power Systems ,1998,13(4):1265-1271.

[11]Liang R -H, Cheng C -K. Dispatch of main transformer ULTC and capacitors in a distribution system[J]. IEEE Trans on Power Delivery ,2001,16(4):625-630.

[12]Liang Ruey-Hsun， Wang Yung-Shuen. Fuzzy-based reactive power and voltage control in a distribution system [J]. IEEE Trans on Power Delivery ,2003,18(2)：610-618.

[13]刘明波，谢敏，赵维兴.大电网最优潮流计算[M].北京：科学出版社，2010.

[14]Sharif S S, Taylor J H. Dynamic optimal reactive power flow[C]∥The American Control Conference, Philadelphia, USA: 1998.

[15]Sharif S S, Taylor J H. Real-time implementation of optimal reactive power flow[C]∥The American Control Conference, San Diego, USA: 1999.

[16]Liu M B, Canizares C A, Huang W. Reactive power and voltage control in distribution systems with limited switching operations [J].IEEE Trans on Power Systems ,2009，24(2)：889-899.

[17]赖永生，刘明波(Lai Yongsheng, Liu Mingbo).电力系统动态无功优化问题的快速解耦算法(Fast decomposition algorithm for solution of dynamic reactive power optimization problem in power systems) [J].中国电机工程学报(Proceeding of the CSEE)，2008，28(7)：32-39.

[18]Liu Mingbo，Tso S K, Ying Cheng. An extended nonlinear primal-dual interior-point algorithm for reactive-power optimization of large-scale power systems with discrete control variables [J]. IEEE Trans on Power Systems ,2002，17(4)：982-991.

赖永生(1981-)，男，硕士，工程师，研究方向为电力系统无功优化调度与电压控制。Email:laiysh16@126.com

刘明波(1964-)，男，教授，博士生导师，研究方向为电力系统优化、运行与控制。Email:epmlliu@scut.edu.cn

陈燕梅(1983-)，女，学士，助理工程师，主要从事调控一体化工作。Email:yanmei831244@126.com

AlgorithmforDynamicReactivePowerOptimizationProbleminLargePowerGrid

LAI Yong-sheng1， LIU Ming-bo2， CHEN Yan-mei3

(1.Fujian Electric Power Dispatching Control Center, Xiamen 361004, China；2.School of Electric Power Engineering, South China University of Technology,Guangzhou 510640, China；3.Xiamen Power Supply Bureau, Xiamen 361004, China)

In order to resolve the so-called problem of quot;curse of dimensionalityquot;, this paper analyzed dynamic reactive-power optimization by using nonlinear primal-dual interior-point algorithm which introduced discretization penalty and showed the further exploration of block-matrix decoupling method used in the coefficient matrix of the reduced linear correction equation. Moreover, a realization of exchanging time for space (time-space transformation) by twice computing coefficient matrix of the reduced linear correction equation and its triangular factorization which can reduce the data storage is given. The numerical results on IEEE 118-bus system and two real power supply systems with 14 nodes and 538 nodes show that the proposed algorithm is suitable for using in large-scale power systems and has fast calculation speed.

large-scale power system； dynamic reactive power optimization； block matrix structure； accurate decomposition； time-space transformation

TM744

A

1003-8930(2012)05-0007-06

2011-08-24；

2011-10-12

国家自然科学基金项目(50777021)