矢量距浓度免疫算法在配电网重构中的应用

李 樊， 刘天琪， 李兴源， 江东林

(四川大学电气信息学院， 成都 610065)

矢量距浓度免疫算法在配电网重构中的应用

李 樊， 刘天琪， 李兴源， 江东林

(四川大学电气信息学院， 成都 610065)

针对免疫算法在配电网重构中收敛速度慢，易收敛到局部最优解等问题，提出矢量距浓度免疫算法。抗体的亲和度决定它的矢量距，并由矢量距得出抗体的浓度、选择概率和期望繁殖率，根据选择概率自适应调整抗体的变异率，根据期望繁殖率进行克隆操作以保证抗体的多样性和全局最优解的生成，最后结合疫苗接种和免疫记忆机制促进全局最优解的生成。算例结果表明，该算法能有效提高收敛速度和保证全局最优解的生成。

矢量距浓度免疫算法； 配电网重构； 变异； 克隆； 疫苗接种； 免疫记忆

配电网重构作为配电系统经济运行、自动控制的一个重要问题已被广泛关注。它是在满足系统约束条件的前提下，通过调整网络中分段开关和联络开关的开闭来寻求一种符合某特定运行要求的拓扑结构。

配电网络重构是多目标非线性混合优化问题，目前见诸于文献的方法主要有：①数学优化方法，如分支定界法[1]，但其存在严重维数灾问题；②启发式方法，如支路交换法[2]、最优流模式算法[3]，但它们缺乏数学意义上的全局最优性；③人工智能算法，如神经网络法[4]、蚁群算法[5，6]、粒子群算法[7，8]、遗传算法[9，10]、免疫算法[11～13]，这类算法虽能以较大的概率收敛到全局最优解，但也偶尔陷入局部最优。免疫算法具有良好的鲁棒性、灵活性、编码简单易行等特点，特别适合组合优化问题的求解，从而得到了较多的应用。但部分免疫算法放弃了浓度控制操作而易陷入局部最优，有的免疫算法进行浓度控制能防止陷入局部最优，但是它们采用的基于信息熵或欧氏距离的浓度控制都具有计算复杂，算法收敛速度慢等缺点。

为了解决上述问题，本文采用矢量距浓度免疫算法用于配电网重构，根据矢量距概念计算各个可行解抗体在集合中的距离、浓度、选择概率和期望繁殖率，将自适应的思想揉进免疫算法并根据抗体的选择概率调整可行解的变异率，通过由期望繁殖率决定的克隆操作来保证抗体的多样性和收敛速度之间的平衡，再结合疫苗接种和免疫记忆机制使改进后的免疫算法能快速准确地收敛到全局最优点。利用一实际69节点配电系统对算法进行了验证，证明其可行有效。

1 配电网重构的数学模型

本文选择网损最小作为目标函数，其表达式为

(1)

式中：N为系统支路总数；i为支路编号；ki为支路i开关的状态变量，0代表打开，1代表闭合；ri为支路i的电阻；Pi、Qi分别为支路i流过的有功功率和无功功率；Ui为支路i的末端节点电压。在网络重构过程中，还必须满足以下约束。

(1)等式约束，Pi、Qi、Ui必须满足潮流方程的等式约束条件，即

f(Pi，Qi，Ui)=0

(2)

(2)不等式约束，包括电压约束和支路过载约束等，即

Ui,min≤Ui≤Ui,max

(3)

Si≤Si,max

(4)

式中：Ui,min和Ui,max分别为节点电压下限和上限值；Si和Si,max分别为第i条支路的视在功率及线路容量。

(3)辐射型网络约束，必须保证配电网内无闭环、无孤岛。

2 用矢量距浓度免疫算法重构配电网

目前应用于配电网重构的一部分免疫算法没有进行抗体浓度控制而不能完全保证计算过程中解的多样性和全局最优解的生成，或者采用基于信息熵或欧氏距离进行抗体浓度控制，但是这两种浓度控制方法都具有计算数据量大、程序运行复杂和算法收敛速度慢等缺点。为此，本文提出了基于矢量距浓度控制的免疫算法。而且基本免疫算法应用到配电网重构时存在以下问题：①抗体经过交叉和变异操作后会生成大量的不可行解；②不合适的变异率可能使算法陷入局部最优。本文在基本免疫算法的基础上针对配电网运行要求放弃易产生不可行解的交叉操作并在变异操作中加入限制条件以减少不可行解的生成；利用自适应的思想根据抗体选择概率动态调整可行解的变异率以保证向全局最优解收敛。

本文将式(1)目标函数的倒数作为亲和度评估函数，从而抗体(解)的亲和度越大，表明抗体(解)越优，并采用前推回代法计算潮流，根据潮流结果求出抗体的亲和度。

2.1 矢量距浓度和期望繁殖率的定义

2.1.1 矢量距浓度的定义

由矢量距来计算抗体的浓度，不仅计算简单，而且也能很好地表示抗体浓度，所以本文采用矢量距法。矢量距浓度的定义如下[14]。

定义1在特定的、规模为N的非空免疫系统集合X中，抗体xi在集合X上的距离为

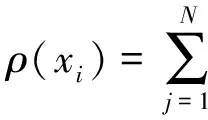
(5)

式中：f(xi)和f(xj)分别为抗体xi和xj的亲和度。

抗体xi的浓度为

(6)

与基于信息熵和欧氏距离的免疫算法相比，将抗体浓度直接对应于可行解抗体的亲和度函数f(xi)的定义具有缩小解群搜索空间，避免冗余计算信息重复运算等优点，从而加快算法的收敛速度。由式(6)可得基于抗体浓度的概率选择公式为

(7)

由式(7)知，集合X中与抗体i基因相似的抗体越少，抗体i被选中的概率就越大， 而与抗体i基因相似的抗体越多，抗体i被选中的概率就越小。根据抗体的选择概率来自适应调整它的变异率能使含有有效进化基因的低亲和度个体也可获得繁殖的机会。因此，基于矢量距的免疫算法在理论上保证了解的多样性。

2.1.2 期望繁殖率的定义

在免疫系统中，当抗体受到抗原刺激或者其他抗体刺激或抑制时，这种抗体的数量将发生变化。与抗原亲和力高的和浓度低的抗体将受到促进，反之，抗体受到抑制。这里引入期望繁殖率e(xi)来判定抗体的抑制和促进，并通过克隆操作来控制抗体浓度以保证抗体的多样性。

定义2在特定的、规模为N的非空免疫系统集合X中，抗体f(xi)期望繁殖率e(xi)为

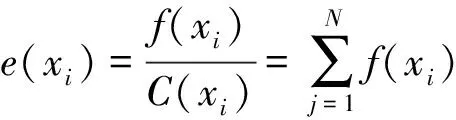
(8)

从式(8)可以看出，矢量距浓度免疫算法的期望繁殖率不仅与个体的亲和度有关，而且还与个体的浓度有关。

2.2 抗体编码和不可行解判定

本文选择二进制编码方式，为提高可行解在解空间中所占的比例，可限定断开开关的数目。同时为减小抗体长度，文献[15]给出的简化规则也应考虑：①不在任何环路内的开关必须闭合；②在网架结构合理的情况下，与电源相连的开关一般也应该闭合。在限定网络打开开关数量的基础上，应用一种基于最小生成树原理的网络全连通判定方法，即可完成对可行解的判定。

2.3 变异

2.3.1 可行解变异

根据可行解抗体的选择概率，采用自适应方法调整可行解的变异率为

(9)

式中：Pm为可行解变异率；Ps，max为可行解抗体选择概率最大值；Ps为需变异抗体的选择概率；Ps，ave为可行解抗体选择概率平均值；k为随机生成数。

采用自适应方法调整可行解的变异率可以使选择概率高的可行解变异率更低，以便于该抗体的保留，而对于选择概率低的抗体则相对应地采用高的变异率，便于更快地生成全局最优解。变异的方式为随机选择一位基因值为0的基因使它的值变为1，再随机选择另外一位基因值为1的基因使它的值变为0。这样可以使变异后的抗体保持断开开关数为m，减少了不可行解的产生。

2.3.2 不可行解变异

每次循环都会生成一部分不可行解，针对这部分不可行解可以采用全频率变异。变异操作仍以限定断开开关数目为原则，具体过程为根据断开开关数m，把不可行解平均分为m份，然后在分好的不可行解中随机选择1至m对基因值不相等的基因互换基因值。这样相对于固定基因对数的变异而言，能够更好地保证抗体群的多样性。

2.4 记忆库更新、接种疫苗和免疫克隆

在首次循环中，把可行解中抗体亲和度最大的前b个抗体及其对应的亲和度值分别赋值给抗体记忆库与亲和度记忆库。之后在每次循环完成时，将可行解中各抗体的亲和度值与亲和度记忆库中的亲和度值进行比较，若可行解的亲和度更高，让它取代记忆库中比它低的亲和度，并用与之对应的抗体取代抗体记忆库中的抗体，这样可保证记忆库中的抗体总是亲和度最高的前b个抗体。

将抗体记忆库中的抗体作为疫苗，对变异后的不可行解中的一部分进行疫苗接种，使每次循环开始前产生的抗体群都朝着亲和度更高的方向发展，使程序能更快地向全局最优解收敛。

为了促进有用抗体的繁殖和抑制无用抗体的过度生成，程序每迭代一定次数后对可行解抗体进行一次克隆操作。具体的方法是将可行解抗体的期望繁殖率进行排序，弃掉排在后面的抗体，把前面的抗体进行克隆。这样能保证抗体的多样性，而且因为期望繁殖率高的抗体得到更多的繁殖，保留了更多有用基因，所以能加快程序向全局最优解收敛。

2.5 算法步骤

配电网重构的矢量距浓度免疫算法步骤如下：

步骤1生成规模为N0的初始抗体种群；

步骤2由基于最小生成树原理的网络全连通判定方法进行不可行解的判定；

步骤3利用前推回代法对可行解抗体进行配电网潮流计算，并算出相应抗体的亲和度、矢量矩、浓度、选择概率；

步骤4将可行解抗体的亲和度与记忆库中的亲和度进行比较，取代亲和度比之低的记忆库亲和度，并用与之对应的抗体取代抗体记忆库中的抗体；

步骤5根据可行解抗体的选择概率对它进行自适应变异，不可行解抗体进行分组全频变异；

步骤6将抗体记忆库中的抗体作为疫苗随机接种在变异后的新抗体群中；

步骤7步骤2～步骤6每迭代4次后，求出最后生成的可行解抗体的期望繁殖率，然后根据期望繁殖率对这些抗体进行克隆操作；

步骤8判断进化代数T是否到达设定值Ngen，若是，输出记忆库中的抗体和它们相对应的亲和度，并停止计算，否则置T=T+1，转步骤2。

3 算例分析

图1为某一实际配电网[6]，该网络具有4条馈线、69个节点、11个联络开关，基准电压为11 kV，图中实线代表分段开关，虚线代表联络开关。

图1 69节点系统

抗体长度取为76，抗体记忆库和抗体亲和度记忆库规模为20，种群规模为200，种群进化代数为500。表1为没有浓度控制的免疫算法IA(immune algorithm)和矢量距浓度免疫算法(VDIA)的结果。表2为信息熵浓度免疫算法IEIA(information entropy based immune algorithm)、欧氏距离浓度免疫算法EDIA(euclidean distance based immune algorithm)和矢量距浓度免疫算法(VDIA)的结果。表1和表2所得结果皆是在MATLAB2008中编程计算所得。

从表1可知，没有浓度控制的免疫算法可能会陷入局部最优解，而矢量距浓度免疫算法能收敛到全局最优。通过配电网重构，网损也降低不少，重构前系统网损为280.6 kW，由没有浓度控制的免疫算法得到的最优网损为247.4 kW，而矢量距浓度免疫算法得到的最优网损为246.4 kW；最低节点电压也从重构前的0.905分别上升到0.932和0.936。

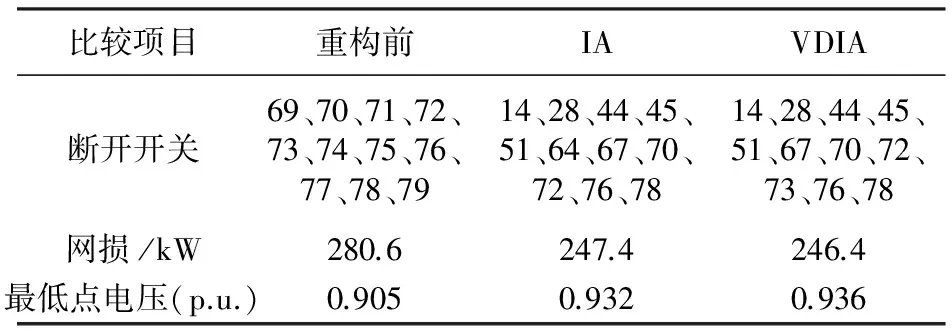
表1 配电网重构结果

表2 配电网重构的结果比较

从表2可知采用信息熵浓度免疫算法、欧氏距离浓度免疫算法和矢量距浓度免疫算法都能得到全局最优解，但是信息熵浓度免疫算法最快要792 s才能得到全局最优解，欧氏距离浓度免疫算法最快需810 s得到全局最优解，而矢量距浓度免疫算法最快只需要558 s就能得到全局最优解。3种方法在平均收敛时间上分别为993 s、1014 s和726 s。

4 结论

通过上述算例结果分析可知，基于矢量距浓度免疫算法能保证收敛到全局最优解，用矢量距来计算抗体的浓度、选择概率和期望繁殖率不仅计算简单，而且跟据选择概率进行变异操作和根据期望繁殖率进行克隆操作能很好地控制抗体浓度，保证抗体的多样性，从而加快了算法的收敛速度和保证了全局最优解的生成。

针对配电网的约束条件，略去了抗体的交叉操作过程，且在抗体变异时限定打开开关的数目，降低了不可行解的比例；通过免疫记忆机制，保留亲和度最低的可行解，加快了算法的收敛速度；抗体的变异概率采用了根据抗体选择概率而定的动态概率，在保证较优抗体的同时也不会降低抗体种群的多样性；对不可行解所对应的抗体采取注射疫苗的操作，增加了抗体种群中表现较优的基因数，提高了算法的收敛速度。

[1] Roytelman I，Melnik V，Lee S S H，etal．Multi-objective feeder reconfiguration by distribution management system[J]．IEEE Trans on Power Systems，1996，11(2)：661-667．

[2] 张栋，张刘春，傅正财(Zhang Dong，Zhang Liuchun，Fu Zhengcai)．配电网络重构的快速支路交换算法(A quick branch-exchange algorithm for reconfigureation of distribution networks)[J]．电网技术(Power System Technology)，2005，29(9)：82-85．

[3] 吴本悦，赵登福，刘 云,等(Wu Benyue，Zhao Dengfu，Liu Yun，etal)．一种新的配电网络重构最优流模式算法(An improved optimal flow pattern algorithm for distribution network reconfiguration)[J]．西安交通大学学报(Journal of Xi'an Jiaotong University)，1999，33(4)：22-24．

[4] Kim Hoyong，Ko Yunseok，Jung Kyung-Hee． Artificial neural-network based feeder reconfiguration for loss reduction in distribution systems [J]．IEEE Trans on Power Delivery，1993，8(3)：1356-1366．

[5] 姚李孝,任艳楠,费健安(Yao Lixiao, Ren Yannan, Fei Jianan). 基于蚁群算法的配电网网络重构(Ant colony system algorithm for distribution network reconfiguration)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(6)：35-39.

[6] 田佳(Tian Jia)．基于改进蚁群算法的配电网多目标重构问题研究 (Research of Multi-objective Reconfiguration of Distribution Network Based on Improved Ant Colony System Algorithm)[D]．保定：华北电力大学电气与电子工程学院(Baoding：School of Electrical and Electronic Engineering of North China Electric Power University)，2008．

[7] 靳晓凌，赵建国(Jin Xiaoling，Zhao Jianguo)．基于改进二进制粒子群优化算法的负荷均衡化配电网重构(Distribution network reconfiguration for load balancing based on improved binary particle swarm optimization)[J]．电网技术(Power System Technology)，2005，29(23)：40-43．

[8] 罗绮,吕林(Luo Qi, Lü Lin). 一种新的混合优化算法求解配电网重构(A new hybrid optimal algorithm to solve distribution network reconfiguration)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2009,21(1):89-92.

[9] 刘莉，陈学允(Liu Li，Chen Xueyun)．基于模糊遗传算法的配电网络重构(Reconfiguration of distribution networks based on fuzzy genetic algorithms)[J]．中国电机工程学报(Proceedings of the CSEE)，2000，20(2)：66-69．

[10]张利民,马 强,李振坤,等(Zhang Limin, Ma Qiang, Li Zhenkun,etal).基于禁忌克隆遗传算法的配电网故障恢复重构(Service restoration reconfiguration in distribution network based on tabu clonal genetic algorithm)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2010,22(1):60-64.

[11]蒙文川，邱家驹(Meng Wenchuan， Qiu Jiaju)．基于免疫算法的配电网重构(An artificial immune algorithm to distribution network reconfiguration)[J]．中国电机工程学报(Proceedings of the CSEE)，2006，26(17)：25-29．

[12]Belkacemi Rabie， Feliachi Ali． Multi-agent design for power distribution system reconfiguration based on the artificial immune system algorithm[C]∥IEEE International Symposium on Circuits and Systems.Paris, France: 2010.

[13]周愈鹏，相中华，叶高生,等(Zhou Yupeng ，Xiang Zhonghua ， Ye Gaosheng,etal)．基于免疫优势算法的配电网重构(An artificial immunodominance algorithm to distribution network reconfiguration)[J]．电气开关(Electric Switchgear)，2009，47(1)：16-19．

[14]孙梦娴，陈小平(Sun Mengxian，Chen Xiaoping)． 矢量矩浓度的免疫算法在函数优化中的应用(An immune algorithm based on the vector distance applied to function optimization)[J]．苏州大学学报:工科版(Journal of Suzhou University:Engineering Science Edition)，2010，30(3)：56-60．

[15]毕鹏翔，刘健，刘春新,等(Bi Pengxiang，Liu Jian，Liu Chunxin，etal)．配电网络重构的改进遗传算法(A refined genetic algorithm for power distribution network reconfiguration)[J]．电力系统自动化(Automation of Electric Power Systems)，2002，26(2)：57-61．

李 樊(1987-)，男，硕士研究生，研究方向为电力系统稳定与控制。Email:573286191@qq.com

刘天琪(1962-)，女，博士，教授，博士生导师，研究方向为电力系统分析计算与稳定控制、高压直流输电、调度自动化。Email:tqliu@sohu.com

李兴源(1945-)，男，教授，博士生导师，中国电机工程学会理事，IEEE高级会员，主要从事电力系统稳定与控制、高压直流输电、分布式发电等研究。Email:x.y.li@163.com

ApplicationofVectorDistanceAntibodyDensityBasedImmuneAlgorithminDistributionNetworkReconfiguration

LI Fan， LIU Tian-qi， LI Xing-yuan， JIANG Dong-lin

(School of Electrical Information, Sichuan University, Chengdu 610065, China)

A new immune algorithm based on vector distance density is proposed to solve the problems that immune algorithm often faces in network reconfiguration, such as slow convergence and easy convergence to local optimal solution. The vector distance is decided by the antibody's affinity, and the antibody density, select probability and expected reproductive rate of antibody obtained. The antibody mutation rate was adaptive according to the selection probability, and the diversity of antibody and global optimal solution is ensured by the cloning operation which was based on expected reproductive rate. Finally, the combination of vaccination and immune memory mechanisms can promote the formation of the global optimal solution. The example verifies the algorithm that can enhance convergence speed and ensure the global optimal solution' generation.

vector distance based immune algorithm (VDIA)； distribution network reconfiguration； mutation； cloning； vaccination； immune memory

TM72

A

1003-8930(2012)01-0079-05

2010-12-20；

2011-03-03

国家科技支撑计划项目(2008BAA13B01)