基于模拟植物生长算法的电力系统ATC计算

张瑞阳， 冯怀玉， 李国庆， 姜 涛， 徐文卿

(1.中国南方电网电力调度通信中心， 广州 510623； 2.西安供电局， 西安 710032；3.东北电力大学电气工程学院， 吉林 132012)

基于模拟植物生长算法的电力系统ATC计算

张瑞阳1， 冯怀玉2， 李国庆3， 姜 涛3， 徐文卿3

(1.中国南方电网电力调度通信中心， 广州 510623； 2.西安供电局， 西安 710032；3.东北电力大学电气工程学院， 吉林 132012)

提出将模拟植物生长算法PGSA(plant growth simulation algorithm)应用于可用输电能力ATC(available transfer capability)计算。该方法结合电力系统ATC求解特点，将不等式约束转化为PGSA算法可行域，计算等式约束的可能解；引入步长自适应调整机制，动态调整寻优步长。由于将ATC目标和约束分开处理，采用兼顾方向性和随机性的搜索机制，无需引入罚函数处理约束条件，避免因参数不确定性和寻优方向无引导性而陷入局部最优。IEEE-30节点系统仿真结果验证了所提方法的有效性。

可用输电能力； 模拟植物生长算法； 全局优化； 自适应变步长

可用输电能力ATC(available transfer capability)是指在现有的输电合同基础上，实际物理输电网络中剩余的、可用于商业使用的输电容量[1]。在电力市场环境下，可用输电能力在维持系统安全运行、处理输电阻塞、引导市场交易等方面具有重要意义[2，3]。如何准确快速地确定系统ATC值近年已成为研究者关注的焦点[4～7]。ATC的计算是一项十分复杂的工作，它既要考虑多种因素影响，如系统运行状态、电网结构等；还应考虑系统多种约束条件的限制，如节点电压约束、过负荷约束等静态安全性约束、暂态稳定约束和动态稳定性约束[8～12]。从数学本质看，ATC是考虑了系统安全性约束下的优化问题[2，6～8]。目前，常用优化算法有：内点法[13，15]、Benders[14]、牛顿法[16]、区间线性规划[17]等经典优化算法以及遗传算法[18]、粒子群算法PSO(particle swarm optimization)[19]等现代智能算法。然而，经典算法要求ATC目标函数连续可微且采用单一搜索机制，很难跳出局部最优；智能算法需给出诸如罚函数、交叉率、变异率、初始染色体群等参数，而这些参数选取至今仍无确定的准则。模拟植物生长算法PGSA(plant growth simulation algorithm)是一种专门用于求解非线性规划问题的仿生类搜索算法[20]。该算法将目标函数和约束条件分开处理，不要求目标函数连续、可微，具有较强全局寻优能力，且不需引入诸如罚函数等参数来处理约束条件等优点，已应用于分布式电源规划[21]、机组检修[22]、无功优化[23]、配电网重构[24]、输电网规划[25]等领域。

本文将PGSA应用于电力系统的ATC计算中。建立常规静态完全约束的ATC优化模型，并针对ATC优化模型的特点将PGSA进行适当改进，使PGSA具有更强的全局搜索能力；最后，应用改进后的PGSA对ATC模型进行求解，并以标准算例的仿真加以验证。

1 ATC数学模型

ATC计算采用的目标函数是送电区域对外联络线的总传输功率与基态潮流之差的最大化，即

(1)

等式约束为系统潮流方程，即

(2)

式中：Pi、Qi分别为节点i注入的有功和无功功率；Vi、Vj分别为节点i、j的电压幅值；θij为节点i、j间的电压相位差；Gij、Bij为节点i、j间的支路电导和电纳。

不等式约束考虑系统发电机组出力约束，负荷容量约束，节点电压以及线路功率约束，即

(3)

式中：PG,i为第i台发电机的有功功率；QG,i为第i台发电机的无功功率；PL,j为负荷节点j的有功功率；QL,j为负荷节点j的无功功率；Vi为i节点的电压幅值；Pij为支路ij流过的有功功率；αG为所有发电机节点集合；αL为所有负荷节点集合；αN为系统所有节点集合；min、max分别表示变量下、上限。

2 改进模拟植物生长算法

2.1 模拟植物生长算法(PGSA)

PGSA模拟植物生长机制，将整数规划可行域当作植物生长环境，将全局最优解当作光源，模拟植物向光性机理(形态素)建立了枝叶在不同光线强度下(吸引域)向光源(全局最优解)快速生长的动力机制[20]。PGSA将可行域初始解定义为树根，根据可行域范围确定树干长度，从树根出发利用树干和树枝建立跨越整数规划可行域的拓扑结构，生长点模拟植物系统的位置点，然后利用植物向光性特点，保证在众多生长点中树枝向最优解方向快速运动。由植物生长过程的生物学结论可知：植物有一个以上的节时，形态素浓度高的生长点能优先生长；生长点从其环境中接受位置信息，依据这种信息确定生长点的形态素浓度；新生长点产生后，形态素浓度将根据新系统所在环境改变，重新分配。

基于上述思想，文献[21]建立了模拟植物向光性的概率生长模型：植物从根部所在点S0开始生长出的茎秆长度为M，上面有K个初始生长点SM=(SM1，SM2，…，SMK)，每个生长点的形态素浓度为PM=(PM1,PM2,…,PMK)；设树枝的单位长度为m(mlt;M)上面有q个生长点Sm=(Sm1,Sm2,…,Smq)，其形态素浓度为Pm=(Pm1,Pm2,…,Pmq)。树干及树枝上各生长点形态素浓度值为

(4)

式中：x0为初始可行解即树根；f(·)为所在生长点的背光函数值(即目标函数值)，其值越小则对应的生长点光照条件越好。

式(4)物理意义为：各生长点形态素浓度P由各点与树根的相对位置以及该位置环境信息(目标函数值)确定。该式真实刻画了生长点形态素浓度与环境条件之间的对应关系，这与真实植物细胞的形态素浓度生成机理相一致。由式(4)可知

(5)

即所有的形态素浓度构成如图1所示的状态空间，该状态空间可描述为：在区间[0，1]由计算机产生随机数η，η在[0，1]闭区间所对应的生长点作为下一个循环的新基点并优先长出新枝n，新枝n在长成后，树干M和树枝m上的k和l生长点的形态素浓度都发生变化，此过程反复进行，直到没有新枝产生，此时的树枝点即为优化问题的最优解。

图1 形态素浓度状态空间

从数学优化角度可知，茎秆和树枝表示控制变量的可行域；生长点表示控制变量的可能解；根部表示控制变量的初始值；f(·)为目标函数值。

2.2 模拟植物生长算法的改进

(1)结合PGSA本身对形态素浓度的生物学定义，本文将ATC的不等式约束构成一个植物生长的可行域，在此可行域内各生长点形态素浓度由式(4)确定，而不属于该可行域的生长点形态素浓度全部为0，由此保证植物只在可行域内生长，即寻优过程都在ATC的不等式约束范围内进行。

(2)PGSA是一种用于求解整数规划问题的仿生类概率搜索算法，即寻优步长固定为整数，在ATC求解过程中会出现迭代寻优精度不高和迭代次数过多等问题。因此本文引入自适应步长机制，在寻优过程中，当循环次数是1 或循环次数是树干上的生长点个数K的整数倍时, 步长取茎秆长度M，其余循环步长均取树枝长度m。当迭代精度满足一定误差后，若原始步长为茎秆长度M，则新步长为茎秆长度M除以K；若原步长为树枝长度m，则新步长为树枝长度m除以q，以动态调整寻优步长，提高寻优精度和收敛速度，这样使步长的选取较为灵活，可保持生长点集内生长点的多样性，避免陷入局部最优解, 提高全局寻优能力。

3 基于PGSA的ATC求解

本文中，ATC计算采用的目标函数是送电区域对外联络线的总传输功率与基态潮流之差的最大化，控制变量是送电区域发电机有功功率和受电区域负荷有功功率。采用PGSA计算ATC时，约束条件的处理方法如下。

等式约束，通过计算每个生长点的潮流，满足约束条件的生长点保留在生长点集合中，不满足的直接舍弃；不等式约束，通过限定树干及树枝的长度来实现。此外引入自适应步长，根据迭代次数自动调整生长步长，加速算法收敛。应用PGSA求解ATC的具体流程如图2所示。

图2 PGSA算法计算ATC流程

4 算例分析

为验证本文所构建ATC模型及所采用算法的正确性和有效性，采用IEEE-30节点系统进行仿真验证。IEEE-30节点系统划分为3个区域，具体分区如图3所示，系统详细参数见文献[9]。

4.1 结果分析

采用文献[19]中的改进粒子群IPSO(improved particle swarm optimization)算法和PGSA对不同区域间的ATC进行计算，计算结果如表1所示。采用PGSA算法计算得到的2-3区，3-2区ATC值大于IPSO的计算结果。这是因为PGSA既能够克服经典优化算法要求目标函数和约束条件连续、可微以及单一的搜索机制，又避免了IPSO算法需引入罚函数及初始参数的选取问题。

图3 IEEE-30节点系统

表1 PGSA与IPSO计算结果比较

为更详细阐述PGSA算法是如何求解ATC问题，本文以2-3区PGSA计算结果为例，说明如何调整送电区发电机功率的输送以及受电区节点负荷功率的增量，使两区域ATC达到最大，计算结果见表2，其中下标表示节点号。

表2 2-3区各控制变量的值

2区中有两台发电机，假设其他区域发电机按基态潮流，在运算中以2区其中一台发电机为平衡机(本例中为23)，另外一台的有功输出为PGSA算法中一个控制变量(共1个变量)；3区有7个负荷节点，假设其他区域负荷节点功率按照基态潮流输出, 3区所有负荷节点的有功和无功分量作为PGSA算法的控制变量(共14个变量)，则控制变量一共15个，相当于植物要在15维空间寻优(即K=15，q=14)。目标函数相当于形态素浓度，各个生长点通过根据形态素浓度选择生长步长和方向。通过寻优后，本文列出一次寻优后各变量的值，如表2所示。

4.2 收敛性分析

限于篇幅，表3列出了采用IPSO和PGSA两种算法下 2-3区的ATC计算结果，其结果与迭代次数对比如表3 所示，收敛曲线对比如图4所示。

从表3中的ATC值和迭代次数来比较，可以看出PGSA算法计算ATC值明显大于IPSO，同时该算法能更快收敛到最优解；样本方差小，说明该算法的稳定性更强，验证了该算法的有效性。

表3 PGSA、IPSO 计算2-3区ATC结果和迭代次数比较

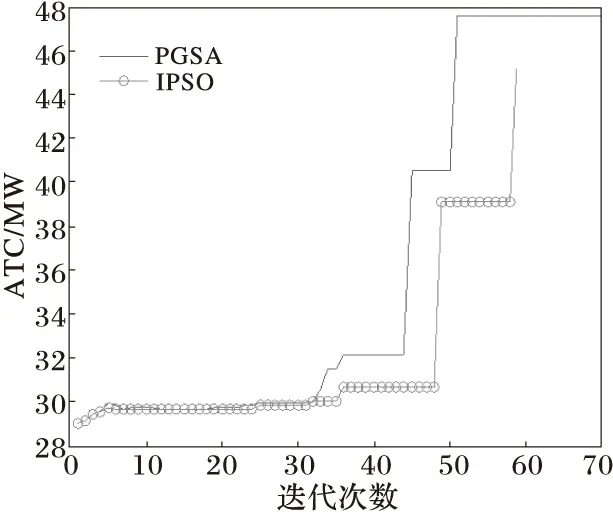
图4 基于PGSA和IPSO的收敛特性曲线

对比图4中IPSO和PGSA的收敛曲线可知，①两种算法收敛曲线初始点一致，而PGSA爬坡速度较IPSO更快，通过较少迭代次数便可迅速达到最优解；②目标函数在35 MW附近时出现了暂时的停顿，这说明植物生长时在这附近已经达到了局部最优位置，但PGSA较IPSO具有更强的全局搜索能力，故能够更快地跳出了这一局部最优解；③在43 MW附近的短暂停顿则是由于步长的选取不当，导致植物暂停生长，由于自适应步长机制的引入，弥补了这种不足，故很快达到了更优的位置。避免了大量时间浪费在寻优过程中，保证算法能够很快跳出局部最优，快速向全局最优解方向搜索，提高了ATC计算速度。

5 结语

本文将模拟植物生长算法(PGSA)应用于电力系统的ATC计算中。针对ATC求解中存在等式约束和不等式约束的特点，对PGSA适当改进，并引入自适应变步长，动态调整计算过程中的寻优步长，提高了PGSA寻优精度和ATC计算准确性；将ATC的目标函数和约束条件分开处理，无需引入罚函数等参数处理约束条件，避免已有仿生类算法由于一些参数难以确定而陷入局部最优，加快了收敛速度；PGSA只利用ATC的目标函数取值信息，对ATC具体特点无过多要求，全局寻优能力较强，对初值不敏感，解的稳定性好。

[1] North American Electric Reliability Council ．Available transfer capability definitions and determination[R]．USA：North American Electric Reliability Council ，1996．

[2] 李国庆，王成山，余贻鑫(Li Guoqing，Wang Chengshan，Yu Yixin)．大型互联电力系统区域间功率交换能力研究综述(A survey on transmission transfer capability of interconnected electric power systems)[J]．中国电机工程学报(Proceedings of the CSEE)，2001，21(4)：20-25．

[3] 王成山，王兴刚，魏炜(Wang Chengshan，Wang Xinggang，Wei Wei)． (Study on available transfer capability of power systems)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA) ，2005,17(5)：42-49．

[4] 李国庆，王成山，余贻鑫(Li Guoqing，Wang Chengshan，Yu Yixin)．考虑ULTC和SVC等影响的功率交换能力的分析与计算(Analysis and calculation of transmission transfer capability considering some influencing factor)[J]．电网技术(Power System Technology)，2004，28(2)：17-22．

[5] 孙欣，夏清(Sun Xin , Xia Qing)．基于交易空间的可用传输容量计算方法(Calculation of available transfer capability in transaction space)[J]．电力系统自动化(Automation of Electric Power Systems)，2009，33(10)：11-15．

[6] 汪峰，白小民(Wang Feng，Bai Xiaomin)．基于最优潮流方法的传输容量计算研究(OPF based transfer capability calculation) [J]．中国电机工程学报(Proceedings of the CSEE)，2002， 22(11)：35-40．

[7] 李生虎，丁明，吴红斌，等(Li Shenghu，Ding Ming，Wu Hongbin，et al)．基于安全性的互联电网间最大输电容量的研究(Research of total transfer capability among power systems considering security)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2003,15(5)：1-4,38.

[8] 潘雄，徐国禹(Pan Xiong，Xu Guoyu)．基于最优潮流并计及静态电压稳定性约束的区域间可用输电能力计算(OPF based ATC calculation with static voltage stability constraints)[J]．中国电机工程学报(Proceedings of the CSEE)，2004，24(12)：86-91．

[9] 李国庆，沈杰，申艳杰(Li Guoqing，Shen Jie，Shen Yanjie)．考虑暂态稳定约束的可用功率交换能力计算的研究(Study on calculation of available transfer capability considering transient stability constraints) [J]．电网技术(Power System Technology)，2004，28(15)：67-71．

[10]李国庆，郑浩野(Li Guoqing，Zheng Haoye)．一种考虑暂态稳定约束的可用输电能力计算的新方法(A novel algorithm for available transfer capability considering transient stability constraints)[J]．中国电机工程学报(Proceedings of the CSEE)，2005，25 (15)：20-25．

[11]方鸽飞，黄晓烁，梁成红(Fang Gefei, Huang Xiaoshuo, Liang Chenghong)．考虑电压稳定的预想事故下最大输电能力分析(TTC analysis in contingency based on voltage stability)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA) ，2003,15(5)：5-8,27.

[12]房大中，吴明波，李传栋，等(Fang Dazhong，Wu Mingbo，Li Chuandong，etal)．热稳定约束下断面输电极限分析方法(Analysis method of transfer capability of transmission interfaces under thermal stability constraints)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA) ，2007,19(4)：111-115．

[13]王良缘，吴政球，傅海燕，等(Wang Liangyuan，Wu Zhengqiu，Fu Haiyan，etal)．电力市场中基于内点法的含暂态稳定约束的最大可用输电能力计算(Calculation of available transfer capability(ATC) taking into account transient stability constraints based on interior-point solution in electricity market)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2004,16(1)：28-33,46.

[14]默哈莫德·夏班，刘皓明，倪以信，等(Mohamed Shaaban，Liu Haoming ，Ni Yixin，etal)． 静态安全约束下基于Benders分解算法的可用传输容量计算(ATC calculation with static security constrains using Benders decomposition)[J]．中国电机工程学报(Proceedings of the CSEE)， 2003，23 (8)：7-11．

[15]陈妍，黄民翔(Chen Yan, Huang Minxiang)．基于信赖域内点法的静态ATC计算(Static ATC calculation based on a trust region interior-point method)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA) ，2005,17(5)：71-74．

[16]李国庆，李雪峰，沈杰，等(Li Guoqing，Li Xuefeng，Shen Jie，etal)．牛顿法和内点罚函数法相结合的概率可用功率交换能力计算(A probability ATC computation by a combination of Newton's method with SUMT interior point method)[J]．中国电机工程学报(Proceedings of the CSEE)，2003,23(8)：17-22．

[17]孙欣，方陈，夏清(Sun Xin，Fang Chen，Xia Qing)．基于区间规划的可用传输容量计算方法(Available transfer capability calculation based on interval programming)[J]．电力系统自动化(Automation of Electric Power Systems)，2011，35(3)：15-20．

[18]Mozafari Babak， Ranjbar Ali Mohammad，Shirani Ali Reza，etal．A comprehensive method for available transfer capability calculation in a deregulated power system[C]∥IEEE International Conference on Electric Utility Deregulation Restructuring and Power Technologies.Hong Kong，China: 2004．

[19]李国庆，陈厚合(Li Guoqing，Chen Houhe)．改进粒子群优化算法的概率可用输电能力研究(Study of probabilistic available transfer capability by improved particle swarm optimization)[J]．中国电机工程学报(Proceedings of the CSEE)，2006，26(24)：18-23．

[20]李彤，王春峰，王文波，等(Li Tong，Wang Chunfeng，Wang Wenbo，etal)．求解整数规划的一种仿生类全局优化算法——模拟植物生长算法(A global optimization bionics algorithm for solving integer programming-plant growth simulation algorithm)[J]．系统工程理论与实践(System Engineering Theory and Practice)，2005，25 (1)：76-85．

[21]张节潭，程浩忠，姚良忠，等(Zhang Jietan，Cheng Haozhong，Yao Liangzhong，et al)．分布式风电源选址定容规划研究(Study on sitting and sizing of distributed wind generation)[J].中国电机工程学报(Proceedings of the CSEE)，2009，29(16)：1-7．

[22]王淳，程浩忠，谭永香，等(Wang Chun，Cheng Haozhong，Tan Yongxiang，etal)．发电机组检修计划的模拟植物生长算法(Plant growth simulation algorithm for generator maintenance scheduling)[J]．电工技术学报(Transactions of China Electrotechnical Society)，2008，23(9)：105-110．

[23]杨丽徙，丁荣刚，王西训(Yang Lixi，Ding Ronggang，Wang Xixun)．工业企业配电网无功电源的两阶段优化规划(Two-phase optimization planning of reactive power supply for factory power grid)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA) ，2010,22(2)：32-36．

[24]王淳，程浩忠(Wang Chun，Cheng Haozhong).基于模拟植物生长算法的配电网重构(Reconfiguration of distribution network based on plant growth simulation algorithm)[J]．中国电机工程学报(Proceedings of the CSEE)，2007，27(19)：50-55．

[25]王淳，程浩忠(Wang Chun，Cheng Haozhong).模拟植物生长算法及其在输电网规划中的应用(A plant growth simulation algorithm and its application in power transmission network planning) [J]．电力系统自动化(Automation of Electric Power Systems)，2007,31(7):24-28．

张瑞阳(1979-)，男，工程师，研究方向为电力系统运行与控制。Email:ZhangRY@CSG.cn

冯怀玉(1986-)，女，硕士，研究方向为电力系统安全性和稳定性分析。Email:fenghuaiyu203@163.com

李国庆(1963-)，男，博士，教授，博士生导师，研究方向为电力系统安全性和稳定性分析、控制与决策、配电系统自动化。Email:lgq@mail.nedu.edu.cn

AvailableTransferCapabilityComputationUsingPlantGrowthSimulationAlgorithm

ZHANG Rui-yang1， FENG Huai-yu2， LI Guo-qing3， JIANG Tao3， XU Wen-qing3

(1.CSG Power Dispatching and Communication Center, Guangzhou 510623, China;2.Xi'an Power Supply Bureau, Xi'an 710032, China;3.Northeast China Dianli University, School of Electrical Engineering, Jilin 132012, China)

A method using plant growth simulation algorithm (PGSA) for available transfer capability (ATC) calculation was proposed in the paper. Combining solution features of ATC, inequality constraints are converted to a feasible region of PGSA to calculate the possible solution of equality constraints, and step-size adaptive adjustment mechanism is used to adjust step-size dynamically during the optimal proceeding. As the objective function and constraints of ATC are handled by PGSA separately and adopting directional and random search mechanism, the proposed method doesn't need penalty functions to handle constraints, and avoids falling into local optimal which may appear in conventional optimal algorithms. IEEE-30 bus test system simulation results verify the effectiveness and accuracy of the method.

available transfer capability(ATC)； plant growth simulation algorithm(PGSA)； global optimization； adaptive variable-step size

TM711； TM721.2

A

1003-8930(2012)01-0037-06

2011-10-11；

2011-11-09

国家自然科学基金资助项目(50977009)