考虑异步电动机的动态电压稳定特征值指标

井艳清， 李兴源， 吴华坚， 顾 威， 郭晓鸣， 陈 虎， 周 健

(1.四川大学电气信息学院， 成都 610065； 2.华能小湾水电厂， 南涧 675702)

考虑异步电动机的动态电压稳定特征值指标

井艳清1， 李兴源1， 吴华坚1， 顾 威1， 郭晓鸣1， 陈 虎1， 周 健2

(1.四川大学电气信息学院， 成都 610065； 2.华能小湾水电厂， 南涧 675702)

为更加精确、快速地判断系统动态电压稳定性，提出了系统动态电压稳定的特征值指标IDVSE(dynamic voltage stability eigenvalue index)，并计及异步电动机负荷三阶机电暂态模型，对异步电动机负荷进行暂态等效和特征值分析，进而判断系统动态电压稳定性。该指标克服了动态电压稳定指标的不精确性和计算量大等问题。BPA软件对IEEE30系统的时域仿真结果验证了该指标的有效性和准确性。

动态电压稳定； 异步电动机； 特征值； 指标； 时域仿真

近年来实际电力系统的电压失稳事故时有发生，引起人们对电压稳定研究的高度重视。研究表明，系统中各母线电压动态行为主要取决于系统中负荷的动态特性和各种电压调节装置的动作特性。异步电动机是最主要的动态负荷，也是引起系统发生电压失稳的重要原因[1，2]。因此，电压稳定分析中计及异步电动机负荷，能更真实地反映电力系统用电负荷的实际情况，得出准确的分析结果[3]。

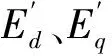
1 异步电动机模型

异步电动机负荷采用三阶机电暂态模型，其稳态等效电路如图1所示[7]，其暂态等效电路如图2所示，其转子电压方程[8]为

(1)

(2)

定子电流方程为

(3)

(4)

转子运动方程[9，10]为

(5)

(6)

(7)

式中：ωt=1-S，S为转子转差；Tj为发电机组的惯性时间常数；Te为电动机电磁转矩；Tm为电动机机械转矩；Ud和Uq分别为定子电压U的直、交轴分量；a、b、c为机械转矩系数，其计算式为

(8)

异步电动机动态电势计算公式为

(9)

(10)

图1 异步电动机稳态等效电路

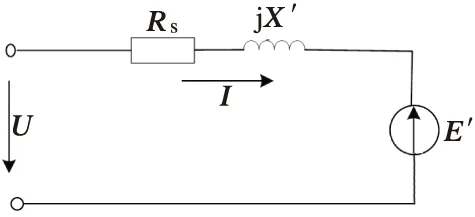
图2 异步电动机暂态等效电路

2 动态电压稳定特征值指标

文献[11]认为只要系统中有一个感应电动机负荷被判为失稳，就认为系统电压失稳；只有系统中所有感应电动机负荷都被判为稳定，才能判定系统电压稳定。文献[12]也认为只要负荷失稳，则系统电压失稳。因此，本文通过研究异步电动机负荷的稳定性来判断电力系统的电压稳定性，只要异步电动机负荷动态失稳，则判断系统动态电压失稳。

对式(1)、式(2)、式(5)进行线性化就可得到异步电动机动态方程的系统矩阵[11～14]为

(11)

异步电动机的动态过程由3个状态变量来描述，因此有3个特征值与之相对应，包括1对共轭复特征值和1个实特征值。其中1对共轭特征值与异步电动机转子绕组电路的电磁暂态特性密切相关，称为转子特征值；实特征值与异步电动机转子转差密切相关，称为转差特征值。令系统状态矩阵A中定子电压为故障切除时刻异步电动机定子电压，转差为故障切除时刻转差Sc，则有

(12)

设系统状态矩阵A′转差特征值为λ，定义IDVSE为系统动态电压稳定特征值指标，有

IDVSE=λ

(13)

由系统矩阵特征值性质可知，当IDVSElt;0时，该负荷节点动态电压稳定；当IDVSE=0时，该负荷节点临界动态电压稳定；当IDVSEgt;0时，该负荷节点动态电压失稳。

定义系统状态矩阵A′的零特征值(λ=0)对应的故障切除时刻端电压Uc为动态稳定临界电压Uc(λ=0)。当Ucgt;Uc(λ=0)时，该负荷节点动态电压稳定；当Uc=Uc(λ=0)时，该负荷节点临界动态电压稳定；当Uclt;Uc(λ=0)时，该负荷节点动态电压失稳。

3 IEEE30节点系统算例仿真分析

保持异步电动机负荷功率因数cosφ不变。本文通过对IEEE30节点系统进行分析计算，以验证所提出的动态电压稳定特征值指标IDVSE的正确性和有效性。IEEE30节点系统中BUS4、BUS14、BUS29计及异步电动机负荷，本文选取母线BUS4和母线BUS29作为研究对象。计算步长为0.02 s，仿真时间为10 s，故障发生时刻为1.0 s。取系统容量基准SB=SN，异步电动机负荷参数值见表1。

表1 异步电动机负荷三阶机电暂态模型参数

3.1 故障方案一

母线BUS4为100%异步电动机负荷，将母线BUS4负荷功率增加到初始功率的2倍，其余负荷母线保持初始功率。母线BUS4和母线BUS6之间线路50%处发生三相短路故障，经过时域仿真分析，该系统动态电压稳定的极限切除时间为0.57 s。故障持续时间不同时，负荷母线BUS4的动态电压稳定分析结果见表2。

图3 不同故障持续时间BUS4的动态电压稳定特征值指标

图4 故障切除时间为1.56 s时BUS4的时域仿真曲线

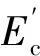
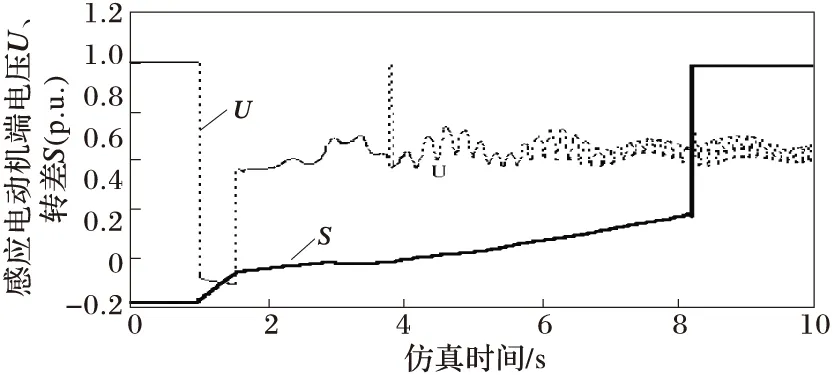
图5 故障切除时间为1.58 s时BUS4的时域仿真曲线

3.2 故障方案二

母线BUS29为50%异步电动机负荷和50%ZIP负荷，将母线BUS29负荷功率增加到初始功率的4倍，其余负荷母线保持初始功率。母线BUS29线路开关后发生三相短路故障，经过时域仿真分析，该系统动态电压稳定的极限切除时间为1.56 s。故障持续时间不同时，负荷母线BUS29的动态电压稳定分析结果见表3。

由表3数据可看出，时域仿真极限切除时间为1.56 s，本文指标极限切除时间也为1.56 s，可见本文指标的精确性。

取不同故障切除时刻(本文取2.48～2.66s)时域仿真数据，经过计算作图6，取故障切除时间分别为2.54 s、2.56 s的时域仿真曲线见图7和图8。由图6可看出极限切除时间为1.56 s，此时特征值指标为0，判定为动态电压失稳，时域仿真极限切除时间也为1.56 s；由图7看出转差并未达到1，转子并未堵转，由图8可看出转差在9.92 s达到1，转子堵转，系统电压失稳。

综看表2、表3、图3～图8，可见本文指标较简单并且准确度较高。

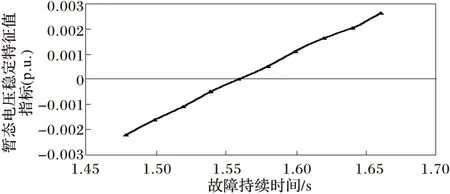
图6 不同故障持续时间BUS29的动态电压稳定特征值指标

表2 负荷母线BUS4不同故障切除时刻矩阵A′的特征值

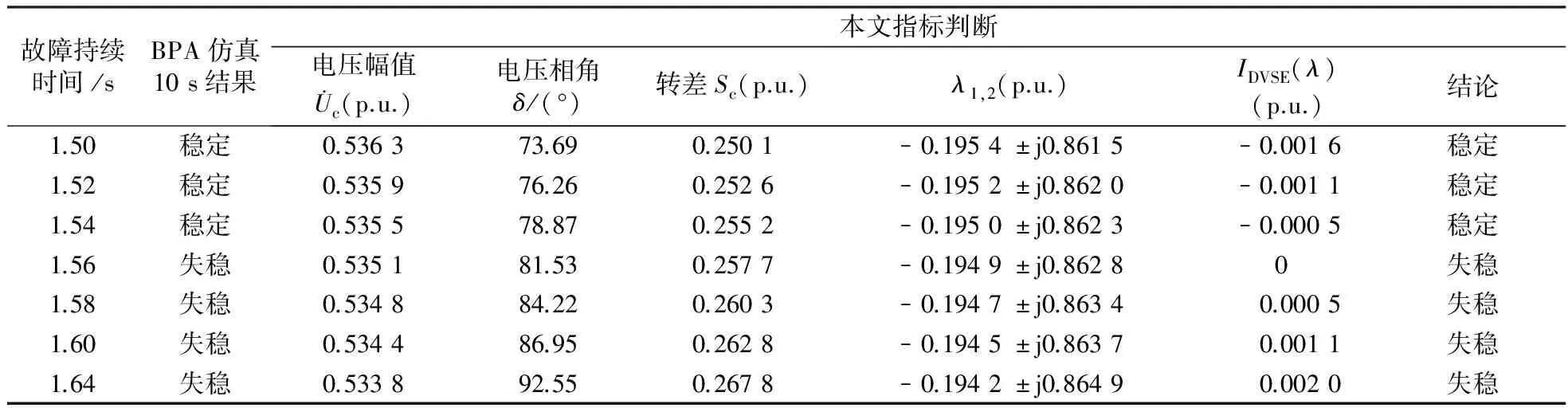
表3 负荷母线BUS29不同故障切除时刻矩阵A′的特征值

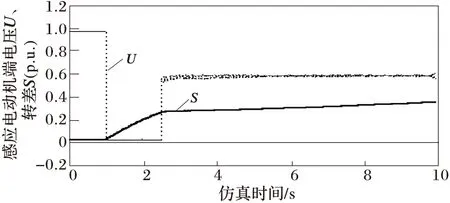
图7 故障切除时间为2.54 s时BUS29的时域仿真曲线

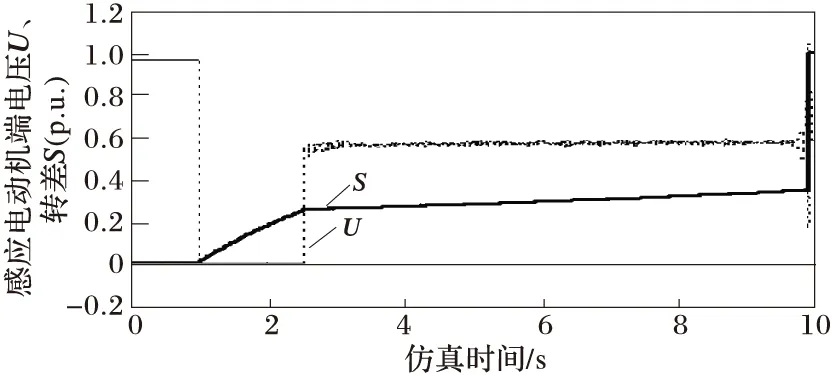
图8 故障切除时间为2.56s时BUS29的时域仿真曲线

4 结论

本文在考虑动态异步电动机负荷的基础上，将特征值用于动态电压稳定分析，并改进了异步电动机动态方程线性化后得到的系统状态矩阵A，提出了动态电压稳定特征值指标IDVSE。BPA时域仿真分析结果表明，IDVSE指标较以往的电压稳定指标更能准确的判定系统的动态电压稳定性，得出较准确的分析结果。且该指标较简单，计算量较小，更方便实际工程应用。

[1] 李鹏,余贻鑫,贾宏杰,等(Li Peng,Yu Yixin,Jia Hongjie,etal). 小扰动电压稳定分析的P-H模型及振荡阻尼因子(P-H model for small signal voltage stability analysis and voltage oscillation damping factor) [J].中国电机工程学报(Proceedings of the CSEE),2003,23(12):19-22.

[2] 李欣然,贺仁睦,周文,等(Li Xinran,He Renmu,Zhou Wen,etal).综合负荷的广义感应电动机模型及其描述能力(The generalized induction motor and its description ability for synthetic loads for electric power system) [J].华北电力大学学报(Journal of North China Electric Power University),1999,26(1):18-24.

[3] 孙华东,周孝信(Sun Huadong,Zhou Xiaoxin).计及感应电动机负荷的电力系统在线电压稳定指标(An on-line voltage stability index of power system considering induction motor loads) [J].中国电机工程学报(Proceedings of the CSEE)，2006,26(6):1-7.

[4] 马林,廖培金,彭书涛(Ma Lin，Liao Peijin, Peng Shutao). 小干扰稳定中特征值对运行参数的灵敏度(Eigenvalue sensitivity with respect to operating parameters in small signal stability analysis) [J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(4):31-35.

[5] 张艳萍,张建华(Zhang Yanping, Zhang Jianhua).小扰动特征分析法在电压稳定分析中的应用(Application of eigenvalue analysis in small disturbance voltage stability) [J].华北电力大学学报(Journal of North China Electric Power University),2008,35(3):17-23.

[6] Ajjarapu V, Lee B. Bibliography on voltage stability[J].IEEE Trans on Power Systems,1998,13(1):115-125.

[7] 周双喜,朱凌志,郭锡玖,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社,2004.

[8] 汤涌,侯俊贤,刘文焯(Tang Yong,Hou Junxian,Liu Wenzhuo).电力系统数字仿真负荷模型中配电网络及无功补偿与感应电动机的模拟(The modeling of distribution network and var compensator and induction motor in the load model for power system digital simulation) [J].中国电机工程学报(Proceedings of the CSEE),2005,25(3):8-12.

[9] 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京：清华大学出版社,2002.

[10]Hundur P.电力系统稳定与控制[M].北京:中国电力出版社,2001.

[11]徐泰山,薛禹胜,韩祯祥(Xu Taishan,Xue Yusheng,Han Zhenxiang).感应电动机暂态电压失稳的定量分析(Quantitative analysis for transient voltage instability caused by induction motors) [J].电力系统自动化(Automation of Electric Power Systems),1996,20(6)：12-15.

[12]孙华东(Sun Huadong).计及感应电动机负荷的电压稳定分析及其应用研究(Study on Voltage Stability Analysis and Its Application Considering Induction Motor Loads)[D].北京:中国电力科学研究院(Beijing: China Electric Power Research Institute)，2005.

[13]郭琼, 姚晓宁(Guo Qiong,Yao Xiaoning). 浅析电力系统负荷对电压稳定性的影响(Influence analysis of load on the power voltage stability)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(3):61-65.

[14]赵勇(Zhao Yong). 感应电动机负荷模型的静态特性分析(Analysis on static characteristics of induction motor models)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(2):86-92.

井艳清(1987-)，女，硕士研究生，研究方向为电力系统分析计算及稳定。Email:419188621@qq.com

李兴源(1945-)，男，教授，博士生导师，中国电机工程学会理事，IEEE 高级会员，主要从事电力系统稳定与控制等方面的研究工作。Email:x.y.li@163.com

吴华坚(1986-)，男，硕士研究生，主要从事电力系统稳定分析和控制及其高压直流输电系统的分析和研究工作。Email:moyan19861023@163.com

DynamicVoltageStabilityEigenvalueIndexConsideringAsynchronousMotors

JING Yan-qing1， LI Xing-yuan1， WU Hua-jian1， GU Wei1，GUO Xiao-ming1， CHEN Hu1， ZHOU Jian2

(1.School of Electrical and Information, Sichuan University, Chengdu 610065, China;2.Huaneng Lancang Riler Hydroponer Co.Ltd, Nanjian 675702, China)

In order to determine the system dynamic voltage stability more accurately and quickly,a system dynamic voltage stability index is proposed.Considering third-order transient model of asynchronous motor load and on the base of the transient equivalent of the asynchronous motor load, the eigenvalue of asynchronous motor load is analyzed in order to determine the system dynamic voltage stability. The index overcomes the shortages of the past indexes, such as imprecision and large computation. The time domain simulation results on IEEE30 system by using BPA verify the validity and accuracy of the index.

dynamic voltage stability； asynchronous motor； eigenvalue； index； time domain simulation

TM744； TM743

A

1003-8930(2012)01-0014-05

2010-12-16；

2011-03-03

国家科技支撑计划项目(2008BAA13B01)；国家自然科学基金重点项目(51037003)