经管类专业《统计学》教学中应融入数学模型思想

史文雷

（衡水学院，河北 衡水 053000）

统计学可分为理论统计学和应用统计学两类，前者侧重于统计方法的数学理论，后者侧重于统计方法在各个领域的应用。经管类专业学习的统计学课程侧重于统计应用，它是一门实践性和应用性很强的学科，是一门方法论科学。2002年2月，国家教育部高等教育司确立了包括统计学在内的8门课程为经济类专业的核心课程。鉴于此，很多关于经管类专业《统计学》教学的研究成果出现［1-3］，促进了教学改革与发展。由于经管类专业本身培养的特点，重应用、轻理论，一方面达到了培养要求，但另一方面也加深了对统计学问题的理解难度，忽视了统计学的模型化学习。本文针对几类统计学问题，从数学建模的角度，强化学生对于统计学的理解与学习。

一、数学模型化方法是统计学学习的基本方法

数学模型是从实际到抽象的一种方法，由于统计学的数量化这一特点，应用数学方法建立模型是其中基本的方法，也是解决统计学问题的必由之路。基本步骤为：

1.模型准备

针对一类有实际意义的统计学问题，通过收集资料，明确问题，把现实对象的问题，归纳为数学模型，从现实世界转化为数学世界。

2.建立模型

通过模型假设，依据数学模型分类，建立恰当的统计学数学模型，从而把实际问题转化成数学问题。

3.模型求解

利用对应的数学模型求解工具解决问题。

4.模型验证或判断

把数学问题的结论放到统计学实际中去应用、检验。

所以，从方法和步骤上看，研究实际问题，并对其进行数学描述，将其转化为数学模型问题进行求解，不仅是一种重要的科学研究方法，也是统计研究的基本方法。

二、几类统计学问题的数学模型化

1.参数估计的统计学模型

对于一个实际问题，建立统计学模型后，依据样本统计量去估计总体的参数，例如估计学生的上网时间、产品质量等。

例1：总体均值的区间估计（大样本）［4］

一家食品生产企业以生产袋装食品为主，为对产量质量进行监测，企业质检部门经常要进行抽检，以分析每袋重量是否符合要求。现从某天生产的一批食品中随机抽取了25袋，分别测得每袋重量。已知产品重量的分布服从正态分布，且总体标准差为10g。试估计该批产品平均重量的置信区间，置信水平为95%。

解：（1）模型准备：假定条件——总体服从正态分布，且方差（σ2）未知；如果不是正态分布，可由正态分布来近似（n≥30）；

（3）模型求解：总体均值μ在1-α置信水平下的置信区间为：

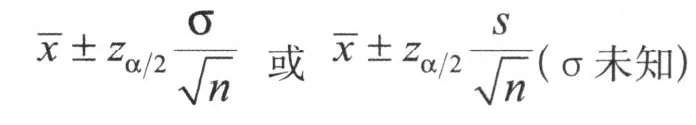
（4）模型检验：回到实际问题中，如结果不合适，可修改模型假设或重新找数据等。

2.假设检验的统计学模型

先对总体的参数（或分布形式）提出某种假设，然后利用样本信息判断假设是否成立。理论基础是运用反证法，统计上依据小概率原理。

例2：某企业声明有30%以上的消费者对其产品质量满意。如果随机调查600名消费者，表示对该企业产品满意的有220人。试在显著性水平α=0.05下，检验调查结果是否支持企业的自我声明。

解：（1）模型准备：假设条件——实际问题是满足正态总体还是非正态总体，选定原假设和备选假设。作出假设：ρ=30%，ρ>30%。

以上的备选假设是企业自我声明的结论，我们希望该企业说的是实话。因此使用右侧检验。

（2）模型建立：确定一个适当的检验统计量，并利用样本数据算出其具体数值。构造z检验统计量。

（3）模型求解：确定一个适当的显著性水平，并计算出其临界值，指定拒绝域，将统计量的值与临界值进行比较，作出决策，统计量的值落在拒绝域，拒绝H0，不拒绝H0。也可以直接利用P值作出决策。

确定拒绝域。显著水平α=0.05，查标准正态分布表得临界值：zα=1.645拒绝域是z>1.645。

计算检验统计量的数值。

样本成数p=220/600=0.37，总体假设的成数ρ=0.3，代入z检验统计量得：

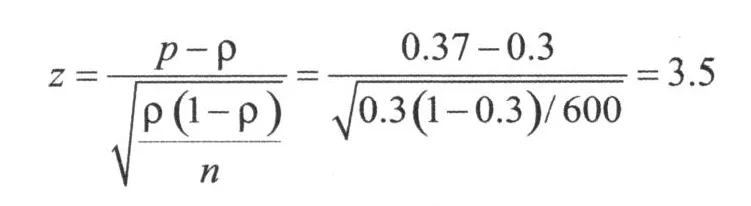
（4）模型检验：通过结果查看是否与经验和实际情况相符。

检验统计量的样本取值z=3.5>1.645，落入拒绝域。拒绝原假设，接受备选假设，认为样本数据证明该企业声明属实。

以上只介绍了统计学中两类问题的数学模型，对于统计学中的方差分析、回归分析、时间序列分析等问题也可以用类似的数学模型方法学习、讲解。

3.方差分析的数学模型

实例：消费者协会经常收到消费者与供应商之间纠纷的投诉，消协对几个行业分别抽取几家企业，统计最近一年中投诉次数，以确定这几个行业的服务质量是否有显著的差异。

某公司计划引进一条生产线，选择一条质量优良的生产线以减少日后的维修问题。下面以无交互作用的双因素方差分析为例。［5-6］

（1）模型准备：根据实际问题，建立假设：对因素A：μ1=μ2=μ3=μ4=μ5=…因素之间无差异，对因素B：μ1，μ2，μ3，μ4，μ5不全相等，因素之间有差异对因素B做同样假设。

（2）建立模型：构造MSA、MSB、MSE、F各自计算公式。

（3）模型求解：利用其计算公式求解。

（4）模型验证或判断：利用计算结果进行统计决策。

［1］ 刘华林，陶应奇.统计教学中的模型化方法研究［J］.绵阳师范高等专科学校学报，1999，（5）：17-20.

［2］ 李炳林.从统计创新谈经济管理类统计学教学改革［J］.时代教育，2008，（10）：123-124.

［3］ 吴明清.如何做好统计学课程教学改革［J］.职业时空，

2008，（11）：38.

［4］ 袁卫，等.统计学［M］.北京：高等教育出版社，2009.

［5］ 曾五一.统计学概论［M］.北京：首都经济贸易大学出版社，2006.

［6］ 刘金兰.管理统计学［M］.天津：天津大学出版社，2006.