二维结构纵向梁单元损伤识别
2012-11-06郭利
郭 利
(中铁十八局集团有限公司,天津 300222)
0 引言
结构发生损伤时,其损伤单元的刚度会发生改变,由于高阶模态对结构刚度矩阵影响的权重较大,而在实际测试中高阶模态却难以获取,因此人们提出用刚度矩阵的逆矩阵,即柔度矩阵作为损伤识别的参数。柔度矩阵比单纯的频率和振型对于结构损伤更为敏感,而且只需要低阶模态参数就可以得到较为准确的柔度矩阵,从而用于结构损伤辨别[1]。于是基于柔度矩阵的结构损伤辨别成为近阶段的热门课题,很多学者提出了有意义的识别方法和识别参数。
1 二维结构纵向梁单元柔度对角曲率
在结构动力学中,一直通过Cawley和Pandey假设[2]来简化模型,即假设结构损伤前后质量不变,不计前后阻尼的变化。在此前提下,只需要结构振动的各阶频率和质量归一后的振型就可以计算出结构的柔度矩阵。柔度矩阵Γ中元素fij表示在j点施加单位集中力导致i点产生的位移,而当结构在i点发生损伤时,在损伤单元施加单位集中力导致损伤单元的变形变化往往远大于其他位置,所以对于二维结构纵向梁单元拟采用柔度矩阵对角元素fii作为损伤识别的基本数据。由于二阶曲率对于损伤更为敏感,所以对fii做一次映射,用fii的二阶偏导数作为二维结构纵向梁单元的损伤指标,二维结构纵向梁单元测点i的柔度矩阵对角元素二阶偏导数为:

其中,li为同一纵梁相应的相邻两测点之间的距离,i的取值范围为对应纵梁的测点编号集(去除所在纵梁的第一个测点和最后一个测点),即假设纵梁Z的测点纵向编号依次为(n,n+1,Λ,n+k),则 i的取值范围为(n+1,n+2,Λ,n+k-1)。将同一根纵梁的各个测点的DFC值全部计算出来,依照测点位置顺序排列,作为纵梁损伤识别的参数。
2 二维结构纵向梁单元损伤识别的有限元模型
利用ANSYS分析软件,对一简支梁桥进行数值模拟,通过简支梁桥各纵梁损伤单元的弹性模量折减来模拟其纵梁发生损伤的状态,用模拟所得的简支梁桥的各测点的振型和频率计算对应测点的DFC值,作为损伤识别的指标,为了更好的模拟实际情况,检验指标的有效性,建立了一个较为复杂的ANSYS简支梁桥模型。对某简支梁桥的一跨进行建模,跨度20 m,宽9.5 m,纵向主梁为7根等截面空心板梁,横向连接浇筑成整体,再铺装沥青混凝土面层。纵向主梁采用Beam44梁单元建模,横向连接采用无质量的Beam44梁单元模拟,面层采用Shell93壳单元,面层与梁单元耦合成为整体。
单元参数设置为:
梁单元弹性模量取为EX1=3.3×1010Pa,密度设为dens1=2 600 kg/m3,泊松比设为σ1=0.2。壳单元弹性模量采用EX2=3.3×1010Pa,密度设为 dens2=2 500 kg/m3,泊松比设为 σ2=0.2。
其中梁单元编号如图1所示,测点编号如图2所示[3]。
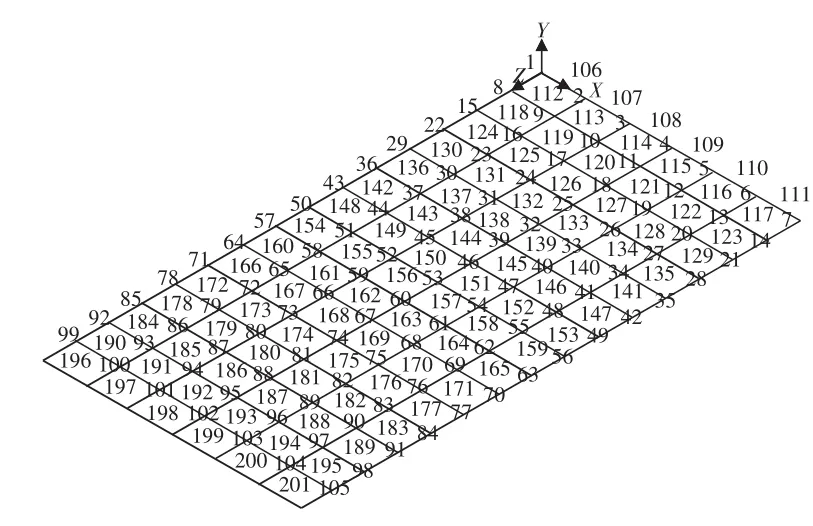
图1 梁单元编号

图2 测点编号
3 二维结构纵向梁单元的损伤识别
桥梁发生损伤时,以纵向主梁发生结构性损伤最为危险,因此主要研究纵向主梁损伤识别,纵向主梁的损伤通过纵向梁单元的弹性模量来模拟即将损伤单元的弹性模量取值为EX×(1-d),其中,d为单元的损伤程度[4]。对于边梁模拟了编号50的梁单元发生损伤时的情况,对于次边梁模拟了编号51的梁单元发生损伤时的情况,对于中梁模拟了编号53的梁单元发生损伤时的情况,对于次中梁模拟了编号52的梁单元发生损伤时的情况,梁单元所在位置如图1所示。
损伤情况均为损伤10%,30%,50%,70%,90%五种状况。边梁的测点编号为(1,2,3,Λ,16),次边梁的测点编号为(101,102,103,Λ,116),中梁的测点编号为(301,302,303,Λ,316),次中梁的测点编号为(201,202,203,Λ,216),测点位置如图2 所示。
由于高阶模态对于柔度矩阵贡献较小,故对于各损伤状态取其一阶频率和振型用来计算出柔度矩阵,然后计算出各测点所在纵梁的柔度矩阵对角元素二阶偏导数,其中边梁50单元发生损伤时的柔度对角曲率值如表1所示。
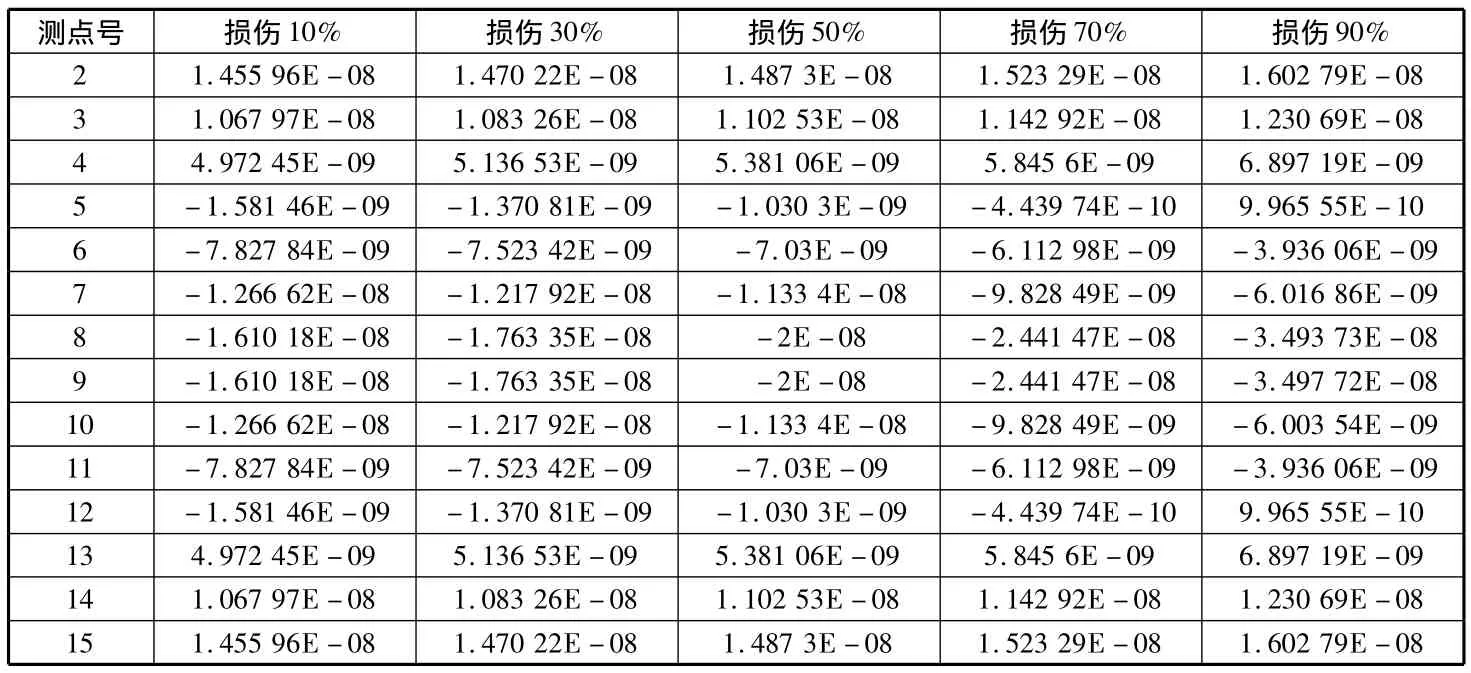
表1 边梁50单元损伤时的柔度对角曲率值
次边梁51单元发生损伤,次中梁52单元发生损伤,中梁53单元发生损伤柔度对角曲率值不再缀列。将边梁50单元发生损伤,次边梁51单元发生损伤,次中梁52单元发生损伤,中梁53单元发生损伤柔度对角曲率值绘成曲线图如图3~图6所示。
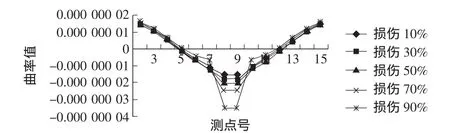
图3 边梁50单元发生损伤
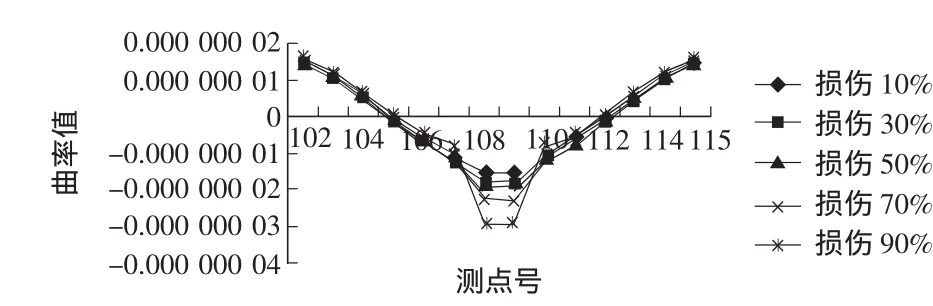
图4 次边梁51单元发生损伤
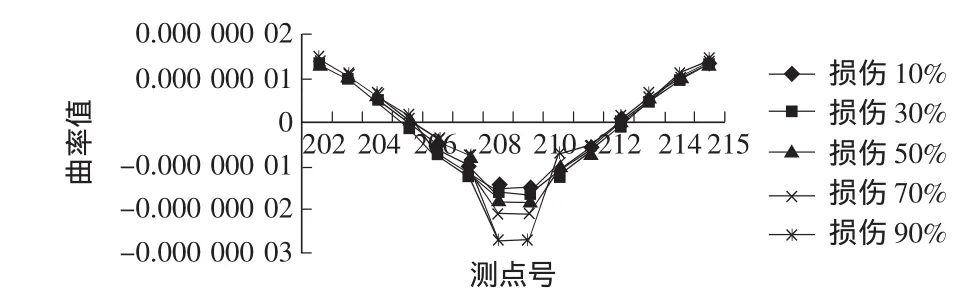
图5 次中梁52单元发生损伤
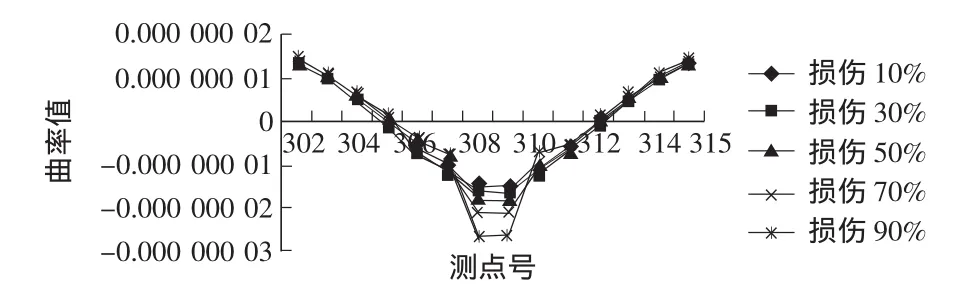
图6 中梁53单元发生损伤
从图3~图6中可以看出,当纵向主梁单元发生损伤时,不论是边梁还是中梁,其损伤单元附近测点的柔度对角曲率值的连续性将严重破坏,损伤位置十分容易辨别出来,而且可以看出随着损伤程度的加大,柔度对角曲率值的跳跃幅度也越大,损伤程度也是比较容易估计的。
从图中还可以看出边梁发生损伤时柔度对角曲率值的跳跃幅度最大,中梁最小,但即使是中梁,发生损伤时,其柔度对角曲率值的跳跃也是十分明显的。
4 结语
经分析可得以下结论:
1)对于二维结构纵向梁单元,柔度对角曲率指标具有很好的敏感性,能够准确反映损伤位置和程度;
2)二维结构纵向梁单元损伤识别时,柔度对角曲率指标对于数据的要求不高,只需要一阶模态数据就可以准确判断损伤位置以及对损伤程度进行初步估计,具有很好的实用性。
[1]冉志红.桥梁结构损伤识别的动力指纹方法研究[D].成都:西南交通大学博士学位论文,2007.
[2]Cawley P,ADAMSRD.The location of defects in structures from measurements of natural frequencies[J].Journal of Strain Analysis,1979,14(2):49,57.
[3]胡国良,任继文.ANSYS11.0有限元分析入门与提高[M].北京:国防工业出版社,2009.
[4]李永梅,周锡元,高向字,等.柔度曲率法对梁结构的损伤诊断[J].北京工业大学学报,2008,34(11):1173-1178.
