距离问题求解新探

王丽芳

（广州工程技术职业学院 广东 广州 510726）

距离问题求解新探

王丽芳

（广州工程技术职业学院 广东 广州 510726）

本文通过从几何角度对距离问题再认识，将距离与相切这两个概念沟通起来，形成一套求解距离问题的新办法，使优化思想在微分学中得以延伸。

距离;曲线族;曲面族;相切

引言

微分学中常把两个相离图形之间的距离问题归结为一个条件极值问题:即以两点间距离公式构成目标函数，以两个图形所满足的方程(或不等式)作为约束条件.这样的问题用拉格朗日乘数法足以解决。

本文另辟蹊径，抓住距离问题的实质，在几何上给予充分科学合理的解释，将问题予以适当转化，辅以微分学知识，提出了一种求解距离问题的直观准确的新解法.这种解法在理论上将导数与相切、距离与极值(含最值)等高等数学中几个核心概念进一步有机结合起来，令人更如深刻地领略数学领域里数形合一的无穷奥妙.同时将距离问题的求解与优化理论相沟通，使优化思想得到延伸，开拓了优化论更广泛的应用领域.这种解法在解决实际问题方面也是十分有效的，还可以让初学者拓广思路，开阔视野，提高学习兴趣。

1 距离问题的新解法

1.1 点到曲线的距离

定理1空间中的一点P到一条曲线L的距离等于以该点P为球心的球族中的一个与曲线L相外切的球的半径。

定理1为点到曲线距离问题提出了这样一个思路:首先以已知点为球心，取半径为参数K，构造球面族方程;再求球面与已知曲线的切点，最后求出相切球面的半径，即得所求距离。

实例 已知点P取为(x0,y0,z0),已知曲线L取为x=x(t),y=y(t),z=z(t),以P为球心的同心球面族方程为:

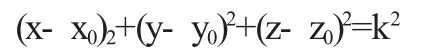
据微分学知识:已知曲线L上任一点(x,y,z)处切线的方向向量T={x'(t),y'(t),z'(t)},由球面与已知曲线相切，即得

其中x=x(t),y=y(t),z=z(t)

显然，这是一个关于t的一元方程，求解可得，t=t1

进而可得切点为(x(t1),y(t1),z(t1)),

再代入球面方程中可得出球面半径K，从而得所求的点到曲线距离.

注:待别地，若点P在曲线L上，则所求半径为0且切点恰是已知点.

推论：平面上一点P到一条曲线L的距离等于以点P为圆心的圆族中的一个与曲线L相外切的圆C。的半径.

定理2：空间中一点P到一条曲线L的最长距离等于以点P为球心的球族中的一个与曲线L相外切的球的半径.

注:1)若点P在曲线L上，则所求的点到曲线的最长距离仍可用定理2表述.

2)若曲线L延伸至无穷远处，则定理2中提及的“与曲线L相外切的球”实际是半径为无穷大的一个“球”。此时点P到曲线的距离为正无穷大.

推论：平面上一点P到一条曲线L的最长距离等于以点P为圆心的圆族中的一个与曲线L相内切的圆的半径.

例1抛物面z=x2+y2被平面x+y+z=1截成一椭圆，求原点到这个椭圆的最长距离和距离.

解：以原点为球心的球面方程为:x2+y2+z2=k2

其上任一点发向量为：{x，y，z}

据微分学知识，已知椭圆上任一点处的切向量为{2y十1，一2x-1,2x-y}

要求切点，则得方程:

x(2y+1)-y(2x+1)+z(2x-2y)=0

与z=x2+y2x+y+z=1联立

1.2 点到曲面的距离

定理3：空间中一点P到一个曲面的距离等于以点P为球心的球族中的一个与曲面相外切的球的半径.

实例 已知点P取为〈x。，y。，z。)已知曲面取为F(x,y,z)=o以P为球心的同心球面方程为(x-x。)2十(y-y。)2十('z-z。)2=0.其上任一点(x,y,z)处的切平面法向量已知曲面上任一点(x,y,z)处切平面法向量由球面与曲面S相切，即得，

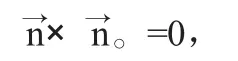
与曲面方程联立可求出切点，代入球面方程中可得球面半径K，即为所求的距离.

例2．求原点到曲面z2=xy+x-y+4的距离。

解:以原点为球心的球面万程为

x2+y2+z2=k2

其上任一点法向量为：{x，y，z}

又已知曲面上任一点处法向量

{y+1，x-1,-2z}

由“两相切曲面在切点处有同一切平面”

与z2=xy+x-y+4联立

解得x1=-1,y1=1,z1=-1;x2=-1,y2=1,z2=1代入球面方程得即所求距离。

2.距离问题新解法与优化思想的联系

本文所提诸法都是以某一已知图形为基准扩张生成的曲线(面)族，向另一图形搜索至相切位置，从而找出切点并得出结果的.这里进行扩张搜索的曲线(面)实质上是与基准图形距离相等的等值线(面),这种搜索方法与最优化问题图解法是一致的。这表明本文提出的距离问题新解法不失为优化思想又一新应用。

[1]同济大学数学教研室主编高等数学上册第六版2006.154~158

[2]同济大学数学教研室主编高等数学下册第六版2006.59~68

[3]李德钱颂迪 运筹学[M]北京:清华大学出版社 1982.70~81

New Exploration of the Distance Problem sSolving

WANGLi-fang
（Guangzhou Institute ofTechnology，Guangzhou 510726，Guangdong）

This paper fromthe perspective ofdistance geometryproblems,distance and tangent tothe twoconcepts ofcommunication,forma set ofnew approaches tosolvingproblems ofdistance,sothat the idea ofoptimization in differential calculus can be extended;

distance;curve;tangent surface family;tangent to

D157.3

A

1671-5004（2012） 01-0051-01

2012-2-19

王丽芳（1966-），女，广州工程技术职业学院高级讲师。