MATLAB PDE工具箱在稠油输送管道中的应用

张纯静，申龙涉，杜义朋，于丽丽，官学源，赵燕辉，张国军(辽宁石油化工

大学石油 天然气工程学院，辽宁 抚顺 113001)

石油化工

MATLAB PDE工具箱在稠油输送管道中的应用

张纯静，申龙涉，杜义朋，于丽丽，官学源，赵燕辉，张国军(辽宁石油化工

大学石油 天然气工程学院，辽宁 抚顺 113001)

利用Matlab PDE工具箱可以直接描绘出稠油输送管道中充分发展阶段的层流场，运行得到的参数与理论计算值相比误差很小，随着网格的精细化，更加接近于真实值，为管道内稠油的流动研究提供了一种直观、快速、准确、形象的数值求解方法。

Matlab PDE工具箱；稠油；偏微分方程；层流场

管道中层流黏性流动和紊流黏性流动是流体力学的常见问题，管道中稠油的流动为层流黏性流动。其中所用的稠油油样参数以辽河稠油为依据，半径为 35 mm稠油管道在输送中油温控制在 85 ℃左右，稠油在85 ℃时的动力黏性系数为850 mPa·s，轴向的压强梯度dP/dz为300 Pa/m，以此管道内稠油的流动为例，说明利用Matlab PDE工具箱如何求解水平管道中充分发展阶段的层流场。

1 Matlab PDE工具箱简介

在MATLAB命令[1]窗口中输入命令：pdetool，然后单击回车键，显示PDE图形用户界面。

一般地，利用PDE图形用户界面解决PDE问题的过程分为以下几步：

(1) 选择应用模式；

(2) 建立几何模型；

(3) 定义边界条件；

(4) 定义PDE类型和PDE系数；

(5) 三角形网格剖分；

(6) PDE求解；

(7) 解的图形表达；

(8) 数据输出。

2 基本原理

2.1 流体力学中层流沿轴向流场的微分方程

层流沿轴向流场的微分方程[2]

式中，u(y,z)是 轴方向上的速度，y和 是管道横截面的笛卡尔坐标[3]，点(0,0)是管道的中心点，管道壁的坐标(y,z)满足：

壁面处滞流[4]的边界条件为u=0。

2.2 Matlab PDE工具箱中的椭圆方程及边界条件

椭圆方程[5]为

式中，2Ñ 是Laplace算子[6]，u待解的未知函数，c,a,f是已知的实值标量函数。

在边界¶W上，方程的边界条件[7]一般可以写成：

Dirichlet条件(第一类边界条件)：hu=rNeumann条件(第二类边界条件)：

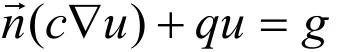
3 求解管内稠油输送

先利用Matlab PDE工具箱求解这个流场，再将计算出的流速最大值和平均值与解析法[8]求解结果相比较。以上面给出的稠油输送数据为参数，进行求解。

PDE类型[9]选定椭圆偏微分方程，即选中Elliptic单选钮，PDE参数的设定如图1所示，其中设定

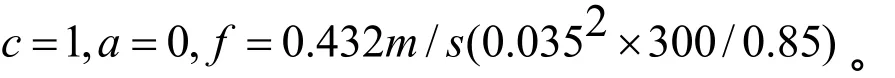
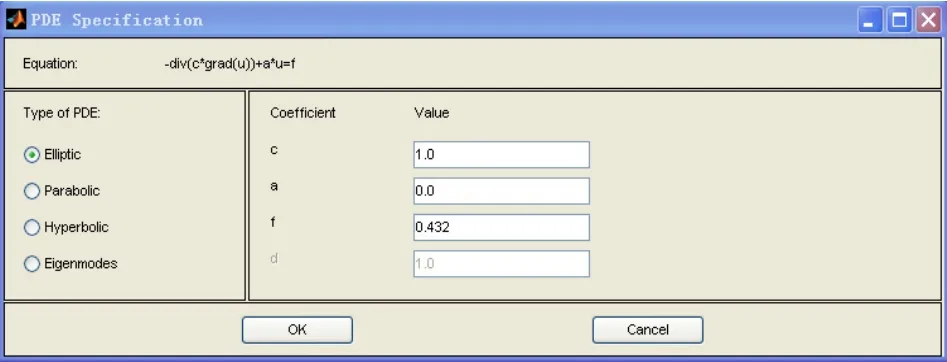
图1 稠油管道各个参数的设定图Fig.1 The basic parameter of heavy oil pipeline

初始化网格5次，每次网格化后并对其进行微调，其最后的结果以等高线的形式绘出，如图2所示。

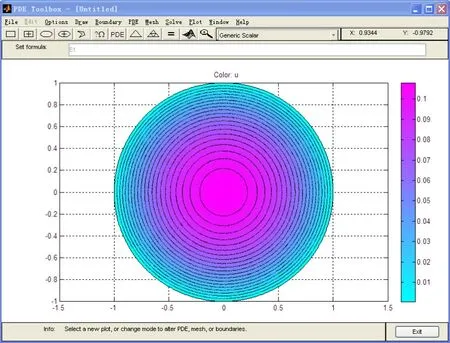
图2 圆形管道内稠油流动的速度场等值线图最内层等高线的数值为0.1Fig.2 Contours of velocity field of viscous flow in circular pipe Innermost value of contour is 0.1

图2中任何节点处的速度u皆可求出，将网格描述的量p,e,t及求解结果u输出在 Matlab命令的窗口中， 给出了网格的坐标点，e描述述了格状三角形的边缘，t描述角度。由于将会输出大量的数据，通常取特殊点进行验证。从图2可见，速度的最大值出现在管道横截面的中心点处，为求得该值，在Matlab命令窗口输入语句：

还可以绘出速度与管道直径的函数图形，首先必须用 tri2grid函数[10]将三角网格数据添加到位于管道横截面半径的点上。在 MATLAB窗口中输入以下代码：

得到结果如图3所示。

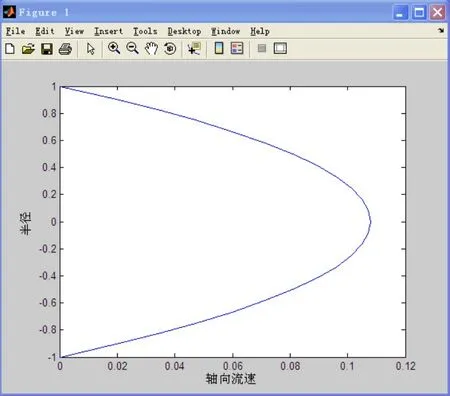
图3 管道内稠油流动的轴向流速与半径的位置关系图Fig.3 The relationship of axial velocity and the radius of viscous flow in the pipeline

4 结 论

MATLAB提供了一个图形用户界面的偏微分方程数值求解工具，利用该工具可以较形象地描绘出水平输送管道中运动稠油充分发展的层流场，比较准确的计算出管道流量，并绘制出了轴向流速与半径的位置关系，从而把抽象的公式理论与形象的图形联系起来。

［1］ 苏金明,张莲花,刘波. MATLAB工具箱应用[M].北京：电子工业出版社, 2004.

［2］ 马贵阳. 工程流体力学[M]. 北京：石油工业出版社, 2009.

［3］ 袁恩熙. 工程流体力学[M]. 北京：石油工业出版社, 2007.

［4］ 兰州炼油厂. 管式加热炉[M]. 北京： 燃料化学工业出版社,1974,12-14.

［5］ 田兵. 用MATLAB解偏微分方程[J]. 阴山学刊, 2006,20(4)：12-13.

［6］ 贺超英. MATLAB应用与实验教程[J].北京：电子工业出版社,2010,37-80.

［7］ 李明. 偏微分方程的 MATLAB解法[J]. 湖南农机, 2010,37(3)：89-91.

［8］ 陆金甫,关治. 偏微分方程的数值解法[M]. 北京：清华大学出版社2004.

［9］ 高会生,李新叶,胡智奇，等译. MATLAB 原理与工程应用(第二版)[M]. 北京：电子工业出版社, 2006：274-282;419-429.

［10］ 龚纯,王正林. MATLAB语言常用算法程序集[M].北京：电子工业出版社, 2007.

Application of MATLAB PDE Toolbox in Pipeline Transportation of Heavy Oil

ZHANG Chun-jing，SHEN Long-she,DU Yi-peng, YU Li-li, GUAN Xue-yuan, ZHAO Yan-hui, ZHANG Guo-jun
（Academy of Petrol and Natural Gas Engineering, Liaoning Shihua University, Liaoning Fushun 113001, China）

Using Matlab PDE toolbox can depict the laminar flow field of the full development stages in heavy oil pipeline. Compared with theoretical calculation results, error of gained parameters is small. With refinement of the grid,the gained parameters are closer to the true value, which can provide a fast, accurate numerical solution for studying the flow of heavy oil in pipeline.

Matlab PDE toolbox; Heavy oil; Partial differential equations; Laminar flow field

TE 832

A

1671-0460（2012）01-0048-03

2011-11-07

张纯静（1984-），男，山东菏泽人，2006年毕业于滨州学院数学与信息科学系，现为辽宁石油化工大学在读硕士，研究方向：稠油集输系统工艺技术研究。E-mail：zchunjing@126.com。