火灾作用下隧道衬砌结构变形理论分析模型

李忠友，刘元雪，刘树林，谭仪忠，葛增超

（1.后勤工程学院 建筑工程系，重庆 401311；2.后勤工程学院 岩土力学与地质环境保护重庆市重点实验室，重庆 401311；3.广州军区 空军后勤部，广州 510010）

1 引 言

隧道因其在穿越障碍，提高交通能力，节约土地资源，加强城市防护等方面的巨大优势，日益受到各国的青睐，我国的隧道建设更是日新月异。然而，随着隧道在人们生产、生活中发挥的作用越来越大，应用越来越广，其潜在的灾害也逐渐得到了更多的重视，尤其是隧道火灾，由于其具有升温速度快、温度高、持续时间长等特点，一旦发生，往往会造成衬砌混凝土力学性能的严重劣化，进而引起结构承载力的降低和变形量的增大，甚至诱发隧道坍塌等灾难性的破坏[1－3]，因此，对于火灾作用下的隧道结构变形行为等问题进行深入研究，具有重要的理论意义和工程应用价值。

当前在混凝土结构在火灾等高温作用下变形行为的理论研究已取得了一定的进展。李世荣等[4]基于几何非线性理论和打靶法，研究了两端不可移简支弹性梁在横向非均匀分布升温场作用下的热弹性屈曲变形响应。Bradford等[5]利用几何和材料非线性理论，分析高温作用下混凝土扁平拱结构的变形行为。由于结构形式及荷载分布的不同，上述研究成果不能直接用于火灾作用下隧道结构的变形分析，且计算过程中均假设温度在结构中呈线性规律变化，显然与实际情况不符。

本文在Bradford等的研究基础上，综合考虑衬砌结构中温度场的非线性分布，材料高温力学性能的劣化以及材料热膨胀等因素的影响，提出了适用于描述火灾作用下隧道衬砌结构变形行为的理论分析模型，并给出了半圆形隧道在火灾作用下截面转角及径向变形的解析解。结合算例，分析了不同火灾持续时间作用下隧道衬砌竖向变形和横向变形的变化规律。

2 衬砌变形理论分析模型

现有试验表明，在高温作用下混凝土的弹性模量降低，峰值应变增大，但材料在屈服前仍能满足弹性变形条件，考虑本文主要研究衬砌结构在火灾作用下的变形规律，根据隧道火灾的实际情况，为简化问题，特作如下假定：（1）衬砌结构的截面变形满足平截面假定；（2）混凝土未屈服，材料处于弹性变形阶段。

根据假定（1），将隧道衬砌简化为拱结构，其截面为单位宽度的矩形，高与衬砌厚度相同，如图1所示。图中，Tb为衬砌内表面（受火面）温度；Tt为衬砌外表面温度；h为衬砌厚度。当满足平截面假定时，衬砌截面上应变可以表示为

式中：y0为中性轴的位置；κ为截面曲率。

图1 衬砌截面上应变与温度分布Fig.1 Distribution of strain and temperature on lining cross-section

混凝土在高温作用下会产生热膨胀，由热膨胀引起的应变为

式中：k为混凝土的热膨胀系数；T(y)为衬砌内的分布函数。

由式(1)、(2)可得到横截面上弹性应变：

不考虑隧道纵向上的温度变化，根据假定(2)可得截面上的应力为

式中：ET为混凝土的弹性模量，与温度及混凝土类型等因素有关。由式(4)可以得到单位宽度矩形衬砌截面上的轴力N：

式中：h为衬砌的厚度。

结合式(4)和式(5)，可以确定高温作用下衬砌截面中性轴的位置为

由式(4)得到单位宽度矩形衬砌截面所承受的弯矩可以表示为

由式（7）整理可得到衬砌截面曲率的表达式：

式中：α1、α2、α3、α4为与衬砌截面上温度分布及弹性模量变化相关的参数，分别为

对于拱形结构，其截面转角的改变量可以用截面曲率近似表示[6]，因而简化后的隧道衬砌结构的截面转角可以表示为

式中：s为相对于衬砌拱顶的弧长。

根据衬砌的截面转角与径向变形之间的关系，可以得到衬砌结构径向变形表达式：

由式(11)可以进一步得到隧道衬砌结构的横向位移和竖向位移分别为

式中：R为隧道半径，s为位移。

值得注意的是，由于弹性模量的变化，轴力发生偏心作用，将引起附加弯矩，因而有

对于复杂结构问题，可以通过 MatLab等数学软件对式(10)和式(11)进行求解，分析火灾作用下隧道衬砌结构的变形行为。对于半圆形隧道等简单结构问题，可以对式(10)和式(11)直接积分求得衬砌结构变形行为的解析解。

3 半圆形隧道变形解析解

将半圆形隧道衬砌结构简化为两端铰接的超静定拱，作用在衬砌结构上的荷载如图2所示，因而衬砌横截面上的轴力可以写为

作用在衬砌横截面上的弯矩为

图2 衬砌结构荷载分布图Fig.2 Distribution map of loads on the lining structure

由于隧道空间狭小，对于公交车、货车等大型车辆引发的火灾事故，在衬砌表面温度近似于均匀分布[7]，因而根据同济大学的研究成果，衬砌内温度分布可以表示为[8]

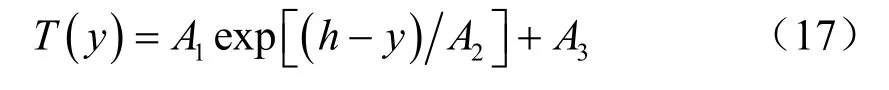
式中：Ai(i=1,2,3)为与衬砌厚度、火灾持续时间及衬砌表面温度相关的参数。

混凝土材料在高温作用下其内部结构会发生物理、化学损伤，导致其力学性能劣化，当前的研究成果表明[9]，混凝土弹性模量随温度的变化规律基本呈线性变化。因而在本文中，定义衬砌混凝土的弹性模量随温度的变化表达式为

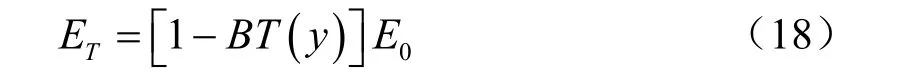
式中：B为与材料属性相关的常数，本文取0.001。

结合式(10)、(12)和式(13)第二式，可以得到半圆形衬砌结构的截面转角解析表达式：

式中：ζi=i R+h ；ξi=i R-h，i为虚数。由式(11)可得到衬砌结构的径向位移为

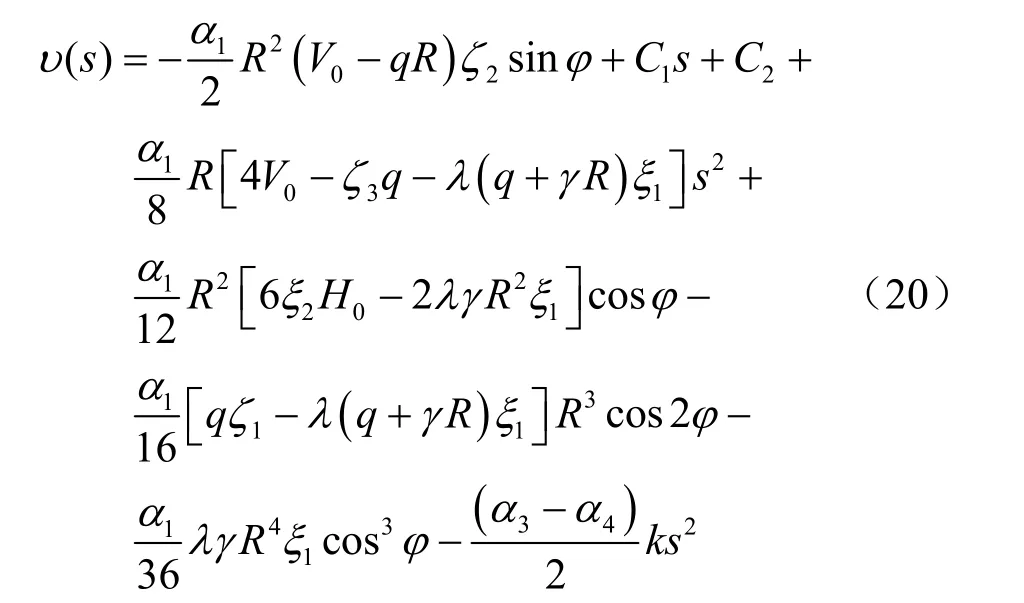
式中：C1、C2为常数，由边界条件可以确定。在本文算例中，衬砌两端为铰接，因而变形为 0，即当φ=90°时，υ(s)=0；φ=-90°时，υ(s)=0。将上述关系分别代入式(20)，可得

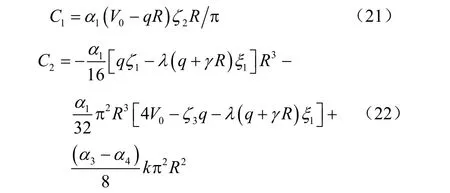
将式(20)计算结果代入式(12)，可以得到衬砌横向位移ux（s）和竖向位移uy（s）。

4 算例分析

隧道埋深为30 m，衬砌为半圆形，厚0.35 m，围岩重度γ=25 kN/m3，泊松比λ= 0.3，混凝土衬砌弹性模量E=29.5 GPa，火灾最高温度为1 000℃。按前文给出的方法，计算结果见图3～5。

图3 衬砌结构竖向位移变化曲线Fig.3 Curves of vertical displacement of lining structure

图4 衬砌结构横向位移变化曲线Fig.4 Curves of transversal displacement of lining structure

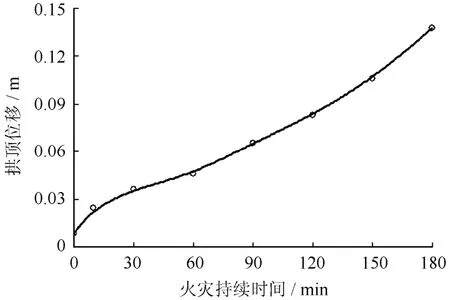
图5 衬砌结构拱顶位移变化曲线Fig.5 Curves of arch crown displacements of lining structure

衬砌结构竖向位移曲线如图3所示，拱顶两侧衬砌竖向位移呈对称性分布，随火灾持续时间的拱顶两侧竖向位移逐渐增大，在火灾持续时间为 30 min时，最大竖向位移为3.2 cm，到火灾持续180 min后，最大竖向位移达到13.5 cm。衬砌结构横向位移曲线 如图4所示，拱顶两侧衬砌横向位移呈反对称性分布，随火灾持续时间的拱顶两侧横向位移逐渐增大，在火灾持续时间为30 min时，隧道两侧横向位移为0.4 cm，到火灾持续180 min后，隧道两侧横向位移达到1.7 cm，与竖向位移最大值相比，横向位移最大值相对较小。衬砌结构拱顶位移曲线如图5所示，随火灾持续时间的增加，拱顶位移逐渐增大，在火灾发生后30 min时，拱顶位移变化曲线出现转折点，此后拱顶位移增速随时间增长逐渐增大，灾后180 min时拱顶位移已达到灾后30 min时拱顶位移的4.2倍。

5 结 语

基于几何和材料非线性理论，提出了适用于描述火灾作用下隧道衬砌结构变形行为的理论分析模型，并给出了半圆形隧道衬砌变形的解析解。

通过算例分析了火灾作用下衬砌结构的变形行为，得到了火灾持续时间对隧道整体竖向位移、横向位移及拱顶位移的影响规律，计算结果可以为火灾作用下隧道安全防护及评估提供理论指导。

[1] GUIAN S K.Fire and life safety provisions for a long vehicular tunnel[J].Tunnelling and Underground Space Technology, 2004, 19: 316－316.

[2] MASHIMO H.State of the road tunnel safety technology in Japan[J].Tunnelling and Underground Space Technology, 2002, 17(2): 145－152.

[3] SCHREFLER B A, BRUNELLO P, GAWIN D, et al.Concrete at high temperature with application to tunnel fire[J].Computational Mechanics, 2002, 29(l): 43－51.

[4] 李世荣, 程昌钧, 周又和.横向非均升温下弹性梁的热过屈曲[J].应用数学和力学, 2003, 24(5): 455－460.LI Shi-rong, CHENG Chang-jun, ZHOU You-he.Thermal post-buckling of an elastic beams subjected to a transversely non-uniform temperature rising[J].Applied Mathematics and Mechanics, 2003, 24(5): 455－460.

[5] BRADFORD M A.In-plane stability of pinned arches with elastic restraints under thermal loading[J].International Journal of Structural Stability and Dynamics, 2006, 6(2): 163－177.

[6] HEIDARPOUR A, PHAM T H, BRADFORD M A.Nonlinear thermoelastic analysis of composite steelconcrete arches including partial interaction and elevated temperature loading[J].Engineering Structures, 2010,32: 3248－3257.

[7] 阎治国.隧道衬砌结构火灾高温力学行为及耐火方法研究[D].上海: 同济大学, 2006.

[8] 强健.地铁隧道衬砌结构火灾损伤与灾后评估方法研究[D].上海: 同济大学, 2007.

[9] 过镇海, 李卫.混凝土在不同应力-温度途径下的变形试验和本构关系[J].土木工程学报, 1993, 26(5): 58－69.GUO Zhen-hai, LI Wei.Deformation testing and constitutive relationship of concrete under different stress-temperature paths[J].China Civil Engineering Journal.1993, 26(5): 58－69.