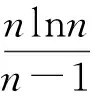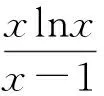换元引参与整体思想在高考中的应用

●

(湖州中学 浙江湖州 313000)

换元引参与整体思想在高考中的应用

●蒋际明

(湖州中学 浙江湖州 313000)

换元引参与整体思想内涵丰富，它渗透到数学的各个领域，是体现学生观察能力、直觉思维能力和整体意识的主要思想方法，同时也能体现学生思维结构中从大处着眼的宏观调控能力.换元引参是整体思想的集中体现，在整体思想中扮演着不可或缺的角色.通过换元引参可以将陌生的、不能处理的问题转化为熟悉的、可以解决的问题，也体现了转化与化归的思想.

解决数学问题的过程中，有时为了将陌生、抽象、复杂的问题转化为熟悉、具体、简单的问题，促使未知向已知转化，常将某个式子看作一个整体，引入一个新的变量，用一个字母来代替它，实行变量代换，从而使问题得到解决，这种解决问题的方法叫做换元引参.

利用换元引参解题的关键在于选择适当的辅助未知数，要注意2个方面：一是字母之间、式子之间的转化；二是变量代换时范围的取舍.一定要注意新变量的取值范围、换元所受的限制条件，特别是要挖掘隐含的限制条件，还要注意根据题设条件来验证结果.

将需要解决的问题看作一个整体，通过研究问题的整体形式和整体结构，并通过对整体结构的调节和转化使问题获解，这种从整体观点出发研究问题的思维活动过程称为整体思想.整体思想具体可分为整体观察、整体代入、整体构造、设而不求等，在解题时，要从问题的条件出发，抓住整体结构，使问题转化为熟悉的数学模型，从而解决问题.

换元引参和整体思想是数学转化能力的一种体现，它渗透于数学的方方面面，在历年高考试题中都有考查.

1 典型例题

1.1 局部换元

例1已知集合A={x|4x-2x+1+a=0,x∈R}，若集合A中有且只有1个元素,求实数a的取值范围.

分析令t=2x，则t>0，方程4x-2x+1+a=0可化为

t2-2t+a=0.

点评通过换元，把超越方程转化成了熟悉的二次方程来求解，简化了问题.这里要特别注意的是原方程有一个根并不与所转化的二次方程有一个根等价，由于辅助元取值为正数，因此等价于二次方程有一个正根.

1.2 整体换元

例2设x,y为实数，若4x2+y2+xy=1，则2x+y的最大值是________.

(2011年浙江省数学高考理科试题)

解设2x+y=t，则

y=t-2x,

代入4x2+y2+xy=1中得

6x2-3tx+t2-1=0,

将它看作一个关于x的二次方程，则由判别式大于等于0，可得

Δ=(3t)2-4·6·(t2-1)≥0,

解得

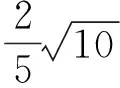
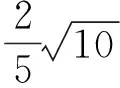
点评将2x+y视为一个整体并引入参数t，进而通过消元把问题转化为二次方程有实数根的问题，此类方法在历年高考题中时有出现.

1.3 三角换元

从而

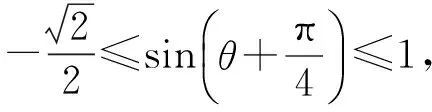
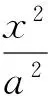
1.4 均值换元

例4已知正数x,y满足x+y=1,求证：

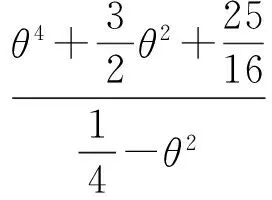
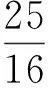
原不等式得证.

点评若已知2个变量的算术平均值，可采用均值换元法，使原来的2个变量转化为只含有1个变量的问题，从而达到减少变量的目的，且使变量间的关系更加明显.

1.5 设点引参

(1)当直线l过右焦点F2时，求直线l的方程.

(2)设直线l与椭圆C交于点A,B，△AF1F2，△BF1F2的重心分别为G,H.若原点O在以线段GH为直径的圆内，求实数m的取值范围.

(2010年浙江省数学高考理科试题)

(2)设A(x1,y1),B(x2,y2),由

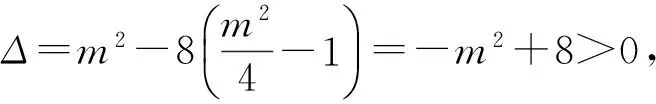
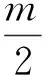
从而

化简得

x1x2+y1y2<0,

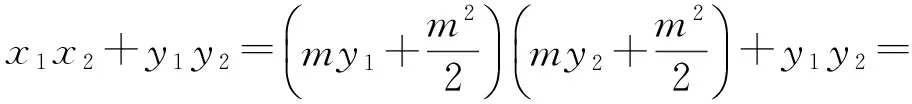
点评本题虽有多种解法，但都离不开点A，B的坐标参与，故引参时必须考虑设点A，B的坐标(设而不求).在具体消参运算时，将x1x2，y1y2，x1+x2，y1+y2作为一个变量(整体)考虑，这给消参带来了便利.

1.6 整体观察

分析(1)先将结论因式分解，然后将a0+a1+a2+a3+a4和a0-a1+a2-a3+a4都看作整体进行运算，分别令x=1，x=-1，易得结果为1.

1.7 整体构造

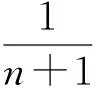
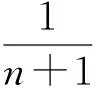
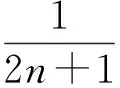
于是f(n)是定义域上的单调递增函数，从而

解得

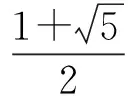
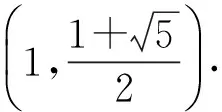
点评在这里构造函数是为了求f(n)的最小值，对于恒成立的问题,函数最值解法是一种非常有效的方法.要注意总结一些解题的小结论，例如要使f(n)≥g(a)恒成立，只须[f(n)]min≥g(a)即可等等.

图1

1.8 整体代入

(1)求曲线C的方程；

(2008年浙江省高考数学理科试题)

分析(1)容易得到曲线C的方程为

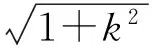
在Rt△QMA中，因为

所以

于是

得

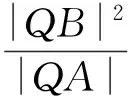
换元引参与整体思想是最基本、最常用的数学思想.它是通过研究问题的整体形式、整体结构，并对其进行调节和转化使问题获解的一种方法．简单地说就是从整体去观察、认识问题,从而解决问题的思想.它是数学解题中一个重要而有效的策略，是提高解题速度的有效途径.

2 精题集萃

( )

2.长方体的全面积为11，12条棱长度之和为24，则长方体的对角线长为

( )

A．6 B．5 C．4 D．3

( )

4.已知sin3θ+cos3θ=1，则sinθ+cosθ的值为

( )

5.若(1+2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a0+a1+a3+a5=

( )

A.122 B.123 C.243 D.244

6.已知等差数列{an}的前n项的和为100，前4项的和为16，后4项的和为64，则n=________.

9.当n>m>1,(n,m∈Z)时，证明：(mnn)m>(nmm)n.

参考答案

1.C 2．B 3．A 4．D 5．B 6.n=10 7.8

8.解显然直线x=0不满足题设条件，可设l的方程为y=kx+2.设A(x1,x2),B(x2,y2)，联立

从而

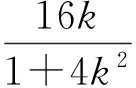
Δ=(16k)2-4·(1+4k2)·12=64(4k2-3)>0，

得

由∠AOB为锐角，得

而y1y2= (kx1+2)(kx2+2)=

k2x1x2+2k(x1+x2)+4，

从而

x1x2+y1y2= (1+k2)x1x2+2k(x1+x2)+4=

解得

-2

9.证明要证(mnn)m>(nmm)n，即证

mlnm+nmlnn>nlnn+nmlnm，

即

从而g(x)在(1,+∞)上是增函数，而g(1)=0，可知

g(x)=x-1-lnx>0,

于是

φ′(x)>0,

即y=φ(x)是增函数.又n>m>1，得

φ(n)>φ(m),

从而

(mnn)m>(nmm)n.