高考中的函数与方程思想
2012-11-06
●
(杭州市第二中学 浙江杭州 310053)
高考中的函数与方程思想
●徐存旭
(杭州市第二中学 浙江杭州 310053)
思想即理性认识,是相对于感性认识而存在的,是对于感性认识加工的结果.函数思想,即用运动和变化的观点、集合与对应的思想,分析和研究数学问题中的数量关系,利用函数知识或函数观点观察、分析问题,建立函数关系或构造函数,运用函数的图像和性质去分析问题、转化问题,从而解决问题.方程思想,就是分析数学问题中变量间的等量关系,运用数学语言将问题中的条件转化为数学模型,运用方程的性质去分析、转化问题,使问题获得解决.
函数思想与方程思想都是用运动、联系和变化的观点来看数学问题.函数与方程、不等式是通过函数值等于0、大于0和小于0而相互关联的,二者之间既有区别又有联系.
1 考查要求
函数与方程思想是中学数学的基本思想,也是历年高考的重点,在选择、填空和解答题中都有涉及.选择和填空题中更多的是思想方法的基本运用,在解答题中,则从更深的层次、在知识网络的交汇处,从思想方法和相关能力的关系角度综合考查.函数在中学数学中的地位决定了函数与方程思想成为核心的思想,也成为高考考查的重点.
2 考点回顾
纵观历年考题可以发现,函数与方程思想是每份高考试卷必考的内容.如2011年浙江省数学高考理科试卷中,涉及到函数与方程思想的题目有第5,6,8,10,13,14,16,17题,在解答题中几乎都有涉及,占有重要的地位.其他年份考查的频率也基本相当.
3 典例剖析
例1设a,b,c为实数,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若|S|,|T|分别为集合S,T的元素个数,则下列结论不可能的是
( )
A.|S|=1且|T|=0 B.|S|=1且|T|=1
C.|S|=2且|T|=2 D.|S|=2且|T|=3
(2011年浙江省数学高考理科试题)
分析将方程进行分解,分别考虑类似的方程因式.对于“x+a=0”与“ax+1=0”,前者的零点个数为1,后者当a≠0时,零点个数为1,当a=0时零点个数为0.对于“x2+bx+c=0”与“cx2+bx+1=0”,当c=0时,若b=0,前者的零点个数为1,后者的零点个数为0,若b≠0,前者的零点个数为2,后者的零点个数为1;当c≠0时,注意到2个方程的判别式Δ相等,零点的个数即根的个数相等.结合选项知a=0,Δ=b2-4c<0,即选项A成立;当a≠0,Δ=b2-4c<0,选项B成立;当a≠0时且Δ=b2-4c=0,选项C可能成立(如a=1,b=c=4).若|T|=3,则a≠0且c≠0,Δ=b2-4c>0,则|S|=3必成立.故选D.
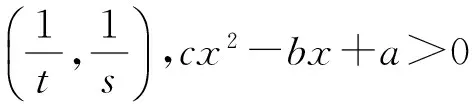

( )

(2008年浙江省数学高考理科试题)
分析这是三角函数中典型的给值求值的一类问题.已知条件中涉及2个量sinα,cosα,注意到sinα和cosα的一个隐含关系cos2α+sin2α=1,应用方程的思想,构造关于sinα和cosα的方程组,可以求得sinα和cosα的值,从而可得tanα的值.

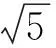
即
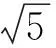
从而


f′(α)=-sinα+2cosα=0,
得tanα=2.故选B.
评注注意到已知条件中量的个数和关系,应用方程的思想可以分别求出sinα和cosα的值,进而求得tanα的值,这是方程思想.对一般的问题“asinα+bcosα=c”,运用此思想和方法,均可求tanα的值或判断其值是否存在.注意到题中特殊的数量关系,通过构造函数,利用函数取得极值的条件,便可求解.其实,一道试题,都是一类问题的“共性”和“个性”的统一,如果能充分地注意到这一点,利用合适的数学方法和思想进行思考,往往能收到事半功倍的效果.
例3已知集合
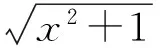
则集合M表示的图形是
( )
A.直线 B.线段 C.抛物线 D.圆
分析本题若通过平方化简方程,运算较为复杂,可以从函数和变量的角度进行思考.

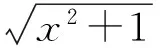
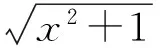
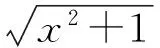

lg1=0,
从而g(x)=-g(y),得x=-y,即x+y=0.
如果注意到已知条件中等式的代数结构,可以考虑其共轭式,构造方程来求解.
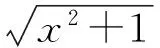
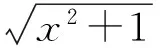
即s,t分别是方程
s2-2xs-1=0,t2-2xt-1=0
的正根,整理得

2式相加,结合st=1,得

即
x+y=0.
评注上述3种思路或构造函数,或显化方程的关系,减少了计算量,这契合了高考“多考点想,少考点算”的命题原则,也从另一个方面说明在函数与方程思想的指引下,为寻找解题思路、简化解题过程提供了可能.当然,注意到本题是一道选择题,还可以通过做选择题的技巧,如代值法求解,令x=-1,0,1,分别得y=1,0,-1,否定选项C,D,注意到x,y的取值范围为R,即得选项A.

(1)求椭圆G的焦点坐标和离心率;
(2)将|AB|表示为m的函数,并求|AB|的最大值.
(2011年北京市数学高考理科试题)

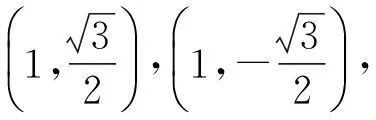
(1+4k2)x2-8k2mx+4k2m2-4=0.
设点A,B的坐标分别为(x1,y1),(x2,y2),则

又l与圆x2+y2=1相切,得
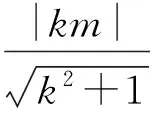
即
m2k2=k2+1,



又
m∈(-∞,-1)∪(1,+∞),
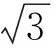
评注解析几何中考查弦长或面积的最值问题是高考中的重点和热点,求解的关键是建立弦长或面积的目标函数,应用函数或不等式知识求解最值.
例5设函数f(x)=(x-a)2lnx,a∈R.
(1)若x=e为y=f(x)的极值点,求实数a;
(2)求实数a的取值范围,使得对任意的x∈(0,3e],恒有f(x)≤4e2成立.
(2011年浙江省数学高考理科试题)
分析第(1)小题通过求导得


因为x=e是f(x)的极值点,所以
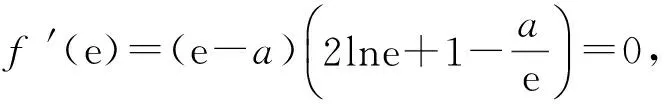
第(2)小题,注意到只需考虑当x∈(1,3e]时,(x-a)2lnx≤4e2成立即可.令x=e,代入f(x)≤4e2得
(e-a)2≤4e2,
解得
-e≤a≤3e.
当x∈(a,3e]时,f(x)单调递增,则
f(3e)≤4e2
整理得
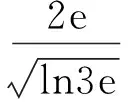
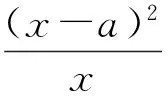
4x2(lnx)3≤4e2,

评注导函数的综合问题是2011年浙江省数学高考的压轴题.结合指数、对数函数应用导数工具求最值或求参数的取值范围是高考设问的热点.应用函数与方程的思想,列出方程,构造辅助函数是求解此类问题常用的方法.
4 精题集萃
1.函数f:{1,2,3}→{1,2,3}满足f(f(x))=f(x),则这样的函数个数共有
( )
A.1个 B.4个 C.8个 D.10个

( )

( )
A.-6 B.6 C.-7 D.7
( )
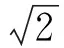
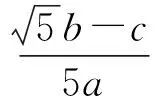
( )
A.b2>4acB.b2≥4ac
C.b2<4acD.b2≤4ac

7.已知平面向量满足α,β(α≠0,α≠β),满足|β|=1,且α与β-α的夹角为120°,则|α|的取值范围是________.
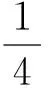
(1)求sinC的值;
(2)当a=2,2sinΑ=sinC时.求b及c的长.
9.设函数f(x)=x3+2ax2+bx+a,g(x)=x2-3x+2,其中x∈R,a,b为常数,已知曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l.
(1)求a,b的值,并写出切线l的方程;
(2)若方程f(x)+g(x)=mx有3个互不相同的实根0,x1,x2,其中x1 参考答案 1.D 2.C 3.B 4.C 5.B 从而 9.解(1)切线l的方程为x-y-2=0. (2)由第(1)小题得 f(x)=x3-4x2+5x-2, 所以 f(x)+g(x)=x3-3x2+2x. 由题意,方程x(x2-3x+2-m)=0有3个互不相同的实数0,x1,x2,因此x1,x2是方程x2-3x+2-m=0的2个相异的实根,从而 Δ=9-4(2-m)>0, 即 对任意的x∈[x1,x2],f(x)+g(x) f(x1)+g(x1)-mx1<-m 成立,得m<0.由韦达定理得 x1+x2=3>0,x1x2=2-m>0, 故 0 对任意的x∈[x1,x2],有 x-x2≤0,x-x1≥0,x>0, 则 f(x)+g(x)-mx=x(x-x1)(x-x2)≤0. 又f(x1)+g(x1)-mx1=0,故f(x)+g(x)-mx在x∈[x1,x2]的最大值为0.于是当m<0时,对任意x∈[x1,x2],f(x)+g(x)