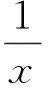“算两次”的思想方法——解决数学问题的一把金钥匙

●

(杭州学军中学 浙江杭州 310012)

“算两次”的思想方法
——解决数学问题的一把金钥匙

●郑日锋

(杭州学军中学 浙江杭州 310012)

美国数学教育家波利亚说“为了得到一个方程，我们必须把同一个量以两种不同的方法表示出来”，即将一个量“算两次”，从而建立相等关系，这就是算两次原理，又称富比尼(G.Fubini)原理．单墫教授在文献[1]中，将算两次原理形象地比喻成“三步舞曲”，即从2个方面考虑一个适当量，“一方面……，另一方面……，综合起来可得……”，如果一个数学研究对象具有“双重身份”或“两面性”，也就是说既满足条件A又满足条件B，就可以考虑使用这种方法．

“算两次”是从不同角度看问题的另一种说法，是一种常用的数学方法，它体现了数学的转化思想、方程思想.本文阐述“算两次”思想在解题中的作用．

1 建立方程(等式)

通常的列方程其实就是一种“算两次”．2个方面考虑的是同一个量，因此结果相等，这就产生了方程(等式)．许多数学公式的推导可以运用“算两次”思想，如两角和的余弦公式的向量方法证明．

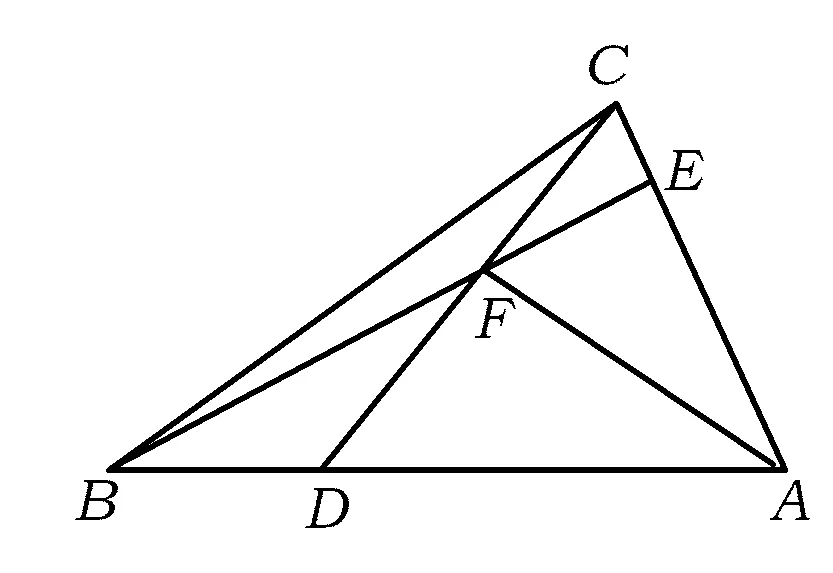
图1

解因为点B，F，E共线，所以存在实数m，使

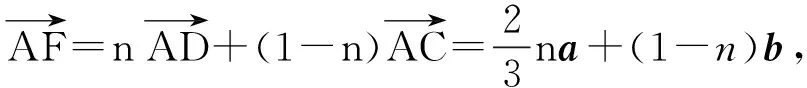
因此

由平面向量基本定理，得

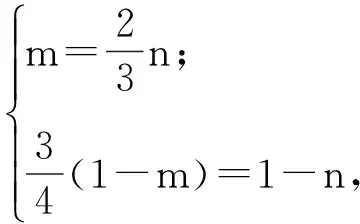
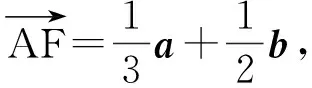
证明由题意得

f′(x)=x2+2ax+b.

设f(x)的2个极值点为x1,x2，则x1,x2∈[1,2]，且x1,x2是方程f(x)=0的2个根,于是

f′(x)=(x-x1)(x-x2),

得

即

由1≤x1≤2,得

同理可得

于是

即

0≤a+b≤2.

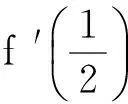
2 建立不等式

如果在考虑一个量时，一方面得到了精确的结果，而另一方面采用了估计(放缩)，或者2个方面都采用了估计(一放大、一缩小)，那就产生了不等式．

例3对于某些正整数n，存在A1,A2,…,An为集合{1,2,…,n}的n个不同的子集，满足下列条件：对任意不大于n的正整数i,j，①i∉Ai，且每个Ai中至少含3个元素；②i∈Aj的充要条件是j∉Ai(其中i≠j)．为了表示这些子集，作n行n列的数表，规定第i行第j列的数为

(1)求该数表中每列至少有多少个1；

(2)用n表示该数表中1的个数，证明：n≥7；

(3)请构造出集合{1,2,3,4,5,6,7}的7个不同子集A1,A2,…,A7，使得A1,A2,…,A7满足题设条件(写出1种答案即可)．

解(1)由①知数表中每列至少有3个1．

(3)可以构造A1={2,3,4},A2={3,4,5},A3={4,5,6},A4={5,6,7},A5={6,7,1},A6={7,1,2},A7={1,2,3}.

例4已知f(x)是定义在R上的函数，且对任意x∈R，满足f(x+4)-f(x)≤2x+3，f(x+20)-f(x)≥10x+95，且f(0)=0，则f(24)=________.

解f(24)=f(0)+[f(4)-f(0)]+[f(8)-

f(4)]+…+[f(24)-f(20)]≤

2×(0+4+…+20)+3×6=

f(24)=f(4)+[f(24)-f(4)]≥f(4)+135,

同理可得

f(20)≤95,f(20)≥95,

因此

f(20)=95.

由于f(20)≤95是将5个同向不等式相加而得到的，因此这5个同向不等式同时取等号，故f(4)-f(0)=3,即f(4)=3,从而f(24)≥138.

综上所述

f(24)=138.

评注本题2次利用了算两次思想，均实现了以不等促相等．

例5已知等差数列{an}的首项为a，公差为b，等比数列{bn}的首项为b，公比为a，其中a,b都是大于1的正整数，且a1b2,对于任意的n∈N*，使得am+3=bn成立，则an=

( )

A.2n+1 B．3n-1

C．5n-3 D.6n-2

解由a3>b2得

由a1

a

(2)

因为a,b都是大于1的正整数，将式(1)的2边都除以ab，得

由式(2)得

(4)

由式(3)，式(4)得

即

a<3.

又由a>1，得

a=2.

等式am+3=bn可化为

2+(m-1)b+3=b·2n-1,

即

b·(2n-1-m+1)=5,

因此b是5的约数，故b=5.综合可得

an=2+(n-1)·5=5n-3.

故选C．

3 归谬

在解决某些存在型探索性问题(或反证法证明命题)时，首先假设满足条件(或假设结论不成立)，考虑某个量的性质，从2个不同的角度，也会得到2个不同的关系，而这2个关系是互相矛盾的，从而说明不存在(或假设错误)．

(1)若函数f(x)是定义域上的单调函数，求实数a的最小值.

(2)在函数f(x)的图像上是否存在2个不同的点A(x1,y1),B(x2,y2)，线段AB的中点的横坐标为x0，直线AB的斜率为k，有k=f′(x0)成立？若存在，请求出x0的值；若不存在，请说明理由．

a≥1.

综上所述，a≥1,a的最小值为1．

(2)假设存在，不妨设0

从而

若k=f′(x0),则

即

(5)

可得u(t)在0

u(t)

式(5)不成立，与假设矛盾,于是

k≠f′(x0).

因此，满足条件的x0不存在．

以上例举了利用“算两次”思想建立方程(等式)、建立不等式、归谬，“算两次”思想还有其他方面的应用，限于篇幅，本文不再赘述．下面的问题供有兴趣的读者练习．

4 精题集萃

图2

(1)求圆G的半径r;

(2)过点M(0，1)作圆G的2条切线交椭圆于点E，F， 证明：直线EF与圆G相切．

(2009年江西省数学高考文科试题)

2．已知函数f(x)=x3-(k2-k+1)x2+5x-2，g(x)=k2x2+kx+1，其中k∈R．

(1)设函数p(x)=f(x)+g(x)，若p(x)在区间(0,3)上不单调，求k的取值范围.

(2009年浙江省数学高考理科试题)

参考答案

2．(1)k∈(-5,-2)；(2)存在，且k=5.

3．提示：由柯西不等式，得

由x+y+z=3,得

从而

得

xyz≥1.

由3个正数的平均不等式，得

即

xyz≤1,

因此，xyz=1,故x=y=z=1.

[1] 单墫．解题研究[M]．上海：上海教育出版社，2007.