基于复变函数方法的水下隧道围岩弹性分析

蔚立元，陈晓鹏，韩立军，王迎超

(1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221008；2.中国矿业大学 力学与建筑工程学院，江苏 徐州 221116；3.中国水电顾问集团 成都勘测设计研究院，成都 610072)

1 引 言

近现代以来交通需求大大增加，江河湖海等水体成了社会进一步发展的制约和瓶颈，人类便利用轮渡、桥梁和隧道等手段进行跨越。最近几十年来，水下隧道由于其独有的特点得到了迅猛发展，逐渐成为与桥梁并举的跨越方式[1－2]。

一般而言，隧道围岩是复杂多变的地质体，但是，通过固结灌浆等人工改良，使得其中的结构面闭合，岩土体完整性有保障后，围岩可视为均质、连续、各向同性介质[3]。覆盖层厚度是水下隧道设计施工中的重要参数和关键指标，许多学者进行了相关研究[4－6]，一般认为其合理值不超过2倍洞径，应属于有地面荷载(上覆水体)作用的浅埋隧道，这样水下隧道围岩应力场、位移场的求解就可以简化为含圆孔半平面体在水平边界上受任意分布荷载的弹性力学问题，并可用解析方法求解。

与深埋隧道相比，浅埋隧道由于受到地表边界和地面荷载的影响，其力学分析在数学处理上历来存在较大的困难[7]。Jeffery[8]和Mindlin[9－10]曾采用双极坐标法进行求解，地面载荷对于应力场的影响在他们的解答中得到了考虑，但是这种方法没有给出位移场分布，而且不适用于隧道非常接近地表的情况。Bobet[11]和Chow[12]在诸多严格假定条件下，基于弹性力学的连续和位移谐调条件，研究了饱和围岩中衬砌隧道的应力场和位移场。Verruijt等[13－16]提出了合理的映射函数，采用复变函数方法，分别研究了第二类边界条件、不考虑岩土体自重情形下，无衬砌浅埋隧道变形导致的地表变形问题，以及考虑岩土体自重情况下，由于隧道构造浮力效应所导致的地表变形问题。王立忠等[17]应用Verruijt提供的基本解法，求得隧道周边给定位移条件下的位移场和应力场，分析了不同埋深、泊松比对位移的影响以及不同埋深对应力场的影响。

上述浅埋隧道的复变函数方法研究中，都是在洞周位移或应力边界条件下进行分析的，由水下隧道抽象而来的“含圆孔半平面体在水平边界上受任意分布荷载”问题尚无文献报导。本文将借助Verruijt提供的共形映射函数，采用复变函数方法对该问题进行求解。

2 问题的描述

水下隧道，或推广为地面荷载下浅埋隧道的围岩分析，可视为任意分布荷载q(z)作用下，边界附近含圆形孔洞的半平面体的弹性分析，在直角坐标系(z平面)下的构形如图1所示。图中，圆形隧道半径为 r0；圆心与地表相距 h；覆盖层厚度为 d；半径与圆心深度之比r0/h为一个重要的几何参数，围岩 区域(即 x 轴以下的圆外区域)标记为R。

根据Muskhelishvili的复变函数方法[18]，应力和位移分量(平面应变条件)可用在区域R内处处解析的复位势φ1(z)、ψ1(z)来表示，见式（1）。

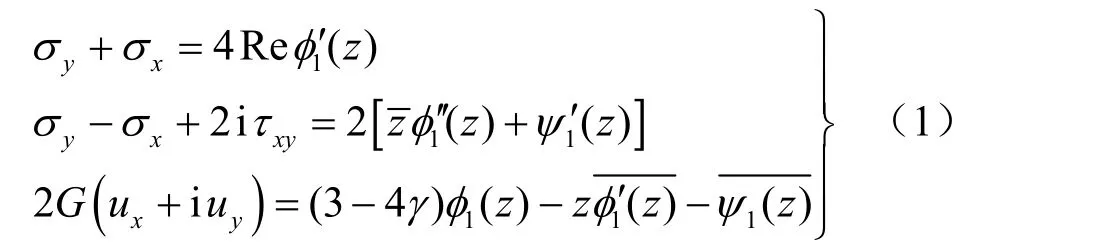
式中：σx、σy、τxy、ux、uy分别为平面问题的应力分量和位移分量为剪切模量；G为剪切模量；γ为泊松比。借助应力边界条件的复变函数式（2），本问题的两个应力边界可表示为式（5）、（6）。

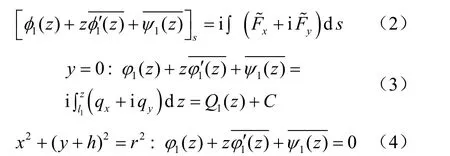
3 共形映射

如图1所示水下隧道的几何构形可以概化为含圆孔半平面体。通过保角映射可把物理平面 z 内的区域 R 变换为像平面ζ内的圆环域[13]。

分式线性映射具有保角性、保形性、保圆性(直线看成是圆的特例)和保对称性，定义式为

式中：a、b、c、d为不全为 0 的待定常数。3个独立条件便能确定一个分式线性映射[19]。如果要求将z 平面上的点 A(0，0)，B(∞，0)，C(0，-d)映射为ζ平面上的对应点 A’(-1，0)，B’(1，0)，C’(-α，0)，则得共形映射函数见式（6），其中，α为由r0/h 确定的参数，见式（7）。z 平面上的R区域映射为ζ平面的单位圆环域r，见图2。容易验证，圆|ζ|=1对应于直线 y=0，而圆|ζ|= α 对应于圆 x2+(y+h)2=若α→0，则r0/h→0，即隧道半径较小，对应于深埋隧道；若α→1，则隧道半径接近于圆心埋深，对应于浅埋隧道。

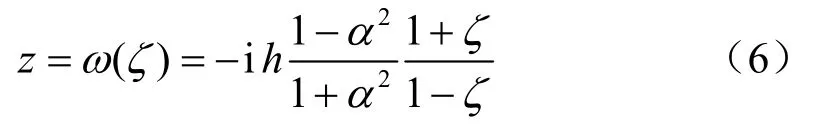
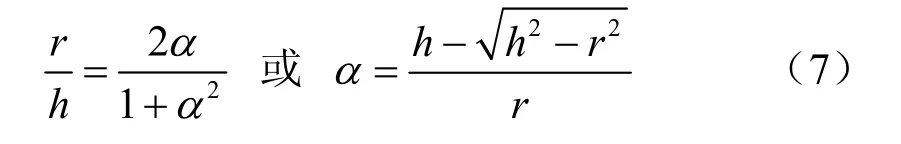
由于复位势φ1(z)、ψ1(z)在区域R内解析，共形映射函数ω(ζ)在圆环域r内解析，由复变函数理论可知ζ平面上的复位势φ(ζ)、ψ(ζ)在该圆环域上也处处解析，这意味着它们可用Laurent级数展开：

式中：系数ak、bk、ck、dk由边界条件确定。

图2 保角映射后的区域Fig.2 The region after conformal mapping

4 边界条件

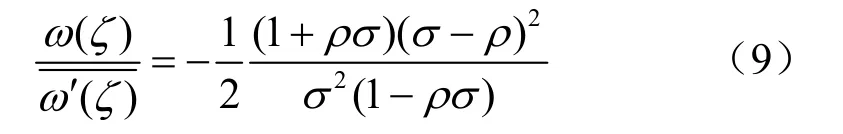
本问题是圆周边界，其表达式比较简单，而对于复杂的孔洞问题，该因子可能异常复杂以致问题难以求解。

4.1 地表边界条件

地表受分布荷载q(z)作用，借助式（3），像平面ζ上的地表边界条件表示为

当地表分布荷载的函数形式确定后，Q(ζ)一般可展开成Fourier级数。水下隧道地表边界y=0，即z=x上作用着均布荷载q(z)=qx+i qy，当作用范围为[l1，l2]时，式（3）右端的积分可表示为

在像平面ζ中，该边界ρ=1，故ζ=ρσ=σ=exp(i)θ，式（12）转换为

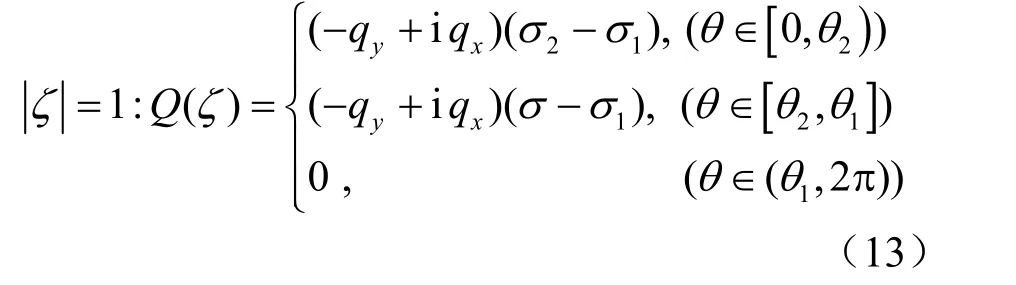
可见，Q(ζ)为周期为2π的周期函数，且满足Dirichlet收敛条件，故可展开成Fourier级数：

将式（8）、（11）、（14）代入式（10），然后，令等号两边σ的同次幂相等，整理可得式（16）。可见，系数ck、dk可用ak、bk显式表示。现在问题的关键在于系数ak、bk的确定，而它们可以通过洞周边界条件求得。

4.2 洞周边界条件

由式（4），洞周的自由边界在ζ平面上表示为

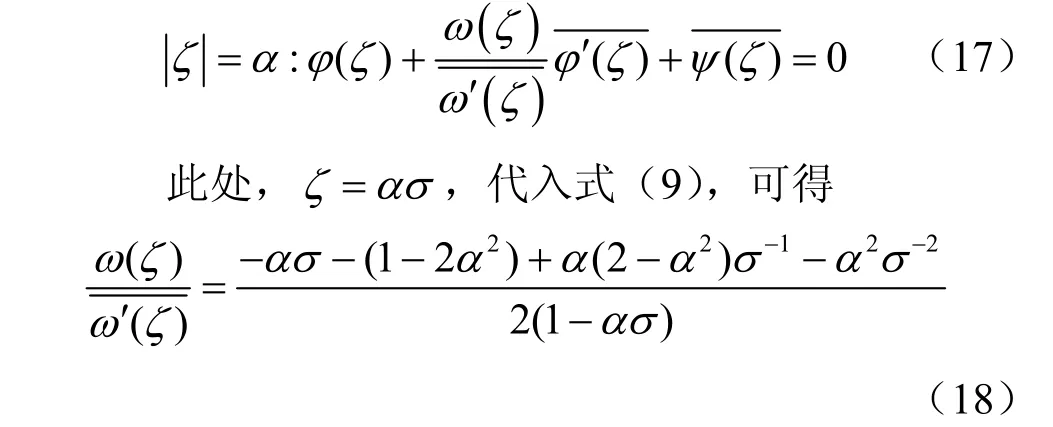
将式（8）、（18）代入式（17），得到一个关于系数ak、bk、ck、dk的相当复杂的方程组，再利用式（16），就能整理出系数ak、bk的迭代方程组：

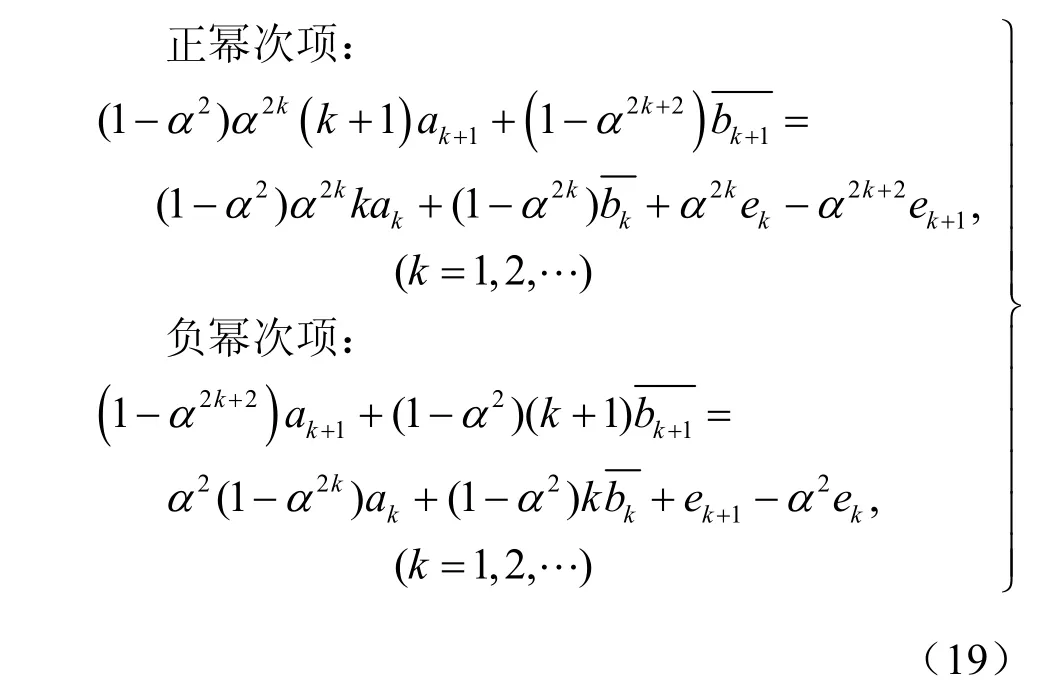
如果已知ak，bk，通过求解一个二元一次方程组，就能得到系数ak+1，bk+1。初始解a1，b1可以借助对σ0、σ1项的整理得到：

式（20）中的系数a0不产生应力，对应于刚体位移，可视为0，这样可求得

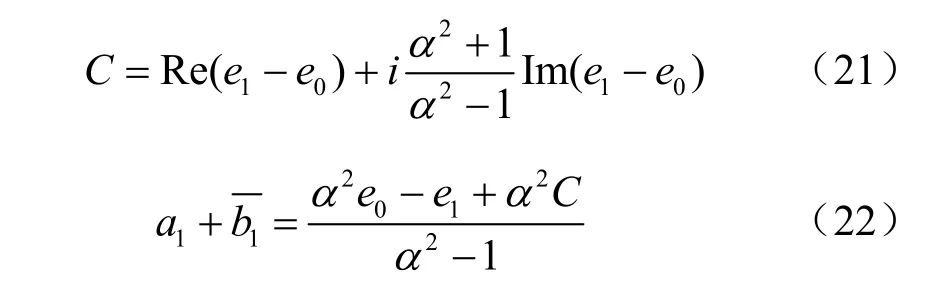
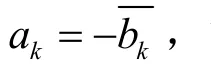
5 返回物理平面求解

为便于表示，可令

然后，由式（6）可得

对于物理平面中的任一点z=x+iy，都可以由式（24）求出对应的像平面中的点ζ，将其代入式（6）、（8），再利用像平面上的应力、位移表达式（25），就能得到该点的应力和位移分量。

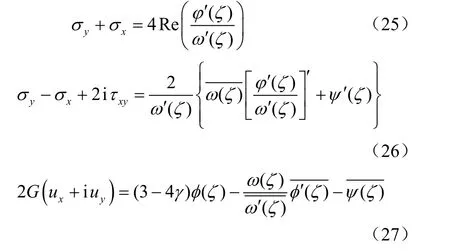
6 程序流程和算例

6.1 程序流程

按照上述方法，能够计算上覆水体荷载作用下水下隧道围岩的应力和位移，但计算过程相当繁琐。通过编写程序，借助计算机求解是一个方便的途径。编写fortran程序的流程见图3（判断ak是否趋近于非0极限时，推荐从l=1 000开始，每增加1 000判断一次）。

6.2 水下隧道算例

对于水下隧道而言，由于上覆水体的黏性对岩土体表面的影响可略去不计[20]，故荷载为其产生的均布法向荷载，且作用范围非常广泛，但在实际运算中选择 10倍洞跨左右，就可以满足工程精度要求。在本例中，隧道半径为5 m，覆盖层厚20 m，上覆水体深30 m，具体参数可见表1。

6.3 正确性验证

图3 计算程序流程图Fig.3 The flow chart of the calculation program

表1 水下圆形隧道计算参数Table 1 Calculation preferences for an underwater tunnel

为了验证本方法的正确性，应用权威有限元分析软件Ansys对上述案例进行分析。由于近似解析方法的求解域是含圆孔半平面体，数值计算只能选择尽量大的区域(210 m×100 m，见图4)来逼近，计算采用平面应变模式。人工边界条件如下：上表面是应力边界，而侧边和下表面为法向约束的位移边界条件。其他条件和参数与章节6.2中相同。

图4 水下隧道计算模型Fig.4 Calculation model for the underwater tunnel

由计算得出得两个应力分量，利用式（25）可求出主应力。

覆盖层中和洞周边界上的6个关键点的两种方法计算结果的对比见表 2，一对数据中前面的是数值计算结果，后面的是近似解析方法结果，其中负值表示压应力，ux、uy分别为水平位移和竖直位移。由表可见，近似解析法和有限元方法的结果基本相同，说明本方法是可靠的。

表2 关键点计算结果对比Table 2 The calculation results comparison of key points

6.4 应力分析

主应力1σ的极值分别是拱顶附近的-8.14 kPa和右拱脚附近的-0.20 MPa，主应力2σ的极值分别是拱顶附近的-0.08 MPa和左右边墙中部的-0.80 MPa。水平方向隧道中线左右70 m，垂直方向地表以下80 m范围内的围岩主应力等值线图如图5所示。由图可见，中线左右2倍洞跨、底板以下两倍洞跨到地表范围内围岩应力集中现象明显，覆盖层尤其应给予重点关注。

6.5 位移结果

由于问题的几何形状、约束情况、以及所受荷载在水平方向上的对称性，隧道中线的水平位移ux为 0，围岩的水平位移都可以精确计算。然而，半平面体垂直方向上不受约束，所以垂直位移（即沉陷）uy不能确定，这时只能求得相对沉陷。取隧道中线上的点 J(0，-100)为基点，围岩中任一点对于基点 J的相对沉陷等于该点的沉陷减去 J点的沉陷。

水下隧道覆盖层中不同深度位置的沉降槽如图6所示，图7为拱顶以上中线各点沉陷值随深度的变化曲线，变形前后的隧道轮廓对比见图8(为便于表达，洞周点位移是实际值的1 000倍)，围岩位移的等值线如图9所示。

综合各图，水下隧道围岩的位移有以下特点：(1) 隧道中线两侧 2倍洞跨范围内，沉降槽比较陡峭，然后逐渐平滑，最后趋近于水平。(2) 从深度方向来看，地层沉陷结果显示出明显的分层传递性，即沉降变形由地表到拱顶传递，变化逐渐减弱，沉降值由拱顶到地表递增，在近原点处取得最大值2.37mm，但沉降槽随着深度增加越来越陡峭。(3)隧道的水平收敛非常小，可以忽略不计，洞周点垂直位移随距地表距离增加而逐渐减小，从 2.09 mm(拱顶)依次变为 1.72 mm(边墙中部)，1.36 mm(底板)，隧道断面面积缩小为原面积的 91.7%。(4)中线两侧2倍洞跨、底板以下一倍洞跨到地表范围内，围岩位移受隧道开挖影响明显，边墙外侧岩土体水平位移由向洞内收敛急剧变成向远方移动，设计施工中应特别注意。

图5 围岩主应力等值线图（单位：102 kPa）Fig.5 Isoline maps of principal stresses(unit: 102 kPa)

图8 隧道变形后轮廓Fig.8 Contour of a underwater tunnle after deformation

图9 围岩位移分量等值线图Fig.9 Isoline maps of displacement components

7 结 语

把水下隧道围岩的弹性分析从力学角度理想化为“含圆孔半平面体在地表边界上受任意分布荷载”问题，利用分式线性映射的特点，确定含圆孔半平面体变换为像平面上单位圆环域的共形映射函数。基于 Verruijt提供的基本方法，推导该问题的一般解法，给出均布荷载边界条件在像平面上的级数形式。采用Fortain语言，编写了计算程序，给出特定水下隧道算例的围岩应力、位移结果，并分析了其受力变形特点，并指出设计施工中应该注意的地方。

本文从理论上完善了半无限平面含括一个孔洞在地表分布荷载边界条件下的求解过程，对水下隧道的具体设计施工具有一定的指导意义。

[1] 王梦恕.水下交通隧道发展现状与技术难题[J].岩石力学与工程学报, 2008, 27(11): 2161－2172.WANG Meng-shu.Current developments and technical issues of underwater traffic tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2008, 27(11): 2161－2172.

[2] 王梦恕.台湾海峡海底铁路隧道建设方案[J].隧道建设, 2008, 28(5): 517－526.WANG Meng-shu.Construction scheme of Taiwan Strait subsea railway tunnel[J].Tunnel Construction, 2008,28(5): 517－526.

[3] 薛守义, 刘汉东.岩体工程学科性质透视[M].郑州:黄河水利出版社, 2002.

[4] 李术才, 李树忱, 徐帮树, 等.海底隧道最小岩石覆盖厚度确定方法研究[J].岩石力学与工程学报, 2007,26(11): 2289－2295.LI Shu-cai, LI Shu-chen, XU Bang-shu, et al.Study on determination method for minimum rock cover of subsea tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2289－2295.

[5] 张顶立, 李兵, 房倩, 等.基于风险系数的海底隧道纵断面确定方法[J].岩石力学与工程学报, 2009, 28(1): 9－19.ZHANG Ding-li, LI Bing, FANG Qian, et al.Method for determining longitudinal section of subsea tunnel based on risk coefficient[J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 9－19.

[6] 蔚立元, 徐帮树, 李术才, 等.确定水下隧道覆盖层厚度的经验公式及其应用[J].地下空间与工程学报, 2011,7(3): 497－503.YU Li-yuan, XU Bang-shu, LI Shu-cai, et al.Empirical formulas for deciding overburden thickness of underwater tunnel and relevant applications[J].Chinese Journal ofUnderground Space and Engineering, 2011, 7(3): 497－503.

[7] SAGASETA C.Analysis of undrained soil deformation due to ground loss[J].Geotechnique 1987, 37(4): 301－326.

[8] JEFFERY G B.Plane stress and plane strain in bipolar coordinates[J].Transactions of the Royal Society of London,(Series A), 1920, 221: 265－293.

[9] MINDLIN R D.Stress distribution around a tunnel[J].Transactions of the ASCE, 1940, 1117－1153.

[10] MINDLIN R D.Stress distribution around a hole near the edge of a plate under tension[C]//Proceedings of the Society of Experimental Stress Analysis, [S.l.]: [s.n.],1948, 5: 56－57.

[11] BOBET A.Analytical solutions for shallow tunnels in saturated ground[J].ASCE Journal Engineering Mechanics, 2001, 127: 1258－1266.

[12] CHOU W I, BOBET A.Predictions of ground deformations in shallow tunnels in clay[J].Tunnelling and Underground Space Technology 2002; 17: 3－19.

[13] VERRUIJT A, BOOKER J R.Surface settlements due to deformation of a tunnel in an elastic half plane[J].Geotechnique, 1996, 46: 753－756.

[14] VERRUIJT A.Deformations of an elastic half plane with a circular cavity[J].International Journal of Solids and Structures 1998; 35(21): 2795－2804.

[15] VERRUIJT A.A complex variable solution for a deforming circular tunnel in an elastic half-plane[J].International Journal for Numerical and Analytical Methods in Geomechanics 1997, 21: 77－89.

[16] STRACK O E, VERRUIJT A.A complex variable solution for a deforming buoyant tunnel in a heavy elastic half-plane[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2002; 26: 1235－1252.

[17] 王立忠, 吕学金.复变函数分析盾构隧道施工引起的地基变形[J].岩土工程学报, 2007, 29(3): 319－327.WANG Li-zhong, LÜ Xue-jin.A complex variable solution for different kinds of oval deformation around circular runnel in an elastic half plane[J].Chinese Journal of Geotechnical Engineering, 2007, 29(3): 319－327.

[18] MUSKHELISHVILI N I.Mathematical theroy of elasticity[M].Leyden: International Publishing, 1954.

[19] 刘建亚.复变函数与积分变换[M].北京: 高等教育出版社, 2005.

[20] 朱镜清, 周建.海底地震动估计的一个流体力学基础[J]地震工程与工程振动, 1991, 11(3): 87－93.ZHU Jing-qing, ZHOU Jian.A fluid mechanics basis for estimating undersea ground motion[J] Earthquake Engineering and Engineering Vibration, 1991, 11(3):87－93.