青藏铁路抛石护坡路基强迫对流特性数值分析

卞晓琳，何 平，吴青柏，施烨辉

（1.清华大学 环境科学与工程系，北京 100084；2.北京交通大学 土建学院隧道及地下工程教育部工程研究中心，北京 100044；3.中国科学院寒区旱区环境与工程研究所 冻土工程国家重点实验室，兰州 730000）

1 引 言

青藏铁路建设中广泛采用了抛石气冷路基、抛石护坡路基等工程措施，该类结构能够自然冷却路基下的冻土层，从而达到减少甚至消除寒区路基融沉的效果[1－2]。抛石可以看作多孔介质，其内部流体的对流换热为多孔介质的传热传质问题。多孔介质中的热质迁移问题是一个较为复杂的强非线性问题，无法求得解析解，通常采用数值方法进行理论分析，如Neto等[3]利用Darcy流，通过数值计算，对抛石路堤的对流传热进行了研究；Ahmed等[4]应用显式差分法，分析了不可压缩流体通过多孔介质的强迫对流效果和相应的热质运输过程；米隆等[5]基于多孔介质流体动力性理论，利用有限元方法，对青藏铁路抛石路堤、抛石护坡降温效果进行了数值计算分析；赖远明等[6]根据多孔介质中流体热对流的连续性方程、动量方程和能量方程，引进流函数和应用伽辽金法，导出了多孔介质对流换热的有限元公式，并对普通道碴路基、抛石护坡路基和抛石路基的温度场进行了分析比较，结果表明普通道碴路基的修建将使路基下冻土的温度升高，使冻土路基出现热不稳定，而抛石路基和抛石护坡路基均能降低冻土路基的温度；姜凡等[7]应用有限体积法，对某块石路基内的温度和速度特性进行数值分析，计算时对块石层分别采用多孔介质模型和“块石”模型，结果表明冬季块石层内空气速度场的形态为一个逆时针的涡包，夏季则为顺时针涡包，采用“块石”模型计算得到路基内的整体温度略低于多孔介质模型的结果，速度则大于多孔介质模型计算结果。

目前关于抛石护坡路基自然对流方面的数值模拟研究较多，而强通风条件下抛石护坡路基内强迫对流特性方面的研究则较少。为此，本文基于多孔介质中流体热对流的连续性方程、非达西流动量方程和能量方程，对强通风条件下青藏铁路典型抛石护坡路基内温度场和流速场的分布形态进行理论分析，结合现场试验结果，对抛石护坡路基的强迫对流特性进行研究。

2 理论背景

将抛石层视为多孔介质，忽略路堤长度方向的不均匀效应，简化为横断面方向的二维各向同性问题。基于以上假设，其内部热对流方式为非稳态的非等温渗流，控制方程为连续性方程、动量方程和能量方程。

连续性方程：

式中：vx、vy分别为空气在 x、y方向上的速度分量。

动量方程：

考虑空气不可压缩且ρa是温度的函数，为了简化分析，使用Boussinesq近似，即只有重力项中的空气密度是可变的，可表示为

式中：β为空气的热膨胀系数；ρ0、T0分别为空气密度和稳定的参考值。

能量方程：

式中：Ca为空气的定压比热；分别为为介质等效体积热容和等效导热系数。

空气区域为流体区，采用如下控制方程（N-S）方程：

连续性方程为

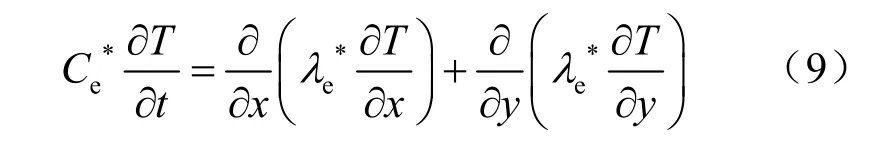
计算中应用显热容法，假设模型中含水介质相变发生在温度区间（Tm±ΔT*）。当建立等效体积热容时，应考虑温度间隔 ΔT*的影响，同时，假设介质在正冻、未冻时的体积热容Cf和Cu以及导热系数λf和λu不取决于温度，因此，简化构造出和的表达式：

式中：L为含水介质单位体积相变潜能。

3 计算模型

3.1 工点概况

本研究以青藏铁路北麓河试验段抛石护坡路基结构为原型。该试验段位于青藏高原可可西里与风火山之间，北麓河盆地南部，地貌形态属北麓河冲洪积高原地貌。区域地势开阔，地形略有起伏，冲沟发育，植被覆盖也较好。该地区属青藏高原干旱气候区，寒冷干旱，空气稀薄。一年内冻结期长达 7～8个月，蒸发量大，年平均气温为-5.2 ℃，最高温为23.2 ℃，最低温为37.7 ℃，年平均降雨量为290.9 mm，相对湿度平均为57%；最大风速为40 m/s，年平均风速为4.10m/s，主导风向为北西。

青藏铁路北麓河试验段为厚层地下冰地段，地下冰分布极为广泛，钻探资料表明，该地段全范围内均有含土冰层分布，体积含冰量大于50%，多为悬浮状构造。地层上部为粉、细砂夹碎块石，下部活动层范围主要为棕红色粉质黏土，上限附近有1.0～3.0 m厚的含土冰层，下部以棕红色全风化泥岩为主，局部有砂岩夹层。

3.2 计算模型

选取青藏铁路北麓河试验段抛石护坡路基结构为计算断面。抛石护坡厚度为80 cm，抛石粒径为8～15 cm，路基填筑高度为3.7 m，地层材料包括抛石护坡、路堤填土、活动层以及多年冻土层。路基上方区域为流体区域，考虑路基左右护坡通风条件不同，路堤计算边界条件并不对称，故本研究中仍以整体路基结构为计算对象。

图1为抛石护坡路基的计算模型。计算域以路基坡脚向外延伸各 30 m，天然地表上下各延伸30 m。图中，区域①为路基砂砾料填土；区域②为细砂活动层；区域③、④分别为黏土活动层；区域⑤为黏土；区域⑥为强风化泥岩；区域⑦为抛石护坡；区域⑧为流体区；A～N为区域边界。

图1 计算模型（单位：m）Fig.1 Calculation model (unit: m)

3.3 材料参数

研究工点各介质的物理参数见表 1。表中，L为介质的相变潜能；抛石层渗透率k=1.58×10-6；惯性阻力系数（非达西流的Beta因子）B=1 650.24 m-1，其他符号意义同前。

表1 路基结构中各介质的物理参数Table 1 Thermal parameters of media in embankments

3.4 边界条件

考虑全球气候变暖的影响，根据文献[8]，取青藏铁路未来50年年平均气温上升2.6 ℃，设初始年平均气温为-4.0 ℃，由于路基模型上表面温度变化不仅与环境空气有关，且受太阳辐射等复杂因素的综合作用，故根据吸附面理论及北麓河气象站的长期现场观测资料，对计算域的热边界条件进行如下假定。

气温变化规律：

式中：t为时间变量（h），当t=0对应的初始时间为 7月20日；假定通过JK边的热流密度为q =0.06 W/m2，边界AMJ和DNK视为绝热。

由于抛石护坡中空气与外界连通，其内部温度场和速度场直接受到外界通风条件的影响，所以抛石层与空气的接触面EF和GH设置为流体可通过界面，在这些界面上施加温度荷载的同时，外界风可通过这些界面穿过抛石层。此外，为了使计算与实际更为接近，计算中将风速边界施加于距离坡脚30 m处的AB边界上，即取模型边界AB为风速的入口边界，气温按式（11）变化。

对北麓河气象站观测资料分析，计算工点地面以上10.85 m高度标准风速变化规律可近似为

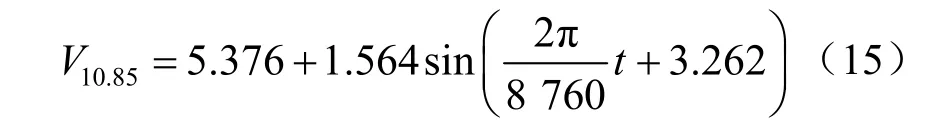
根据“综合幂次律”理论[9]，考虑到试验段的主导风向为NW，故入口边界AB的风速可近似表达为

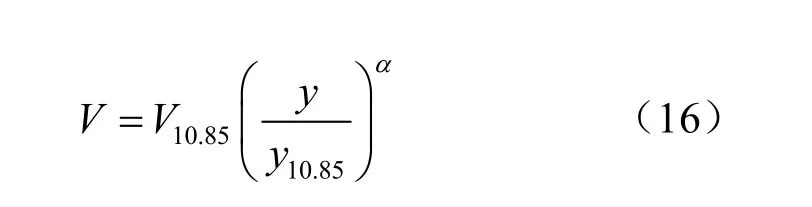
式中：V为任意高度风速；V10.85为10.85 m高度的标准风速；y、y10.85分别为V、V10.85对应的高度；α值由试验获得，本次计算取0.16。

根据北麓河气象站的实际观测资料，热初始条件按式（12），不考虑升温的天然地表温度方程作为区域②～⑥的上边界条件进行反复多年计算，逐时段求解，直至得到稳定的温度场为止；此时年变化层以下稳定场基本保持稳定，年变化层以上相同位置的温度值在同一时间逐年相同，本模型取5月31日温度场作为该区计算的温度初始条件。速度初始条件取不考虑能量方程式（4）和式（8），定温条件下以式（16）为边界条件，计算得到的5月31日稳定速度场作为计算流体区速度初始条件。

4 计算结果与分析

4.1 模型的合理性验证

以青藏铁路北麓河试验段抛石护坡路基结构断面为研究对象，对本文所建立的计算模型的合理性进行验证。根据现场观测资料，对计算域的热边界条件作如下假定：

该试验段于2004年9月施工完毕，计算中以路基在2004年10月5日实测地温数据作为计算的热初始边界，以式（18）为速度边界计算得到的相应时刻温度速度场作为初始速度条件。

图2、3为青藏铁路北麓河试验段抛石护坡路基结构断面在夏季8月30日和冬季12月27日温度场模拟与实测结果对比图。本文中温度场实测资料由中国科学院寒区旱区环境与工程研究所提供，从图中可以看出，模拟所得温度场与实测值分布规律基本一致，路堤的修筑使下部冻土上限有所抬升，存在地温升高的现象。图4为青藏铁路北麓河试验段抛石护坡路基结构断面在环境风速最大时刻的速度分布对比示意图。从图中可以看出，左侧抛石护坡中空气在外界大气风场的强迫作用下，基本沿抛石护坡斜向上运动，靠近护坡外表面的空气流速大，护坡下部速度较小，模拟空气流速在 1.4×10-3～13.1 m/s之间，实测空气流速在1.6×10-3～14.6 m/s之间，模拟结果与实测结果基本一致。

图2 抛石护坡路基夏季温度场（单位：℃）Fig.2 Temperature distributions of the crushed-rock slope embankment in summer (unit: ℃)

图3 抛石护坡路基冬季温度场（单位：℃）Fig.3 Temperature distributions of the crushed-rock slope embankment in winter (unit: ℃)

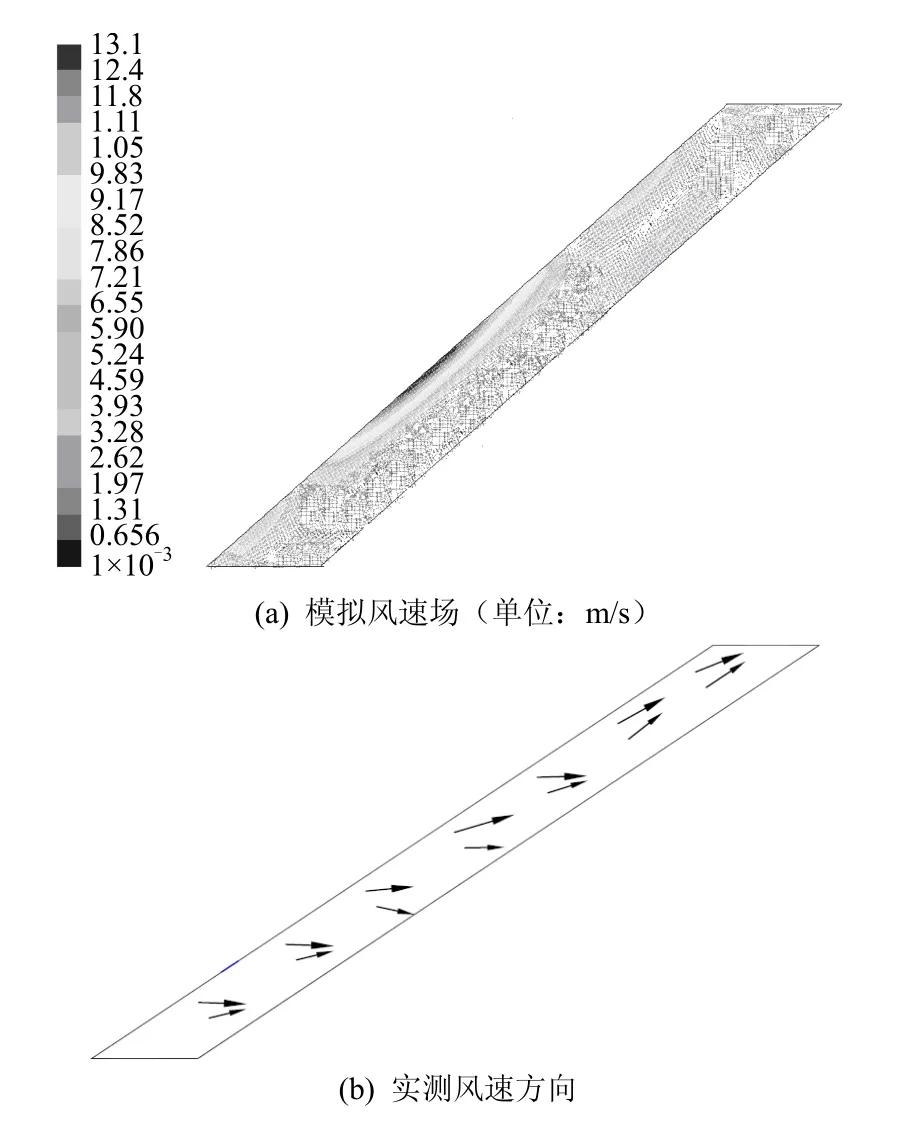
图4 抛石护坡路基断面左侧护坡内速度场Fig.4 Velocity distribution of the pore air in crushed-rock side slope

从上述结果中也可以看出，模拟温度场和实测温度场的分布形态略有差异，整体而言，本文建立的计算模型及参数的获取方法是合理的，能够反映出抛石护坡路基在强通风条件下的主要特性。

4.2 温度场分析

图5为抛石护坡路基修筑完成2年后的温度分布。由图中可以看出，抛石层主要以导热为主，越远离环境，则冻土层内的温度变化受环境的影响越小。此外，由于强风的方向为从左向右，所以路堤左侧护坡附近空气与填土的换热能力高于右侧，故左侧填土接近大气来流方向的温度变化较右侧快，左侧等温线的斜率略高于右侧。由图 5(a)可见，路基在7月15日最高温度升至10 ℃以上，最低温度为-2.5 ℃，路基中部以下产生了一个-2.5 ℃的低温冻土核，其温度低于周围土体约-1.5 ℃。天然地表下，冻土的最大融深坐标y=-1.5 m，而路基中线处y=0.7 m，表明抛石护坡路基的修筑，使多年冻土上限提升了约 2.2 m。由图 5(b)可见，路基在次年冬季1月15日已全部完成回冻，但天然地表以下局部仍有0 ℃等温线存在，表明抛石护坡路基下部土体回冻速度较天然地表下部土体更快。

图6为抛石护坡路基修筑完成50年后的温度分布。由图中曲线看出，随着全球气候变暖，冻土的整体温度有所升高，多年冻土上限（0 ℃等温线）有所下降。由图6(a)可见，夏季7月15日最高气温升至13 ℃，最低气温为-2 ℃，路基中线以下土体的内部产生了“似眼球状”融化夹层，由图6(b)可见，尽管冬季外界温度较低，而“似眼球状”融化夹层仍然存在，且范围有所增大，表明该融化夹层贯穿于抛石护坡路基修筑完成50年的整个冻融区，不利于路基的稳定。

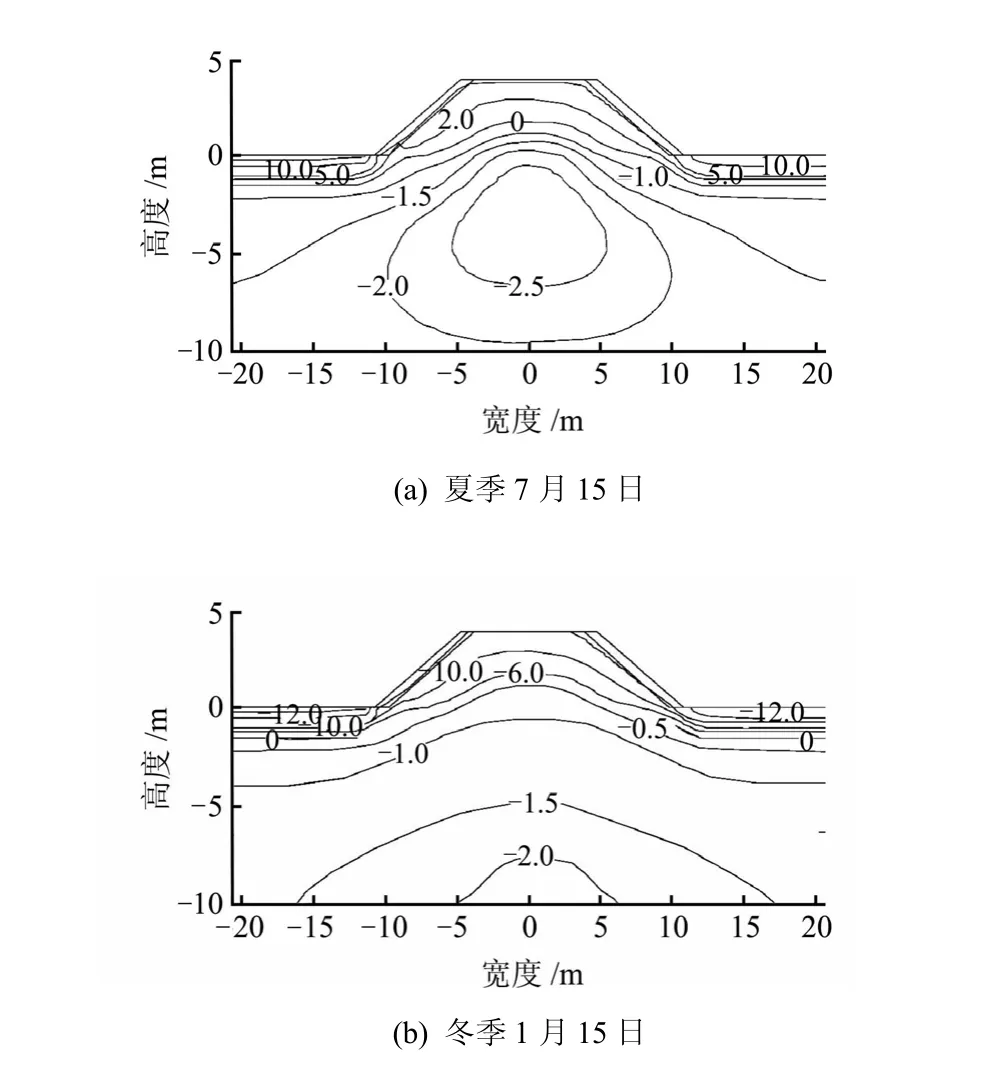
图5 修筑完成后第二年温度分布（单位：℃）Fig.5 Temperature distributions of the crushed-rock slope embankment after 2 years of the construction (unit：℃)

图6 修筑完成后第50年温度分布（单位：℃）Fig.6 Temperature distributions of the crushed-rock slope embankment after 50 years of the construction (unit: ℃)

4.3 速度场分析

强通风条件下模型中的空气运动主要以强迫对流为主，故不同时刻空气运动规律差别不大，本文仅以环境风速最大时刻的速度场为例对抛石护坡路基的速度场进行分析。

图7为本次计算环境风速最大时刻抛石护坡路基的速度分布示意图，由于抛石层内外空气运动差异较大，所有图中矢量只表示流体的运动方向，不代表大小。由图可见，计算域的风向自左向右，故流通区矢量的方向以向右为主，迎风抛石护坡层中空气运动方向大致为沿护坡斜向上，背风抛石护坡层中空气运动方向以从下到上运动为主。图8为左侧抛石护坡层细部的速度分布图。由图可以看出，抛石层中空气运动较为零乱，空气在抛石缝隙处绕流抛石，整体而言，抛石孔隙中空气运动形式为“绕流”。抛石层表面空气速度最大，内部较小，空气速度分布区间为 1.24×10-3～12.8 m/s，与现场试验测得的风速区间基本一致。

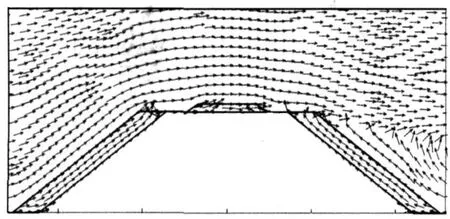
图7 抛石护坡路基速度场分布Fig.7 Velocity vectors at maximum wind

图8 左侧抛石护坡路基速度场分布（细部）（单位：m/s）Fig.8 Velocity distribution of the pore air in crushed-rock side slope at maximum wind（unit: m/s）

5 结 论

（1）强通风条件下，抛石护坡路基对保护多年冻土具有积极作用。路基修筑完成2年的温度计算结果表明，抛石护坡路基的存在使夏季多年冻土上限提高了约 2.2 m，冬季抛石护坡路基下部土体回冻速度较天然地表下部土体更快。

（2）降温作用主要集中在护坡附近有限范围之内，对路基中部的降温作用相对较弱，抛石护坡对冻土路基本体的保护作用有限。从长期降温效果来看，由于全球气候变暖的影响，强通风条件下抛石护坡路基中线以下土体的内部可能产生“似眼球状”融化夹层，不利于路基的稳定。

（3）迎风抛石护坡层中空气运动方向大致为沿护坡斜向上，背风抛石护坡层中空气运动方向以从下到上运动为主，抛石层内空气的运动形式为“绕流”，抛石层表面空气速度最大，内部较小，空气速度分布区间为 1.24×10-3～12.8 m/s，与现场试验测得的风速区间基本一致。

[1] SUN Zhi-zhong, MA Wei, LI Dong-qing.In situ test on cooling effectiveness of air convection embankment with crushed rock slope protection in permafrost regions[J].Journal of Cold Regions Engineering, 2005, 19(2): 38－51.

[2] 吴青柏, 赵世运, 马巍, 等.青藏铁路块石路基结构的冷却效果监测分析[J].岩土工程学报, 2005, 27(12):1386－1390.WU Qing-bai, ZHAO Shi-yun, MA Wei, et al.Monitoring and analysis of cooling effect of block-stone embankment for Qinghai-Tibet railway[J].Chinese Journal of Geotechnical Engineering, 2005, 27(12): 1386－1390.

[3] NETO H L, QUARESMA J N, COTTA R M.Natural convection in three-dimensional porous cavities: Integral transform method[J].International Journal of Heat andMass Transfer, 2002, 45(14): 3013－3022.

[4] AHMED N, SUNDADA D K.Nonlinear flow in porous media[J].Journal of the Hydraulic Division, ASCE,1969, 95: 1847－1857.

[5] 米隆, 赖远明, 张克华.冻土通风路基温度场的三维非线性分析[J].冰川冻土, 2002, 24(6): 765－769.MI Long, LAI Yuan-ming, ZHANG Ke-hua.3D nonlininear analyses for temperature field of ventilative embankment in cold regions[J].Journal of Glaciolgy and Geocryology, 2002, 24(6): 765－769.

[6] 赖远明, 张鲁新, 徐伟泽.青藏铁路抛石路基的温度特性研究[J].冰川冻土, 2003, 25(6): 291－296.LAI Yuan-ming, ZHANG Lu-xin, XU Wei-ze.Temperature features of broken rock mass embankment in the Qinghai-Tibetan railway[J].Journal of Glaciolgy and Geocryology, 2003, 25(6): 291－296.

[7] 姜凡, 刘石, 王海刚, 等.冻土碎（块）石路堤传热与对流特性数值计算分析[J].中国科学（D辑）, 2003,33(增刊): 133－144.JIANG Fan, LIU Shi, WANG Hai-gang, et al.Numerical analysis on the heat transfer and convection characteristics of broken rock mass embankment[J].Science in China (Series D), 2003, 33(Supp.): 133－144.

[8] 秦大河.中国西部环境演变评估综合报告[M].北京:科学出版社, 2002.

[9] 贝尔.多孔介质流体动力学[M].北京: 中国建筑工业出版社, 1983.