粒径对剪胀特性的影响及其细观机理探讨

王开来 苏 强

(中煤平朔集团有限公司东露天矿，山西朔州 036000)

0 引言

剪胀性作为土区别于其他材料的一个本质特征，自其被发现以来［1］，就引起了广大学者的浓厚兴趣，关于土的剪胀性的研究成果也不断涌现。人们逐渐认识砂土等颗粒材料的塑性体积变形来源于两个方面的原因:应力的变化和剪切变形的产生［2］。应力的变化将导致颗粒的相互靠近与破碎;剪切变形导致颗粒的相互攀爬与翻滚，把由剪切变形诱发的塑性体积应变增量称为Reynolds剪胀［3，4］。Reynolds剪胀是由剪切变形导致的真正的剪胀，与剪切变形密切相关。

随着研究的深入，人们发现砂土等材料微观颗粒大小，位置随机分布的不均匀性，连接方式与排列方式等导致在受力过程中形成诸多强度迥异的力链［5］，贯穿于颗粒物质内，在宏观上则表现出剪胀等力学性质，为此须从细观角度开展研究。

基于离散元的颗粒流软件的出现，克服了传统连续介质力学模型的宏观连续性假设，可以从细观层面上对砂土的工程特性进行数值模拟。国内外很多学者在此做了大量的工作，文献［6］～［8］研究了细观参数与宏观力学响应的关系等。迟明杰等［9］提出的剪胀机理解释了砂土所具有的复杂现象，但是针对细观参数与Reynolds剪胀关系的研究较少。本文首先建立仅考虑剪切变形影响的简化模型，分析颗粒粒径这一微观参数与体积应变的关系，并利用PFC2D软件进行数值模拟实验，进一步验证与讨论粒径对Reynolds剪胀的影响。

1 Reynolds剪胀与粒径无关机理推导

实际土体压缩变形很复杂，伴随着有颗粒相互翻越抬起，胶结的破坏，颗粒的压碎等现象的发生。简化模型需对土体细观结构的复杂性进行大量简化，进而在细观层面来探讨其规律性。简化过程如下:设有粒径分别为r1和r2的均匀颗粒组(本文采用的为单位厚度的圆盘)，图1对应于颗粒处于疏松状态时(此时颗粒已充分接触，但相对于图2来说，仍为疏松状态)的简图，图2对应于颗粒处于剪缩之后的紧密状态时的简图。当两组粒径不同的r1和r2都经历从图1到图2的过程时可进行如下分析(假设颗粒单元为刚性体，变形过程颗粒不破碎，相互不重叠)。

1．1 单位体积下的颗粒数

在单位体积下，对不同的r1和r2，在初始状态1时，由于配位数为4，每个孔隙由4个圆盘分得，而每个圆盘周围有4个孔隙，所以每个圆盘应占有体积(包括孔隙)v1，v2可求出。

因为图1状态时，单个孔隙所占体积:

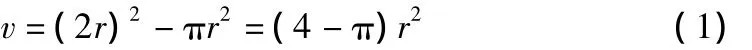
其中，r为圆盘半径。

所以有:

其中，r1为圆盘1的半径;v1为对应于r1的圆盘所应占有的体积。

其中，r2为圆盘2的半径;v2为对应于r2的圆盘所应占有的体积。

那么由式(2)和式(3)求得单位体积下对应r1的颗粒数n1=1/4r21，对应r2的颗粒数n2=1/4r22。

图1 疏松状态

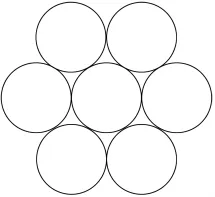
图2 紧密状态

1．2 从疏松到紧密体积应变εv的变化

对r1，图1状态对应的孔隙比为:

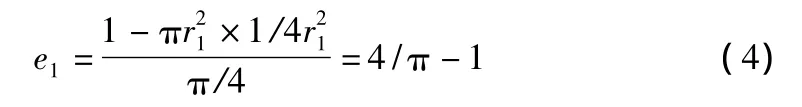
在图2状态时，单个孔隙所占体积:

又由于配位数为6，每个孔隙由3个圆盘分得，每个圆盘周围有6个孔隙，所以每个圆盘应占有2个孔隙，所以压缩之后孔隙比为:

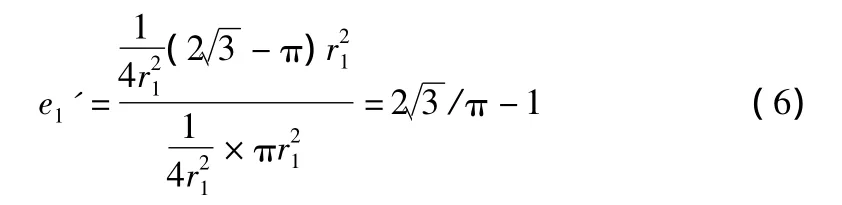
那么过程中孔隙比的变化Δe1可由式(4)和式(6)求得:

由Δe1导致体积应变:

同理，由式(7)和式(8)可以求得对r2也有该过程孔隙比的变化:

其中，e2，e2'分别为半径为r2的圆盘在图1状态和图2状态的孔隙比。

同样可求得对应于r2的体积应变:

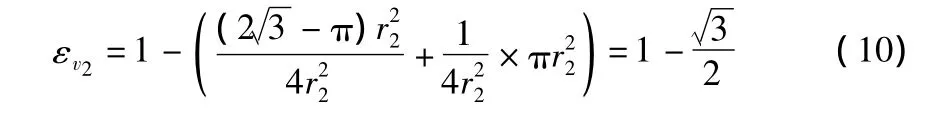
从推导过程可以看出，在压缩过程中，粒径的大小与孔隙比的变化和体积应变无关。而这种简化模型的压缩过程其实就是反映的纯剪切变形的过程，所以也可以说该简化模型的剪切变形导致的体积应变即Reynolds剪胀，与粒径无关。

2 PFC2D双轴实验对结论的验证

2．1 PFC2D基本理论

二维颗粒流程序PFC2D是通过离散单元方法来模拟圆形颗粒介质的运动及其相互作用。这种方法是研究颗粒介质特性的一种工具，它采用数值方法将物体分为有代表性的数百个颗粒单元。利用颗粒模型理解单元的力学特性后，用连续介质的方法来求解包含复杂变形方式的真实问题。

PFC2D能模拟任意大小圆形粒子集合体的动态力学行为，在整个计算过程中交替应用力—位移定律和牛顿运动定律，颗粒与颗粒以及颗粒与墙之间通过接触联系起来，接触性质由下列单元组成:

1)线性弹簧或简化的Hertz-Mindlin准则;2)库仑滑块;3)粘结类型。

此外PFC2D在模拟过程中还作了如下假设:1)颗粒单元为刚性体。2)接触发生在很小的范围内。3)颗粒单元为圆盘形。

这些假设与前面建立的模型假设基本类似，所以不必另外附设条件，可直接用来模拟。作为实际问题的模拟应先进行微观参数的标定，确定微观参数与宏观力学特性的关系，找到能模拟实际问题的比较合适的微观参数值。因本文做的是定性分析，并没有进行标定的过程。

2．2 PFC2D模型实验

实验发现如果采用相同的粒径rmax/rmin≈1，实验结果失真。这可能是由于在模拟的过程中，相同的粒径会形成格子架的结构［10］，故采用粒径比 rmax/rmin=1．20以及 rmax/rmin=2的颗粒“样品”，通过改变rmin的大小，形成不同粒径大小的颗粒组来说明相同的问题。

PFC中实验模型的生成先是按指定的颗粒粒径及分布规律，在指定的区域生成较松散的颗粒组，再通过扩大半径法或压缩法等达到指定的孔隙率。本实验采用扩大半径法，主要的控制参数见表1，表1中在粒径比相同的情况下，分别取最小颗粒半径为0．075和0．085来生成“样品”。

表1 砂土PFC模型基本控制参数

因PFC模型试验的假设条件中没有考虑颗粒的破碎，所以图3中体积应变即为Reynolds剪胀部分。

当rmax/rmin=1．2时，颗粒均匀分布，且PFC2D试验采用的是二维圆盘颗粒，与模型假设基本一致，从图3中剪缩部分可以看出，两组粒径“样品”在实验中表现出的体积应变(即Reynolds剪胀部分)基本类似，符合文中1．2的推导结论。

当rmax/rmin=1．2，对比两组粒径的孔隙比，发现在孔隙降低的过程中(即剪缩过程)，两者基本重合，孔隙增大时，相差较大。这也与文中1．2推导结论基本吻合(见图4)。

当rmax/rmin=2时，颗粒均匀分布，与模型假设偏离较大，曲线剪缩部分重合度不如rmax/rmin=1．2时的好。但剪胀部分重合反而比前者好(见图5)。这可能是由于粒径比大，级配更好，颗粒结构重组更快，粒径比的影响就降低了。

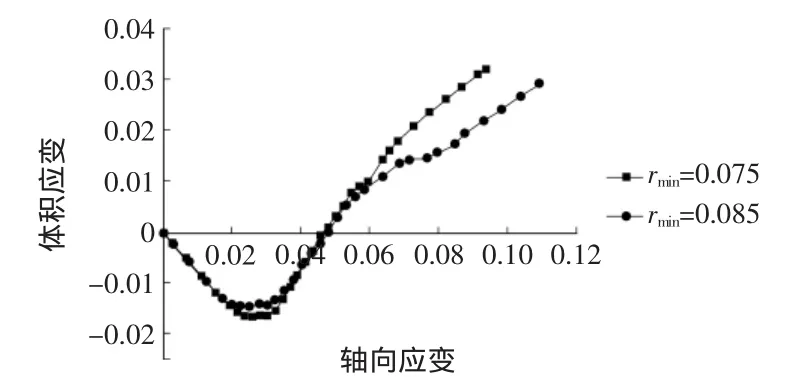
图3 r max/r min=1.2时的体变—轴向变形曲线

图4 r max/r min=1.2时的孔隙比—步数曲线

图5 r max/r m in=2.0时的体变—轴向变形曲线

2．3 数值实验结果讨论

从数值模拟实验结果可以看出，当rmax/rmin较小时，两组“样品”的体积应变曲线基本重合，其压缩过程产生的体积应变(即Reynold，剪胀部分)与粒径的大小基本无关，验证了文中1．2的推导结论。当粒径比较大时，两组“样品”的体积应变曲线重合度不如前者，说明粒径比的大小对实验结果还是存在一定影响的。

3 结语

本文首先建立了一个仅考虑剪切变形剪胀模型，推导出颗粒的大小不影响孔隙比变化值和体积应变值的大小，再用PFC2D软件数值模拟了这一变形过程，从实验结果指出粒径对Reynolds剪胀无关的结论。当然本文的简化模型仍存在缺陷，如没有考虑颗粒的破碎，颗粒的形状过于简化，颗粒的自身变形没有考虑等。

［1］Reynolds，O．On the dilatancy ofmedia composed of rigid particles in contact．With experimental illustration［J］．Philosophical Magazine，1985(20):469-482．

［2］张建民．砂土的可逆性与不可逆性剪胀规律［J］．岩土工程学报，2000，22(1):158-161．

［3］郑颖人，孔 亮．岩土塑性力学［M］．北京:中国建筑工业出版社，2010．

［4］Collins IF，Muhunthan B，Tai A T T．The concept of‘Reynol-ds-Taylor state’and themechanics of sands［J］．Geotechnique，2007，57(5):437-447．

［5］孙其诚，王光谦．颗粒物质力学导论［M］．北京:科学出版社，2009．

［6］周 健，迟 永．土的工程力学性质的颗粒流模拟［J］．固体力学学报，2004，25(4):377-382．

［7］周 健，迟 永．砂土力学性质的细观模拟［J］．岩土力学，2003，24(6):901-906．

［8］曾 远，周 健．砂土的细观参数对宏观特性的影响研究［J］．地下空间与工程学报，2008，3(4):499-503．

［9］迟明杰，赵成刚，李小军．砂土剪胀机理的研究［J］．土木工程学报，2009，42(3):99-104．

［10］S．v．Baars．Discrete element analysis of granuar materials［D］．Delft:Delft University of Technologly，1996．