不同填充及加载路径下劈裂砂岩渗流特性研究
2012-11-05李建林赵宗勇
刘 杰,李建林,赵宗勇,肖 蕾,蔡 健
(三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002)
1 引 言
关于岩体裂隙的渗流研究前人已有诸多成果。在外荷载下岩体渗流规律的试验研究方面,Olsson等[1]从渗流与岩体外加载荷的耦合方面入手,通过试验和理论分析,分析了一定载荷下岩体节理的渗流特性。Lee等[2]研究了在基本和剪切荷载下线性流动在粗糙裂隙中的水力特性。许光祥 等[3]通过多种人工裂隙的试验研究,证明了吻合粗糙裂隙符合次立方定律,而非吻合粗糙裂隙遵循超立方定律。仵彦卿等[4]运用岩石高压三轴加载装置和渗透压加载装置,分析了岩石应力-应变过程中孔隙率、渗透速度、渗流速度、微孔隙直径、渗透率等的变化规律。刘才华等[5]采用人工劈裂贯通裂隙,进行三轴应力下的渗流实验,研究结果表明法向应力、侧向应力以及渗压对裂隙渗透系数有显著的影响。胡昱等[6]通过试验,研究了多轴应力作用下砂砾岩单裂隙渗流规律,成果表明法向应力和侧向应力对裂隙的渗透系数有着明显的影响,共同决定着渗透系数的变化。
在含充填物裂隙渗流研究方面,刘才华等[5]在对人工充填砂裂隙进行剪切实验的基础上,分析了剪应力和法向有效应力作用下裂隙岩石的渗流特性。陈金刚等[7]研究了充填物拉张效应、剪切效应、塑化效应和液化效应对裂隙的渗透性影响。刘杰[8]对含密实原岩充填物的宜昌砂岩裂隙渗流试验研究,研究了加载路径、原岩充填物粒径等因素对渗流量的影响。
在岩样劈裂裂纹的渗流研究方面,胡昱等[6]用劈裂的方法在砂砾岩块上制造裂隙,模拟天然岩体的张性裂隙,成果表明法向应力和侧向应力对裂隙的渗透系数有着明显的影响,共同决定着渗透系数的变化。侯昭飞[9]使用劈裂方法,在粗砂岩岩样上制造裂隙来模拟粗砂岩天然岩体的张性裂隙,对单裂隙岩体在三维应力作用下的渗流规律作了探究。刘才华等[5]在对人工充填砂裂隙进行剪切实验的基础上,提出了剪应力和法向有效应力耦合作用下的渗流公式。
综上,研究取得丰富研究成果,但现有试验中很少系统地研究有填充物条件下,劈裂岩体在加载路径、围压、轴压、填充物厚度、粒径等不同因素影响下的渗流规律。开展这方面研究,可以丰富和完善现有的岩体裂隙渗流理论,同时,这些影响因素在实际工程中常常会导致室内和现场的渗流测试成果出现异常,因此,开展此类研究有一定的工程价值。
2 试验制备及试验仪器
原材料选自于三峡大学云霞小区道路边坡岩石,正交偏光图片见图 1。接触式胶结,岩石中碎屑物主要为石英,白云石,长石,岩屑和黑云母,粒度在0.1~0.3 mm之间,砂粒以0.15~0.2 mm为主,属于中~细粒砂岩。制作直径为 54 mm,110 mm的砂岩劈裂试样岩样,见图 2。本文主要研究砂粒填充条件下加载路径、轴压、围压、填充物颗粒粒径及填充物厚度对渗流速度的影响规律。
前期研究表明,不同砂粒粒度进行填充时,围压σ3= 1.5~5 MPa之间变化的渗流速度随围压的变化趋近于水平线;当σ3>5 MPa时,影响极微小,因此,选取围压范围为0~5 MPa。轴压在研究中为施加的水头,输出的水头由产生轴向水头电机功率决定,电机可提供0.01~0.2 MPa轴向水头。

图1 正交偏光图Fig.1 Orthogonal polarization graph

图2 劈裂后试样Fig.2 Splitting sandstone samples
试验采集岩块经岩石取芯机、切割机取样制样打磨后,经密度测试和回填试验进行初步筛选后,用NM-4A声波测试非金属超声检测仪(见图3)测量波速。

图3 NM-4A声波测试非金属超声检测仪Fig.3 The NM-4A sound wave nonmetal ultrasound detector test
将波速差异 5%内的列为研究试件。所选试件在RMT-150C岩石力学试验系统(见图4)上进行劈裂试验,劈裂后的试件填砂后用 ELE岩石渗透仪(见图5)进行渗流试验。在对劈裂后的砂岩中,填充 3种不同粗细程度的砂:中细砂(平均粒径0.25~0.5 mm)、粗砂(平均粒径0.5~1.0 mm)和混合砂(中细砂与粗砂的等体积混合)。填充砂的制取选用某建筑工地用砂并利用级配筛分筛筛取。

图4 RMT-150C岩石力学试验系统Fig.4 The RMT-150C rock mechanics test system
如图6所示,使劈裂试件的一侧劈裂面水平向上放置,均匀平铺等厚度的砂粒,将另一侧劈裂面覆盖之后再对铺设不均匀或砂粒空缺处进行微调。由于在渗流的过程中砂会随水流带走或滑移,极有可能堵住出水孔口,本试验用细纱布封住进出口两端,防止水流引起的砂料侧漏,如图7所示。

图6 砂料均匀平铺Fig.6 Evenly spreading the sand
3 有填充物试验方案及结果分析
下面依次分析砂粒填充条件下加载路径、轴压、围压、填充物颗粒粒径及填充物厚度对渗流速度的影响规律。
3.1 加力路径与渗流之间的关系
分析中主要考虑了两种加力路径:加载路径1,从小到大固定围压,轴压从小到大变化;加载路径2,在路径1加载完毕后,将围压和轴压均卸载为0后,从小到大固定轴压,围压从小到大变化,保证一定颗粒粒度和填充厚度下研究不同应力条件下的路径走线。应力条件选择为a~l,a:围压0.5 MPa、轴压0.01 MPa;b:围压0.5 MPa、轴压0.03 MPa;c:围压 0.5 MPa、轴压0.05 MPa;d:围压 1.0 MPa、轴压0.01 MPa;e:围压1.0 MPa、轴压0.03 MPa;f:围压1.0 MPa、轴压 0.05 MPa;g:围压 2.0 MPa、轴压0.01 MPa;h:围压2.0 MPa、轴压0.03 MPa;i:围压 2.0 MPa、轴压 0.05 MPa;j:围压 5.0 MPa、轴压0.01 MPa;k:围压5.0 MPa、轴压0.03 MPa;l:围压5.0 MPa、轴压0.05 MPa。
从图8可以看出,在不同填充物一定的应力情况下,加力路径发生变化,渗流速度也发生变化,无论何种粒度的砂填充,路径2对应的渗流速度与路径1对应的数据并不重合。究其原因,不同加卸载路径下试件裂隙面错动和填充砂粒发生平动和转动并不一致,由此会对渗流速度产生影响。粗砂填充下路径2平均流速是路径1的78.84%,中细砂填充下路径2平均流速为路径1的58.87%,混合砂填充下路径2平均流速为路径1的82.06%,均说明路径2的过流通道小于路径1的过流通道。由于3种粒度的填充厚度有一定差异,填充物粒度的影响这里还不能对比分析。
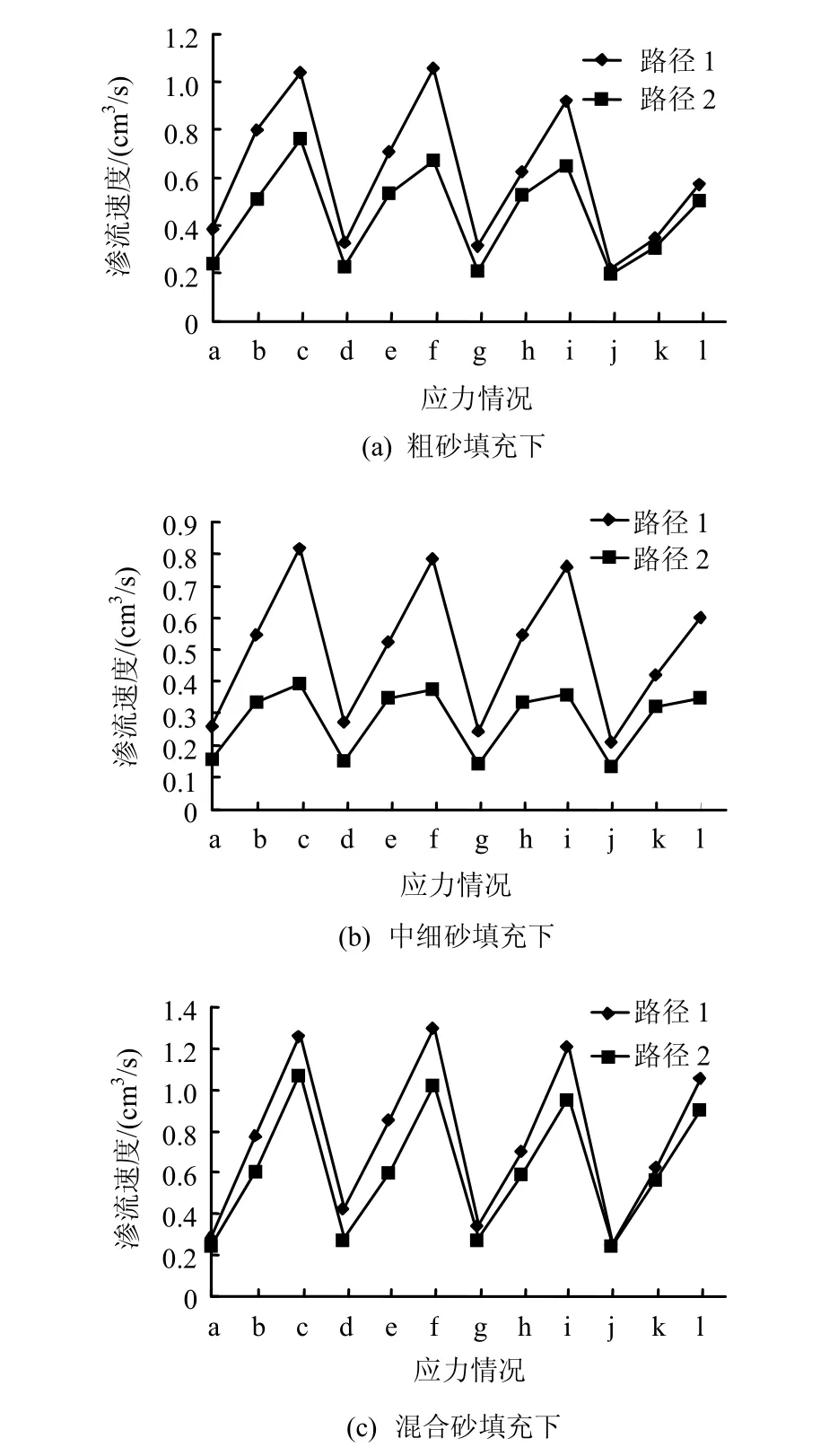
图8 不同路径渗流速度走线图Fig.8 Seepage velocity chart of sandstone filled under different loading paths
3.2 应力与渗流之间的关系
以路径3作为加力路线得出轴压、围压与渗流之间的关系。路径3的加载过程为:从小到大固定围压,轴压从大到小变化。
(1)轴压与渗流之间的关系
围压以 0、0.25、0.5、1、1.5、2、5 MPa分别固定,轴压从0.01 MPa逐渐增加,得到固定围压下轴压与渗流之间的关系,如图9所示。
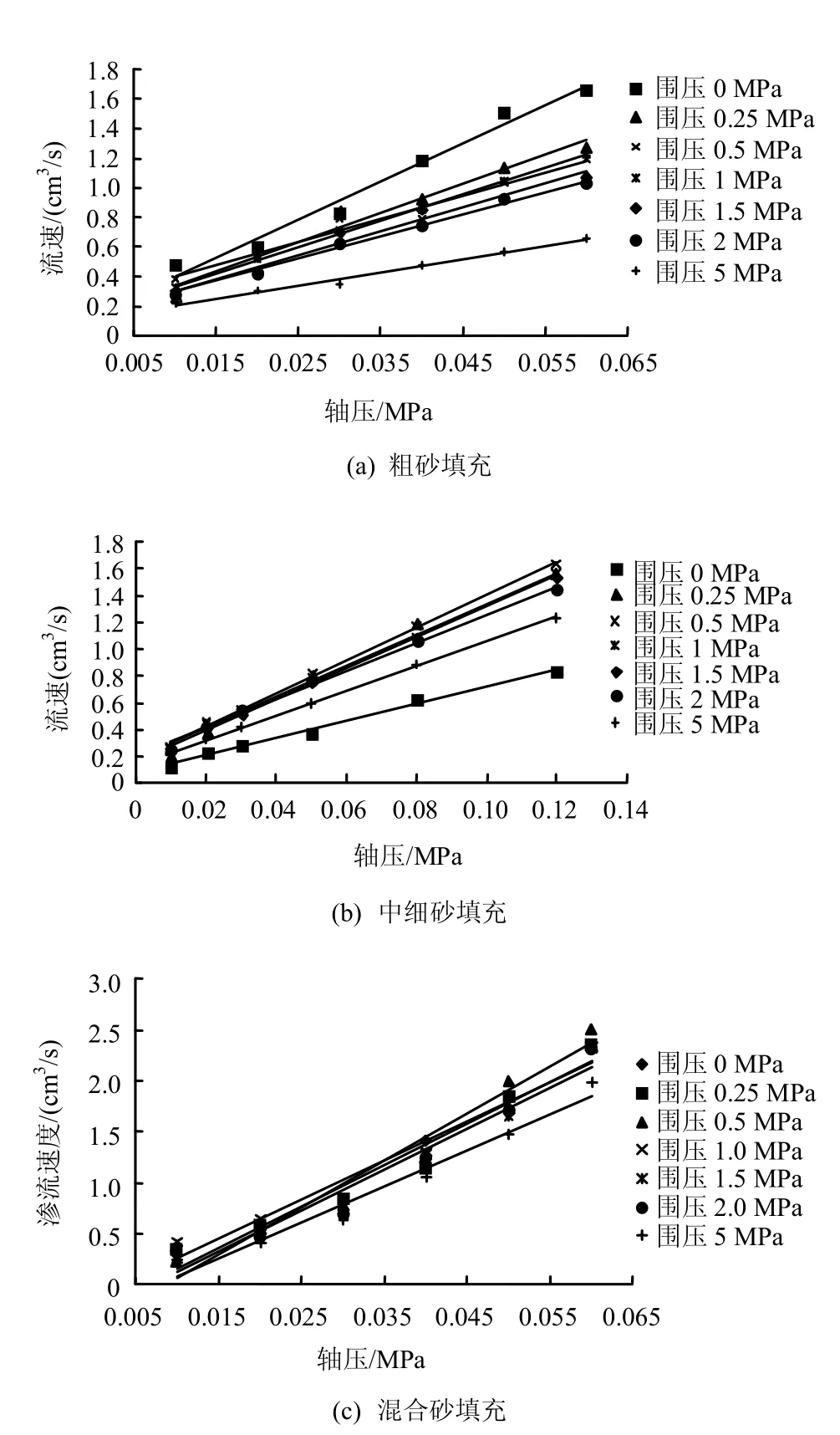
图9 填充不同围压下渗流速度与轴压之间的关系Fig.9 Relationships between seepage velocity and axial compression of sandstone filled under different confining pressure
分析图 9可知,①对于粗砂情况,渗流速度 y与轴压x之间的关系呈线性递增(y = ax+b),拟合线为:围压为0 MPa时,对应的趋势线方程为y =25.814x+0.139,R2= 0.9802;围压为0.25 MPa时,对应的趋势线方程为y = 19.706x+0.1417,R2=0.9731;围压为0.5 MPa时,对应的趋势线方程为y = 15.768x+0.2388,R2= 0.9675;围压为1 MPa时,对应的趋势线方程为y = 17.829x+0.1564,R2=0.9987;围压为1.5 MPa时,对应的趋势线方程为y = 16.066x+0.1472,R2= 0.9684;围压为2 MPa时,对应的趋势线方程为y = 14.817x+0.1554,R2= 0.9922;围压为5 MPa时,对应的趋势线方程为y = 8.935x+0.1172,R2= 0.9869。将围压与系数a和b进行拟合,如图10所示。

图10 粗砂拟合直线系数随围压的变化关系图Fig.10 Straight fitting coefficient changing with the confining pressure in coarse sand filler
通过图9(a)和图10,可以将路径一粗砂填充下围压轴压与渗流之间的关系用复合函数表示:
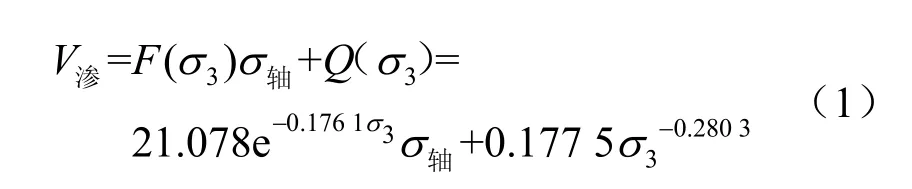
式中:σ轴、σ3分别为轴向应力和围压(MPa);V渗为渗流速度(cm3/s)。
②对于中细砂情况,渗流速度与轴压之间呈线性递增(y = ax+b)关系,拟合线为:围压为0 MPa时,对应的趋势线方程为y = 0.6407x+0.0753,R2=0.9920;围压为0.25 MPa时,对应的趋势线方程为y = 1.2229x+0.145,R2= 0.9885;围压为0.5 MPa时,对应的趋势线方程为y = 1.2269x+0.1788,R2=0.9973;围压为1 MPa时,对应的趋势线方程为y =1.1445x+0.1857,R2= 0.9978;围压为1.5 MPa时,对应的趋势线方程为y = 1.1562x+0.164,R2=0.9983;围压为2 MPa时,对应的趋势线方程为y =1.0482x+0.2017,R2= 0.9935;围压为5 MPa 时,对应的趋势线方程为y = 0.9212x+0.1354,R2=0.9992。各拟合线所对应的斜率随围压的变化如图11所示。
通过图9(b)和图11,可以将路径1中细砂围压轴压与渗流之间的关系用复合函数表示:
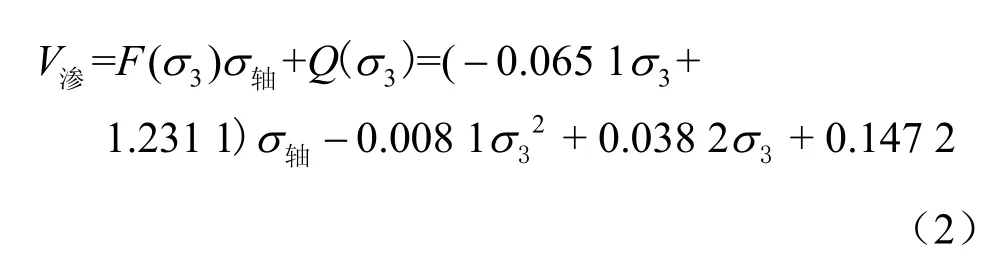

图11 中细砂拟合直线系数随围压的变化关系图Fig.11 Straight fitting coefficient changing with the confining pressure in medium-fine sand filler
③对于混合砂情况,渗流速度与轴压之间的关系呈线性递增(y = ax+b),拟合线为:围压为0 MPa时,拟合方程为y = 41.053x-0.2564,R2= 0.9741;围压为 0.25 MPa时,拟合方程为 y = 40.563x-0.2245,R2= 0.9554;围压为0.5 MPa时,拟合方程为y = 46.127x-0.3867,R2= 0.9644;围压1 MPa时,拟合方程为y = 38.434x-0.1209,R2= 0.9648;围压为1.5 MPa时,拟合方程为y = 41.06x- 0.3314,R2= 0.9583;围压2 MPa时,拟合方程为y = 40.186x-0.2809,R2= 0.9517;围压为5 MPa时,拟合方程为y = 35.277x-0.266,R2= 0.9636。将围压与系数a和b进行拟合,如图12所示。
通过图9(c)和图12可将路径一混合砂填充下围压轴压与渗流之间的关系用复合函数表示:
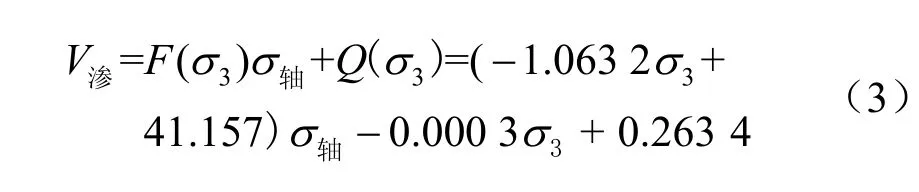
④从各流速与轴压之间的直线拟合关系斜率来看,对粗砂而言,渗流速度与轴压之间拟合的直线斜率与无填充物一样随着围压的增大呈指数递减关系(指数方程为 y = 21.078e-0.1761x);对中细砂,呈直线递减(直线方程为y = -0.0651x+1.2311),对混合砂,呈直线递减(直线方程为y = -1.0632x+41.157),这说明在一定范围内,围压对渗流产生了较大的影响,轴压一定,围压越大,渗流速度越小,但当围压增大到一定程度时,其影响度会逐渐变小。
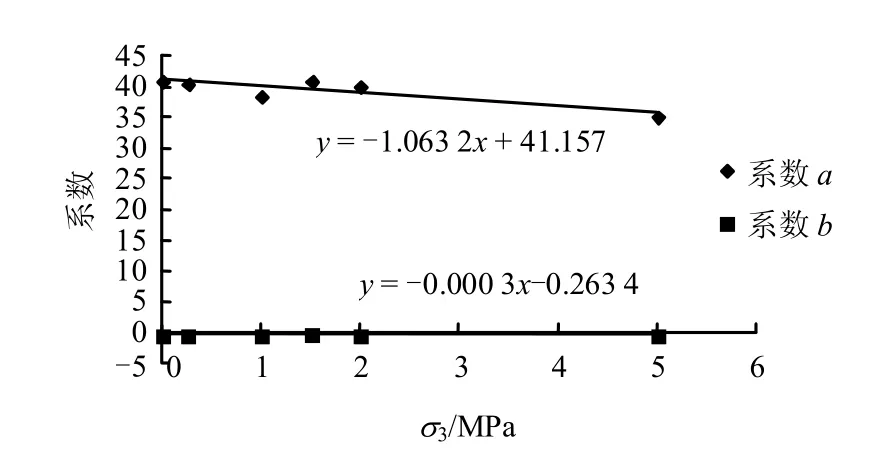
图12 混合砂拟合直线系数随围压的变化关系图Fig.12 Straight fitting coefficient changing with the confining pressure in mixed sand filler
⑤加力路径 1下、三种粒径的砂砂填充下轴压与渗流关系与无填充物一致,均呈线性关系。
(2)围压与渗流之间的关系
粗砂由于渗流速度相对较大,仪器输出功率一定,导致轴压极限荷载较低,试验中轴压以0.01、0.02、0.03、0.04、0.05、0.06 MPa分别固定,中细砂和混合砂以 0.01、0.02、0.03、0.05、0.08、0.12 MPa分别固定,围压从0、0.25、0.5、1、1.5、2、5 MPa逐渐增加,得出的渗流结果数据如图 13所示。从图中可以看出,(1)无填充物下渗流与围压之间呈现的是指数或对数函数递减关系,有填充物下流速与渗流亦呈递减但非指数和对数函数关系。有填充时,σ3≤1.5 MPa时,围压对渗流的影响较大;σ3>1.5 MPa时,围压对渗流的影响极小。分析认为,在低围压下,随着围压的增大过流通道逐渐减小并逐渐压实填充物,导致过流速度减小得较快,但在高围压下,易于压缩的过流通道已压缩完毕,过流通道并不随围压的增大而发生明显的变化;(2)在低轴压下流速与围压的拟合线波动较小,而高轴压下流速与围压的拟合线波动相对较大,这说明围压对渗流的影响在轴压较高时更大。
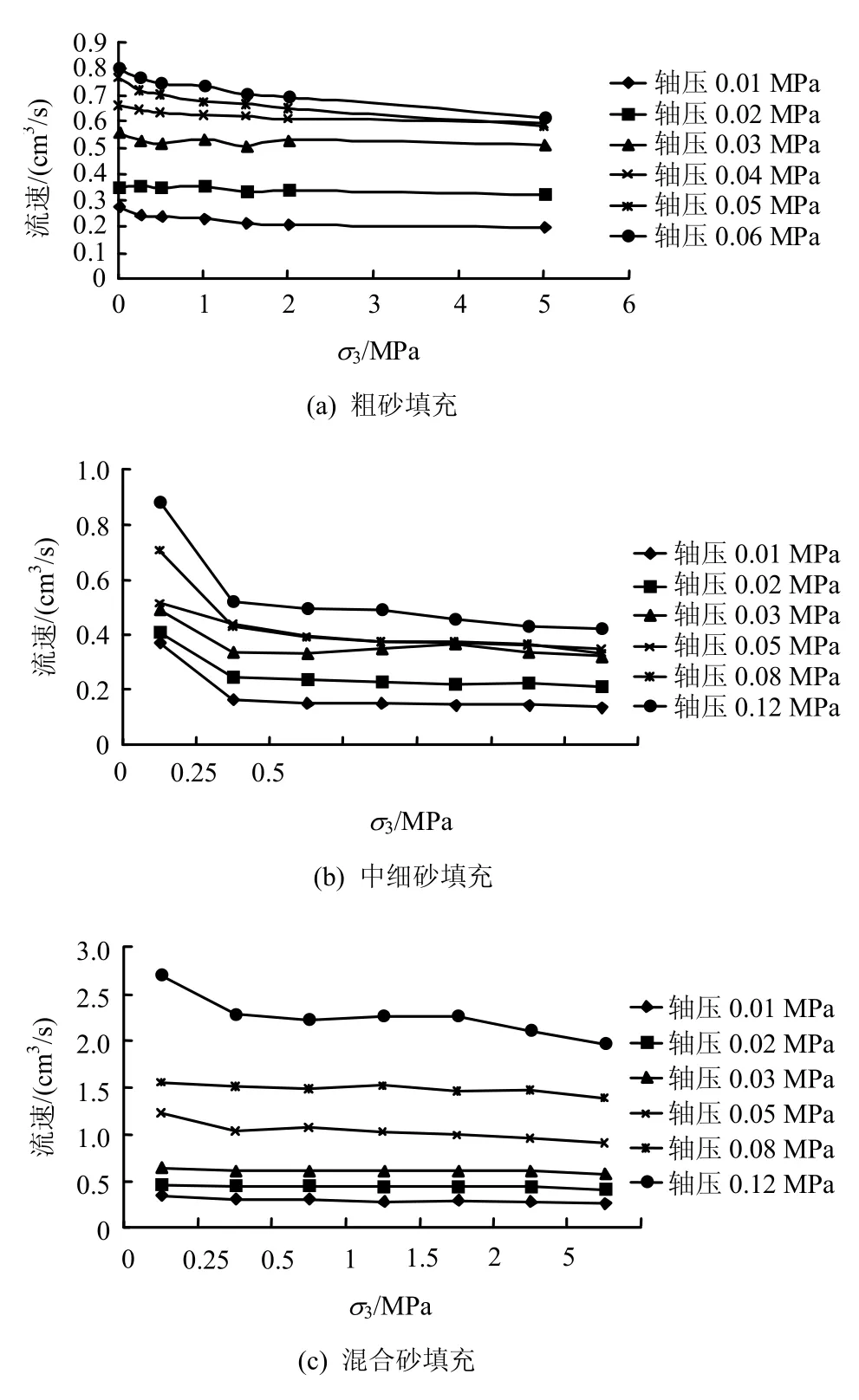
图13 不同轴压下渗流速度与围压之间的关系Fig.13 Relationships between seepage velocity and confining pressure of sandstone filled under different axial pressure
3.3 填砂厚度与渗流之间的关系
对试样两端裂隙填砂厚度、轴向两侧裂隙填砂厚度等 4个厚度进行测量,数据更具代表性,每个厚度量测两次,所有 8个量测数据的平均值取为该试件的填砂厚度。下面分析不同应力下的渗流速度与填砂厚度之间的关系,如图 14所示。分析认为,(1)渗流速度与填砂厚度在一定范围内呈现指数递增关系,各应力情况下对应的拟合函数为:围压 2 MPa、轴压 0.01 MPa,y = 0.0366e1.3602x,R2= 0.8695;围压 2 MPa、轴压 0.03 MPa,y =0.0759e1.4218x,R2= 0.926;围压2 MPa、轴压0.05 MPa,y = 0.0772e1.6395x,R2= 0.8674;围压5 MPa、轴压 0.01 MPa,y = 0.0118e1.9018x,R2= 0.8247;围压5 MPa、轴压0.03 MPa,y = 0.0185e2.0906x,R2= 0.8557;围压 5 MPa、轴压 0.05 MPa,y =0.0246e2.1657x,R2= 0.88。(2)围压一定,轴压越大,导致渗流速度越大,拟合系数越大,指数关系拟合越明显,填砂厚度对渗流的影响越大;轴压一定,围压越小,导致渗流速度越大,填砂厚度对渗流的影响越大。(3)这一指数递增的关系与裂隙开度对渗流的影响极为相似,厚度越大,等效裂隙开度就越大,两者单调递增。
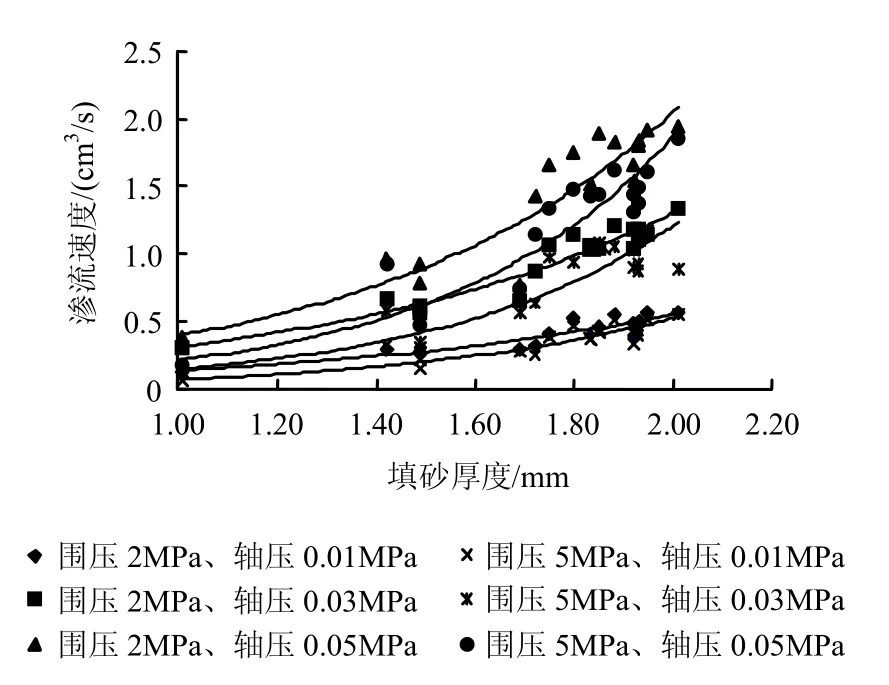
图14 粗砂填充不同应力下填砂厚度与渗流速度关系Fig.14 Relationships between seepage velocity and filler thickness of sandstone filled in coarse sand under different stresses
3.4 填砂粒径与渗流之间的关系
试样2-2-1做了粗、中细、混3种粒度相同填砂厚度下的试验研究。填砂厚1.70 mm,加力路径选择路径1和应力条件选择为,a:围压为0.5 MPa、轴压为0.01 MPa;b:围压为0.5 MPa、轴压为0.03 MPa;c:围压为0.5 MPa、轴压为0.05 MPa;d:围压为1 MPa、轴压为0.01 MPa;e:围压为1 MPa、轴压为0.03 MPa;f:围压为1 MPa、轴压为0.05 MPa;g:围压为2 MPa、轴压为0.01 MPa;h:围压为 2.0 MPa、轴压为 0.03 MPa;i:围压为 2.0 MPa、轴压为0.05 MPa;j:围为压5 MPa、轴压为0.01 MPa;k:围压为5 MPa、轴压为0.03 MPa;l:围压为5 MPa、轴压为0.05 MPa。研究结果如图15所示。从图可见,(1)对于σ3>0.5 MPa的劈裂裂隙而言,一定应力情况中有填充物情况下的渗流速度均大于无填充物下的渗流速度,具体关系为渗流影响度粗砂>混合砂>细砂>无填充物。主要原因为:劈裂试件两裂隙面在围压作用下能较好吻合,过流通道断面极小,而砂粒的填充增大的裂隙开度,砂粒间的过流断面明显大于无填充时的断面,同时,粒度较大的砂粒在同样的填充厚度下将产生较大的过流断面;(2)相同围压条件下,轴压对渗流速度的贡献也受填充物粒度影响,具体关系同上;(3)随着围压的增大,无填充物下的渗流会有明显的降低,但有填充物下的渗流大小影响不太明显,也就是说,有填充物和无填充物在渗流速度上的差异会随着围压的增大而变大。
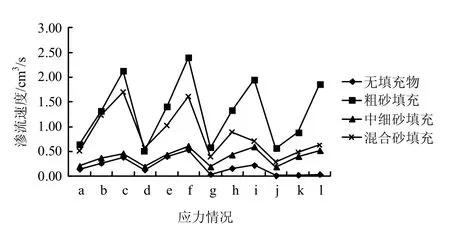
图15 相同填砂厚度不同粒径砂填充不同应力渗流速度图Fig.15 Seepage velocity chart of sandstone in the same filling thickness and different particle diameters under different loading paths
3.5 不同围压下不同填充粒度下所对应的渗流速度对比研究
将填砂粒度均化取值(粗砂粒度为0.750 mm,中细砂粒度为0.375 mm,混合砂粒度为0.625 mm),研究两种应力情况下(围压2 MPa、轴压0.05 MPa和围压5 MPa、轴压0.05 MPa)渗流速度与粒度大小之间的关系,进而研究单位颗粒大小对劈裂后砂岩渗流影响的最大变幅。两种应力不同粒度情况下所对应的渗流速度见图16。从图中可见,随着粒径的增大,渗流速度也随之增大,但并非线性增大的关系,单位粒径对渗流影响的最大变幅有两种:围压2 MPa、轴压0.05 MPa时为9.7072 cm3/s和围压5 MPa、轴压0.05 MPa时为9.7712 cm3/s,无填充时两围压下渗流速度差值最大,进一步说明围压对无填充物的影响大于对有填充物的影响;两条线基本重合,说明较大的围压下围压对渗流的影响不大。
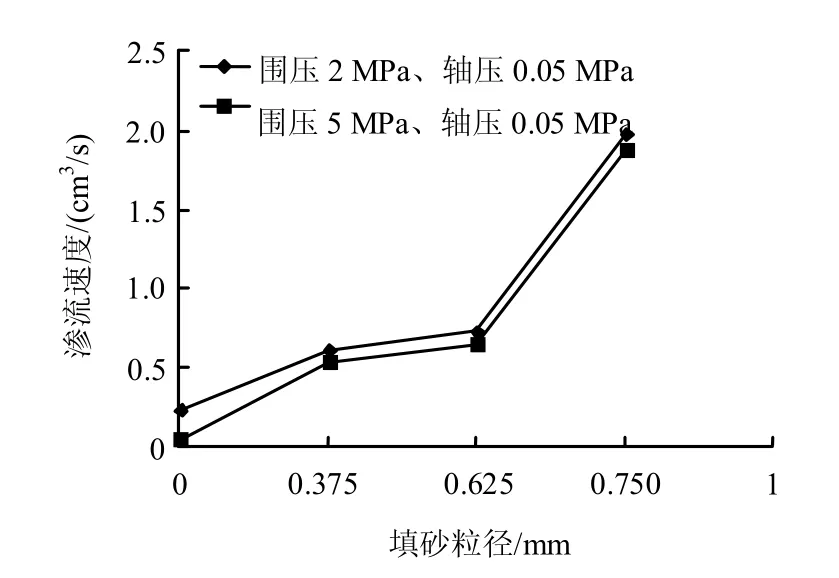
图16 两种应力下渗流速度与填砂粒径大小之间的关系图Fig.16 Relationships between seepage velocity and particle diameter under two kinds of loading paths
4 结 论
(1)在不同填充物一定的应力情况下,加力路径发生变化,渗流速度也发生变化。粗砂填充下,路径2平均流速为路径1的78.84%;中细砂填充下,路径2平均流速为路径1的58.87%;混合砂填充下,路径2平均流速为路径1的82.06%。究其原因,不同加卸载路径下试件裂隙面错动和填充砂粒发生平动和转动不一致,会对渗流速度产生影响。
(2)在加力路径1下,3种粒径的砂砂填充下轴压与渗流关系与无填充物一致,均呈线性关系。
(3)建立了特定条件下轴压围压与渗流速度的定量分析公式。
(4)有围压条件下,无填充物下渗流与围压之间呈现的是指数或对数函数递减关系,有填充物下流速与围压呈线性关系。有填充,且σ3≤1.5 MPa时,围压对渗流的影响较大,σ3>1.5 MPa时,围压对渗流的影响极小。
(5)相同的填充厚度下,随着粒径的增大,渗流速度也随之增大,但并非线性增大的关系。渗流速度与填砂厚度在一定范围内呈现指数关系。
[1]OLSSON R,BARTON N. An improved model for hydro mechanical coupling during shearing of rock joints[J].International Journal of Rock Mechanics and Mining Sciences,2001,38(3): 317-329.
[2]LEE H S,CHO T F. Hydraulic characteristics of rough fractures in linear flow under normal and shear load[J].Rock Mechanics and Rock Engineering,2002,35(4):299-318.
[3]许光祥,张永兴,哈秋舲. 粗糙裂隙渗流的超立方和次立方定律及其试验研究[J]. 水利学报,2003,34(3),74-79.XU Guang-xiang,ZHANG Yong-xing,HA Qiu-ling.Super-cubic and sub-cubic law of rough fracture seepage and its experiments study[J]. Journal of Hydraulic Engineering,2002,34(3): 299-318.
[4]仵彦卿,曹广祝,丁卫华. CT尺度砂岩渗流与应力关系试验研究[J]. 岩石力学与工程学报,2005,23(12): 4203-4209.WU Yan-qing,CAO Guang-zhu,DING Wei-hua.Experimental study on relation between seepage and stress of sandstone in CT scale[J]. Chinese Journal of Rock Mechanics and Engineering,2005,23(12): 4203-4209.
[5]刘才华,陈从新,付少兰. 二维应力作用下岩石单裂隙渗流规律的实验研究[J]. 岩石力学与工程学报,2002,21(8): 1194-1198.LIU Cai-hua,CHEN Cong-xin,FU Shao-lan. Testing study on seepage characteristic of a single rock fracture under two-dimentional stresses[J]. Chinese Journal of Rock Mechanics and Engineering,2002,21(8): 1194-1198.
[6]胡昱,叶源新,刘光廷,等. 多轴应力作用下砂砾岩单裂隙渗流规律试验研究[J]. 地下空间与工程学报,2007,3(6): 1009-1013.HU Yu,YE Yuan-xin,LIU Guang-ting,et al. Experiment research on the laws of seepage in calcirudite rock within single fracture under multiaxial stresses[J]. Chinese Journal of Underground Space and Engineering. 2007,3(6): 1009-1013.
[7]陈金刚,张景飞. 充填物的力学响应对裂隙渗流的影响[J]. 岩土力学,2006,27(4): 577-580.CHEN Jin-gang,ZHANG Jing-fei. Influence of mechanical responses of fillings on fracture seepage[J].Rock and Soil Mechanics,2006,27(4): 577-580.
[8]刘杰,李建林,王瑞红,等. 含密实原岩充填物的宜昌砂岩裂隙渗流试验研究[J]. 岩石力学与工程学报,2010,29(2): 366-374.LIU Jie,LI Jian-lin,WANG Rui-hong,et al. Experimental study of seepage in Yichang fractured sandstone with tight original rock fillings[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(2): 366-374.
[9]侯昭飞,纪洪广,王金安,等. 三维应力作用下砂岩单裂隙渗流规律试验研究[J]. 中国矿业,2011,20(5): 107-110.HOU Zhao-fei,JI Hong-guang,WANG Jin-an,et al.Experiment research on the laws of seepage in sandstone within single fracture under triaxiality stresses[J]. China Mining Magazine,2011,20(5): 107-110.
