基于块体集上限分析的锚板试验模型探讨

余生兵，黄茂松

（1. 同济大学 地下建筑与工程系，上海 200092；2. 同济大学 岩土及地下工程教育部重点实验室，上海 200092）

1 引 言

锚板作为一种基本的抗拔承载力学模型，其抗拔承载力理论分析结果广泛的应用于海洋锚板、抗拔基础、埋置管线上浮和抗拔桩等问题的求解，因此，研究条形锚板的抗拔承载力对于求解这一类抗拔问题有着重要的工程意义。锚板模型试验[1－12]作为一种研究锚板抗拔承载特性的方法，具有其他理论分析方法不可比拟的优点。但是，如果试验模型的设计不够合理，试验结果往往不能正确地反映锚板真实的抗拔承载特性，这对于正确认识锚板的抗拔破坏机制是极为不利的。本文通过块体集上限分析方法，研究了锚板的抗拔承载力和破坏面特性，并将分析结果与文献中已有的模型试验结果进行详细对比，分析斜坡地形条件下现有模型试验中拉杆对于锚板抗拔承载力的影响，并对锚板试验模型的选取提出合理的建议。

2 现有锚板试验模型简述

图1为锚板实验模型示意图。由图1(c)可见，当锚板在拉力作用下移动时，与锚板运动方向相反的一侧土体就处于卸荷回弹状态，该侧土体总是会随锚板运动一段距离，然后再与锚板逐渐脱离。而当锚板埋置在渗透性较差的黏土中时，锚板顶面与底面的超静孔压差会形成一定的吸力，这将提高锚板的抗拔承载力，这就是锚板在拉拔过程中的“吸力”效应，因此，锚板抗拔承载力的发挥实际上与“锚-土”接触面的脱离深度和吸力均密切相关。由于考虑“吸力”效应非常困难，很多学者[2,9,11,13]在考虑“锚-土”接触特性时一般简化为“立即脱离”和“无脱离”两种条件。所谓“立即脱离”，是荷载施加之初锚板即与土体脱离，即完全消除“吸力”的影响，而“无脱离”则假定土体和锚板始终保持接触，即认为“吸力”非常大，“锚-土”接触面由于“吸力”的存在而始终没有脱离。由于“锚-土”接触面的脱离深度和吸力均受较多因素的影响，实际工程中很难确定其大小，而且吸力会随着孔压的消散而逐渐降低。实际工程中通常不考虑吸力对锚板抗拔承载力的影响，即采用“立即脱离”条件，所得结果是偏于安全的。

对于黏性土中的锚板，由于黏性土的渗透系数较小，在拉拔的过程中锚板底面的“吸力”效应非常明显。为了更好地验证现有理论分析的结果，很多学者[3－4]采用了如图1(a)所示的试验模型。该模型为了模拟“立即脱离”模式，一般采取将一个中空并接通大气的有机玻璃盒子放在锚板的下面，以便使锚板底面与大气相通，从而完全消除锚板底面吸力的影响。另一种消除锚板底面“吸力”效应的做法就是直接采用trapdoor模型[14]，即在模型箱底部开洞形成锚板的位置，该试验模型是通过对锚板底面施加推力来模拟锚板的拉拔荷载的，如图1(b)所示。

由图 1(a)和图 1(b)中这两种试验模型的示意图可见，由于锚板底部的土体被移除了，这两种模型试验中锚板的破坏模式均被人为地限制为浅埋破坏模式，而不能自由过渡到深埋破坏模式，因此，这些模型试验的结果中会出现条形锚板抗拔承载力系数大于11.42（深埋条形锚板抗拔承载力系数）的情况。有关块体集上限法对于锚板深埋破坏模式和浅埋破坏模式的分析见文献[15]，限于篇幅，此处不再详述。

另外，一些学者[1,2]采用如图1(c)所示的试验模型来研究条形锚板抗拔承载力，采用这种试验模型对试验过程中锚板底面吸力的控制要求是非常高，在试验过程中，多数情况下是采用控制加载速度来尽可能减少吸力的影响。Rowe[2]在其模型试验中采用中空的拉杆对锚板施加拉力，中空的拉杆可以使锚板底面安装拉杆的地方与大气相通，这在一定程度上可以减少“吸力”效应的影响。对于砂土中的锚板，由于砂土的渗透系数较大，锚板底面的“吸力”效应不明显，模型试验中通常不予考虑，因此，砂土的模型试验多采用图1(c)所示的试验模型。

综上所述，除trapdoor模型可以不采用拉杆来施加拉力荷载外，其他试验模型均需要采用拉杆来施加荷载。

3 块体集上限分析方法

块体集上限分析方法的基本思想是：集成和组合，即将最基本的三角形楔块集成为两个旋转方向各异的旋转块体集（见图2），然后，运用这两个旋转块体集的不同组合来构造所求问题的运动许可速度场，并通过GAPS算法（遗传-模式搜索算法）的优化得到最小上限解。笔者在文献[15]中已经介绍了块体集上限法求解过程。本文所采用的条形锚板运动许可速度场构造方式与文献[15]中分析不排水黏土中条形锚板抗拔承载力所采用的构造方式相同，见图3，即采用两个组合块体集上下累加构成，如图3中①～④均为旋转块体集所示。如图3中运动许可速度场的内能耗散和重力做功见文献[15]，限于篇幅，此处不再详细介绍。

图3 浅埋条形锚板速度场构造示意图Fig.3 Construction sketch of admissible velocity fields for shallow strip anchors

4 块体集上限分析与模型试验对比

4.1 地表水平条件下

地表水平条件下，本文块体集上限分析解与模型试验解的对比如图 4所示。图中，Nc0为不考虑土体重度时锚板的抗拔承载力系数；H为锚板埋深；B为锚板宽度；L为锚板长度。由图4(a)可见，本文上限解与 Das[1]的模型试验对比可以看出，本文块体集上限解与Das的模型试验解吻合较好。图4(b)为本文块体集上限解与 Rowe[2]的模型试验对比。

如图5所示，Rowe的模型试验选用了7个不同尺寸的矩形锚板，并且进行了大量的模型试验，由图可以看出，Rowe的模型试验结果虽然比较离散，但是该模型试验结果的整体趋势与本文块体集上限分析的结果是非常吻合的。

图4 块体集上限解与Rowe模型试验解比较Fig.4 Comparison of pull-out capacities of block set mechanism and laboratory test

4.2 斜坡地形条件下

4.2.1 Khing等模型试验

Khing等[3]通过模型试验研究了饱和黏土中斜坡倾角对水平条形锚板抗拔承载力的影响，在其模型试验中，锚板的宽度B = 7.6 cm，斜坡倾角β分别为 0°、10°、15°、20°、25°，采用的土体重度γ=17.1 kN/m3，不排水抗剪强度cu=10.2 kPa。Khing等的模型试验所得到的结论与文献[15]所得结论相同，即水平条形锚板抗拔承载力随斜坡倾角的增大而减小。

为说明斜坡倾角对锚板抗拔承载力的影响，图5中斜坡倾角分别为 0°和 25°时，块体集上限分析计算结果与Khing等的模型试验结果的对比，图中Nc为考虑土体重度时锚板的抗拔承载力系数。由图中可以看出，在地表水平条件下，本文计算结果与模型试验非常吻合，而在考虑斜坡地形情况时（即斜坡倾角为25°时），Khing等的模型试验结果与本文块体集上限分析的理论预测相差较远。由图5可见，当斜坡倾角由0°增大到 25°时，模型试验结果中锚板抗拔承载力的降低幅度远远小于块体集上限分析的预测。由于该模型试验结果较为离散，一些斜坡倾角为25°时的数据点甚至比斜坡倾角为0°时的结果还要大，这与Khing等的结论相去甚远。笔者认为，由于各种原因该模型试验并不是很成功。

图5 斜坡地形下块体集上限分析结果与Khing的模型试验结果对比Fig.5 Comparison of pull-out capacities of block set mechanism and Khing’s laboratory test results in sloped clayey ground

4.2.2 Rao和Prasad模型试验

Rao和 Prasad[4]也通过模型试验研究了黏土斜坡地形条件下圆形锚板的抗拔承载力，其模型试验采用直径为5 cm的圆形锚板。该模型试验的所得的定性结论与文献[15]所得结论相同，即锚板的抗拔承载力随斜坡倾角的增大而降低。

由于Rao和Prasad的模型试验采用的是圆形锚板，而本文块体集上限分析研究的是条形锚板，因此，需要引入形状系数将圆形锚板的抗拔承载力转换为条形锚板的抗拔承载力。形状系数S的大小与锚板的埋深比（H/B）等诸多因素有关，其定义见式（1）。

式中：Nc0(circle)、Nc0(strip)分别为圆形锚板和条形锚板的抗拔承载力系数。

Rowe和Davis[9]利用弹塑性有限元方法分别分析了圆形锚板和条形锚板的抗拔承载力。图 6为Rowe和 Davis的弹塑性有限元分析结果，其中该分析采用的是k4破坏准则，即当锚板的位移等于弹性分析时所得到位移大小的4倍时，认为锚板处于极限破坏状态。图6中同时还给出了由该弹塑性有限元分析所得到的形状系数S。

图6 Rowe和Davis 弹塑性有限元分析所得到的形状系数[9]Fig.6 Shape factors of Rowe and Davis[9]

鉴于前文地表水平条件下，块体集上限分析结果与文献中的模型试验结果非常吻合。此处采用地表水平条件下（即斜坡倾角为 0°时），Rao和Prasad的圆形锚板模型试验数据与本文块体集上限分析所得到的条形锚板上限解相比，即由式（2）求得形状系数S，如图7中的黑色方块点所示。图 7中，D为圆形锚板的直径；H/D即为圆形锚板的埋深比，对于水平条形锚板而言，其锚板埋深比为H/B。同时，图7中分别给出了Merifield等[16]采用三维下限有限元分析得到的形状系数，以及由Rowe和Davis[9]的弹塑性有限元分析所得到的形状系数。由图可以看出，极限分析下限有限元分析得到的结果偏于保守，而本文的形状系数与Rowe和Davis的弹塑性有限元分析结果较为接近。

为便于应用，本文对由式（2）求得的形状系数S数据点进行了拟合，得到了本文所采用的形状系数计算公式：

当式（3）求得形状系数S＜1.15时，取S = 1.15。采用式（3）所示的形状系数，在斜坡地形条件下，本文块体集上限分析解与Rao和Prasad[4]的圆形锚板模型试验对比如图8所示。图8中，阴影部分表示当斜坡倾角由0°增大到45°时，块体集上限分析中锚板抗拔承载力的降低程度。由图可见，当锚板埋深比H/B比较小时，本文块体集上限分析预测与模型试验结果是比较吻合的，而H/B比较大时，模型试验结果中斜坡倾角的影响逐渐变小。如图8所示，当斜坡倾角为45°时，随锚板埋深比H/B的增大，其抗拔承载力与地表水平时相比差距逐渐变小。当 H/B＞4时，模型试验结果甚至出现了两条线基本重合的现象。对于模型试验而言，这说明在锚板埋深比比较大时，斜坡倾角对锚板抗拔承载力会降低到甚至可以忽略的程度，这一结论与本文块体集上限分析的理论预测完全相反。

图7 圆形锚板与条形锚板的形状系数Fig.7 Shape factors of circle and strip anchor plates

图8 斜坡地形下本文上限解与Rao和Prasad模型试验的对比Fig.8 Shape factors of circle and strip anchor plates

5 试验模型中拉杆的影响

Rao和 Prasad[4]模型试验中之所以会出现与本文块体集上限分析理论预测相反的情形，主要是该模型试验采用了图 1(a)试验模型，试验过程中拉拔力通过连接在锚板中点的金属拉杆来实现。因此，锚板的埋深比H/B越大，该金属拉杆在土体中埋置的长度就越大。而对于斜坡地形条件下块体集上限法对于锚板破坏面的分析结果，如图9所示。由图可以看出，当地表水平时，破坏面呈现对称的 U型，且拉杆处土体变形主要是竖直方向的。当斜坡倾角存在时，破坏面向坡脚方向倾斜，因此土体变形会倾向于向坡脚方向倾斜，原先在地表水平条件下所呈现的对称性不复存在。同时，由图9还可以看出，斜坡倾角越大，破坏面向坡脚方向的倾斜程度也越大。

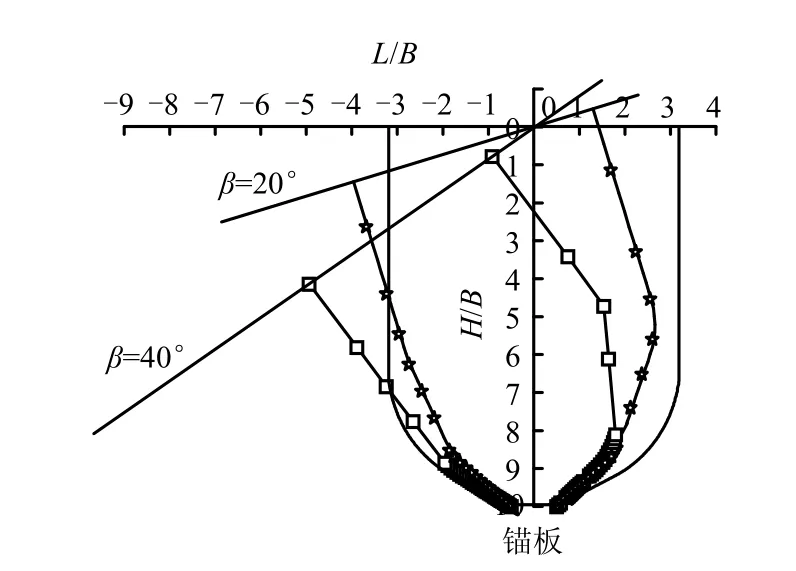
图9 不同斜坡倾角时水平条形锚板破坏面(H/B=10)[15]Fig.9 Failure surface of strip anchor plate at different slope angles (H/B=10)[15]

由图10(a)所示，对于地表水平条件下，由于模型试验中拉杆正好处于锚板破坏面的对称轴的位置，因此，拉杆对锚板抗拔承载力的影响主要体现在拉杆侧壁与土体的摩擦阻力上，当拉杆表面足够光滑时，摩擦阻力的影响完全可以忽略不计。而对于斜坡地形条件下（见图10(b)）可以明显的看到，拉杆的存在对土体向坡脚方向的变形有着明显的制约作用，因此拉杆的存在可以提高锚板抗拔承载力。由块体集上限分析可知，斜坡倾角和锚板埋深比H/B越大，锚板破坏时破坏面向坡脚方向的倾斜程度也越大，这就意味着土体在拉杆侧壁的法向方向的变形也越大，即拉杆对锚板抗拔承载力的贡献也越大，这就导致了Rao和Prasad[4]模型试验结果中，随着锚板埋深比H/B的增大，斜坡倾角对锚板抗拔承载力的降低部分越来越多的被拉杆的有利贡献所抵消。因此，Rao和Prasad模型试验所测得的试验数据实际上是锚板与拉杆协同作用下的抗拔承载力，这与研究锚板本身抗拔承载力的试验目标有着很大的区别。因此，由于拉杆的存在，Rao和 Prasad[4]的模型试验对于斜坡地形条件下锚板抗拔承载力的研究并不合理，尤其是在锚板埋深比H/B比较大时，由于拉杆的影响，该模型试验的试验结果甚至与本文块体集上限分析的理论预测趋势相反。

图10 模型试验中拉杆对锚板抗拔承载力的影响Fig.10 Effects of steel rod on pull-out capacity of anchor plates in laboratory test

鉴于此，对于斜坡地形条件下的浅埋锚板抗拔承载力研究，笔者认为应该尽可能采用从锚板底面施加推力的trapdoor模型，这样就可以避免土体中拉杆的存在，而使得模型试验结果能够更好的反映锚板本身的抗拔承载力。

6 结 语

通过块体集上限分析方法，本文研究了锚板的抗拔承载力和破坏面特性，并将分析结果与 Das[1]和Rowe[2]的锚板模型试验结果进行详细对比，验证了块体集上限法的有效性。然后运用块体集上限法分析了考虑斜坡地形的Khing等[3]条形锚板抗拔承载力试验，以及Rao和Prasad[4]的圆形锚板抗拔承载力试验，通过与模型试验结果的对比，分析了斜坡地形条件下模型试验中采用拉杆加载的方式对于试验结果的影响，并对锚板试验模型的选取提出了合理的建议，（1）对于地表水平条件下，锚板模型试验中拉杆的影响可以忽略，但是对于斜坡地形条件下，拉杆的影响不能忽略；（2）斜坡地形条件下，浅埋锚板的模型试验应尽可能采用trapdoor模型。

[1]DAS B M. A procedure for estimation of ultimate uplift capacity of foundations in clay[J]. Soils and Foundations,1980,20(1): 77－82.

[2]ROWE R. Soil structure interaction analysis and its application to the prediction of anchor plate behaviour[D].Sydney，Australia: University of Sydney,1978.

[3]KHING K H,DAS B M,YEN S C. Uplift capacity of strip plate anchors in clay with sloping surface[C]//Proc.4th International Offshore and Polar Engineering Conference. Japan: International Society of Offshore and Polar Engineers,1994: 467－471.

[4]RAO S,PRASAD Y. Uplift capacity of plate anchors in sloped clayey ground[J]. Soils and Foundations,1992,32(4): 164－170.

[5]DICKIN E A. Uplift behavior of horizontal anchor plates in sand[J]. Journal of Geotechnical Engineering,1988,114(11): 1300－1317.

[6]DICKIN E A,LAMAN M. Uplift response of strip anchors in cohesionless soil[J]. Advances in Engineering Software,2007,38(8-9): 618－625.

[7]MURRAY E J,GEDDES J D. Uplift of anchor plates in sand[J]. Journal of Geotechnical Engineering,1987,113(3): 202－215.

[8]MURRAY E J,GEDDES J D. Resistance of passive inclined anchors in cohesionless medium[J]. Geotechnique,1989,39(3): 417－431.

[9]ROWE R,DAVIS E. Behaviour of anchor plates in sand[J]. Geotechnique,1982,32(1): 25－41.

[10]DAS B M,SEELEY G R. Breakout resistance of shallow horizontal anchors[J]. Journal of the Geotechnical Engineering Division,1975,101(9): 999－1003.

[11]ROWE R,DAVIS E. Behaviour of anchor plates in clay[J]. Geotechnique,1982,32(1): 9－23.

[12]刘明亮,朱珍德,刘金元. 锚板抗拉破坏机制试验研究[J]. 岩土力学,2011,32(3): 697－708.LIU Ming-liang,ZHU Zhen-de,LIU Jin-yuan.Experimental study of failure mechanism of uplifting anchor[J]. Rock and Soil Mechanics,2011,32(3): 697－708.

[13]于龙,刘君,孔宪京. 锚板在正常固结黏土中的承载力[J]. 岩土力学,2007,28(7): 1427－1434.YU Long,LIU Jun,KONG Xian-jing. Stability of plate anchors in NC clay[J]. Rock and Soil Mechanics,2007,28(7): 1427－1434.

[14]GUNN M J. Limit analysis of undrained stability problems using a very small computer[C]//Proc.Symposium on Computer Applications to Geotechnical Problems in Highway Engineering. England: Cambridge University，1980: 5－30.

[15]余生兵,黄茂松. 基于组合块体集的浅埋条形锚板上限分析[J]. 岩石力学与工程学报,2011,30(5): 1049－1056.YU Sheng-bing,HUANG Mao-song. Upper bound analysis of horizontally embedded anchors based on block set mechanism[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(5): 1049－1056.

[16]MERIFIELD R S,LYAMIN A V,SLOAN S W,et al.Three-dimensional lower bound solutions for stability of plate anchors in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering,2003,129(3): 243－253.