偶应力对层状岩体结构面边界层效应的影响

张敦福，王相玉,，朱家明,，李术才，朱维申

（1.山东大学 土建与水利学院，济南 250061；2.清华大学 工程力学系，北京 100084；3.中国科学院力学研究所，北京 100190）

1 引 言

岩体是自然地质体，内部存在断层、层理、节理、裂隙等。岩石中两个以上的块体相互连接，荷载通过其连接界面传递而产生变形。由于接触问题属于力-位移混合边界问题，采用混合有限元（杂交单元）方法具有优势[1]。求解界面接触问题有多种方法，如接触单元法、Lagrange乘子法、罚方法等。完整岩块在有限元计算中可用常规的实体单元代表。节理是层状岩体中的不连续面，其厚度接近于0。对于重要节理，通常采用节理单元计算；对于不重要的节理，可采用等效单元计算。

经典连续介质理论认为，材料某点处应力仅是该点的应变以及该点的变形历史上的函数，而与该点以外的其他点的应力无关[2]。但由于连续性假设不能严格满足，因此，将连续介质力学应用于岩土介质时，应力和应变等分量代表的仅是相当小但不是无穷小体积上的统计平均值。

在应变梯度不大的情况下，使用统计平均值来替代连续介质力学理论解可以较为恰当地描述介质的力学反映。但当材料出现较高的应变梯度时，在相当小体积上，应变呈高阶非线性，经典理论所代表的统计平均值就不能真实地反映出材料在相当小的体积上的强度和变形行为。实质上，梯度项的出现反映这样一个事实：在某种尺度下的微结构相互作用使得变形是非局部的，应变梯度及内部长度描述的是不均质材料微结构之间的相互影响及作用。

偶应力理论在20世纪90年代初被引入岩土工程领域。Mühlhaus[3]的工作涉及层状岩体、节理岩体、层状半无限土体、岩煤和砂砾等。陈胜宏[4]、余成学[5]等率先开展研究，在这方面取得了开创性的成果。潘一山等[6]把微结构应变梯度理论应用于岩体力学，利用试验研究了岩石破坏的尺度效应，又提出了岩石失稳破坏的应变梯度模型，并给出了节理岩体内部特征长度的数值。其他学者也对这一理论进行了不同方面的研究。偶应力理论的有限单元法要求位移解满足C1连续，而一般单元只能满足C0连续，陈万吉[7]等很多学者在构造新的满足 C1连续的单元方面做了许多工作。Taiji Adachi等[8]采用罚函数强制宏观转角与微观转角相同提出了一种有限单元，但由于计算结果不理想，只好对将组成一个四边形的两个三角形单元中的一个实施惩罚，以提高计算精度。Fleck等[9]采用罚函数法放松了对旋转自由度的约束，取得了较好的效果。肖其林等[10]、李雷等[11]构造了非协调单元和杂交元，并用它分析了偶应力问题。杨乐等[12]、刘俊等[13]、冀宾等[14]将Cosserat介质元引入均匀化技术，建立层状岩体的复合等效本构关系，进行有限元数值模拟，验证了新模型的有效性和可行性。唐欣薇等[15]利用位移渐近展开技术和均匀化理论，建立了多尺度力学框架下的有限元平衡方程，重点考察了单胞尺寸对宏观力学性能的影响。

本文基于偶应力理论，采用有限单元法，研究层状岩体中界面边界层效应问题，分析了偶应力的尺度效应、材料特征长度、弹性模量等参数对界面边界层效应的影响。为了提高计算结果的精度，采用高次矩形单元中的Serendipity单元（S单元）。

2 有限元插值函数及位移插值

2.1 经典弹性理论

根据插值函数求法的不同，矩形单元可以分为Lagrange单元（L单元）和Serendipity单元（S单元）。由于这两族单元的插值函数求法不同，所以单元节点的分布也不相同，即L单元的单元内部包含节点，而S单元的内部没有节点，这也是Serendipity族单元的特点。由于Lagrange族高次单元的内部节点不影响单元间的连续性，它们能在单元范围上取消，以便减少单元矩阵的阶数，所以本文采用了图1的S单元，以避免出现在L单元内部的中间节点。

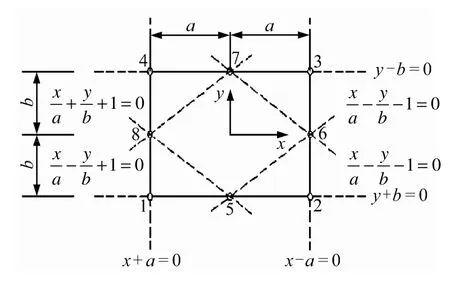
图1 S单元插值函数计算示意图Fig.1 An illustration of interpolation function for S-element

S单元的节点插值函数具有下列性质：

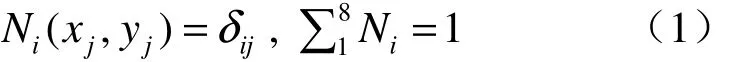
式中：Ni为节点插值函数； i,j=1,2,...,8；δij为克罗内克尔符号。

对于节点1的插值函数N1，在节点2，3，…，8上应取0值，在节点1上取单位值。相应的N1在x/a-1=0，y/b-1=0和x/a+y/b+1=0边界上为0。因此，假设N1为

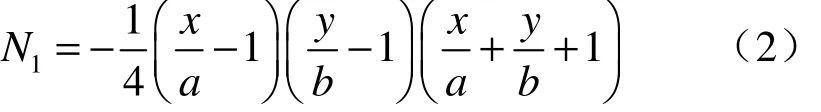
类似地，可以得到N1，N2，…，N8的表达式。现将插值函数一并列出

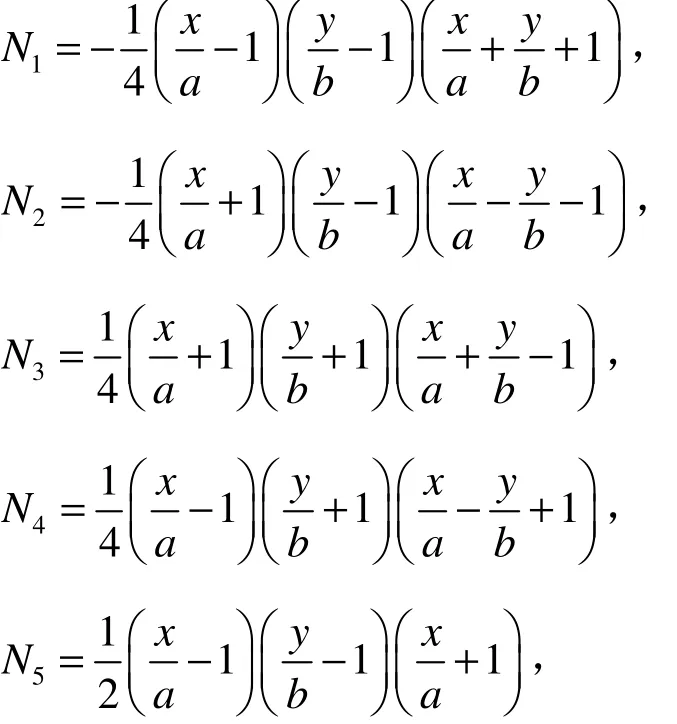
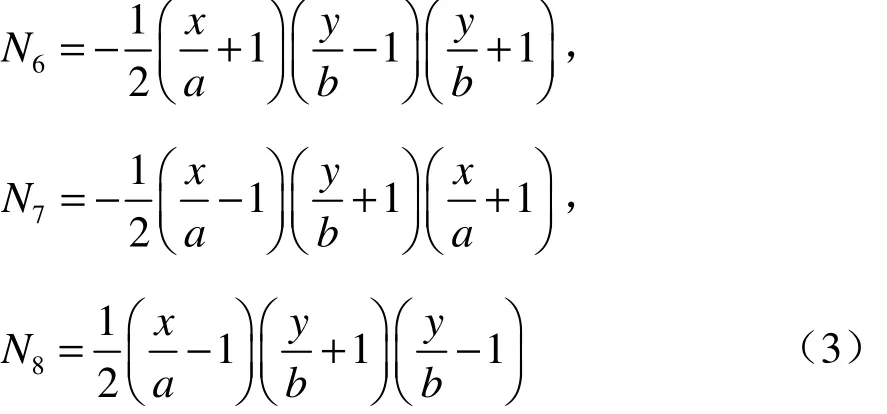
由插值函数的定义可知，单元内任一点的位移可以这样给出：

式中：ui、vi分别为节点i的位移分量；[N]=[N1⋅I N2⋅I…N8⋅I]（I为2阶单位矩阵）为插值函数矩阵；{δ}e为单元e上8个节点的位移。

2.2 弹性偶应力理论

弹性偶应力理论与经典弹性理论的区别主要在于引入了偶应力mx、my，即单位面积上的弯矩。平面微元体有3个自由度：2个平动分量和1个转动(旋转)分量。

由于偶应力的存在，剪应力互等定理不再成立，即τxy≠τyx。为了便于分析，将剪应力τxy和τyx写成对称分量τs和反对称分量τα两部分。即

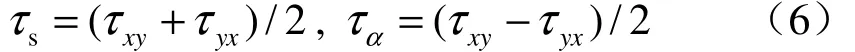
这样就可以很清楚地描述τs和τα的作用。即，τs使微元体产生剪切变形，τα使微元体产生宏观转动。如图2所示。

老机八从怀里掏出两块银元递给大勇：老子死了就帮俺捎给俺娘，跟俺娘说一声：娘，俺不能尽孝了。对了，老子万一活着呢，你得还把钱还给俺。

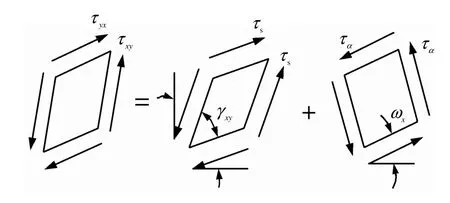
图2 微元体的变形Fig.2 Deformation of micro element

由于偶应力理论中单元有3个自由度，所以位移插值模式与以前有所不同，写成矩阵形式为

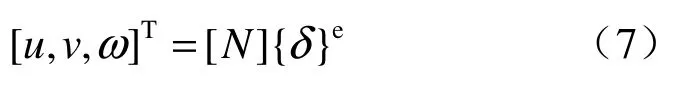
式中：u、v分别为节点i沿x轴和y轴方向的位移；ω为单元转角；[N]=[N1⋅I N2⋅I…N8⋅I ]（I为3阶单位矩阵）称为插值函数矩阵，是3×24阶矩阵；{δ}e为单元e上8个节点的位移，是24×1阶矩阵。所以，应变矩阵 [B ]=[B1B2… B8]。其中

3 层状岩体结构面边界层效应

3.1 偶应力理论和经典弹性理论结果比较

由于偶应力理论中剪应变γxy≠γyx，剪应力τxy≠τyx，所以偶应力理论下剪应变用(γxy+γyx)/2与经典弹性理论下剪应变γxy相比较；剪应力用(τxy+τyx)/2与经典弹性理论下剪应力τxy相比较。

如图3所示，层状岩体的两端受均布压力q=10 MPa和剪力τ=1 MPa。材料1的弹性模量与泊松比分别为E1=20 GPa、μ1=0.25，材料2的弹性模量与泊松比分别为E2= 40 GPa，μ2=0.25。材料1、2的特征长度为 l1=l2= 1 mm，第二剪切模量为 GC=0.5G，G为剪切弹性模量。

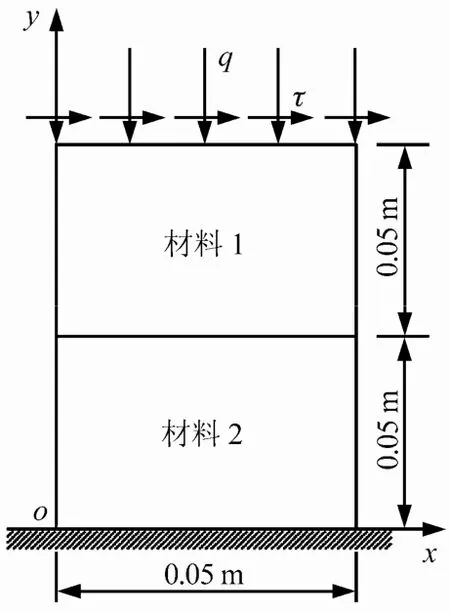
图3 层状岩体Fig.3 Layered rock mass

两种材料在节理面上满足以下假设：两种材料的界面黏合性好，无滑动、张开或嵌入。

定义图4所示路径，x坐标为0.025 m，y坐标为0.052～0.048 m。将该路径各应力、应变值的经典弹性理论和偶应力理论曲线绘于图5～10。

从图5～10可知，偶应力使得正应变、剪应变、主应变的绝对值减小。剪应变尺度效应明显，主应变和正应变尺度效应不明显。剪应变在边界层两侧出现了一个过渡区域，边界层两侧变化趋势一致。但剪应力在边界层附近不再连续，边界层两侧变化趋势一致。

3.2 弹性模量E2/E1的影响

取E2分别为40、60 GPa，其他参数同3.1节，考察 E2/E1对剪应力和剪应变的影响。图11给出了E2/ E1对剪应力、剪应变的影响曲线。

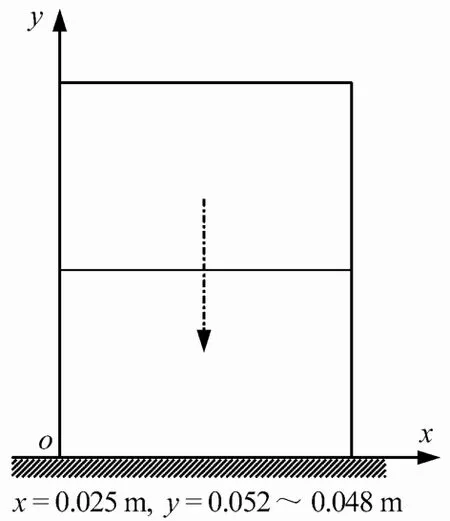
图4 计算路线Fig.4 Calculating route

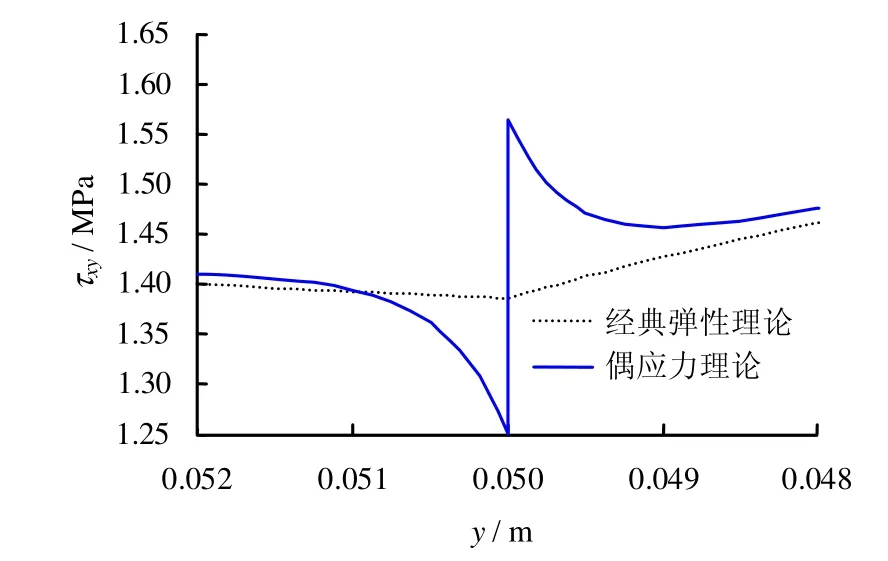
图5 剪应力Fig.5 Shear stress

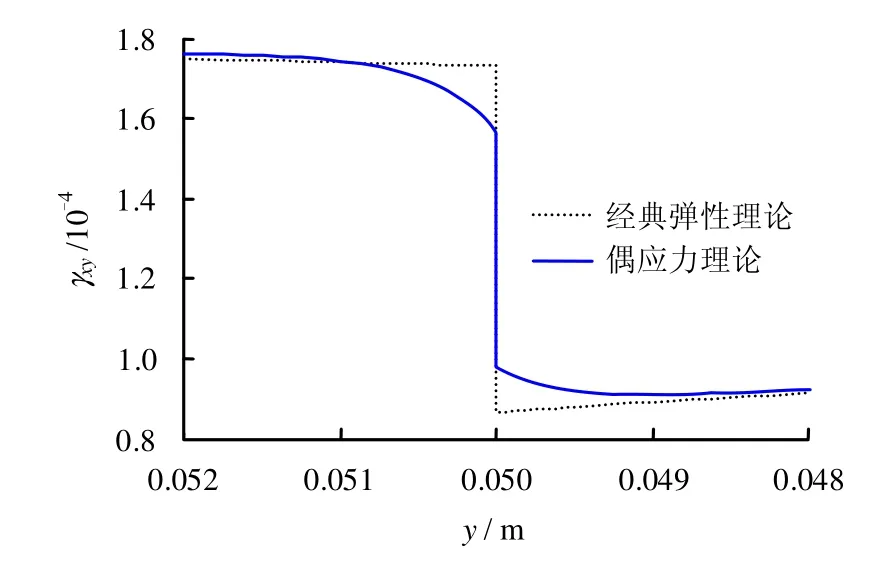
图6 剪应变Fig.6 Shear strain

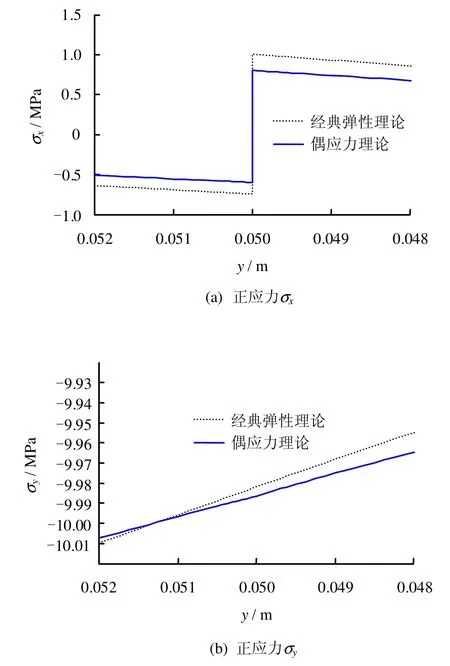
图7 正应力σx及σyFig.7 Normal stresses σxand σy

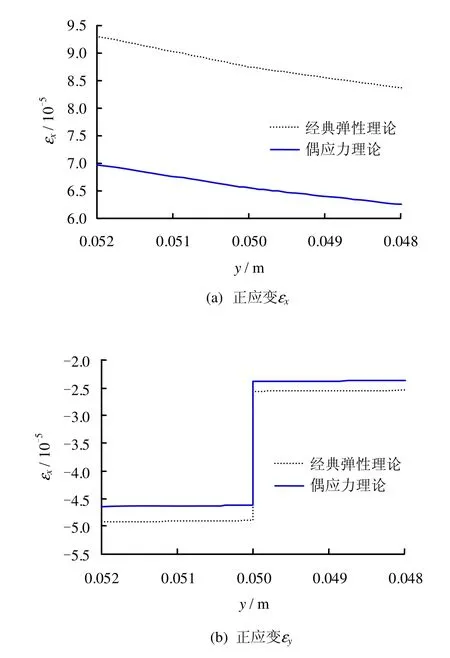
图8 正应变εx和εyFig.8 Normal strains εxand εy

图9 主应力σ1和σ3Fig.9 Principal stresses σ1and σ3

图10 主应变ε1和ε3Fig.10 Principal strains ε1and ε3

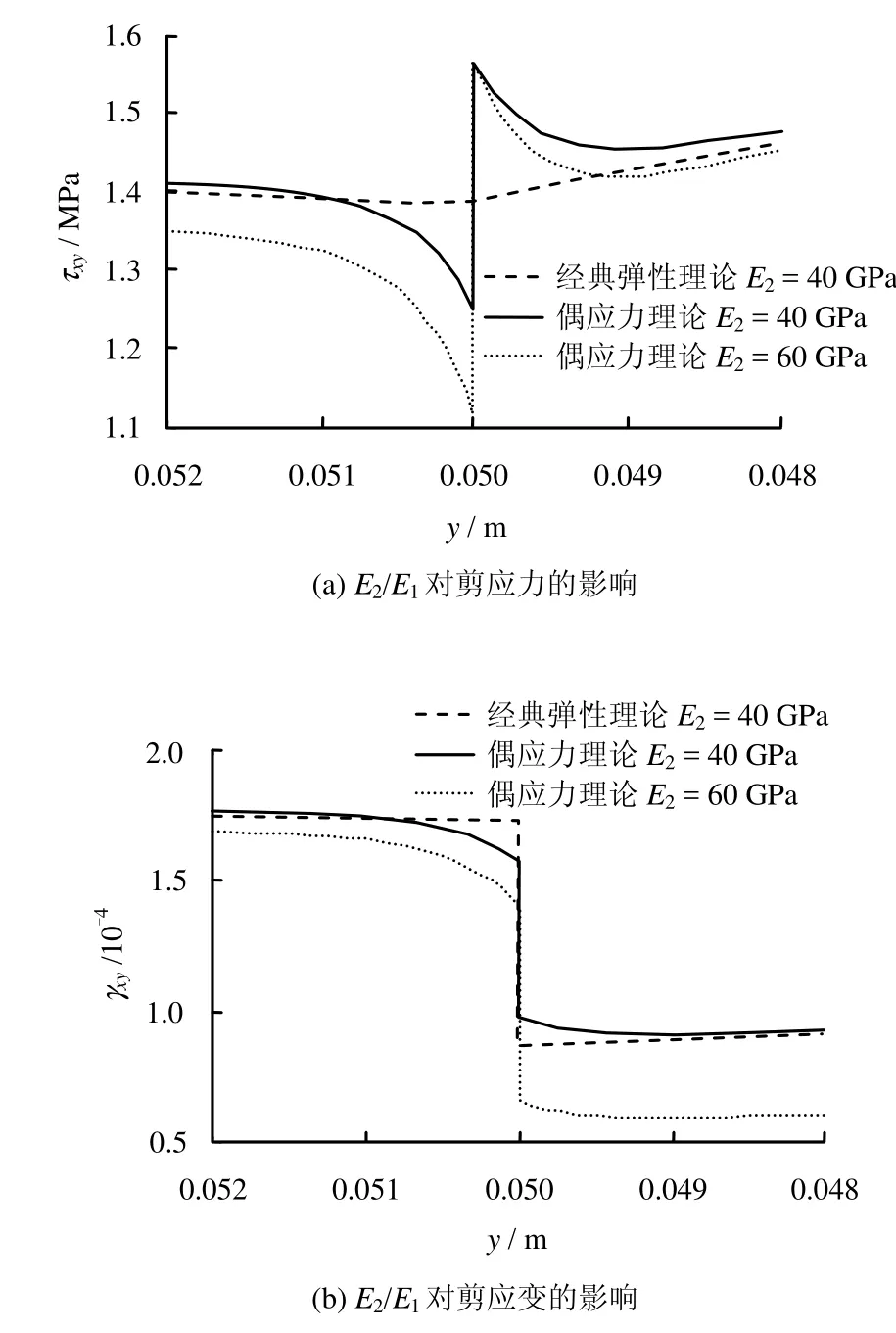
图11 E2/E1对剪应力、剪应变的影响Fig.11 Influences of E2/E1on shear stress and shear strain

从图11可以看出，弹性模量只对剪应力、剪应变的数值有影响，而不影响其变化趋势，即不影响边界层的范围。剪应力不再连续。

3.3 第二剪切弹性模量GC的影响

3.4 泊松比的影响

两种材料的泊松比μ依次取为0.18、0.25、0.32，其他参数与3.1节相同，考察μ对剪应力和剪应变的影响。图13给出了泊松比对剪应力、剪应变的影响曲线。从图可看出，泊松比不影响剪应力、剪应变过渡区域大小，不改变变化趋势，只影响剪应力、剪应变的大小。剪应力不再连续。

3.5 特征长度的影响

两种材料的特征长度l依次取为 0.5、1.0、2 mm，其他参数同3.1节，图14给出了特征长度对剪应力、剪应变的影响曲线。

图12 GC对剪应力及剪应变的影响Fig.12 Influences of GCon shear stress and shear strain

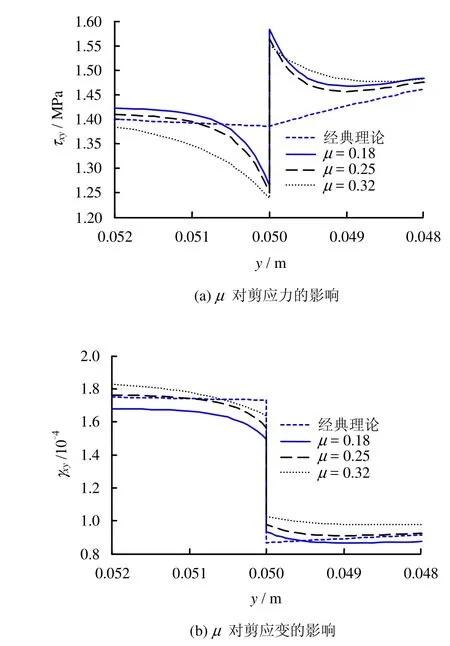
图13 μ 对剪应力及剪应变的影响Fig.13 Influences of μ on shear stress and shear strain

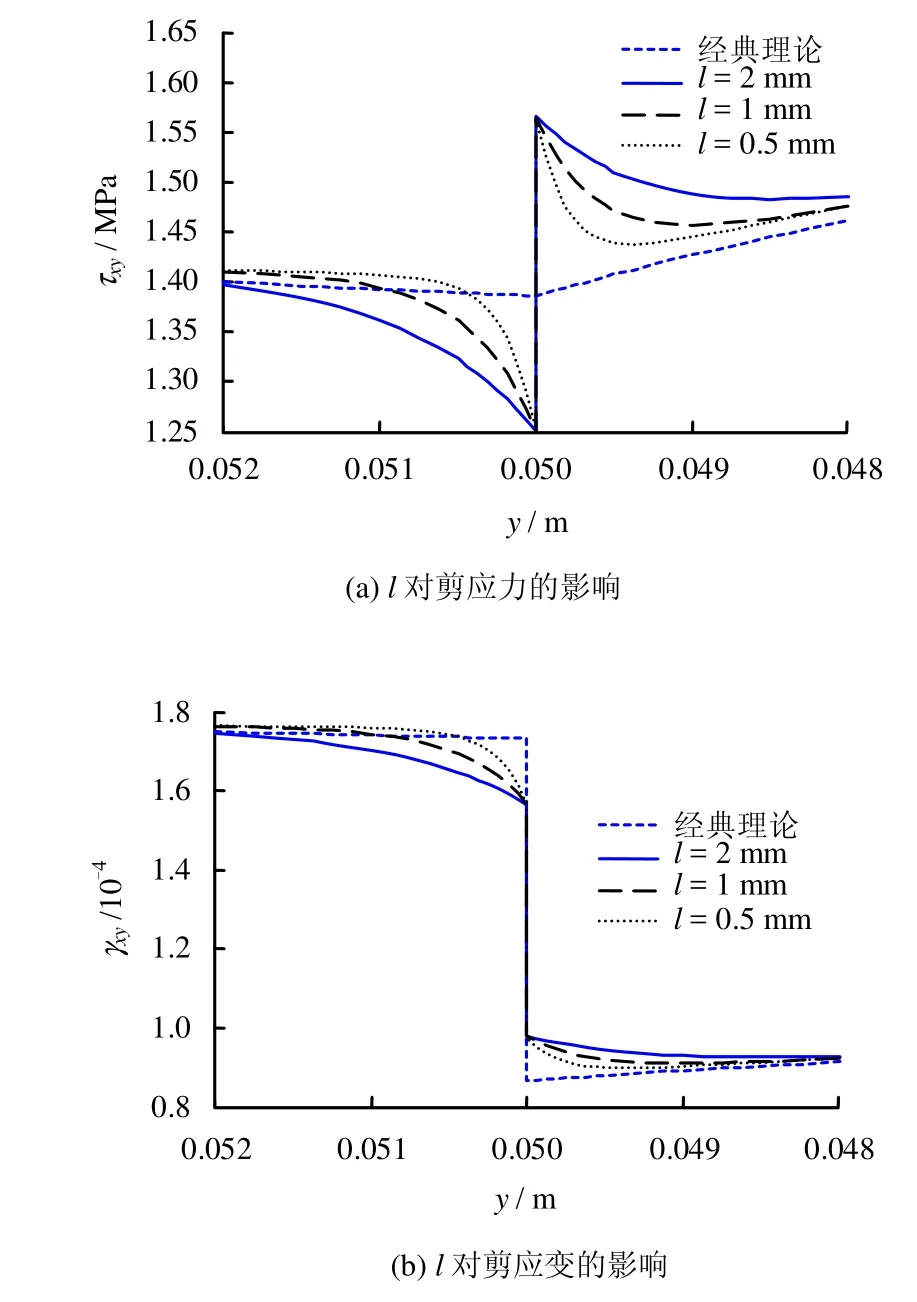
图14 l对剪应力及剪应变的影响Fig.14 Influences of l on shear stress and shear strain

从图 14可见，考虑偶应力后，剪应力、剪应变在边界附近出现了一个过渡区域。随着特征长度减小，剪应力、剪应变的过渡区域减小，在过渡区内斜率变大。剪应力不再连续。

4 偶应力对锚杆界面剪应力的影响

岩体中的拉拔锚杆，受力为400 kN，尺寸如图15所示。材料1为锚杆：直径为0.12 m，弹性模量E1=210 GPa，泊松比μ1=0.25；材料2为岩体：弹性模量E2=40 GPa，μ2=0.14。材料1、2的特征长度分别为l1=0.1 mm、l2=1 mm；两种材料的第二剪切模量取GC/G=0.5。

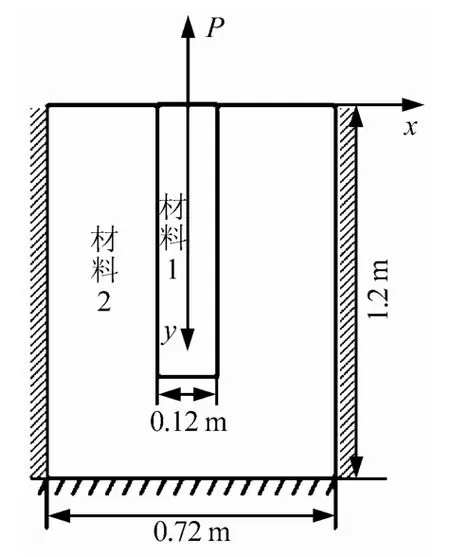
图15 拉拔锚杆Fig.15 Drawing bolt

两种材料在节理面上满足以下假设：两种材料的界面粘合性好、无嵌入。

图16给出了锚杆界面剪应力分布。由图可知，拉拔锚杆锚固段界面剪应力的分布集中在锚固段前部，呈先增大后衰减的趋势，最大值点到端头的距离约等于锚杆直径的一倍，这些结论与文献[16－19]一致。图17为沿x轴的剪应变及剪应力分布。由图可知，考虑偶应力后，界面上剪应力分布没有明显变化，偶应力对剪应力峰值有明显影响。剪应力、剪应变在界面附近出现了一个过渡区域，并且剪应力不再连续。

图16 锚杆界面剪应力Fig.16 Shear stress in the interface between bolt and rock

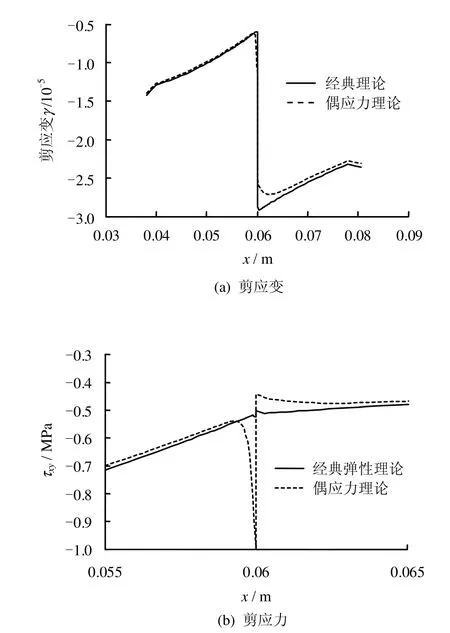
图17 沿x轴的剪应变及剪应力Fig.17 Shear stress and shear strain along x-axis

5 结 论

（1）在边界层内，存在一定的转动梯度效应，偶应力不为0，界面处剪应力不再连续。

（2）偶应力对层状岩体结构面剪应变有显著影响，尺度效应明显。在偶应力理论下，应变量减小，并在边界层附近出现过渡区，剪应变突变现象得以改善，但剪应力不再连续。

（3）材料特征长度对剪应变和剪应力的过渡区域大小有影响。随着特征长度的减小，过渡区域减小，剪应变和剪应力在过渡区域内斜率增大，即应变梯度增大，尺度效应更加明显。

（4）第二剪切模量 GC对剪应变和剪应力的过渡区域大小没有影响。随着 GC增大，剪应变和剪应力在过渡区域内斜率增大，即应变梯度增大，尺度效应更加明显。

（5）泊松比、弹性模量对剪应变和剪应力的过渡区域大小没有影响，只影响界面处剪应变和剪应力的大小，不改变剪应变和剪应力的变化趋势。

（6）锚杆界面剪应力的分布集中在锚固段前部，呈先增大后衰减的趋势，最大值点到端头的距离约等于锚杆直径的一倍。偶应力不改变锚杆界面上的剪应力分布，但对峰值有明显的影响，峰值变小，说明锚杆的抵抗外载的能力变大。

[1]张楚汉. 论岩石、混凝土离散-接触-断裂分析[J]. 岩石力学与工程学报,2008,27(2): 217－235.ZHANG Chu-han. Discrete-contact-fracture analysis of rock and concrete[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(2): 217－235.

[2]赵冰,李宁,盛国刚,等. 应变梯度理论在岩土力学中的进展述评[J]. 长沙交通学院学报,2005,21(1): 47－52.ZHAO Bing,LI Ning,SHENG Guo-gang,et al. A survey of strain gradient applied in rock and soil mechanics[J].Journal of Changsha Communications University,2005,21(1): 47－52.

[3]MÜHLHAUS H. B. Stress and couple stress in a layered half plane with surface loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics,1990,14(8): 545－563.

[4]陈胜宏,王鸿儒,熊文林. 节理岩体的偶应力的影响研究[J]. 水利学报,1990,(1): 44－48.CHEN Sheng-hong,WANG Hong-ru,XIONG Wen-lin.The effect of couple stress on jointed rock mass[J].Journal of Hydraulic Engineering,1990,(1): 44－48.

[5]余成学,熊文林,陈胜宏. 层状岩体的弹黏塑性Cosserat介质理论及其工程应用[J]. 水利学报,1996,(4): 10－17.SHE Cheng-xue,XIONG Wen-lin,CHEN Sheng-hong.Elastovisco-plastic Cosserat theory of layered rockmass and its application to engineering[J]. Journal of Hydraulic Engineering,1996,(4): 10－17.

[6]潘一山,袁旭东,章梦涛. 岩石失稳破坏的应变梯度模型[J]. 岩石力学与工程学报,1998,17(增刊): 760－765.PAN Yi-shan,YUAN Xu-dong,ZHANG Meng-tao.Model of gradient strain about failure rockmass with instability[J]. Chinese Journal of Rock Mechanics and Engineering,1998,17(Supp.): 760－765.

[7]陈万吉. 应变梯度理论有限元 C0-1分片检验及其变分基础有限元增强型分片检验[J]. 大连理工大学学报,2004,44(4): 474－477.CHEN Wan-ji. Finite element methods in strain gradient theory: C0-1patch test and its variational basic[J]. Journal of Dalian University of Technology,2004,44(4): 474－477.

[8]ADACHI T,TOMTA Y,TANAKA M. Computational simulation of deformation behavior of 2D lattice continuum[J]. International Journal of Mechanical Sciences,1998,40(9): 857－866.

[9]FLECK N A,SHU J. Microbuckle initiation in fibre composites: A finite element study[J]. Journal of the Mechanics and Physics of Solids,1995,43(12): 1887－1918.

[10]肖其林,凌中,吴永礼. 偶应力问题的杂交-混合元分析[J]. 计算力学学报,2003,20(4): 427－433.XIAO Qi-lin,LING Zhong,WU Yong-li. Hybrid-mixed finite element analysis of couple stress problems[J].Chinese Journal of Computational Mechanics,2003,20(4): 427－433.

[11]李雷,吴长春. 基于Cosserat理论的应变梯度非协调数值研究[J]. 工程力学,2004,21(5): 166－171.LI Lei,WU Chang-chun. Incompatible finite element for materials with strain gradient effects[J]. Engineering Mechanics,2004,21(5): 166－171.

[12]杨乐,吴德伦,李德万,等. 层状岩体的 Cosserat介质均匀化[J]. 应用力学学报,2010,27(1): 96－100.YANG Le,WU De-lun,LI De-wan,et al. Homogenization method for layered rock mass as Cosserat medium[J]. Chinese Journal of Applied Mechanics,2010,27(1): 96－100.

[13]刘俊,黄铭. 考虑偶应力影响的双组节理岩体等效模型[J]. 长江科学院院报,2010,27(9): 43－46.LIU Jun,HUANG Ming. Equivalent model of rock-masses with two sets of joints considering influence of couple stresses[J]. Journal of Yangtze River Scientific Research Institute,2010,27(9): 43－46.

[14]冀宾,陈万吉,赵杰. 基于偶应力理论剪切带问题的弹塑性有限元分析[J]. 力学学报,2009,41(2): 192－199.JI Bin,CHEN Wan-ji,ZHAO Jie. Elastoplastic finite element analysis of shear band with couple stress theory[J]. Chinese Journal of Theoretical and Applied Mechanics,2009,41(2): 192－199.

[15]唐欣薇,张楚汉. 基于均匀化理论的混凝土宏细观力学特性研究[J]. 计算力学学报,2009,26(6): 876－881.TANG Xin-wei,ZHANG Chu-han. Study of concrete in macro and meso scale mechanical properties based on homogenization theory[J]. Chinese Journal of Computational Mechanics,2009,26(6): 876－881.

[16]赵同彬,尹延春,谭云亮,等. 锚杆界面力学试验及剪应力传递规律细观模拟分析[J]. 采矿与安全工程学报,2011,28(2): 220－224.ZHAO Tong-bin,YIN Yan-chun,TAN Yun-liang,et al.Mechanical test of bolt interface and microscopic simulation of transfer law for shear stress[J]. Journal of Mining & Safety Engineering,2011,28(2): 220－224.

[17]贺若兰,张平,李宁,等. 拉拔工况下全长粘结锚杆工作机理[J]. 中南大学学报,2006,37(2): 401－407.HE Ruo-lan,ZHANG Ping,LI Ning,et al. Working mechanism of fully grouted bolt in pull-out working state[J]. Journal of Central South University,2006,37(2): 401－407.

[18]陈浩,任伟中,李丹,等. 深埋隧道锚杆支护作用的数值模拟与模型试验研究[J]. 岩土力学,2011,32(增刊1):719－786.CHEN Hao,REN Wei-zhong,LI Dan,et al. Numerical simulation and model test study of mechanism of bolt in deep tunnel[J]. Rock and Soil Mechanics,2011,32(Supp.1): 719－786.

[19]张幼振,石智军,张晶. 岩石锚杆锚固段荷载分布试验研究[J]. 岩土力学,2010,31(增刊2): 184－188.ZHANG You-zhen,SHI Zhi-jun,ZHANG Jing.Experimental study of load distribution of anchoring section for rock bolts[J]. Rock and Soil Mechanics,2010,31(Supp. 2): 184－188.