裂隙岩体渗流-应力耦合等效渗流阻模型
2012-11-05刘卫群
陶 煜,刘卫群
(1.中国矿业大学 力学与建筑工程建学院,江苏 徐州 221116;2.中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221116)
1 引 言
在岩土工程实践中,经常会遇到水文地质条件较为复杂的环境,受到多类水体运移及裂隙渗流作用的影响[1]。为了考察区域应力作用下裂隙岩体中复杂的渗流状态,需要对其内部裂隙发育以及这些裂隙在应力作用下的渗流规律进行分析,一些国内学者已对此进行了相关的研究[2-4]。大量关于采动岩体渗流的试验和实测结果表明,其渗透特性随应力场改变而发生显著变化。由于应力场变化导致区域裂隙系统的发育程度和组织形态的改变,因此,渗透率的改变与裂隙系统的发育程度和组织形态变化有着密切的联系。
为此,区域裂隙系统的发育程度和组织形态成为本文研究工作的切入点。图1是选自文献[2]的关于不同采厚工作面推进200 m采动裂隙演化过程及形态特征图。
通过观察不难发现,裂隙岩体主干裂隙的演化有一个明显的特征。就是在一段区域内,主干裂隙是沿着一定的方向发育的,并且存在分叉的现象。由于主干裂隙在区域裂隙系统中分布较为明显,其贯通程度、裂隙张开度、跨越区域都超过非主干裂隙,所以在裂隙渗流中起着主导作用。因此,考虑区域主干裂隙应力影响下的渗流规律对分析裂隙岩体渗流特性具有重要意义。
为了考察贯通区域主干裂隙系统的渗透能力,本文运用平行板渗流立方定律,结合弹性力学方法和模拟电路知识,建立了一种基于等效渗流阻的渗流-应力耦合模型。通过该模型可以进一步地分析这种贯通主干裂隙系统受应力作用的渗流演化规律。
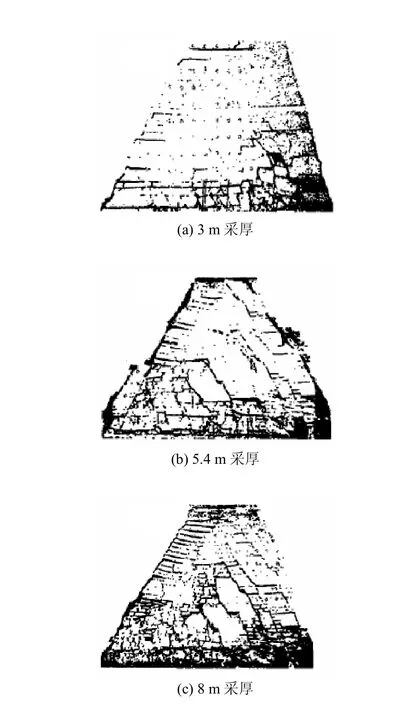
图1 不同采厚工作面推进200 m采动裂隙演化过程及形态特征[2]Fig.1 Evolutions and configuration characteristics of MIF in caving 200 m with different mining thicknesses [2]
2 裂隙岩体平行板模型
对厚度为a、隙宽为b的平行板裂隙均匀流,运用平行板渗流立方定律有
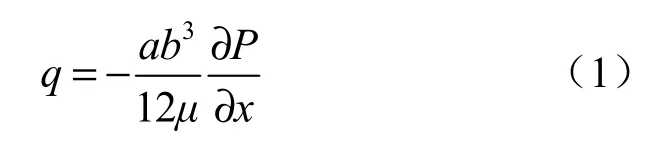
式中:q为流量;P为水压;μ为水的动力黏滞系数,其值与温度有关。
假若裂隙方向与流速为v,截面积为S的水流方向成α角度,则
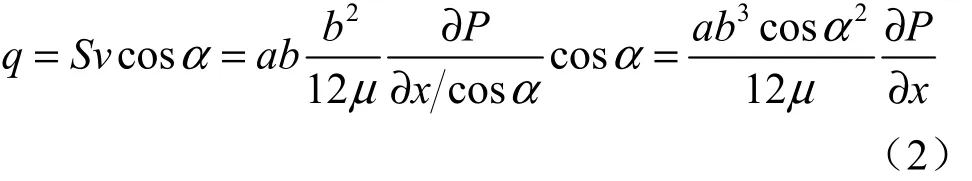
式(2)是单裂隙平行板模型隙宽与单宽流量之间的关系[5]。岩石中实际的壁面是粗糙的,若将由光滑平行板缝隙层流流态导出的立方定律用于实际裂隙,则需要对立方定理进行修正。实际裂隙面起伏不平,有许多凸体,致使水流在同一水力梯度下,同一隙宽的粗糙裂隙比光滑裂隙通过的流量要小。Ломизе[6]进行了粗糙裂隙水力试验,发现裂隙面的突起度 Δ与隙宽的比值对裂隙过流能力有很大影响。他将立方定理加入了一个粗糙度修正系数C,
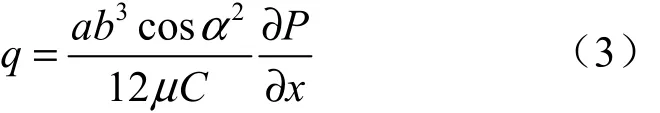
很多学者根据试验或理论提出了各自的粗糙度修正公式,主要有 Ломизе(1951)、Louis(1967),Neuzil(1981)、Tsang(1981)、Barton(1985)、周创兵(1996)等。王媛和速宝玉[7]已就该方面的文献进行了综述。
取垂直于x轴的裂隙截面宽度为bv,则裂隙宽b=bvcosα ,则式(3)改写为
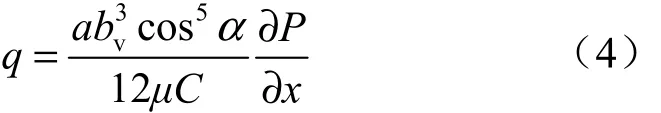
3 渗流等效流阻模型的建立
天然裂隙岩体中的裂隙分布多种多样,一般可分为较为离散细微的裂隙网络和较大尺度的主干裂隙系统。前者参与渗流过程程度相对较弱,且运用连续介质理论方法处理较为成熟。而后者在贯通程度、张开度、跨越区域都优于前者,参与渗流作用的比重远大于前者。作为渗流作用主体,主干裂隙系统成为本文渗流分析的主要对象。
图2选自Nick Barton的岩体节理(Rock Joints)一书[8],展现了不同岩体的裂隙分布。可以较为明显地观察出主干裂隙系统与离散的裂隙网络。在裂隙岩体中,主干裂隙系统是由有限个单裂隙组合而成。而每一个单裂隙之间仅有如图3所示的2种基本组合关系。
本文对这两种组合关系下的渗流特性分别进行讨论。
3.1 串联关系
如图4所示,根据b1裂隙的流量和b2裂隙的流量相等的特点,有

式中:qf为裂隙流量;Δp为水的压力差;α1、α2分别为上下部分裂隙的厚度;b1、b2分别为上下部分裂隙的宽度;Δx1、Δx2为上下部分裂隙的长度;α1、α2分别为上下裂隙分别与流动方向之间的夹角。在图4中α1、α2都为0°。
而 Δp=Δp1+Δp2(如图4所示),所以
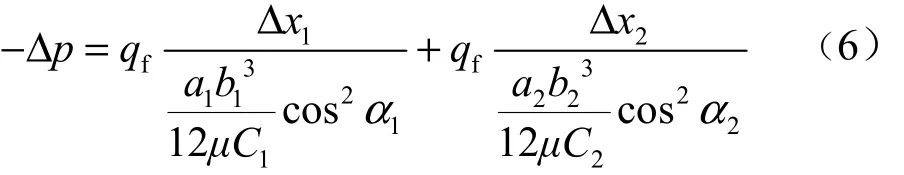

图2 几种岩体裂隙图[8]Fig.2 Fractures in several kinds of rock masses[8]
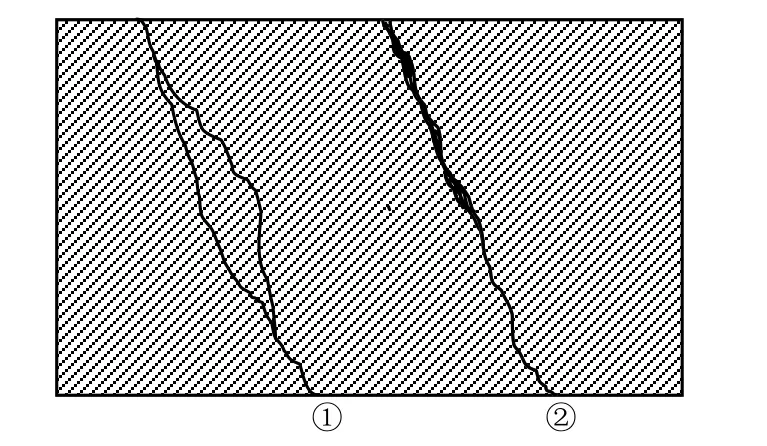
图3 裂隙基本组合关系图Fig.3 Relationship of fracture combinations
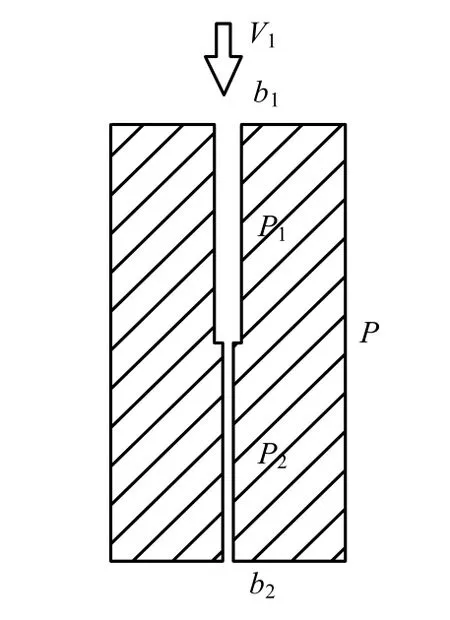
图4 串联情形平行板裂隙渗流系统Fig.4 Fracture seepage system in series
而在模拟电路中,串联公式为 U=IR1+IR2,由式(6)可以看出在裂隙渗流中存在类似电路串联关系。
3.2 并联关系
两裂隙并联,如图5所示,根据裂隙系统总流量等于b1裂隙流量和b2裂隙流量之和,可以得出
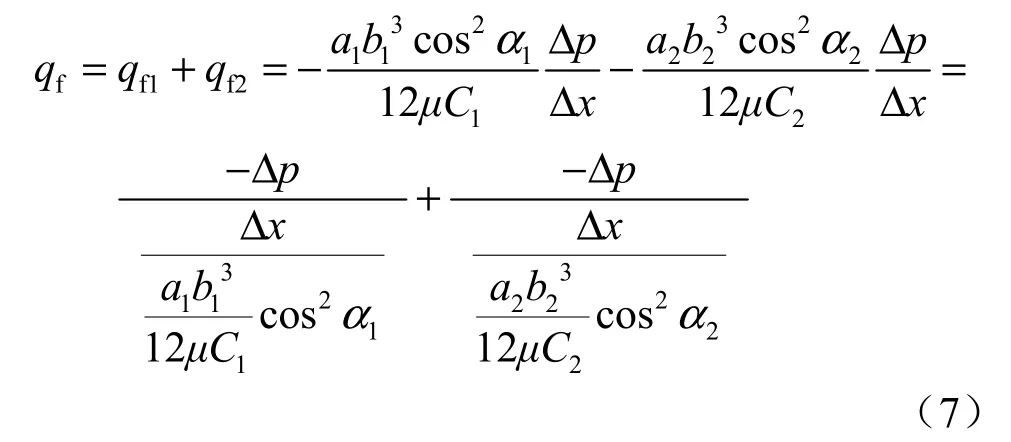
式中:α1、α2分别为左右两个裂隙分别与流动方向之间的夹角。在图5中α1、α2都为0°。
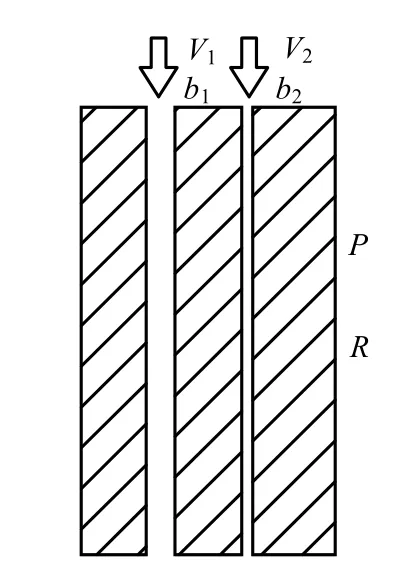
图5 并联情形平行板裂隙渗流系统Fig.5 Fracture seepage system in parallel
所以,根据式(7)我们可以得到在裂隙渗流中存在类似电路并联的关系。
因此,可以把区域主干裂隙中的流体渗流等效为模拟电路中的串并联电路群,两者之间的相似量如表1中给出。
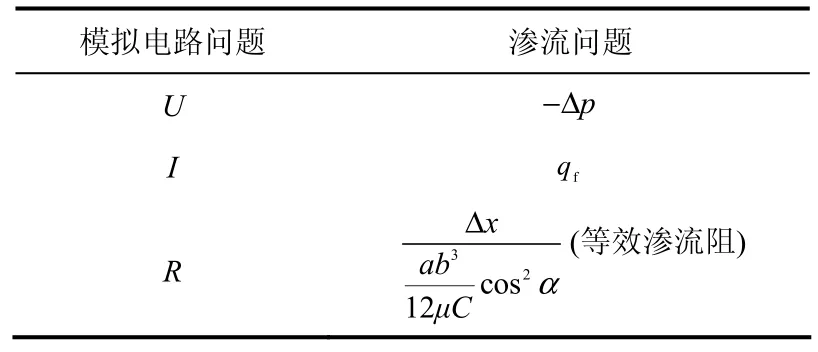
表1 模拟电路问题与渗流问题中的相似量表Table1 Similar capacities between electronics and seepage problems
假设一个区域主干裂隙系统有i个层次,即i层串联等效渗流阻,每个层次有j个并联等效渗流阻,那么此区域主干裂隙系统内的等效渗流阻Rf为
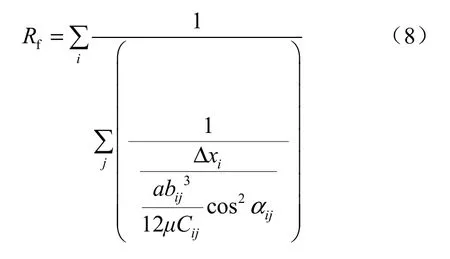
式中:bij、Cij、α分别为裂隙系统第i层串联部分里的第j个并联裂隙隙宽、裂隙粗糙度修正系数和裂隙与水流方向夹角。
裂隙系统流量为
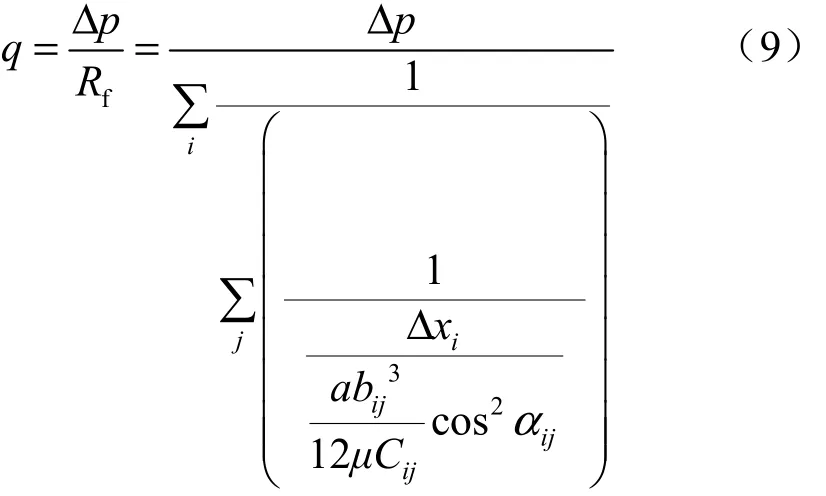
由于裂隙系统的渗透率k与等效渗流阻之间的关系为
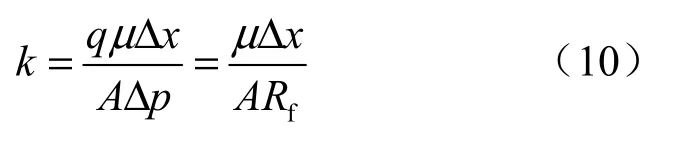
式中:A为渗流截面积。
故此裂隙系统的渗透率为
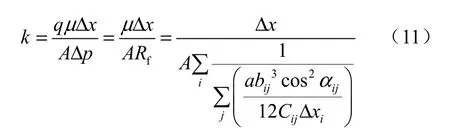
本文称这种由等效渗流阻构成的串并联渗流模型为“等效渗流阻模型”。
4 裂隙岩体应力与渗透率之间的关系
岩体中的应力变化导致裂隙宽度的变化,进而导致岩体渗透性的改变。为了探究裂隙岩体区域裂隙系统应力与渗透率之间的关系,假设在同一裂隙网络中同一层面上分布着n条裂隙,如图6所示。
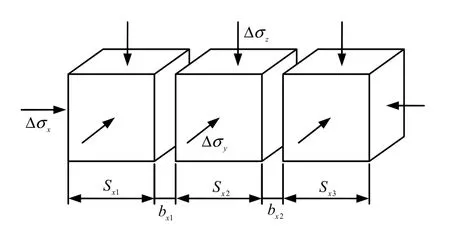
图6 三向应力条件下裂隙岩体应力-渗透性计算模型Fig.6 3D stress-permeability model for fractured rock mass
沿 x方向的岩体总位移Δutx等于裂隙的位移Δ ufx与岩块位移 Δurx之和,所以
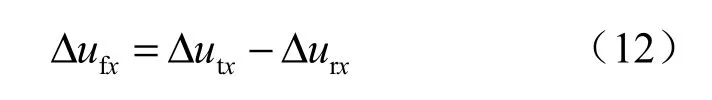
位移用应变表示有
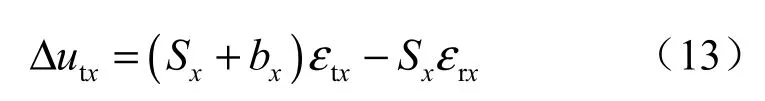
式中:Sx、bx分别为岩体的宽度和多条裂隙沿x 方向的宽度和。
沿x方向岩体应变εtx又可表示为
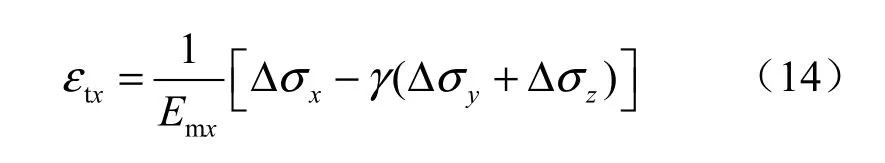
式中:Emx为裂隙岩体在x方向上的弹性模量;γ为泊松比;σx、σy、σz分别为x、y、z方向上的应力。
沿x方向岩块应变εrx可表示为

式中:Er为岩块的弹性模量。
由此,可得到多条裂隙的隙宽变化总量


如果这j条裂隙位于第i层串联中,那么式(19)可以改为
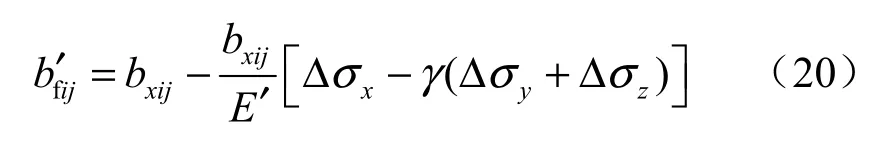

还可以进一步得到应力影响下该裂隙系统的渗透流量为
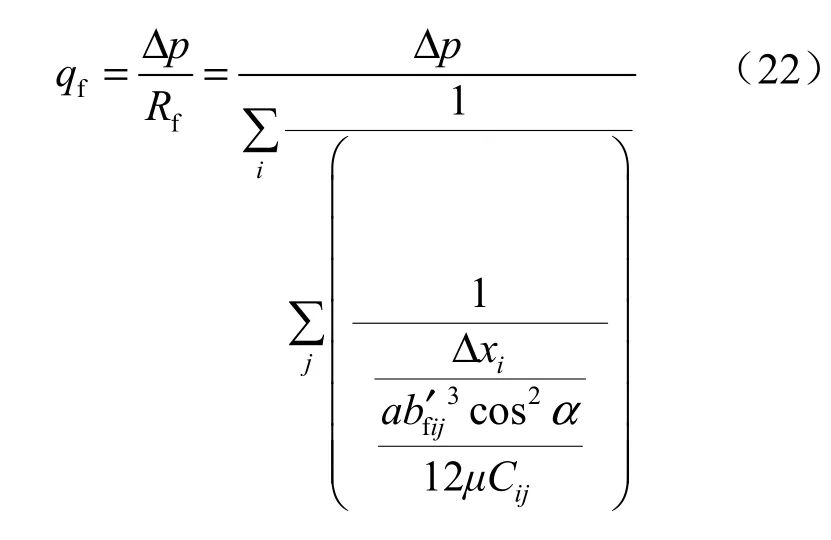
以及渗透率与应力之间的关系为
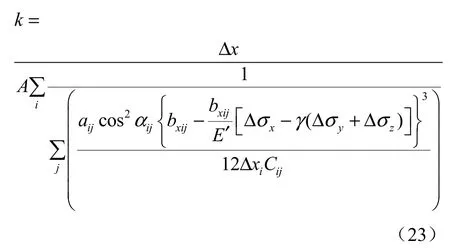
以上为本文建立的基于等效渗流阻的应力耦合渗流模型,可以用于分析应力作用下含区域主干裂隙岩体渗流演化规律。
5 算 例
结合上文建立的应力耦合等效渗流阻模型,选择含典型的“人”字形组合裂隙系统的 50 mm×50 mm×100 mm立方体岩石试样进行渗流分析,通过 Matlab计算程序考察该组合裂隙系统试样的渗流特性,分析对象如图7所示。
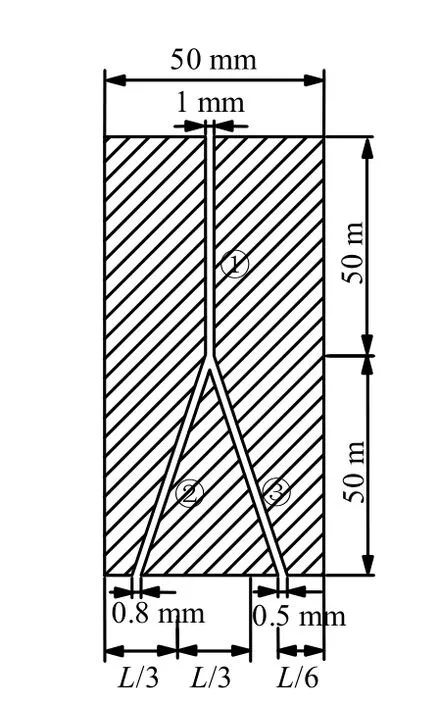
图7 50 mm×50 mm×100 mm立方体裂隙岩样图Fig.7 50 mm×50 mm×100 mm cubic fractured rock sample

表2 全局参数设定表(以国际单位制计)Table2 Global parameters (using SI units)

表3 各条裂隙参数赋值表(以国际单位制计)Table3 Parameters of each fracture (using SI units)
在众多粗糙度修正公式中,由于裂隙面粗糙度修正系数修正法相对于隙宽密度分布修正法等其他方法而言较为简便,并且其使用限制为裂隙面必须高度分布比较均匀,而本算例符合其使用条件。所以在计算中运用了Louis根据试验总结出的粗糙度修正公式
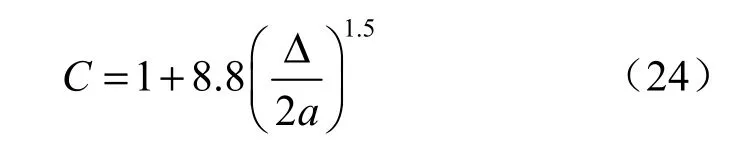
设岩石中水温为15 ℃,则 μ=1.14×10-3N⋅ s/m2。当Er=1 GPa,γ=0.2,μ=1.14×10-3N⋅ s/m2(具体各类参数如表2、3所示),且岩体中仅存在裂隙法向应力σx时,通过本文建立的裂隙等效渗流阻模型,可得出应力与等效渗流阻的关系曲线,如图 8所示。渗流阻与应力关系曲线表明,随着裂隙面法向应力的增加,裂隙系统等效渗流阻不断增加,两者呈幂函数关系递增。也可以得到渗透率与应力之间的关系曲线,如图9所示。图中渗透率与应力关系曲线显示,随着裂隙法向应力的增加,裂隙系统的渗透率不断减少,呈幂函数关系递减。

图8 渗流阻与应力的关系Fig.8 Seepage resistance-stress relationship
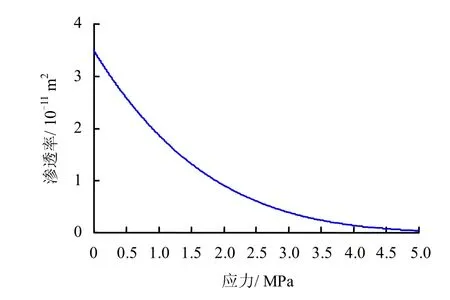
图9 渗透率与应力的关系Fig.9 Permeability-stress relationship
6 模型的扩展性探讨
等效渗流阻模型具有一定的可扩展性,有很多可以继续开展工作的地方,例如将等效渗流阻模型与有限元相结合,可以将裂隙系统划分为若干子裂隙系统,如图10所示。其中A~F为子裂隙系统,而 P1~ P9为联系这些子系统的裂隙出入口水压。
各子裂隙系统在应力场中所受的应力不同,而在子裂隙系统内可以将应力简化为相同。故子裂隙系统的尺寸与应力场的应力梯度分布相关,应力变化缓慢的地方可以选择相对较大的子裂隙系统尺寸,反之则应该选择较小的尺寸。经过进一步细分后,可将等效渗流阻模型与有限元分析方法结合起来,对大范围含裂隙岩体渗流区域应力场中主干裂隙系统的渗流演化规律进行分析。
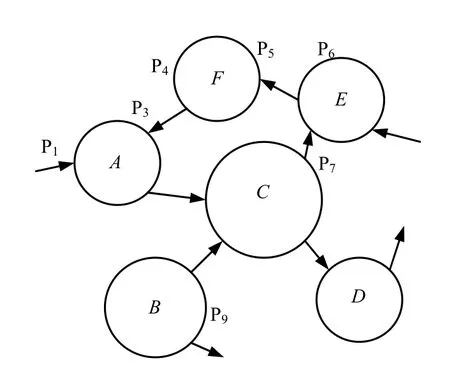
图10 子裂隙系统渗流图Fig.10 Seepage in subsystem of fractures
7 结 论
等效渗流阻模型具有以下优点:
(1)由于采用现实裂隙构造,无需求解复杂的偏微分方程,较随机裂隙网络等其他模型更为实用。
(2)在一个区域裂隙系统内我们定义了“渗流阻”的概念,不去分个考虑每个裂隙的应力状态下的渗流规律,化繁为简,利用区域渗流阻整体考虑它在整体应力影响下的渗流规律,分析问题更为方便有效。
(3)模型基于平行板渗流理论、模拟电路、弹性力学知识,具有普适性和可扩展性强的优点,更客观地描述应力变化下的区域主干裂隙系统的渗流规律。
由于并联裂隙情形采用等间距平行板模型简化,当分叉裂隙走向不同时存在一定误差,但沿高应力方向裂隙取向相近实际区域主干裂网中非常普遍,基本能满足模型要求。
文中模型经进一步细化后,可为岩体渗流分析问题提供理论支持。
[1]ZHANG J,SHEN B. Coal mining under aquifers in China:A case study[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(4): 629-639.
[2]杨科,谢广祥. 采动裂隙分布及其演化特征的采厚效应[J]. 煤炭学报,2008,33(10): 1092-1096.YANG Ke,XIE Guang-xiang. Caving thickness effects on distribution and evolution characteristics of mining induced fracture[J]. Journal of China Coal Society,2008,33(10): 1092-1096.
[3]陈占清,缪协兴,刘卫群. 采动围岩中参变渗流系统的稳定性分析[J]. 中南大学学报(自然科学版),2004,35(1): 129-132.CHEN Zhan-qing,MIAO Xie-xing,LIU Wei-qun.Analysis of stability of parametric system of seepage flow in wall rock affected by mining[J]. Journal of Central South University (Natural Science),2004,35(1): 129-132.
[4]张永波,靳钟铭,刘秀英. 采动岩体裂隙分形相关规律的实验研究[J]. 岩石力学与工程学报,2004,23(20):3426-3429.ZHANG Yong-bo,JIN Zhong-ming,LIU Xiu-ying.Testing study of fractal correlation law of cracks in mined rock mass[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(20): 3426-3429.
[5]周志芳. 裂隙介质水动力学原理[M]. 北京: 高等教育出版社,2007.
[6]Ломизе М. Филътрация в трещиноватых породах[M].Москва: Госэнергоиздат,. 1951.
[7]王媛,速宝玉. 单裂隙面渗流特性及等效水力隙宽[J].水科学进展,2002,13(1): 61-67.WANG Yuan,SU Bao-yu. Research on the behavior of fluid flow in a single fracture and its equivalent hydraulic aperture[J]. Advances in Water Science,2002,13(1): 61-67.
[8]BARTON N. Rock Joints[M]. Rotterdam: A. A. Balkema Publishers,1990.
