基坑开挖对邻近地下管线影响的变形控制标准

张陈蓉，俞 剑，黄茂松

（1.同济大学 地下建筑与工程系，上海 200092；2.同济大学 岩土及地下工程教育部重点实验室，上海 200092)

1 引 言

随着城市的发展，建筑用地日趋紧张，基坑开挖对周边环境的影响问题显得日益突出。基坑开挖不可避免地会造成周围的地层扰动，从而引起邻近管线的附加位移和受力，严重的甚至会引起管线的开裂破坏等。作为城市生命线工程的地下通讯线缆、高压供电电缆、城市给排水管网、煤气管道等错综复杂的地埋管网，其隐蔽性导致安全问题难以被监测，而一旦出现断裂，后果不堪设想。为此，城市区域的基坑控制标准变得尤为苛刻，必须在满足自身强度要求的基础上进而实现对周边扰动土体的变形控制，以满足邻近区域地埋管线的安全正常使用。

基坑开挖对邻近管线的影响分析是一个涉及基坑、土体、管线相互作用的整体三维问题。现有的研究一般分为两类，一类是采用有限元数值分析方法进行整体建模以实现基坑的实际开挖施工过程，如Ahmed等[1]分别采用二维、三维有限元模拟了深沟渠的开挖对邻近铸铁管线的影响。李大勇等[2]采用三维有限元方法分析了内撑式基坑工程开挖对地下管线的影响规律。此类基于受力控制的整体有限元分析方法（FCFEM）可以模拟整个施工工况，但对有限元建模要求高、工作量大、且针对性过强，很难在初期给予设计人员迅速有效地建议。其二是位移控制分析方法，此类方法不关注细节的基坑开挖施工过程，直接将基坑开挖引起的自由土体位移场作为外界控制条件，用以分析管线的受力和变形，规避了基坑的实际开挖过程模拟这一繁琐且针对性过强的因素。位移控制分析方法过程简单、物理意义明确，与基坑环境影响的变形控制标准理念一致，更适应工程界的需求。该方法分为位移控制有限元方法（DCFEM）和位移控制两阶段简化分析方法两类。DCFEM 方法通过在应力自由面施加位移边界条件来模拟基坑开挖引起的应力释放，亦即在基坑开挖临空面和坑外地表施加位移边界条件。而两阶段法是将管线模拟为弹性地基梁，将管线位置处的自由土体位移直接施加于管线上进行分析。蔡建鹏等[3]采用二维 DCFEM 法进行了基坑开挖对邻近地下管线的影响分析，并与整体有限元结果做了对比。笔者[4]在此基础上进一步提出了三维的 DCFEM 法和位移控制两阶段简化分析方法。

至于基坑环境影响的变形控制标准的提出，是伴随着城市基坑建筑用地的苛刻条件而出现的一个新兴课题，最新版的《上海市基坑工程技术规范》[5]基于周边待保护建（构）筑物的重要程度以及距离基坑远近等因素提出了基坑环境保护等级一级、二级、三级的概念，限定了围护墙的最大侧移以及基坑外地表最大沉降与基坑开挖深度的关系。该规范对于环境保护等级的定义比较模糊，并且只是绝对地根据保护等级将开挖深度与围护墙体变形、地表沉降建立线性的关系，另外没有考虑地埋管线自身承受能力的差异，因此，仍然有进一步修正的空间和必要。

基于以上需求，本文在分析上海软土地区板式支护体系基坑周边土体变形规律的基础上，采用位移控制两阶段简化方法，基于市政管线的自身承受能力，提出了基坑开挖对周边管线保护的基坑变形控制标准，以期为基坑开挖环境影响评价标准的建设提供相应的理论依据。

2 位移控制两阶段简化分析方法

两阶段法将基坑开挖对管线的影响分成两个阶段：第1阶段分析开挖引起的管线位置处的自由土体位移；第2阶段基于Winkler地基模型，将上述自由土体位移作为外界条件施加于管线上，分析管线的相应变形和内力。该方法关键是要得到合乎实际的管线位置处自由土体位移。

2.1 基坑开挖引起的自由土体位移场

基坑开挖引起的自由土体位移场计算方法有经验法、有限元法和解析法3种。目前研究多集中在围护墙的侧向变形和地表沉降曲线上，由于实测数据稀少，土层内部土体变形规律相关结论很少。本文在前人工作的基础上，结合上海软黏土地区若干基坑工程实例，针对采用板式围护结构体系的基坑工程，提出了三维围护墙体的侧向变形曲线以及地表沉降预测公式，然后简要介绍了采用DCFEM方法得到的基坑附近土体沉降沿深度的变化规律和土体侧向变形沿距离基坑远近水平方向的变化规律。图1为基坑围护墙的侧向变形及基坑外地表沉降示意图。定义x轴方向为沿基坑的横向，y轴方向为沿基坑的纵向，亦即管线的延伸方向。

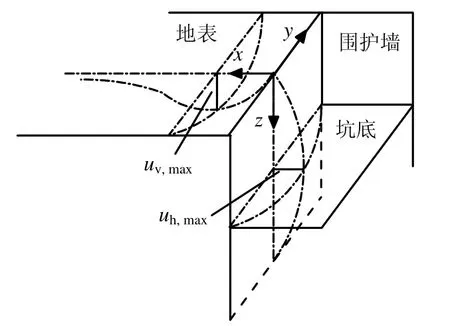
图1 基坑围护墙变形及地表沉降示意图Fig.1 Diagram for deformation of excavation and ground settlement

2.1.1 地表沉降曲线

对于基坑长度范围内坑外横向地表沉降预测曲线，采用Hsieh和Ou[6]的预测曲线公式如下：

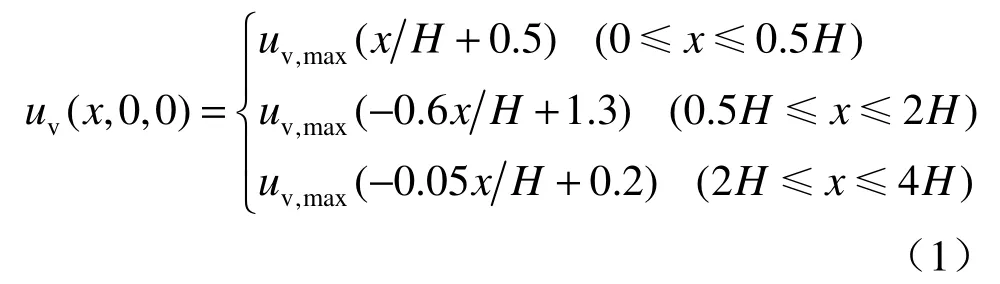
式中：uv,max为地表最大沉降量；基坑开挖深度H。由该式可知，沿x轴方向坑外地表沉降为凹槽形，最大沉降为0.5H处，4H范围外地表沉降近似为0。图2显示该预测公式与上海市板式支护体系坑外地表沉降规律较为吻合。

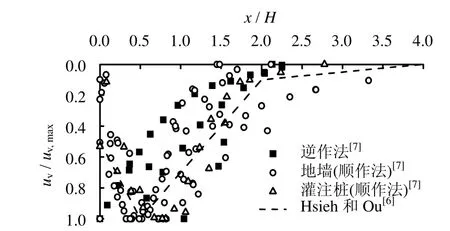
图2 相对地表沉降与相对围护墙距离关系Fig.2 Relationships between ground settlement normalized by maximum settlement and normalized distance from wall

同时笔者[4]在文献[8－10]的基础上，进一步提出了基坑纵向范围内坑外地表沉降的预测公式如下：

式中：A为变形影响半径，与基坑的开挖深度H、基坑纵向长度L有关。

由式（2）可知，沿y轴方向地表沉降沿基坑对称面呈正态分布，在距离基坑开挖对称面A处（即y=A）沉降仅为对称面处（即y=0）沉降的0.05。图3为基坑外地表沉降示意图。

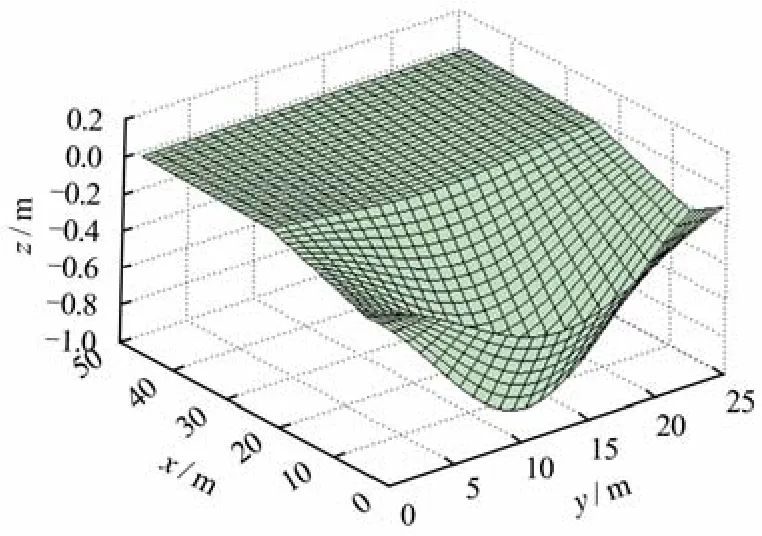
图3 基坑外地表沉降分布Fig.3 Settlement distribution for ground around foundation pit

2.1.2 基坑围护墙的水平向变形预测曲线

由上海若干典型基坑工程围护结构侧向变形实测数据，本文总结了其变形规律，得到基坑对称面上围护墙的侧向变形公式为

式中：uh,max为围护墙的最大侧向位移。

由式（4）可知，沿z轴方向围护墙的最大侧向变形位于基坑坑底处，与Ou等[11]的结论一致，墙顶位移约为最大位移值的 1/5。图 4为上海地区 4个基坑工程围护墙的实测数据与拟合公式的对比，可以看出，整体还是比较吻合的。

Roboski和Finno[9]进一步认为，板式围护基坑地表纵向沉降形态与围护墙沿纵向的侧向变形形态一致。由此，本文提出了基坑围护墙侧向变形预测公式为

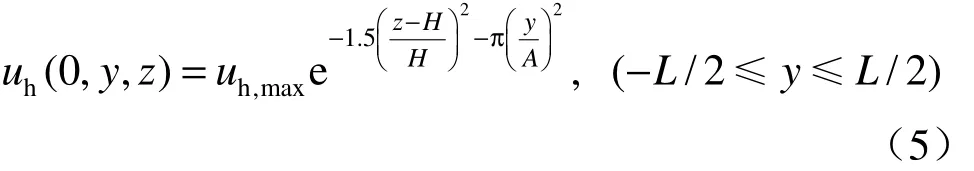
由式（5）可知，沿y轴方向，围护墙的最大侧向位移沿基坑对称面呈正态分布，在距离基坑开挖对称面A处（即y=A）侧向变形仅为对称面处（即y=0）侧向变形的0.05。图5为基坑围护墙侧变形示意图。

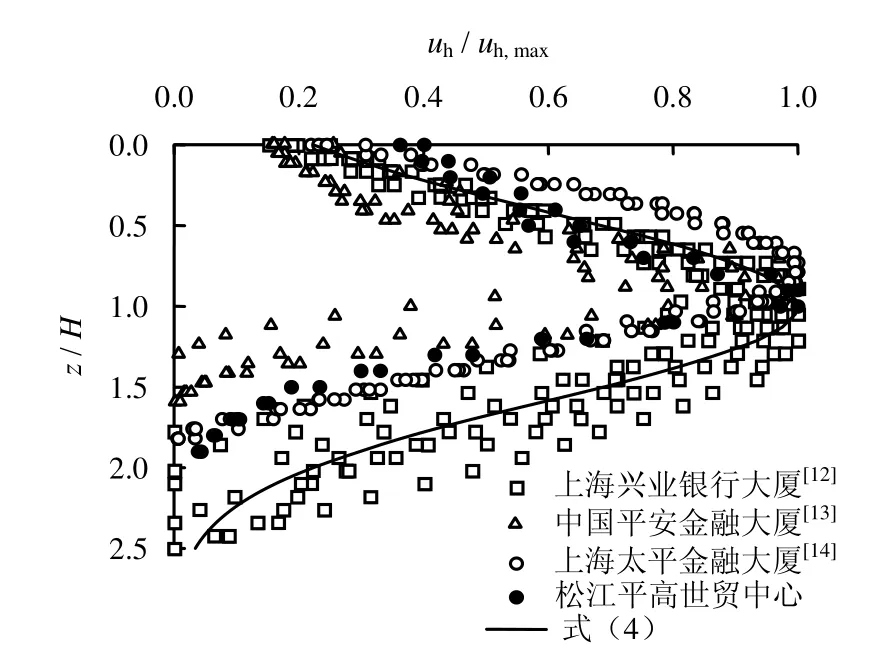
图4 相对围护墙侧向变形与开挖深度关系Fig.4 Relationships between normalized lateral displacement of wall and excavation depth

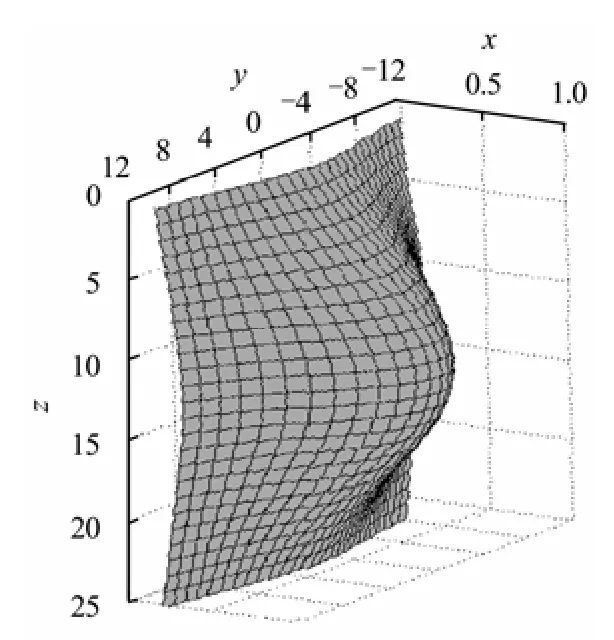
图5 基坑围护墙侧向位移分布Fig.5 Lateral displacement distribution of wall for excavation pit

2.1.3 土体沉降沿深度变化规律

一般的地埋管线埋深在0～6 m范围内，可近似地认为，地表以下0～6 m范围内土体的纵向沉降形态与地表纵向沉降形态一致。将上述基坑开挖应力自由面的位移作为边界条件，采用笔者提出的DCFEM法[4]，对基坑外土体沉降沿深度的变化规律进行了探讨，由拟合结果得到上海软黏土地区板式围护基坑体系坑外土体沉降沿深度的衰减变化规律如下：

由式（6）可知，距离基坑开挖面0.5H范围内，土体沉降沿深度呈指数衰减（见图 6），在0.5H～1.5H以及1.5H以外各自呈线性衰减。

图6 基坑外土体沉降沿深度衰减（0 < x ≤ 0.5H）Fig.6 Attenuation of settlement with depth

2.1.4 土体侧向变形沿水平方向的变化规律

采用上述同样方法，本文得到上海软黏土地区板式围护基坑体系坑外土体侧向变形沿距离基坑远近水平方向的衰减变化规律如下：

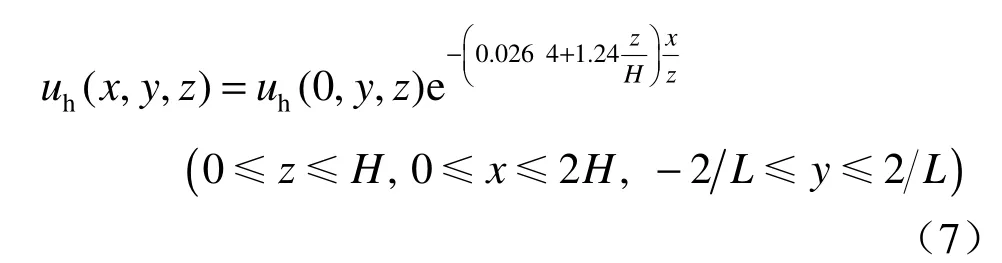
式（7）表明，在基坑开挖的纵向和深度范围内，同一深度处土体侧向变形沿水平方向呈指数衰减，见图7。

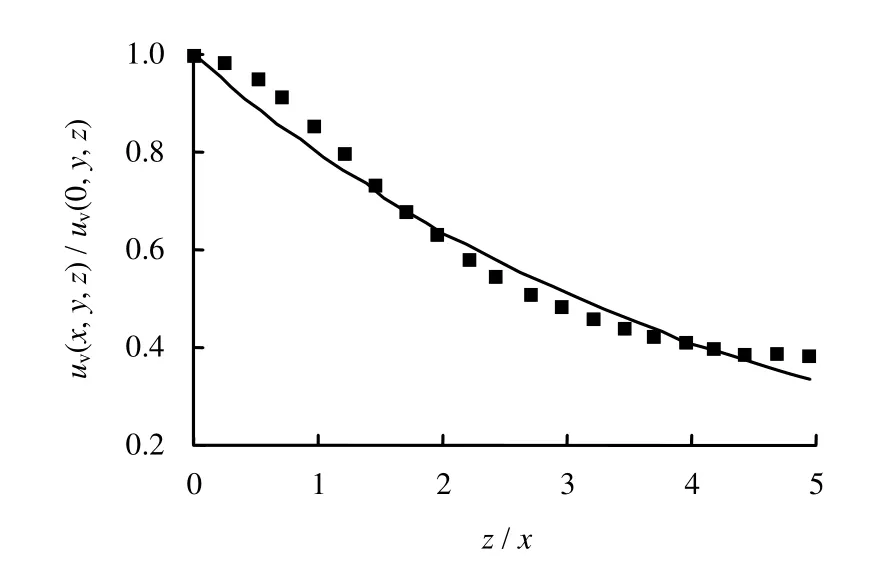
图7 基坑外土体侧向变形沿水平方向衰减（z=0.4 m）Fig.7 Attenuation of horizontal deformation with distance

2.2 简化分析方法的验证

所采用的计算模型如下：基坑平面尺寸为30 m×30 m，开挖深度为10 m。土体为均质土层，采用线弹性模型，重度为16.8 kN/m3，变形模量为2.124 MPa，泊松比为0.4。地下管线中心埋深2 m，距离开挖面远近2 m，管线长为30 m。管的外径为0.635 m，壁厚为0.01 m，弹性模量为150 MPa，泊松比为0.2，每截管长为5 m，如图8所示。

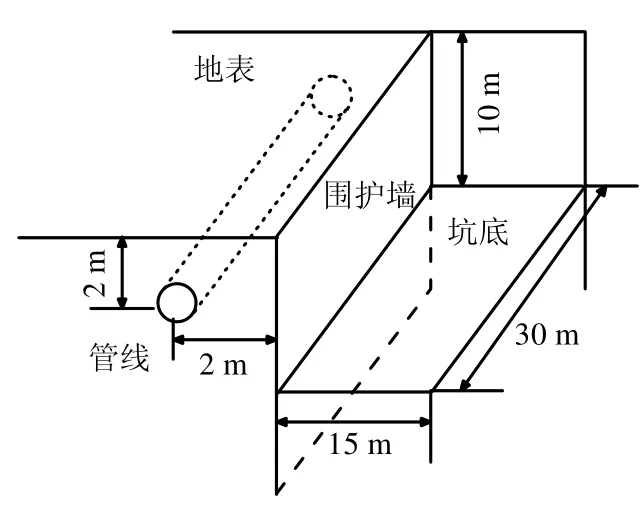
图8 基坑算例示意图（一半基坑）Fig.8 Case study of foundation pit

将均质地基条件下的两阶段简化方法分析结果与位移控制有限元法分析结果进行了对比。图 9、10为刚性接口管线的位移和弯矩沿管线纵向分布图，图11、12为柔性接口管线的位移和弯矩沿管线纵向分布图（柔性接口管线主要关注其变形）。两种方法计算得到的刚性、柔性管线受力变形图均比较接近，管线的位移和弯矩关于基坑开挖面对称。对刚性接口管线而言，两阶段法得到的位移弯矩最大值均比DCFEM结果偏小，而柔性接口管线两种方法结果更为吻合。另外，各自比较刚、柔性接口管线的位移图和弯矩图发现，刚性接口管线的最大位移要比柔性接口管线小，而由于柔性接口管线接口处不传递弯矩，其整体弯矩要比刚性接口管线小很多。

在此必须认识到计算结果的吻合与两种方法同属于位移控制分析方法有关，同时也进一步证实了针对地埋管线这种结构形式不是很复杂的构筑物，两阶段简化分析方法完全可以替代有限元的工作，且计算结果分析迅速，参数分析物理意义明确，对工程界有实际的指导意义。

3 基于管线承受能力的基坑变形控制标准

3.1 管线自身抵抗变形的能力

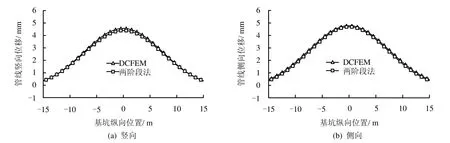
图9 刚性接口管线变形图Fig.9 Deformations for rigid pipeline

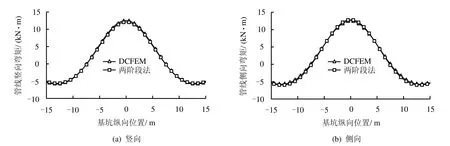
图10 刚性接口管线弯矩图Fig.10 Bending moment diagrams for rigid pipeline

图11 柔性接口管线变形图Fig.11 Deformations for flexibility pipeline

图12 柔性接口管线弯矩图Fig.12 Bending moment diagrams for flexibility pipeline

城市区域地埋管线包括给排水、煤气、通讯电缆等各种用途的管线。现有的相关行业规范、国家标准都对各类管线的材料性能给出了相应的破坏标准。总体来讲，刚性接口管线对管线纵向应力，柔性接口管线对接口相对转角给出了各自限制。但这些标准都是针对管线的生产加工质量而言，此时管线内部无使用压力，管线外部没有土体压力、车辆荷载等实际外部荷载，没有考虑铺设时管线的初始变形以及使用期间管线的长期沉降、管线自身老化等外界因素，仅是针对材料本身的破坏标准。对于长期埋置于地下的管道，上述破坏标准过于宽松，并不适用。从基坑开挖环境保护角度分析，本文对前人的相关工作进行了总结对比，尝试性地对管线自身抵抗变形能力限定了一个标准，见表1。

表1 管线抵抗变形承受能力比较Table1 Comparison of bearing capacity for pipelines

分析表1发现，对于环境保护的管线整体上允许倾斜角度控制在0.034°～0.172°之间，国内标准限定在 0.114°～0.172°范围，德国标准限定在0.057°～0.114°范围。综合我国实际情况和国外标准，在此建议以0.1°作为环境保护中管线附加变形的承受能力控制标准。

3.2 现有变形控制标准的验算

最新版的《上海市基坑工程技术规范》[5]给出的基坑变形设计控制指标见表2。

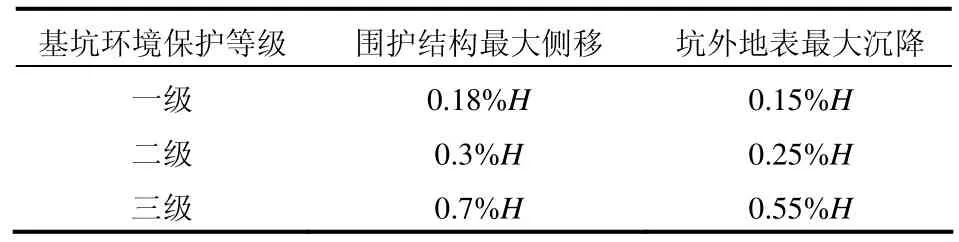
表2 基坑变形控制指标Table2 Deformation controlling criteria for excavation pit

根据规范给出的各级环境保护等级下基坑围护墙体和坑外土体的位移最大限值，采用位移控制两阶段分析方法分别对一典型基坑开挖附近的刚性管线和柔性管线进行分析。

算例：除基坑开挖深度为3～30 m以外，其余均与2.2节均质地基算例相同。

分别针对刚性和柔性管线在一、二、三级环境保护等级下，基坑开挖深度为3、5、10、15、20、25、30 m 的情况，分析得到了距离基坑水平位置2 m的管线的最大倾斜值，具体结果见图13。

由图13可知，随着基坑开挖深度的增加，管线的倾斜角度也相应增加。一级环境保护对土体变形要求最严，刚性接口管线在算例所示的开挖深度内没有超出管线的承受能力标准0.1°，而柔性接口管线在开挖30 m时才超出管线的承受能力标准。而随着开挖深度的增加，二级保护等级下开挖 10 m时、三级保护等级下开挖5 m时管线均超出了其承受能力标准。由此可见，现有的上海市基坑工程技术规范提供的基坑变形控制指标作为一个对基坑变形的绝对控制量，没有考虑管线的承受能力标准，不能反映随着基坑开挖深度的增加、管线变形增加，从而对基坑开挖应给予的约束。另外本算例只是考虑了基坑开挖深度的变化，例如管线的埋置深度、管线距离基坑远近等因素均没有考虑。而基坑环境保护等级的概念也较为模糊，实际操作受主观因素影响较大。

图13 基坑开挖深度与地埋管线倾角关系图Fig.13 Relationships between excavation depth and angle for pipeline

3.3 基坑开挖邻近管线保护变形控制标准的提出

针对以上不足，本文尝试性地从管线变形承受能力角度出发，针对上述基坑条件，对每一开挖深度改变围护结构的最大水平位移，得到围护结构的最大变形与管线的倾斜角度关系，以获得每一基坑开挖深度下基于管线承受能力的临界围护结构侧移。分别计算了管线与基坑距离2、3、4 m的情况。具体结果见图14。

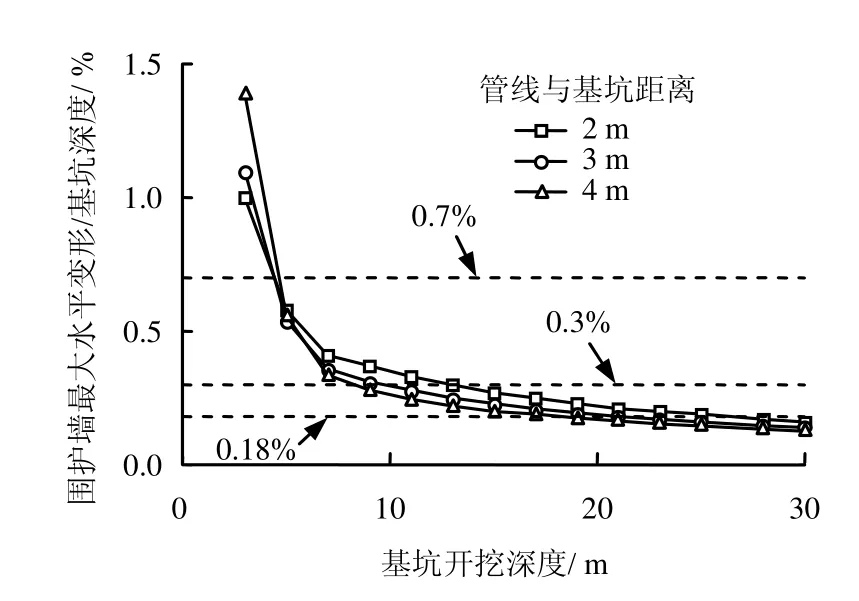
图14 基坑开挖深度与围护墙侧向变形关系图Fig.14 Relationships between excavation depth and deformation for retaining wall

由图14可知，随着基坑开挖深度的增加，在开挖较浅时（5 m范围内），距离基坑越远的管线所对应的围护墙侧向变形越大，而随着开挖深度增加（大于5m），则距离基坑越近的管线所对应的围护墙侧向变形越大。首先由1.3节的算例分析可知，管线的竖向变形和侧向变形相差不大，在此围护墙的最大侧向变形以受管线竖向变形控制。其次土体的沉降是凹槽形，在距离基坑0.5H时达到最大。在基坑开挖较浅时，距离基坑越近处自由土体位移越大，在凹槽形的右边。而随着基坑开挖深度增加，距离基坑越近处自由土体位移越小，在凹槽形左边。土体位移越大，管线相应的变形受力也越大。上述规律是与管线所处土体沉降区域有关的。图14中同时给出了现有的针对各级环境保护等级的基坑变形控制指标，可以看出，该指标没有考虑管线的承受变形能力，物理意义不甚明确。本图仅是针对一典型算例给出的管线保护对应的基坑变形控制指标。现实中土体条件，管线条件以及各管线的自身承受能力差异等，该算例还不足以覆盖所有的情况。在此，文中仅是对基坑环境保护标准建设提供了一定的理论依据，到具体的实现还有相当的计算工作量和实际算例的验证。

4 结 论

（1）基于工程实例，提出了上海软黏土地区基坑工程周围土体沉降规律和围护墙变形规律，并采用位移控制有限元分析方法，得到了基坑外土体内部变形规律。

（2）分别对均质地基中刚、柔性管线以及非均质地基中刚性管线，通过与DCFEM法的比较，验证了作者提出的简化分析方法的合理性。

（3）从管线自身承受能力角度提出了基坑开挖对管线保护的变形控制指标。可以认为，随着开挖深度的增加，基于对管线的保护，围护墙的变形与开挖深度比值越来越小。而同一开挖深度，对不同水平距离的管线，其变形控制要求的大小与管线处于土体沉降区域有关。与现有的上海市基坑工程技术规范的对比，以说明本文对基坑变形控制标准理念的改进。通过本文的工作，希望可以为基坑开挖环境影响评价标准的建设提供相应的理论依据。

[1]AHMED I. Pipeline response to excavation-induced ground movements[D]. New York,Cornell University,1990.

[2]李大勇,吕爱钟,曾庆军. 内撑式基坑工程周围地下管线的性状分析[J]. 岩石力学与工程学报,2004,23(4):682－687.LI Da-yong,LÜ Ai-zhong,ZENG Qing-jun. Behavior analysis of buried pipeline response to nearby excavation pit with braced retaining structure[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(4): 682－687.

[3]蔡建鹏,黄茂松,钱建固,等. 基坑开挖对邻近地下管线影响分析的 DCFEM 法[J]. 地下空间与工程学报,2010,6(1): 120－124.CAI Jian-peng,HUANG Mao-song,QIAN Jian-gu,et al.DCFEM method for analyzing the influence of deep excavation on adjacent underground pipelines[J]. Chinese Journal of Underground Space and Engineering,2010,6(1): 120－124.

[4]张陈蓉,蔡建鹏,黄茂松. 基坑开挖对邻近管线的影响分析[J]. 岩土工程学报,2010,32(增刊2): 154－157.ZHANG Chen-rong,CAI Jian-peng,HUANG Mao-song.Influence of deep excavation on adjacent underground pipelines[J]. Chinese Journal of Geotechnical Engineering,2010,32(Supp.2): 154－157.

[5]上海市勘察设计行业协会. DG/TJ08－61－2010 上海市基坑工程技术规范[S]. 上海: [s. n.],2010.

[6]HSIEH P G,OU C Y. Shape of ground surface settlement profiles caused by excavation[J]. Canadian Geotechnical Journal,1998,35(6): 1004－1017.

[7]WANG J H,XU Z H,WANG W D. Wall and ground movements due to deep excavations in Shanghai soft soils[J]. Journal of Geotechnical and Geoenviromental Engineering,ASCE,2010,136(7): 985－994.

[8]唐孟雄,赵锡宏. 深基坑周围地表任意点移动变形计算及应用[J]. 同济大学学报,1996,24(3): 238－244.TANG Meng-xiong,ZHAO Xi-hong. Ground settlement and deformation calculation and application in deep excavation[J]. Journal of Tongji University,1996,24(3):238－244.

[9]ROBOSKI J F,FINNO R J. Distributions of ground movements parallel to deep excavation in clay[J].Canadian Geotechnical Journal,2006,43(1): 43－58.

[10]FINNO R J,ROBOSKI J F. Three-dimensional responses of a tied-back excavation through clay[J]. Journal of Geotechnical and Geoenviromental Engineering,ASCE,2005,131(3): 273－282.

[11]OU C Y,LIAO J T,LIN H D. Performance of diaphragm wall constructed using top-down method[J]. Journal of Geotechnical and Geoenviromental Engineering,ASCE,1998,124(9): 798－808.

[12]戴斌,王卫东,徐中华. 密集建筑区域中深基坑全逆作法的设计与实践[J]. 地下空间与工程学报,2005,1(4):579－583.DAI Bin,WANG Wei-dong,XU Zhong-hua. Design &practice of deep foundation pit constructed by top-down method in dense-constructed area[J]. Chinese Journal of Underground Space and Engineering,2005,1(4): 579－583.

[13]龚晓南. 基坑工程实例2[M]. 北京: 中国建筑工业出版社,2008.

[14]黄炳德,翁其平,王卫东. 某大厦深基坑工程的设计与实践[J]. 岩土工程学报,2010,32(增刊1): 363－369.HUANG Bing-de，WENG Qi-ping，WANG Wei-dong.Design and application of deep foundation pit of a project[J]. Chinese Journal of Geotechnical Engineering,2010,32(Supp.1): 363－369.

[15]刘月梅. 城市施工中地下管线的保护[J]. 市政技术,2005,23(4): 235－236.LIU Yue-mei. Protection for buried pipeline from urban construction[J]. Municipal Engineering Technology,2005,23(4): 235－236.

[16]广州市建筑科学研究院. GJB02－98 广州地区建筑基坑支护技术规定[S]. 广州: [s. n.],1998.

[17]骆建军,张顶立,王梦恕,等. 地铁施工对管线的影响[J].中国铁道科学,2006,27(6): 124－128.LUO Jian-jun,ZHANG Ding-li,WANG Meng-shu,et al.Influence of metro construction on underground pipeline[J]. China Railway Science,2006,27(6): 124－128.