通过测斜数据预判测斜管失效的分析方法研究

刘 欣，雷国辉，张坤勇，艾英钵，施建勇

（1. 河海大学 岩土力学与堤坝工程教育部重点实验室,南京 210098; 2. 河海大学 岩土工程科学研究所,南京 210098）

1 引 言

岩土测斜仪广泛应用于道路、基坑、边坡等填方和挖方工程现场土体或结构物的位移监测。传统的岩土测斜仪系统主要由测斜探头、带导槽的测斜管、带刻度的电缆以及数据采集和存储装置组成[1]。测斜探头属精密仪器，如常用的伺服加速度计式测斜探头的分辨率可高达0.02 mm/500 mm。关于测斜仪系统的应用研究目前主要集中于测量误差和精度的分析以及测量数据的处理方法[2－4]，然而，实际应用时，尤其是在边坡滑移变形监测项目中[5－6]，经常会遭遇由于测斜管局部变形过大，导致测斜探头难以下放，或者偶然下放后却难以上提的棘手问题，不仅致使测斜管报废，甚至直接致使测斜探头报废，影响后续监测工作，造成数据缺失和经济损失。测斜管局部变形过大的时刻往往是影响监测对象的稳定性和安全性最为关键的时刻，因此，有必要通过分析测量数据预判测斜管失效的可能性，以便及时采取必要措施避免由此造成的损失。

2 测斜管失效判别原理

关于测斜管失效判别方法的文献并不多见。李积胜[6]对测斜管的失效判据进行过分析，通过图 1所示的测斜探头与测斜管之间的几何关系，推导出测斜管失效时极限曲率半径Rmin与探头和电缆刚性接头的总长度l、测斜管内径dc以及探头直径dp之间的表达式：

相应的极限曲率的表达式为

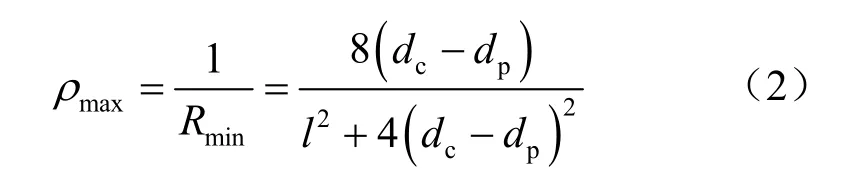
以及测斜管失效时对应的极限折角为

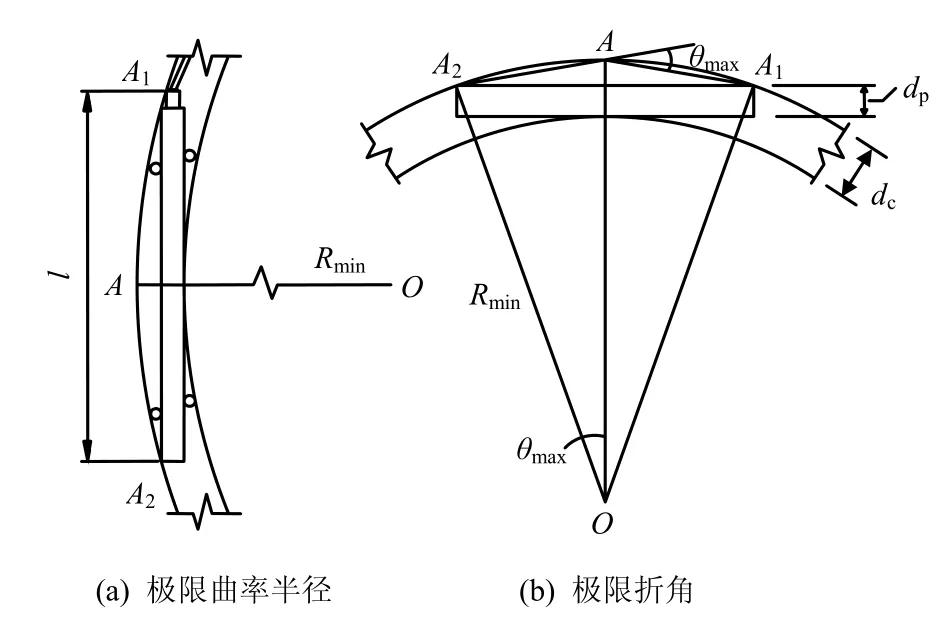
图1 测斜管失效时探头与管的几何关系[6]Fig.1 Geometrical relationship between inclinometer probe and casing upon failure of the casing[6]

为分析测斜管变形过程中各测点的曲率半径，他还提出如图2所示的三型值点双圆弧插值方法，针对测斜管局部任意3个连续测点p1、p和p2的测斜数据，采用两段圆弧分别对相邻两个测点的测斜数据进行插值，并依据在中心测点位置两圆弧切线相同的约束条件，建立了确定双圆弧曲率半径的计算方法，取双圆弧曲率半径的小值与式（1）的极限曲率半径进行对比，评判测斜管失效的可能性，然而以下分析显示，实际上图2的三型值点双圆弧插值方法并不适用于测斜管局部变形曲线的分析。

图2 三型值点双圆弧插值法示意图[6]Fig.2 Sketch of biarc interpolation of three data points[6]

测斜仪系统直接测量得到的数据是各测点位置测斜管导槽平面（而非探头轴线）[2]与重力铅垂线的夹角δi。传统上，测斜数据通常被处理为测点的位置比如深度zi和对应的位移xi值，深度zi一般是简单地取为测距L（通常为500 mm）的整数倍，位移 xi值一般是从管底起算、取测斜管的相对位移值，即土体或结构物等监测对象变形后与变形前初值之间的差值，以反映监测对象的位移响应。事实上，测斜管在埋设时，并不能保证其是铅直的，放入测斜管内的测斜探头以及与其连接的电缆线的长度并不代表测点的真实深度。因此，采用曲率半径、曲率或折角的方法评判测斜管失效的可能性时，测斜数据应采用测斜管内各测点的真实深度和绝对位移值，如图3所示，从管底测点起算其计算公式应为

式中：N为测斜管从管底测点起算的总测点数，i =2，3，…，N。

图2中在采用局部任意3个连续测点p1、p和p2的测斜数据进行双圆弧插值时，认为相邻两测点p1p和 pp2的线段长度不等，而 p1p2的线段长度取为2倍的测距。但是，测斜仪系统的测试原理就已表明，相邻两测点的线段长度都代表了测距 L，二者应该是相等的，中心测点p本身就应该在与其相邻的两端测点p1和p2的中垂线上，自然满足在中心测点位置两圆弧切线相同的约束条件，且两圆弧的曲率半径也相等。因此，所谓的三型值点双圆弧插值方法实际上应该是三型值点圆弧插值方法。

为分析测斜管变形曲线的曲率变化，并且考虑满足变形曲线的光滑性以及失效时大挠度变形的保凸性要求，本文利用测斜数据处理公式（4），提出基于三型值点的圆弧插值法、四型值点的三次多项式插值法和双圆弧插值法以及五型值点的单点约束拟合双圆弧法，分别推求测斜管各测点对应的曲率，与极限曲率公式（2）进行对比，评判测斜管失效的可能性，同时也提出比较简单的基于两型值点的折角比较法，与极限折角公式（3）进行对比，评判测斜管失效的可能性。另外，将所提出的方法运用于某地铁车站基坑工程现场施工监测过程中1根测斜管的失效实例，对比分析了各方法的适用性。

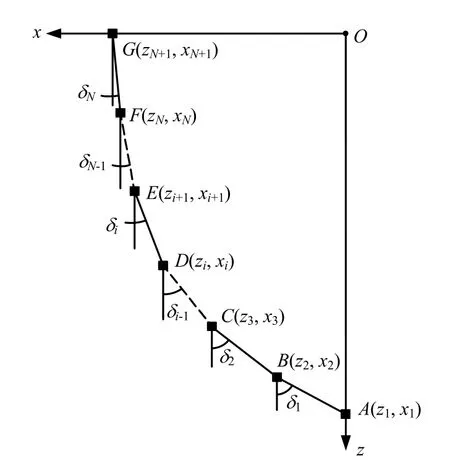
图3 测斜数据分析实际深度和绝对水平位移示意图Fig.3 Sketch of analyzing the true depths and absolute horizontal displacements using the inclinometer data

3 计算方法

3.1 曲率计算公式

运用测斜数据分析结构物的弯矩响应，比如分析地下连续墙或桩墙支护结构的弯矩响应或者分析水平荷载作用下桩基的弯矩响应时，通常是按照小挠度变形问题，采用下面的近似公式，计算监测对象变形响应曲线的曲率[7]：

对于由局部变形过大导致的测斜管失效问题，小挠度变形已不再适用，严格的曲率计算公式[7]为

3.2 三型值点圆弧插值法

三型值点圆弧插值法是能够满足测斜管局部变形曲线光滑性的一种最简单方法。对于图4所示任意 3个连续测点 pi-1(zi-1,xi-1)、pi(zi,xi)和 pi+1(zi+1,xi+1)，由于相邻两个测点 pi-1pi和 pipi+1的线段长度都等于测距 L，对三角形 pi-1pipi+1运用余弦定理可得

式中：α、Ri的符号意义见图4。

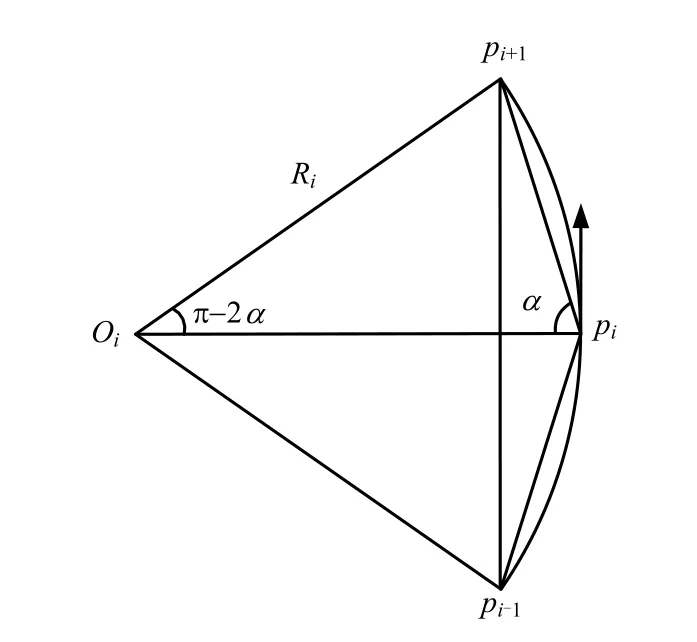
图4 三型值点圆弧插值法示意图Fig.4 Sketch of three data points arc interpolation

3.3 四型值点三次多项式插值法

针对局部测点的测斜数据，采用三次多项式插值法确定其对应的曲率半径是最直观的方法。设三次多项式为

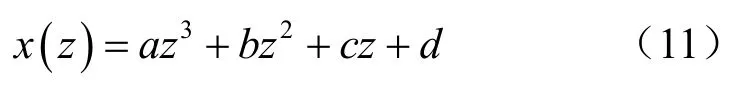
式中：a、b、c、d分别为待定系数。因此，该多项式需要4个测点的测斜数据来确定。设局部任意4个连续测点及其测斜数据为 pi-2(zi-2,xi-2)、pi-1(zi-1,xi-1)、pi(zi,xi)和pi+1(zi+1,xi+1)，代入式（11）则构成四元一次方程组：

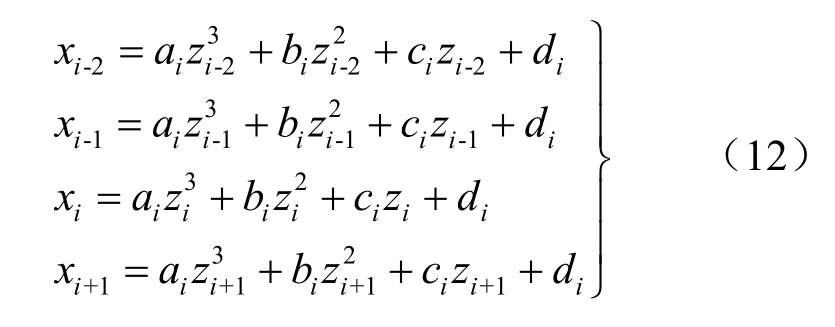
利用数学软件 MATLAB可以方便地求解出式（12）中的待定系数，代入式（11），并对z分别求一阶和二阶导数后代入式（6）可得测点 pi处的曲率为

3.4 四型值点双圆弧插值法

双圆弧插值法除了能够使得所构成的圆弧段之间保持一阶光滑外，还具有较好的保凸性[8]，与上述插值法相比，更适合于大挠度变形曲线的插值[9]。该方法采用两段圆弧对测斜管变形曲线上局部4个连续测点的数据进行插值。如图5所示，设局部任意4个连续测点及其测斜数据为pi-2(zi-2,xi-2)、pi-1(zi-1,xi-1)、pi(zi,xi)和 pi+1(zi+1,xi+1)。第一段圆弧针对测点pi-2、pi-1和pi采用前述三型值点圆弧插值法确定，第二段圆弧针对测点pi和pi+1构造且满足两段圆弧在交点pi处切线相同的约束条件。根据几何关系可以知道，第二段圆弧的圆心 Oi2必然在第一段圆弧的最近一条径线Oi1pi或其延长线上。最终，取两段圆弧的最大曲率作为双圆弧交点 pi处的曲率。

图5 四型值点双圆弧插值法示意图Fig.5 Sketch of biarc interpolation method of four data points

对于由测点pi-2、pi-1和pi构造的第一段圆弧，按照前述三型值点圆弧插值法即式（10）可以很容易地确定其曲率：

对于由测点pi和pi+1构造的第二段圆弧，可以采用平面解析几何方法，先确定两段圆弧的圆心坐标位置，再推求曲率半径和曲率。

第一段圆弧的圆心Oi1是线段pi-2pi-1和pi-1pi的中垂线的交点。线段pi-2pi-1和pi-1pi的中垂线方程为

式中：k1、k2分别为线段pi-2pi-1和pi-1pi中垂线的斜率；(zm1,xm1)和(zm2,xm2)分别为线段pi-2pi-1和pi-1pi中点的坐标，其表达式为

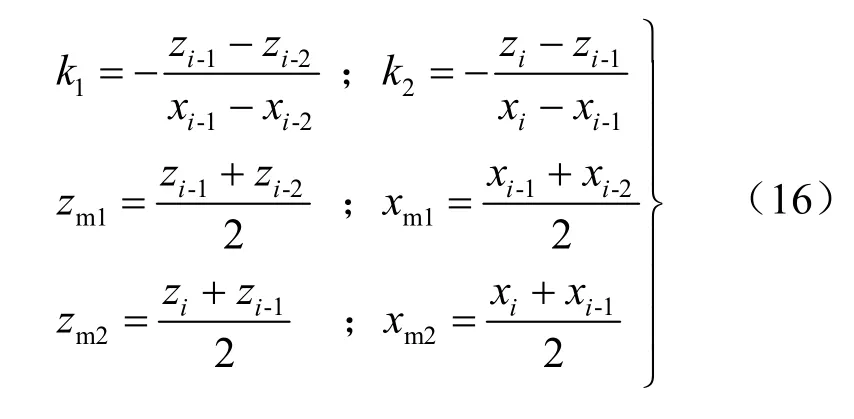
求解式（15）的联立方程组可得圆心 Oi1的坐标为

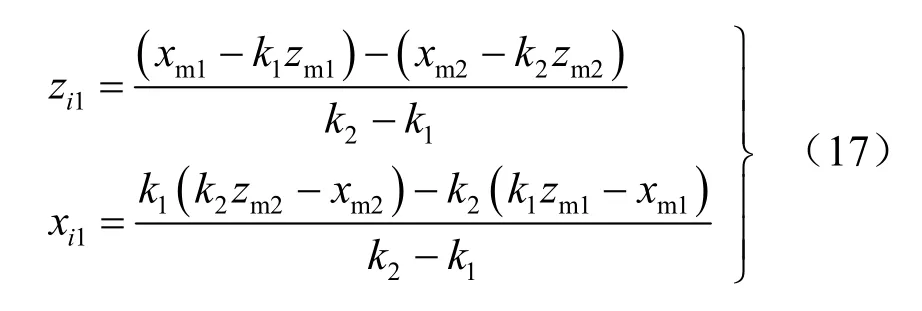
第二段圆弧的圆心Oi2是线段pipi+1的中垂线和过 Oi1和 pi直线的交点。线段 pipi+1的中垂线和过Oi1和pi的直线的方程为

式中：km、ki分别为线段 pipi+1的中垂线和过 Oi1pi直线的斜率；(zm,xm)为线段 pipi+1中点的坐标，其表达式为

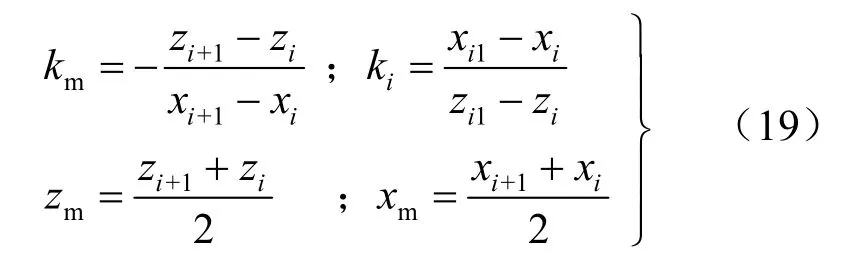
求解式（18）的联立方程组可得圆心 Oi2的坐标为

则第二段圆弧的曲率为

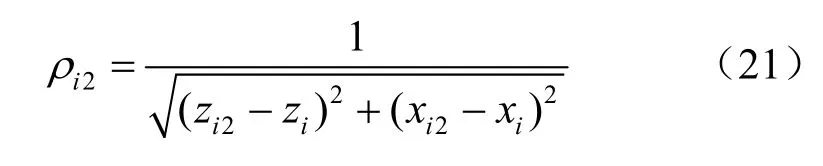
由式（14）和式（21）可得pi测点处的曲率：

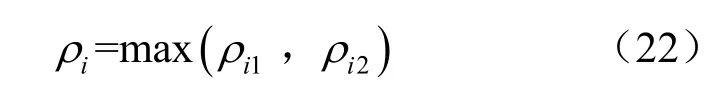
3.5 五型值点单点约束拟合双圆弧法

以上针对测斜管局部变形曲线所提出的插值法都要求各型值点即测点坐标满足插值函数或位于插值曲线之上。而拟合法则以逼近型值点为目标，建立相应的函数或曲线，为此本文也进行了这方面的尝试，在文献[10]的基础上，建立了基于五型值点的单点约束拟合双圆弧法。

如图6所示，设测斜管变形曲线上任意5个连续的测点及其测斜数据为pi-3(zi-3,xi-3)、pi-2(zi-2,xi-2)、pi-1(zi-1,xi-1)、pi(zi,xi)和 pi+1(zi+1,xi+1)，采用单点约束拟合法[10]首先利用pi-3、pi-2、pi-1和pi这4个测点的数据采用最小二乘法进行第一段圆弧拟合，且满足第4个测点pi在拟合圆弧上的约束条件。第二段圆弧针对测点pi和pi+1构造且满足两段圆弧在交点pi处切线相同的约束条件。最终，取两段圆弧的最大曲率作为双圆弧交点pi处的曲率。

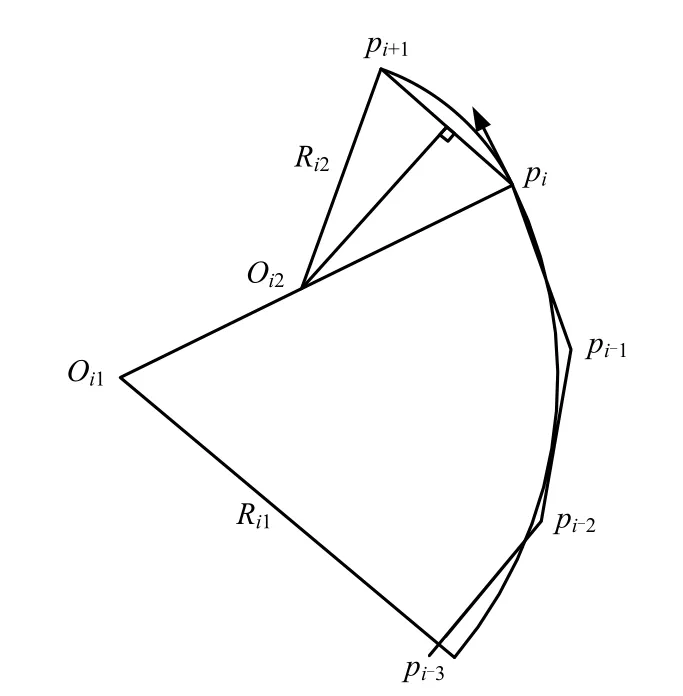
图6 五型值点单点约束拟合双圆弧法示意图Fig.6 Sketch of biarc fitting of five data points with an end point constraint

对于第一段圆弧，以测点pi(zi,xi)为约束点，定义目标函数和约束条件，求解其圆心坐标 Oi1(zi1,xi1)及其半径 Ri1。由最小二乘法确定的目标函数为：

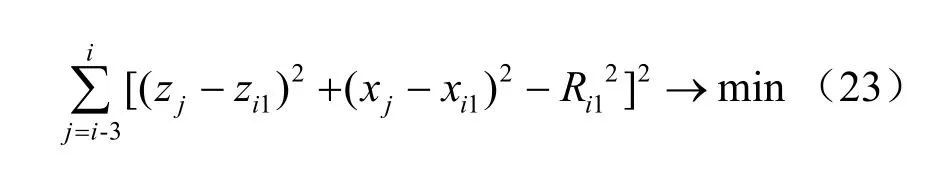
测点pi在拟合圆弧上的约束条件为

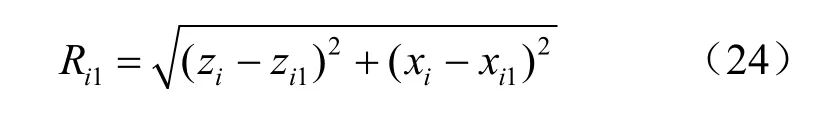
采用求极值的方法，将式（24）代入式（23），并令其分别对zi1和xi1求偏导后为0，可得[10]

将pi-3、pi-2、pi-1和pi测点的数据代入式（25）可得第一段圆弧的圆心坐标(zi1,xi1)，再代入式（24）可得其曲率半径，取其倒数则可得第一段圆弧的曲率 ρi1。

对于由测点pi和pi+1构造的第二段圆弧，则可以采用章节 3.4的方法，将式（25）得到的第一段圆弧的圆心坐标(zi1,xi1)代入式（19）～（21）得到其曲率 ρi2。

最后，根据式（22）取ρi1和ρi2的最大值得到pi测点处的曲率 ρi。

3.6 折角比较法

以上对于测斜管变形曲线的曲率分析方法相对比较复杂，本文也尝试提出最简单的，直接通过计算出相邻两测点的相对折角，与极限折角公式（3）对比，来评判测斜管失效的可能性。如图7所示，测点pi处的相对折角为

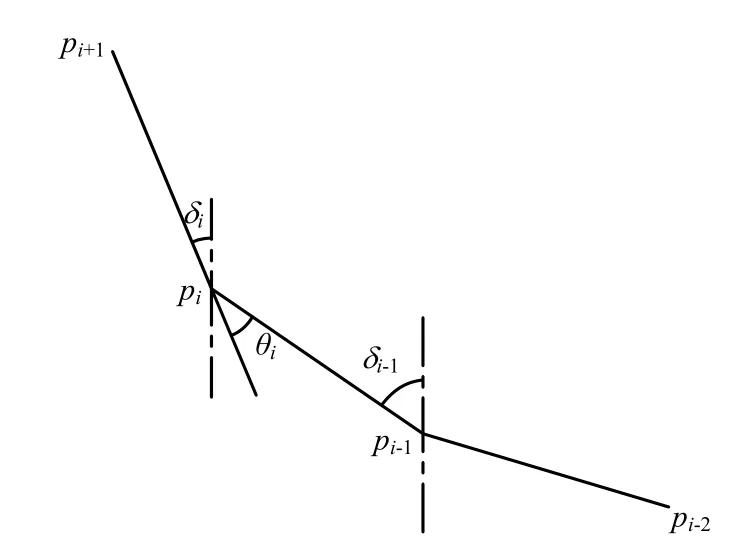
图7 折角比较法示意图Fig.7 Sketch of deflection angle comparison method

4 实例分析

某地铁车站基坑及测斜管位置平面图如图8所示，基坑主体长169.0 m，宽22.5 m，中间段挖深16.2 m，两端头盾构井挖深17.2 m，采用钢管支撑与SMW工法支护结构。现场施工监测在支护结构附近土层中共布置 9个测斜孔，监测工作从 2006年7月开始，至12月结束。期间，09号测斜管在9月8日实施监测时，测斜探头在测完深度10 m的数据后，在深度10.0～10.5 m段受阻，未能继续下放，并在10 m深度位置测得最大水平位移。同时，测斜管附近支护结构也发现局部渗漏险情，其原因在于附近临时堆土所致。随后通过堆土外运和堵漏措施解决，并重新钻孔埋设新的测斜管实施后续监测，但造成20 d数据缺失。当时若能通过测斜数据的分析提前预判测斜管的失效，或许可以避免数据缺失的问题。

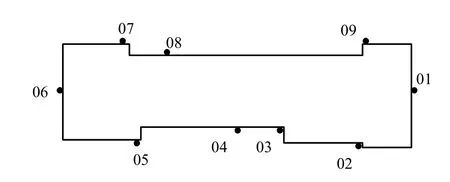
图8 测斜管布置平面图Fig.8 Plan of the arrangement of inclinometer casings

根据现场实测数据，采用式（4）的方法计算得到的09号测斜管8月31日至9月7日期间每日的绝对水平位移沿真实深度的变化曲线如图 9所示，其中位移值为负表示向着坑内的位移。由图可见，8 m至13 m深度位置的绝对水平位移变化最大，其曲率也日渐增大，是造成测斜管失效的危险部位。为检验本文所提出的测斜管失效判别方法的适用性，表1列出了深度5～15 m段的监测数据，并分别采用本文提出的5种方法，判别测斜管失效的可能性。

图9 09号测斜管绝对位移与深度曲线Fig.9 Absolute displacement-depth curve of No. 09 inclinometer casing

现场监测采用 CX－03型测斜仪和 PVC测斜管，测斜管外径为70 mm，内径dc=60 mm；测斜探头及其电缆刚性接头的总长l约为800 mm，探头直径为dp=32 mm。根据式（1）～（3）可算得测斜管失效时的极限曲率半径 Rmin=2.871 m，极限曲率ρmax=0.348，极限折角 θmax=8.008°。

针对表1的数据，分别采用三型值点圆弧插值法、三型值点三次多项式插值法、四型值点双圆弧插值法、五型值点单点约束拟合双圆弧法以及折角比较法计算得到的测斜管在 5～15 m 深度段各测点位置的曲率和折角如图10所示。由图可以看出，9月1日各深度测点的曲率和折角相对较小，但从9月3日开始，10 m深度上下测点的曲率和折角开始突然增大，并持续增大至9月7日达到最大值，其中三型值点圆弧插值法和三型值点三次多项式插值法计算得到的曲率值几乎相等，且都相对较小；四型值点双圆弧插值法计算得到的曲率值稍大；五型值点单点约束拟合双圆弧法计算得到的曲率值最大，与测斜管失效时的极限曲率值0.348相比，最接近于极限曲率。折角比较法的计算结果也显示出在深度10 m上下位置变化剧烈且最大折角逐日增加。

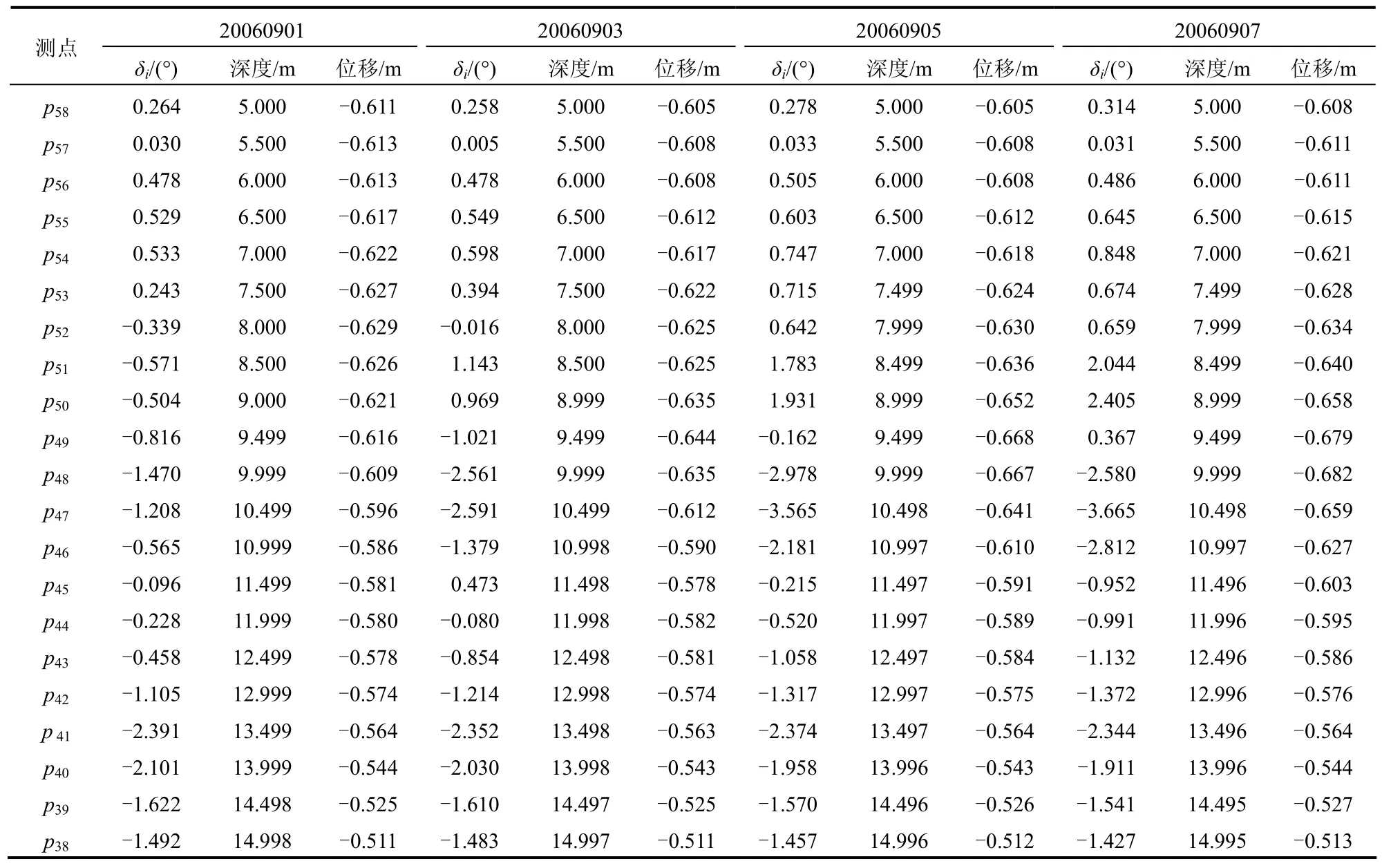
表1 09号测斜管局部深度的监测数据Table1 Measured data at local depths of No. 09 inclinometer casing

图10 5种测斜管失效判别方法计算结果对比Fig.10 Comparison of the calculated results by the five methods of detecting the failure of inclinometer casing

依据表1中9月7日的监测数据，5种方法计算得到的最大曲率或最大折角值、深度位置和由式（2）、（3）计算得到的测斜管失效时的极限曲率和极限折角值如表2所列。从表中可以看出，五型值点单点约束拟合双圆弧法计算得到的最大曲率值0.286与极限曲率值0.348最接近；四型值点双圆弧插值法计算得到的最大曲率值为0.155，约为0.45倍的极限曲率；而三型值点圆弧插值法和三型值点三次多项式插值法计算得到的最大曲率值更小，均为 0.103，与极限曲率值差距较大；折角比较法计算得到的最大折角值2.947°约为极限折角值 8.008o的 0.37倍，差距也较大。5种方法计算得到的最大曲率和最大折角发生在9.5～10.0 m深度位置，与9月8日现场监测过程中测斜探头在 10.0～10.5 m 深度位置受阻的情况基本吻合。显然，五型值点单点约束拟合双圆弧法无论是曲率还是深度的计算结果都最符合实际。因此，本文推荐采用该方法作为测斜管失效判别方法。

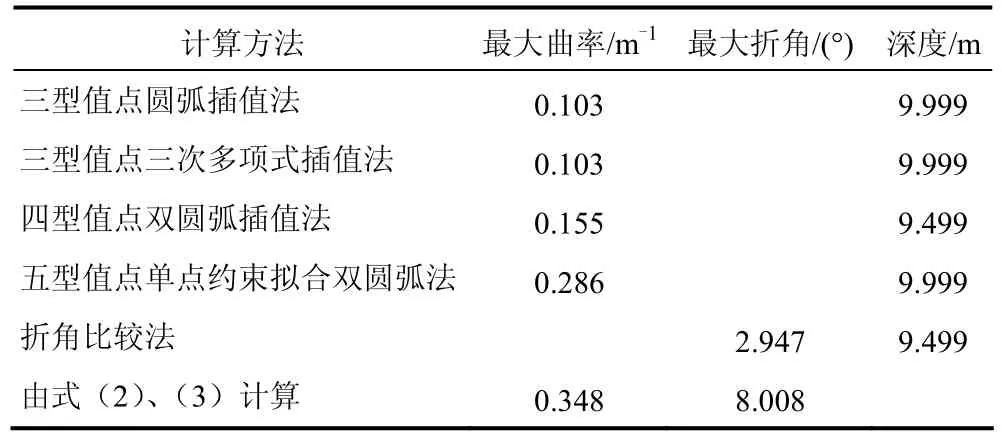
表2 计算得到的最大曲率和折角Table2 Calculated maximum curvature and deflection angle

5 结 语

针对测斜管失效问题，本文提出5种确定测斜管局部变形曲线的曲率或折角的方法，分别是三型值点圆弧插值法、三型值点三次多项式插值法、四型值点双圆弧插值法、五型值点单点约束拟合双圆弧法和折角比较法。采用这些方法，针对监测数据所确定的最大曲率或最大折角与测斜管失效时的极限曲率或极限折角进行对比，以评判测斜管失效的可能性。

通过对某地铁车站基坑工程现场施工监测过程中1根测斜管的失效实例分析结果表明，五型值点单点约束拟合双圆弧法能够较好地预测测斜管的失效。但该方法的适用性还有待于更多的工程实践检验。

[1]陈绪禄. 活动应变式测斜仪[J]. 岩土工程学报,1983,5(4):92－102.CHEN Xu-lu. Movable inclinometer in type of strain gauge[J]. Chinese Journal of Geotechnical Engineering,1983,5(4): 92－102.

[2]LEI G H,AI Y B,SHI J Y. The interpretation of pendulumtype inclinometer readings[J]. Canadian Geotechnical Journal,2006,43(2): 210－216.

[3]MIKKELSEN P E. Advances in inclinometer data analysis[C]//Proceedings of the 6th International Symposium on Field Measurements in Geomechanics,FMGM 2003.Olso,Norway: BALKEMA A A,2003: 555－567.

[4]SIMEONI L,MONGIOVI L. Inclinometer monitoring of the Castelrotto landslide in Italy[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2007,133(6):653－666.

[5]DESCHAMPS R,HYNES C,WIGH R. Extending the period of data retrieval for vertical inclinometers[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1998,124(5): 454－456.

[6]李积胜. 测斜仪与测斜导管参数关系计算方法[J]. 露天采煤技术,1997,(1): 37－39,26.LI Ji-sheng. Calculation method of the relationship between inclinometer probe and casing parameters[J]. Opencast Coal Mining Technology,1997,(1): 37－39,26.

[7]OOI P S K,RAMSEY T L. Curvature and bending moments from inclinometer data[J]. International Journal of Geomechanics,ASCE,2003,3(1): 64－74.

[8]孙家昶. 样条函数与计算几何[M]. 北京: 科学出版社,1982.

[9]孙家昶. 局部坐标下的样条函数与圆弧样条曲线[J]. 数学学报,1977,20(1): 28－40.SUN Jia-chang. Spline functions and arc spline curves in a local coordinate[J]. Acta Mathematica Sinica,1977,20(1):28－40.

[10]王英惠,吴维勇. 基于分段与识别技术的平面轮廓的精确重构[J]. 工程图学学报,2007,27(5): 43－48.WANG Ying-hui,WU Wei-yong. Accurate reconstruction for planar contour based on segmentation and recognition techniques[J]. Journal of Engineering Graphics,2007,27(5): 43－48.