基于A*定长搜索算法的多无人机协同航迹规划

肖自兵, 袁冬莉, 屈耀红

(西北工业大学 自动化学院, 陕西 西安 710129)

基于A*定长搜索算法的多无人机协同航迹规划

肖自兵, 袁冬莉, 屈耀红

(西北工业大学 自动化学院, 陕西 西安 710129)

基于多无人机同时作业情况下的航迹规划问题,提出了一种A*定长航迹搜索算法。该算法通过选择代价值最接近给定值的节点作为最佳节点,得到定长规划航迹,接着进一步通过限定最佳节点的选择范围,改善了航迹的可飞性。仿真结果表明,利用该算法规划的定长航迹长度误差可以控制在1.4%以内,协同航迹长度误差可以控制在0.8%以内,能够满足多无人机同时到达的一般要求。

无人机; A*算法; 协同航迹规划; 航迹代价

引言

多无人机协同作业在军事领域有着重要的意义,近年来成为国内外研究的热点。多无人机的协同航迹规划是一个复杂的问题,包含了无人机物理会合约束、作业环境约束和其他操作要求约束[1]。

选择算法是协同航迹规划的重要一环,适宜的航迹搜索算法在没有人工干预的条件下,能够使无人机有效地规避障碍[2]。常用的航迹搜索算法有Dijkstra算法、Bellman Ford算法、Floyd-Warshall算法和A*算法等[3]。A*算法通过构造启发函数提高了搜索效率,成为静态路网中求解最短路径(或航迹)的有效方法[4]。然而A*算法多应用于单机航迹规划,不能用于多机协同航迹规划。文献[5-7]对A*算法进行了改进,这些改进措施虽然优化了规划结果或提高了搜索效率,却仍然局限于单机航迹规划应用,不能实现多机协同航迹规划。

本文提出了一种A*定长航迹搜索算法。用该算法可以实现定长航迹规划,进而实现多无人机的协同航迹规划。

1 协同航迹规划问题

1.1 问题描述

假设N架无人机在时刻t0分别处于不同位置S1,S2,…,SN,要求在同一时刻t1到达N个不同目标点D1,D2,…,DN,实施打击且代价最小。飞经区域存在雷达和导弹阵地威胁,设各无人机匀速飞行且航速相同。

1.2 协同航迹规划原理

多无人机协同航迹规划总体结构[8]如图1所示。

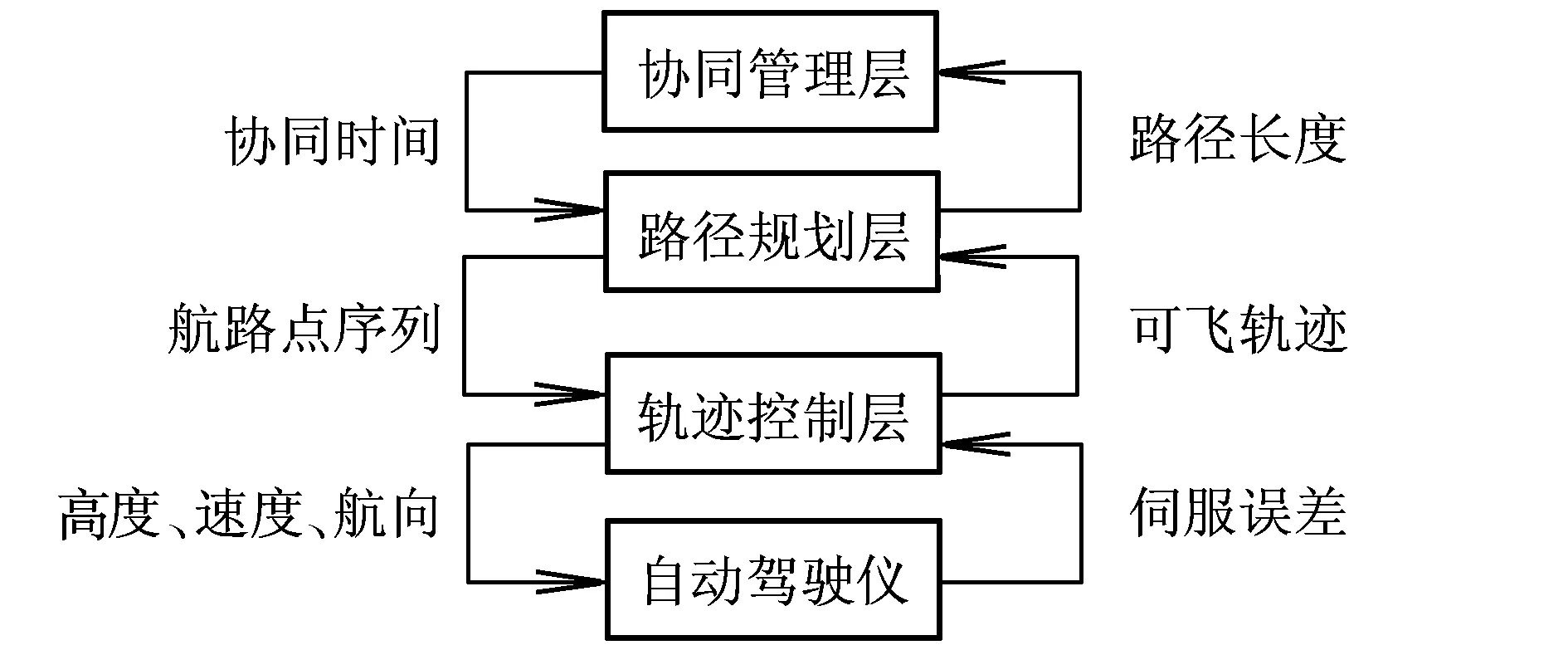
图1 多无人机协同航迹规划总体结构图

整个工作过程大致是:协同管理层根据战场环境、无人机速度的变化范围以及路径规划层传来的路径长度,确定出编队的协同时间t,并把t和各无人机的相应路径编号送到路径规划器;路径规划器把协同管理层确定的t和相应的路径航路点序列送到轨迹控制层;轨迹控制层根据航路点序列确定可飞轨迹以及相应的控制向量,并把求得的可飞航迹的高度、速度和航向送到无人机自动驾驶伺服系统去执行,操纵无人机按规划出来的航迹飞行。

一类协同航迹规划问题为多机同时到达问题。为了使各无人机能够同时到达目标,通常采用两种方式:一种是通过调节无人机的飞行速度使航程较大的无人机采取较大的速度,而航程较小的无人机采取较小的速度;另一种是对航路进行修正,通过增加较短航路的长度使每架无人机的航程大致相等。

1.3 航迹代价

当飞行区域存在地面雷达或地空导弹威胁时,一种代价计算方法[9]为:

J=kJt+(1-k)Jf

(1)

式中,J为航迹总代价;k为威胁权重系数,由规划者根据实际情况给出;Jt为雷达或导弹威胁代价;Jf为燃油代价。

为使问题简化,本文只考虑航程代价(与燃油代价成正比),而使无人机完全绕开地面雷达和地空导弹的威胁,即威胁代价为0(对应上式中k=0)。

2 A*算法原理

A*算法是一种经典的启发式搜索算法,其代价函数为:

f(n)=g(n)+h(n)

(2)

式中,f(n)为节点n从初始点到目标点的估计代价,称为代价函数;g(n)为在状态空间中从初始节点到n节点的实际代价(即已走路径代价);h(n)为从n到目标节点最佳路径的估计代价,称为启发函数。

3 航迹规划

3.1 A*定长搜索算法与定长航迹规划

A*算法的搜索策略是:选取Open表中f值(代价)最小的节点作为最佳节点加以扩展,得到代价最小的航迹。如果重新定义最佳节点,应能规划出不同的航迹。

修改A*算法如下:选取Open表中f值(航程)最接近于给定长度f0的节点作为最佳节点加以扩展。如此当能规划出长度为f0的定长航迹,从而为多无人机协同航迹规划奠定了基础。改进后的A*算法由于采用了定长搜索策略,称其为A*定长搜索算法,将分别在下面介绍的两种情形下应用。

情形1:设无人机飞经区域100 km×100 km范围内共40个威胁点(雷达阵地和导弹阵地),且设任意两个威胁点的间距大于无人机安全距离的两倍,无人机沿这些威胁点生成的Voronoi图边线飞行。

情形2:在400 km×400 km的区域内分布着6个威胁区域(雷达阵地和导弹阵地),地图比例尺取为1∶10。地图栅格划分及节点扩展方式如下:用间距为10 km的水平线和竖直线将该大小为400 km×400 km的正方形栅格化,使得每个网格均为10 km×10 km的正方形,所有网格的顶点均作为可扩展的节点。除边界上的点外,每个节点都按8个方向进行扩展以到达相邻的8个节点,节点扩展方式如图2所示。

图2 节点扩展示意图

设情形1下无人机的起始位置S的坐标为(10,10) km,起始时刻t0为8∶00,所要到达的目标点D的坐标为(40,85) km,要求的到达时刻t1为8∶15,且设无人机的航速为v=200 m/s。

设情形2下无人机的起始位置S的坐标为(10, 30) km,起始时刻t0为8∶00,所要到达的目标点D的坐标为(360,300) km,要求的到达时刻t1为8∶50,且设无人机的航速为v=200 m/s。

情形1中因为采用的是Voronoi图,最佳节点只能是Voronoi节点,而无人机的起始点和目标点不一定与Voronoi节点重合。为此,直线连接起点S(xS,yS)和最近的Voronoi节点A(xA,yA)并计算长度:

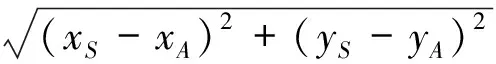
(3)

直线连接终点D(xD,yD)和最近的Voronoi节点B(xB,yB)并计算长度:

(4)

则中间应规划航迹长度为dc=f0-c1-c2,接下来只要进行起始点为A、目标点为B、给定长为dc的定长航迹规划就可以了。

情形2中为使航迹在长度上更精确,采用图2所示的节点扩展方式,这就决定了航迹上可能出现的角度分别为45°,90°,135°,180°,而45°和90°的角将影响航迹的可飞性。以往处理的办法是对所生成的航迹进行平滑处理,这就将航迹规划工作人为地分为了两个部分,且平滑工作较为繁杂。这里通过对算法进行进一步的改进来改善航迹的可飞性。

航迹上出现直角甚至锐角的原因是最佳节点的选择范围过大,为此,对算法进行进一步改进:从最新添加进Open表的节点(也即上一循环中既不属于Open表也不属于Closed表的扩展节点)中选择最佳节点,这从根本上杜绝了锐角的产生,且能降低直角发生率,具体分析如下。

图3为航迹角度控制示意图。图中,符号“○”表示节点。

图3 航迹角度控制示意图

搜索过程如下:

(1)选择A点作为最佳节点,扩展A点,产生后继节点D,B,E,将D,B,E点加入Open表。

(2)从最新添加进Open表的节点D,B,E中选择最佳节点。假设为B,扩展B点,产生后继节点F,C,G,H,I,E,A,D,将F,C,G,H,I添加进Open表(E,A,D已在Open表,不需再添加)。

(3)从最新添加进Open表的节点F,C,G,H,I中选择最佳节点。如果选F,则∠ABF=90°;如果选C,则∠ABC=135°;如果选G,则∠ABG=180°;如果选H,则∠ABH=135°;如果选I,则∠ABI=90°。由于避免了选择E和D作为最佳节点,当前航迹不会出现锐角(45°)。假设最佳节点选为C,扩展C点,产生后继节点J,K,L,G,H,B,D,F,将J,K,L添加进Open表(G,H,B,D,F已在Open表,不需再添加)。

(4)从最新添加进Open表的节点J,K,L中选择最佳节点。如果选J,则∠BCJ=135°;如果选K,则∠BCK=180°;如果选L,则∠BCL=135°。由于避免了选择H和D作为最佳节点,当前航迹不会出现锐角(45°),又由于避免了选择G和F作为最佳节点,当前航迹不会出现直角。

上述分析表明:针对算法的改进措施可以有效地改善航迹的可飞性。但这样会导致一个问题:由于最佳节点的选取范围缩小了,导致不一定能搜索到目标节点,可能会与之“擦肩而过”,以致造成程序“死循环”。为避免这种情况的发生,需要修改程序终止的条件,将“搜索到的最佳节点为目标节点”这一条件改为“搜索到的最佳节点与目标节点较为接近”。

情形1中不能通过这样进一步的算法改进来改善航迹可飞性,其原因是Voronoi图中每个节点只有3个扩展方向,下一个最佳节点只能从这3个点中选取,如果再缩小选择范围,就可能导致找不到最佳节点而使搜索无法继续。

3.2 多机协同航迹规划

在用改进的A*算法实现定长航迹规划后,可进一步实现多无人机协同航迹规划。以3架无人机为例,其策略为:根据起始点、目标点以及途中要规避的威胁,3架无人机先各自进行最短航迹规划,然后从中选取长度最大的一条作为参照,以其长度作为给定值,对其他两架无人机进行定长航迹规划。这样就实现了3机同时出发、同时到达且用时最短的协同航迹规划。

设在上述情形1下,第1架无人机的起始点S1坐标为(10, 10) km,目标点D1坐标为(70, 70) km;第2架无人机的起始点S2坐标为(5, 40) km,目标点D2坐标为(70, 95) km;第3架无人机的起始点S3坐标为(30, 10) km,目标点D3坐标为(90, 70) km。

设在上述情形2下,第1架无人机的起始点S1坐标为(10, 10) km,目标点D1坐标为(270, 270) km;第2架无人机的起始点S2坐标为(10, 110) km,目标点D2坐标为(290, 360) km;第3架无人机的起始点S3坐标为(70, 10) km,目标点D3坐标为(340, 280) km。

4 仿真结果及分析

在MATLAB环境下,进行上述单机定长航迹规划和3机协同航迹规划数字仿真。

启发函数取为当前节点到目标节点直线距离的1.4倍。1.4为启发系数,决定了启发函数h(n)的大小。

计算可得情形1下无人机应飞航迹的给定长度为f0=v(t1-t0)=180 km,情形2下无人机应飞航迹的给定长度为f0=v(t1-t0)=600 km。

图4为第一次改进的A*算法在情形1下的定长航迹规划结果,航迹长度为179.309 6 km,与理论应飞航程180 km非常接近,相对误差为0.383 6%。

图4 情形1下定长规划结果

图5为第一次改进的A*算法在情形2下的定长航迹规划结果,航迹长度为592.132 km,与理论应飞航程600 km较为接近,相对误差为1.311 3%。但同时看到图中航迹出现了较多的直角,有些地方甚至出现了锐角,这使得航迹的可飞性受到很大影响。

图5 情形2下定长规划结果

图6为进一步改进的A*算法在情形2下的定长航迹规划结果,航迹长度为599.411 km,与理论应飞航程600 km非常接近,相对误差为0.098 2%。相对于图5而言,尽管图6中航迹仍然包含少许直角,其可飞性还是得到了很大改善,基本满足飞行要求。

图6 改善可飞性的定长航迹

图7为在情形1下3机协同航迹规划的仿真结果,3条航迹(从上到下)的长度分别为97.506 4,98.235 9,97.591 3 km,较为接近(相对于中间的参考航迹,上面航迹的误差为0.742 6%,下面航迹的误差为0.656 2%),满足3机同时出发、同时到达的协同航迹规划要求。

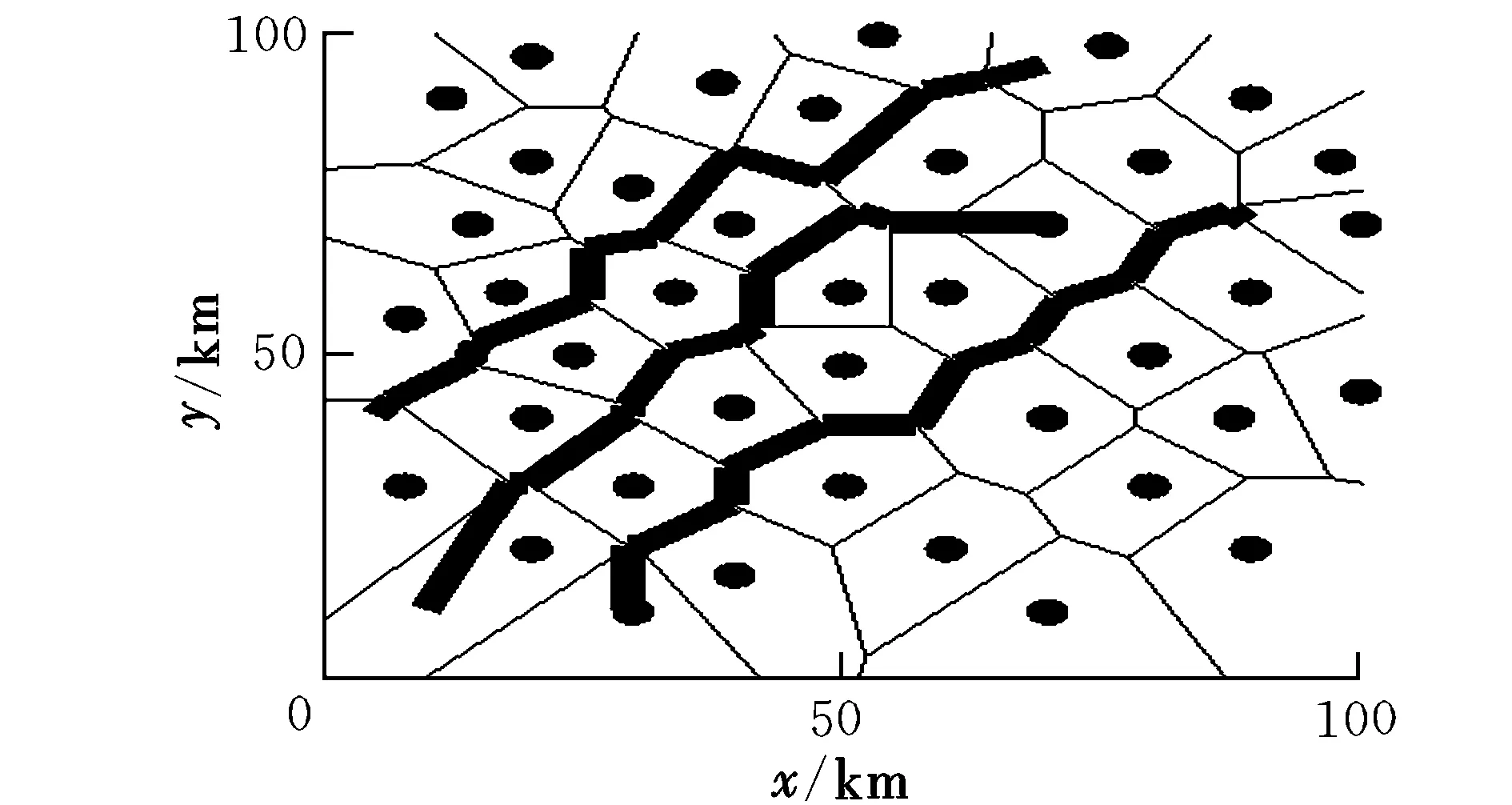
图7 情形1下的协同航迹

图8为在情形2下3机协同航迹规划的结果,3条航迹(从上到下)的长度分别为403.553,405.269,405.269 km,较为接近(相对于下面的参考航迹,上面航迹的误差为0.423 4%,中间航迹的误差为0),满足3机同时出发、同时到达的协同航迹规划要求。

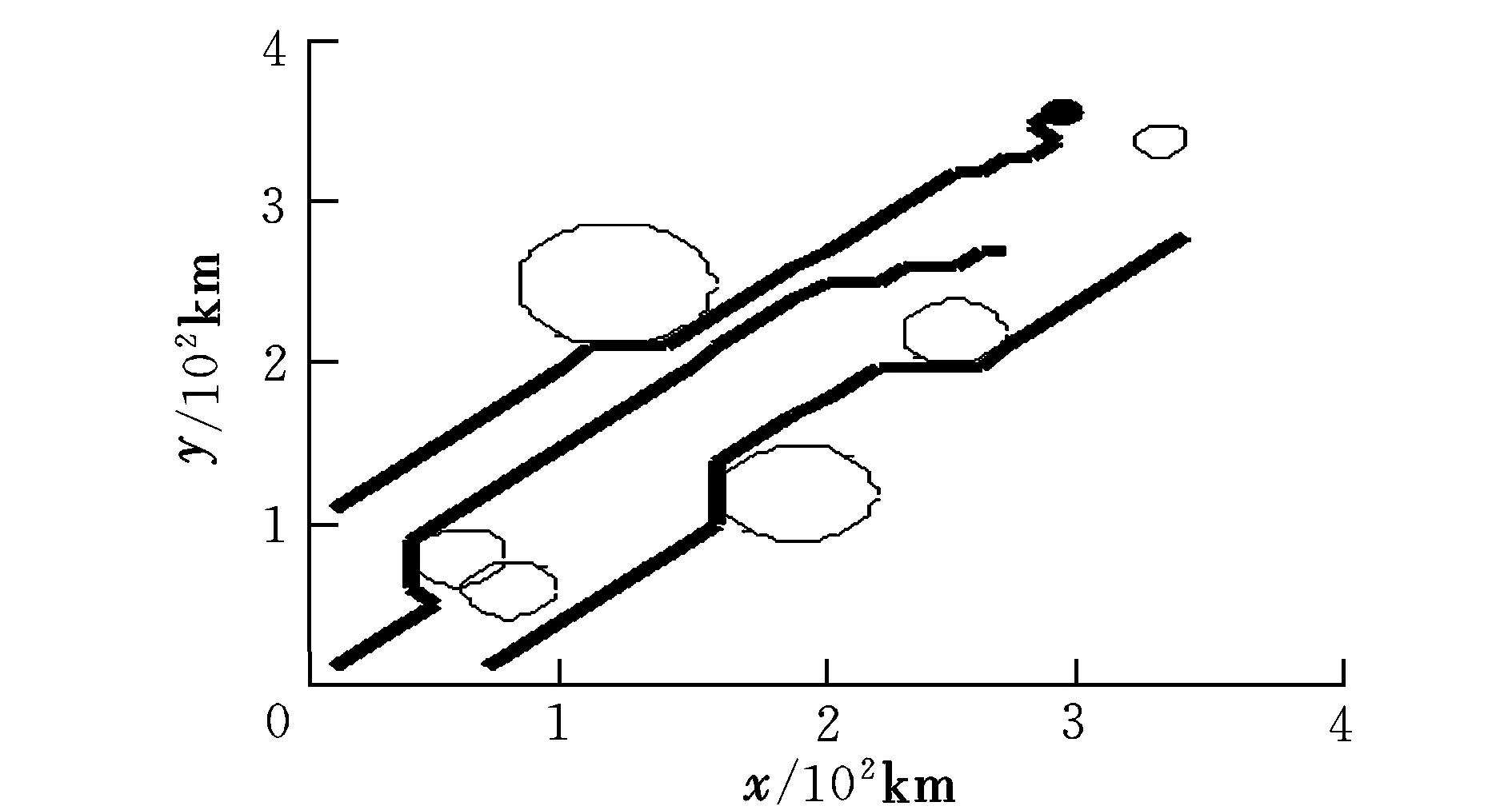
图8 情形2下的协同航迹

5 结束语

本文通过对A*算法进行改进,提出了一种A*定长航迹搜索算法,用该算法规划出了定长航迹,并以此为基础实现了多机协同航迹规划,仿真结果证明了算法的有效性。本文研究的多机协同航迹规划问题为静态路网中的各无人机同时到达问题,对于其他协同航迹规划问题,如动态规划情形,还有待今后进一步探讨。所做工作对今后无人机航迹规划有一定的借鉴意义。

[1] Shanmugavel M,Tsourdos A,White B,et al.Co-operative path planning of multiple UAVs using Dubins paths with clothoid arcs[J].Control Engineering Practice,2010,18(9):1084-1092.

[2] Oliver M,Natalie F,Christian A,et al.Adaptive path planning for VTOL-UAVs[J].IEEE Aerospace and Electronic Systems Magazine,2009,24(7):36-41.

[3] Sathyaraj B M,Jain L C,Finn A,et al.Multiple UAVs path planning algorithms:a comparative study[J].Fuzzy Optimization and Decision Making,2008,7(3):257-267.

[4] Seo W J,Ok S H,Ahn J H,et al.An efficient hardware architecture of the A-star algorithm for the shortest path search engine[C]//2009 Fifth International Joint Conference on INC,IMS and IDC.Piscataway:IEEE Computer Society,2009:1499-1502.

[5] Li Ji,Sun Xiuxia.Route planning’s method for unmanned aerial vehicles based on improved A-star algorithm [J].Binggong Xuebao,2008,29(7):788-792.

[6] 孟中杰,黄攀峰,闫杰.基于改进稀疏A*算法的高超声速飞行器航迹规划技术[J].西北工业大学学报,2010,28(2):182-186.

[7] Dai Zhiquan,Guan Yong,Guan Ran.Dynamic adjustment A*rounting algorithm[C]//CICC-ITOE 2010 International Conference on Innovative Computing and Communication and 2010 Asia-Pacific Conference on Information Technology and Ocean Engineering. Piscataway:IEEE Computer Society,2010:316-318.

[8] 高晓光,符小卫,宋绍梅. 多UCAV航迹规划研究[J].系统工程理论与实践,2004,24(5):140-143.

[9] Meng Bobo,Gao Xiaoguang,Wang Yunhui.Multi-mission path re-planning for multiple unmanned aerial vehicles based on unexpected events[C]//2009 International Conference on Intelligent Human-Machine Systems and Cybernetics.Piscataway:IEEE Computer Society,2009:423-426.

Multi-UAVscooperativepathplanningbasedonA*fixedlengthsearchalgorithm

XIAO Zi-bing, YUAN Dong-li, QU Yao-hong

(College of Automation, NWPU, Xi’an 710129, China)

An improved A*algorithm for fixed length path searching was proposed based on the path planning problems of multiple unmanned aerial vehicles(UAVs) operating simultaneously. A path with fixed length was obtained by choosing nodes with costs closest to given value as best nodes in the algorithm. Then, the path was smoothed by limiting the range of the best nodes choosing from in the algorithm. Simulation results show that length error of the fixed length path obtained from the algorithm can be controlled within 1.4%, and length error of collaborative paths is less than 0.8%. It basically meets the requirements of multi-UAVs arriving at the same time.

unmanned aerial vehicle(UAV); A*algorithm; cooperative path planning; path costs

2011-04-18;

2011-09-04

国家自然科学基金资助(60974146)

肖自兵(1984-)，男，四川简阳人，硕士，主要研究方向为现代控制理论及应用;

袁冬莉(1966-)，女，陕西乾县人，副教授，博士，研究方向为先进控制理论及应用、导航制导与控制、计算机控制与智能控制、飞行控制与仿真等。

V279; V249.122

A

1002-0853(2012)01-0092-05

(编辑：姚妙慧)