几类整函数中函数的唯一性
2012-11-03王玉华
王玉华
(临沧师范高等专科学校数理系,云南临沧 677000)
几类整函数中函数的唯一性
王玉华
(临沧师范高等专科学校数理系,云南临沧 677000)
利用值分布理论中的展布关系对滋长级小于1的整函数的唯一性进行了研究,得到了一些结果。
整函数;值分布论;展布关系;分担值
1 引言和主要结论
定义1[1](分担值的定义)设(fz)与g(z)均为开平面上的非常数亚纯函数,a为任意确定的复数(可为∞)。如果方程(fz)=a与g(z)=a在C上有相同的根,则称a为(fz)与g(z)的分担值。若计较根的重数,则称a为(fz)与g(z)的CM分担值;若不计较根的重数,则称a为(fz)与g(z)的IM分担值。
定义2[2]设函数(fz)是开平面C上的非常数亚纯函数,下级μf<+∞,一个正数序列 {rj}∞j=1称为(fz)的μf级polya峰序列(简称为polya峰),若相应地有三个正数列{r′j}∞j=1,{r″j}∞j=1,{εj}∞j=1适合条件
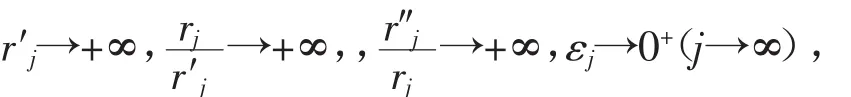
并且当r′j≤t≤r″(jj充分大)时有
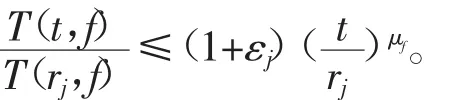
定义3[2]设函数(fz)于开平面C上的不恒为零且下级有穷的亚纯函数,{rj}∞j=1是(fz)的μf级polya峰。又设Λ(r)为一个定义在[0,+∞)上的正值函数,它满足:

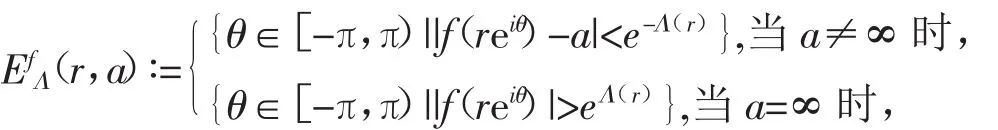
以及

以及
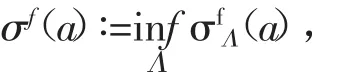
这里的下确界是对定义在R+上的所有满足(*)的正值函数Λ(r)取的。σ(fa)称为函数(fz)关于a的一个展布。
本文主要对滋长级小于1的整函数的唯一性进行了研究。所谓亚纯函数唯一性理论是探究唯一确定一个亚纯函数的非显然的充分条件。在亚纯函数唯一性理论中,涉及IM分担值的整函数的唯一性问题的研究成果非常丰富,在这方面,R.Nevanlinna所创立的值分布论也就自然的成为主要的研究工具,他本人也做了开创性的工作,在1929年证明了下述定理。
定理A[1](Nevanlinna五值定理)设(fz)和g(z)为两个非常数亚纯函数,a(jj=1,2,3,4,5)为五个判别的复数。如果a(jj=1,2,3,4,5)为(fz)和g(z)的IM分担值,则(fz)≡g(z)。
例1 整函数(fz)=ez与g(z)=e-z以0,-1,1及∞为IM分担值,但(fz)不恒等于g(z)。
上述例子表明对于一般的非常数亚纯函数,5个IM分担值的条件不能减弱,但是对于有穷非正整数级的亚纯函数来说,条件是否可以再减弱呢?对于受一定的滋长性限制的两个非常数亚纯函数是否可以由它们分担4个,3个甚至2个IM分担值而确保它们恒等呢?这就启发我们讨论有穷非正整数级的整函数的唯一性问题,本文主要对滋长级小于1的整函数的唯一性进行了研究。
对于级小于1的非常数整函数的情形,李玉华于2000年得到了以下结论。
定理B[3]若两个级小于1的非常数整函数(fz)与g(z)有2个有穷的IM分担值a和b,且存在正常数G和r,使
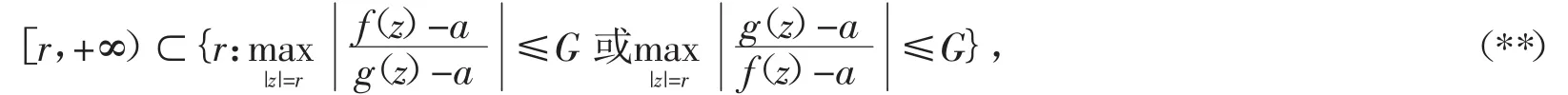
则一定有(fz)≡g(z)。
定理B中的条件(**)能否去掉或用更简洁的条件来取代呢?对此,蔡翠于2005年得到了以下结论。
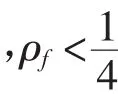
何萍于2008年,利用级小于1/2的非常数整函数的独特性质将定理C作了以下改进。

在本文中,主要利用展布关系,证明了以下几个结果。
定理1 设(fz)与g(z)是级小于1的非常数整函数,它们以判别有穷复数a,b为IM分担值。如果存在正数d,ε0,r0,使得对∀r≥r0有
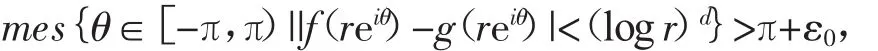
则一定有(fz)≡g(z)。
定理2 设(fz)与g(z)是滋长级小于1的非常数整函数,它们以判别的有穷复数a,b为IM分担值。如果存在正数d,ε0及r0,使得对于∀r≥r0有
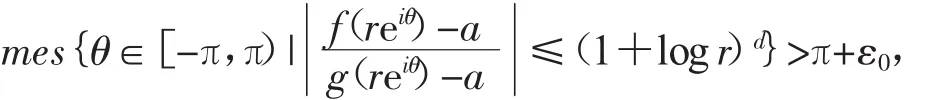
则一定有(fz)≡g(z)。
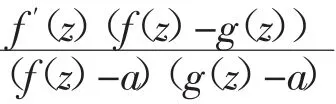
定理4 设(fz)为非常数整函数,n为正整数,p(z)为n次多项式。如果p((fz))与f′(nz)具有两个有穷的IM分担值a和b,则(fz)的级ρf≥1。
2 几个引理


引理2[2](展布关系)设函数(fz)为开平面C中的非常数亚纯函数,其下级μf<+∞。若复数a是(fz)的一个亏值,则
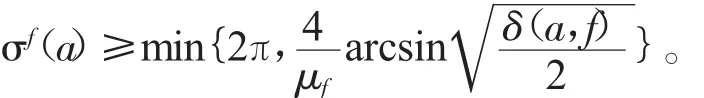
引理3[4]设(fz)与g(z)是级小于1的非常数整函数。如果
(i)0和1为(fz)与g(z)的IM分担值;
则一定有(fz)≡g(z)。
引理4[2]设(fz)为非常数整函数。如果

则(fz)一定为多项式函数。
引理5[6]设(fz)为非常数整函数,且ρf<1,则
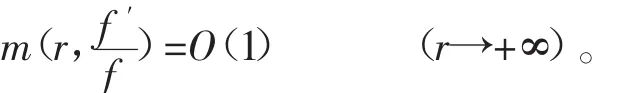
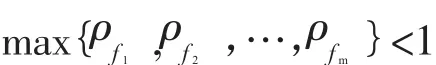
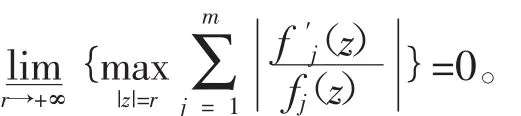
引理7[2]设(fz)为开平面上的超越亚纯函数,则使Θ(a,f)>0的值a至多是可数的,并且
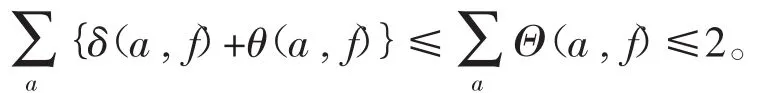
3 定理1的证明
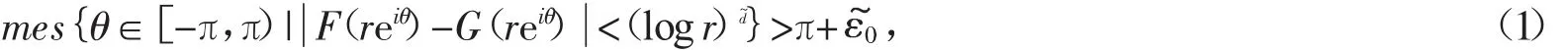
继令

则φ(z)为级小于1的整函数。
下面分两种情况进行讨论。
情形1 φ(z)为多项式。
这时,由引理3知F(z)≡G(z),从而有(fz)≡g(z),此即为欲证之结论。
情形2 φ(z)为超越整函数。
这时,注意到δ(∞,φ)=1,以及0≤μφ<1,从而有
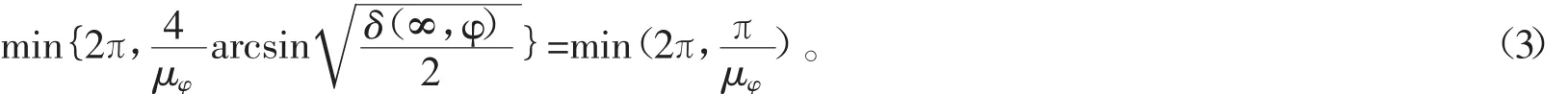
所以∃δ0>0,使

由此并结合引理2知存在φ(z)的μφ级polya峰 {rj}∞j=1使得
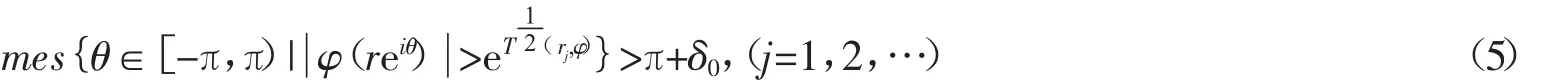
兹对∀充分大的j,令
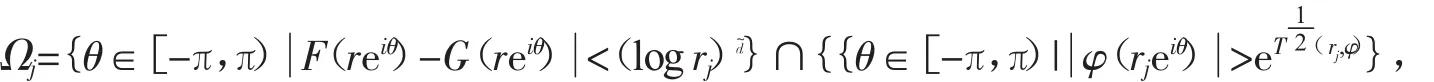
则由(1)和(5)知对充分大的j有,

注意到,对充分大的j有

由于φ(z)为整函数,故由(6)和(7)知对充分大的j有,

由(8)和引理5得

因rj→+∞(j→∞),从而由(9)和引理4知φ(z)一定为多项式,矛盾。
定理1证毕。
4 定理2的证明
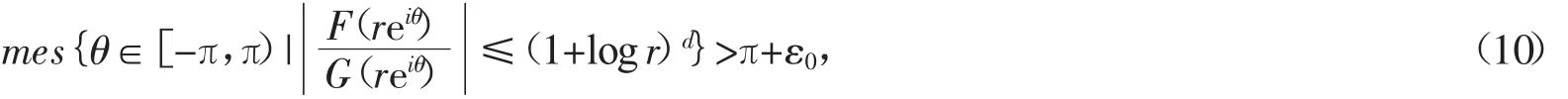
继令

则φ(z)为整函数,且0≤μφ≤ρφ<1。
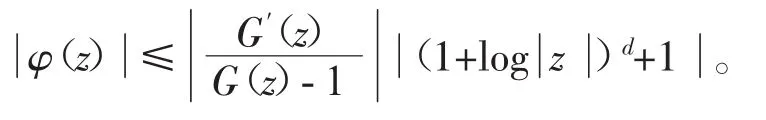
类似于定理1证明过程中的讨论,可导出所期望的结论。
定理2证毕。
5 定理3的证明
不失一般性,不妨设a=0,b=1,令

则φ(z)和ψ(z)都为级小于1的整函数,且

如果φ(z)或ψ(z)是多项式函数,则由引理3知(fz)=g(z)。
如果ψ(z)与φ(z)为超越整函数,对φ(z)应用引理1知存在正数列{r}j∞j=1使,
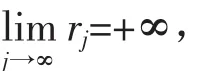
且充分大的j,当rj≤t≤min{j,log r}jrj时有
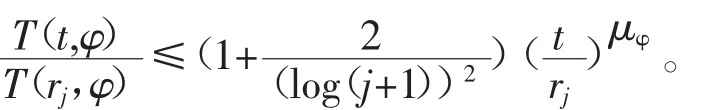
如果μψ=0,则定理结论成立。
如果1>μψ>0,由于ψ(z)是正规增长的有穷级超越整函数,所以{r}j∞j=1亦为ψ(z)的μψ级polya峰,令
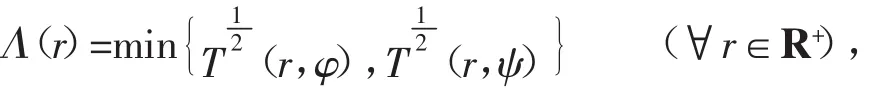
则由引理2知,∃δ0>0使对充分大的j有,
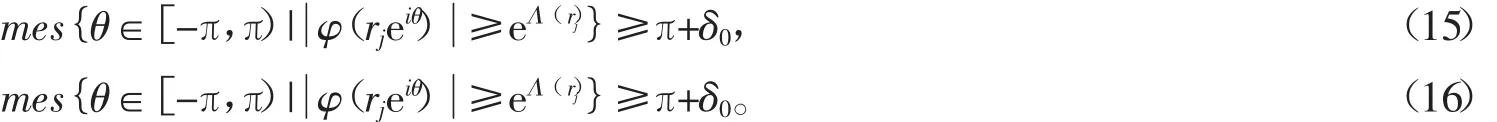
对于充分大的j,令
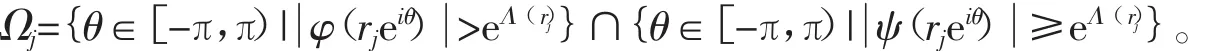
当j充分大时,

对于充分大的j,继令

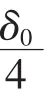

又因为对充分大的n有

据(18),(19)和引理5得
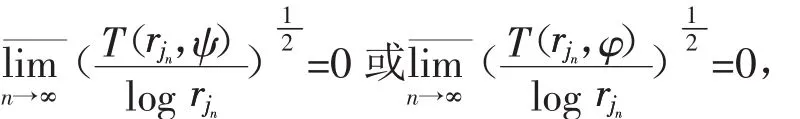
由此和引理4知ψ(z)或φ(z)是多项式函数,矛盾。
定理3证毕。
6 定理4的证明
假设ρf<1,令

则φ(z)为级小于1的整函数,ρf=ρf′=ρf″<1,由(20)和引理6知

从而有φ(z)=0,即

如果n=1,则∃A,B∈C,且A≠0,使A(fz)+B=f′(z),从而存在非零常数c,使A(fz)+B=ceAz,由此知ρf= 1,矛盾。
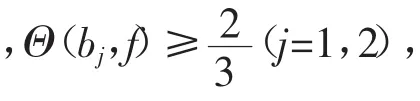
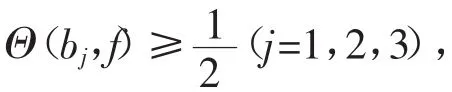

由此可得Θ(b1,f)+Θ(b2,f)>1,矛盾。
定理4证毕。
〔1〕仪洪勋,杨重骏.亚纯函数唯一性理论〔M〕.北京:科学出版社,1995.
〔2〕杨乐.值分布论及其新研究〔M〕.北京:科学出版社,1989.
〔3〕LiYuhua.Uniqueness theorems for meromorphic functions of order less than one〔J〕.Northeastern Mathematical Journal,2000,16(4):411-416.
〔4〕蔡翠.一类整函数的唯一性〔D〕.昆明:云南师范大学,2005.
〔5〕何萍.具有特殊增长级的整函数的唯一性〔D〕.昆明:云南师范大学,2008.
〔6〕顾永兴,庞学诚,方明亮.正规族理论及其应用〔M〕.北京:科学出版社,2007.
Uniqueness Theorems for Some Special Entire Functions
WANG Yuhua
(Department of Mathematics and Physics,Lincang Teachers College,Lincang,Yunnan 677000,China)
In this paper,we study the uniqueness of non-constant entire functions whose orders are less than 1 on the basis of the value distribution theory of meromorphic function and then get some findings in this aspect.
entire function;value distribution theory;spread relation;sharing value
O174.52[文献标志码]A[文章编号]1672-2345(2012)04-0005-06
2011-11-14
王玉华,讲师,主要从事复分析研究.
(责任编辑 袁 霞)
