谈数学图形在法理学教学中的应用
2012-11-02马忠泉
马忠泉
(湖北警官学院 法律系,湖北 武汉430034)
谈数学图形在法理学教学中的应用
马忠泉
(湖北警官学院 法律系,湖北 武汉430034)
形象是教学的灵魂,法理学教学要通过形象化的手段讲解抽象的理论知识。数学图形语言作为一种形象化的语言在法理学教学中有着独特的作用。
教学;法理学;形象化;数学图形
如果说创新是科研的灵魂,那么形象就是教学的灵魂。
大学教学要培养学生抽象思维的能力,但在这个过程中形象化的教学依然是不可缺少的。形象化教学,即把抽象的、复杂的理论形象地、简单地呈现给学生,依然是大学教师的主要责任和能力要求。这是教师区别于专门从事研究的工作者的主要方面,更是一个教育专家必不可少的能力与意识。
法学理论教学的形象化来源于形象的语言、生动的案例等等。数学图形也是一种形象的语言,因此,利用数学图形这种形象化的语言进行抽象的法理学教学就是自然的、可行的。本文以三个法理学上的知识点的数学图形化教学为例,来看数学方法在法理学教学中的应用。
一、法律起源和发展问题的数学图形化教学
在一般的法理学教科书中,法律的起源和发展问题是作为一编或一章的内容进行介绍的。以张文显主编的教材①张文显主编:《法理学》,高等教育出版社,北京大学出版社,2007年2月第三版,第三编。为例,本部分的内容体现为一编,共两章:第十四章,法的历史,内容分两节,第一节是法的起源,第二节是法的历史类型;第十五章,法律演进与法律发展,内容分五节,第一节是法律的演进与发展的历史规律,第二节是法律继承,第三节是法律移植,第四节是法制改革,第五节是当代中国的法律发展。分析教材的结构,其内在的思路是从理论(法律起源和发展的一般规律)到实践(实践中法律发展的形式表现为继承、移植和改革)、从一般(世界范围内的法律起源和发展)到具体(我国的法律发展)。但是这样的思路是适合于一切知识体系的安排的,没有体现对具体的法律起源和发展这一法理问题的内在逻辑的抽象,并且在内容的安排上存在一个重要的缺陷,就是本质上依然属于法律的演进和发展问题的法的历史类型的更替这一知识点并没有安排在法律的演进和发展这一章中,人为地割断了知识的内在链条。笔者认为,本章的核心教学目标是让学生掌握法律演进和发展的一般规律和法律演进和发展的主要途径(或形式)。理解主导法律发展的不同途径(形式)决定了法律发展的特征(主要体现为速度的快慢)。基于此,笔者在教学中把这一编的内容形象地表现在一条总体上呈反S曲线的一条波浪线上。如图一所示。
这条曲线总体上是呈反S形的,它揭示出法律发展和一般的社会事物发展一样,在其产生之初,发展的速度很慢。当经过一定时间的条件积累之后,法律的发展速度会加快。但这样快的发展速度不会一直持续下去,法律的发展会在发展成熟后趋于平衡。
总体上呈反S的曲线内部的波浪表示法律发展在具体的时间段内又呈现出次一级的反S型曲线的发展模式。每一个次一级的反S曲线分别代表着同一历史类型的法的发展过程。即图中 OO1、O1O2、O2O3、O3O4四个区间内的曲线分别代表着奴隶社会法的发展、封建社会法的发展、资本主义社会法的发展和社会主义社会法的发展。对应的四个线段的分界点1、2、3处(事实上是一个很短的时间段,即BA1、B1A2、B2A3)法律的发展和演变过程表现为法律的历史类型的更替,法律发生了质变,法律发展的途径(或形式)主要是法律革命。在每一种历史类型的法的发展过程中,都有发展相对缓慢的时期和发展相对迅速的时期。其中OA、O1A1、O2A2、O3A3所表示的四个区间内的曲线,法律发展的过程表现为法律的演变。法律发展的速度很缓慢,法律发展的途径(或形式)主要是法律继承。在 AB、A1B1、A2B2、A3B3所表示的四个区间内的曲线,法律发展的过程表现为法律的突变。法律发展的速度突然变得很快,法律发展的途径(或形式)主要是对外的法律移植和对内的法律改革。

图一
这样的教学方法设计,就将整个一编的主要教学内容,包括法的历史类型、法律发展的规律、法律继承、法律移植、法制改革等都整合在一个曲线中,并且归纳出了各个知识点之间的内在逻辑关系。不仅使学生更容易理解,而且通过对曲线图的回忆,更能加深学生对知识点的记忆。
二、自然法以及自然法与实在法关系问题的数学图形化教学
自然法是西方三大法学流派中自然法学派的核心概念,自然法与实在法的关系问题是自然法学的核心问题。自然法学认为自然法是客观存在的,是永恒的、普遍的,一切实在法都是对自然法的模仿,实在法不能违反自然法。
进入现代以来,随着三大法学流派的相互融合,无论是分析法学还是社会学法学,都一定程度上承认存在某种“自然法”,也都重视阐述“自然法”和实在法的关系问题。如新分析法学派的代表哈特阐述了其“最低限度的自然法”的思想,“最低限度的自然法”即指任何一个社会都存在的禁止暴力杀人、盗窃、诈骗等规则。他表述为:“这些以有关人类的自然环境和目的的基本事实为目的的,普遍认可的行为原则,可以被认为是自然法的最低限度的内容,”[1]又如法国著名社会学法学家狄骥将建立在社会合作与分工基础之上的最高原则称之为“客观法”(objective law),认为它不同于实在法,其在国家出现以前就已存在,且存在于国家之外,国家的职能就在于实现“客观法”。因而“客观法”高于国家及其制定的实在法。狄骥的带有先验性质的高于实在法的“客观法”的确含有自然法的倾向。因此,有些学者称他为披着社会学外衣的自然法学家。我们也可以说狄骥的这一思想是披着科学外衣的自然法思想。他所阐述的“客观法”及“客观法”与实在法的关系实质上就是“自然法”及“自然法”与实在法的关系。
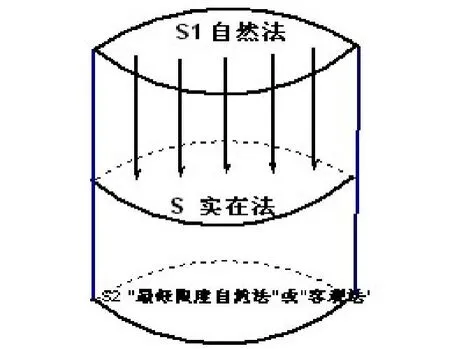
但是,对于本科生来说,什么是自然法学派思想家们所说的自然法,自然法与实在法的关系到底是怎样的,自然法学派的自然法观念和实证主义法学派(包括分析实证主义法学派和社会实证主义法学派)的自然法观念到底有何区别,这些问题是很难理解的。所以,笔者在教学中,将这些问题用一个圆柱体展示出来。如图二所示。
在图中,圆柱体的顶面S1表示自然法,圆柱体的中间截面S表示实在法,圆柱体的底面S2表示实证主义法哲学家们所阐述的“最低限度的自然法”(哈特的观点)或“客观法”(狄骥的观点)。由图可知,自然法是高于实在法的,自然法是实在法的理念、形式或模板,它是永恒的、普遍的、不变的。实在法只是自然法在世俗世界的投影而已。这就是自然法学派的法哲学家们的核心观点。而实证主义法哲学家们对于自然法的观点却恰恰相反,它们所阐述的“最低限度的自然法”或“客观法”根本不是理念世界的原则。它们恰恰是现实世界法律规范的最底层、最基础的一些规范。自然法并不高于实在法,相反它却是实在法的根基。①事实上,这种观念在新自然法学派代表富勒的程序自然法思想中也有体现。
应该说这样的形象化展示,使学生对于自然法有更深入的理解、也能更好地区别开自然法与实在法,以及自然法学派的自然法观念和实证主义法学派的“自然法”观念。
三、霍菲尔德的权利与义务分析理论的数学图形化教学
威斯利·霍菲尔德(Wesley NHohfield)是美国著名的分析法学家,他在《司法推理中的基本法律概念》(Fundamental Legal Conceptions as Applied in Judicial Reasoning)一文中提出了“法律的最低的共同标准”的法律八大基本概念,即:无权利(No-right)、权利(Right)、义务(Duty)、优先权(Privilege)、无资格(Disability)、权力(Power)、责任(liability)、豁免权(Immunity)。霍菲尔德延续了奥斯丁的“主导法律观念”的分析方法(霍费尔德称之为“法律关系”(Legal Relations)),并进一步用逻辑学中的“相对关系”和“相关关系”深入地分析了八个法律基本概念及其关系。[2]
霍菲尔德认为八个基本概念之间或者是一种相对关系,或者是一种相关关系。相对关系即指两个概念之间是对立关系,不能同时存在于同一个法律关系当中。可以形象地表述为“有你没我,有我没你”的关系。霍菲尔德认为在相对关系中,“无权利”与“权利”相对,“义务”与“优先权”相对,“无资格”与“权力”相对,“责任”与“豁免”相对。相关关系是指两个概念之间相辅相成,任何一个概念都不能单独存在,必然存在于同一个法律关系中的一种关系。可以形象地表述为“你中有我,我中有你”的关系。在相关关系中,“义务”与“权利”相关,“无权利”与“优先权”相关,“责任”与“权力”相关,“无资格”与“豁免权”相关。
图二
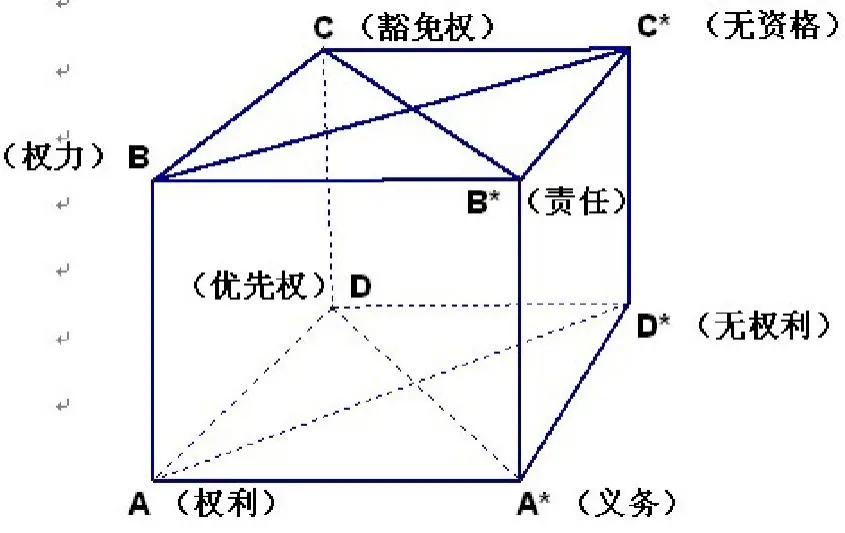
霍菲尔德这种对于权利义务的分析是精细化的,所以显得琐碎,学生在学习时不容易把握。表现为,首先是不容易记忆八个概念,因为习惯上我们只是分析权利和义务一组概念;其次是不容易记忆哪些概念是相对关系,哪些概念是相关关系。为了让学生容易理解,笔者在教学中构建出一个正方体,用正方体的八个顶点分别表示权利的四种表现形式和义务的四种表现形式,用正方体的一些的对角线表示四种相对关系,用正方体的一些边表示四种相关关系。如图三所示。
图三
在图中A点表示权利、B点表示权力、C点表示豁免权、D点表示优先权、A*点表示义务、B*点表示责任、C*点表示无资格、D*点表示无权利。那么,四条对角线AD*、A*D、BC*、B*C就分别表示出权利和无权利、义务和优先权、权力和无资格、责任和豁免权四种相对关系。四条边AA*、BB*、CC*、DD*就分别表示出权利和义务、权力和责任、豁免权和无资格、优先权和无权利四种相关关系。
经过这样的数学图形化处理后,整个内容就形象了、立体化了。联想起立方体的空间图形,学生对霍菲尔德的八个基本概念、四组相对关系概念、四组相关关系概念很容易地就记住了,也不会在相对关系和相关关系上产生混淆。总之,整个内容不仅容易被学生理解,更容易被学生记忆。
四、总结与展望
应用数学图形化语言对法理学知识进行阐释不仅能将法理学的抽象理论形象化,更利于学生理解和记忆。有时还会让我们从中发现新的问题,使理论的进一步发展成为可能。如在前文笔者构建的关于霍菲尔德理论的正方体图形中,我们会发现AB、DC、A*B*、D*C*四条边分别对应了权利-权力、优先权-豁免权、义务-责任、无权利-无资格四组概念之间的关系。这四组概念内在的关系至少可以抽象为四组概念中,每一组的后一个概念是前一个概念在量上的累加的结果。即权力是权利的量的累加、豁免权是优先权的量的累加、责任是义务的量的累加、无资格是无权利的量的累加。①就笔者的阅读范围,除了霍菲尔德,目前还没有就这几组概念的关系的法理分析。但无疑这是一个重要的法理发现,而这一发现足以说明应用数学语言重述法理问题的重大意义。可见,将法理学的理论用数学语言表达出来对于法理学的发现式学术研究是有帮助的。事实上,应用数学方法进行法理学的研究已经有了非常成功的案例。②如美国当代著名的社会学法学家唐纳德·J·布莱克于1976年出版的《The Behavior Of Law》(《法律的运作行为》)一书,成功地运用数学方法对法律的各种变化进行了定量分析和预测。该书也和梅因(HenryMaine)的《古代法》,以及埃利希(EugenEhrlich)的《法社会学的基本原理》并列成为社会学法学的经典著作。
最后笔者要说明的是,本文强调数学图形化语言在法理学教学中应用的价值,并不否认传统法理学教学的理论体系的讲授的价值,也不否认法理学教学中一直存在着形象化的教学方法,如案例教学、知识的表格化处理等等。本文的意义在于,为法理学抽象的理论教学提够一种新的方法。
[1][美]哈特.法律的概念[M].北京:中国大百科全书出版社,1996:188.
[2][美]霍菲尔德.基本法律概念[M].张书友编译.北京:中国法制出版社,2009:26-78.
G642.04
A
1673―2391(2012)09―0178―03
2012—06—17
马忠泉,湖北警官学院法律系。
【责任编校:周文慧】
