“代数式求值问题”的解题方法
2012-11-02张彦杰
张彦杰
(濮阳市职业中专,河南 濮阳 457000)
“代数式求值问题”的解题方法
张彦杰
(濮阳市职业中专,河南 濮阳 457000)
本文就“代数式求值问题”,从变形这个角度进行分类,并给出相应的解法。通过掌握数学方法解决数学问题是高效率数学教学的途径。
整体代值;因式分解;倒数;非负数的性质
代数式求值问题是数学教学中的基本内容之一,熟练掌握代数式求值问题是数学教学的基本要求,而代数式求值问题形式多样,变化丰富多彩。代数式的求值与代数式的恒等变形关系十分密切,许多代数式是先化简再求值,特别是有附加条件的代数式求值问题,往往需要利用因式分解、分式的性质、倒数、韦达定理、非负数的性质等等,经过恒等变形,把代数式中隐含的条件显现出来,化简,进而求值。
一、整体代值
此类型是代数式求值问题中的基本类型,其中又蕴含了一种重要的数学方法——换元法,因此显得非常重要。
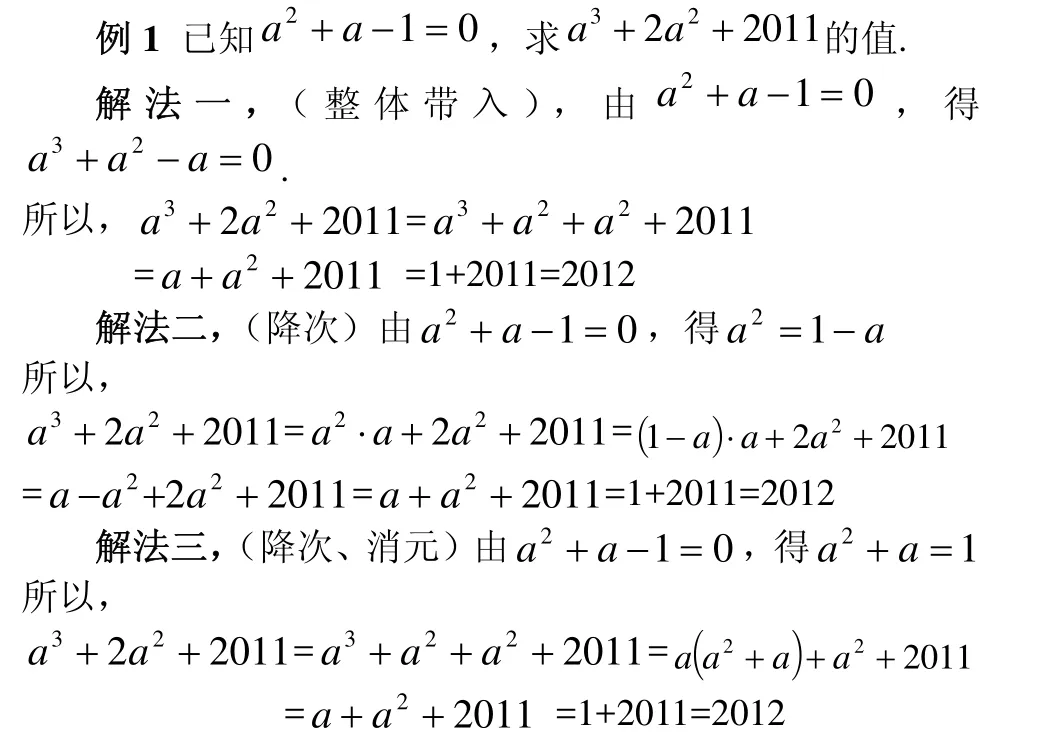
二、发掘隐含条件
适时发掘题目隐含条件,特别是有附加条件的代数式求值问题,往往需要利用实数运算性质,把代数式中隐含的条件显现出来,化简,进而求值。
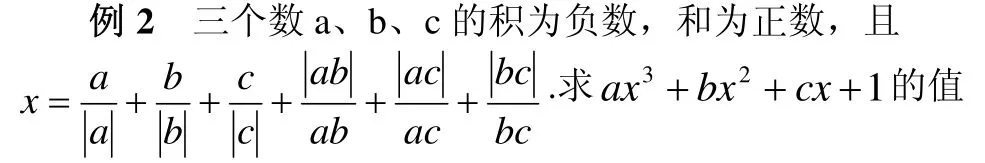
解:因为abc<0,所以a、b、c中只有一个是负数,或三个都是负数;又因为a+b+c>0,所以a、b、c中只有一个是负数.不妨设a<0,b>0,c>0,则ab<0,ac<0,bc>0故将代入要求的代数式得到结果为1.同理,当b<0 或a<0时,要求的代数式得到结果仍为1.
三、利用非负数的性质求值
若几个非负数的和为零,则每个非负数都为零,这个性质在代数式求值中经常被使用.
例3 若x2-4x+|3x-y|=-4,求yx的值.
分析:x,y的值均未知,而题目却只给了一个方程,似乎无法求值,但仔细挖掘题中的隐含条件可知,可以利用非负数的性质求解.
解:因为x2-4x+|3x-y|=-4,所以x2-4x+4+|3xy|=0,即 (x-2)2+|3x-y|=0.
得x-2=0,3x-y=0,解得x=2,y=6,故yx=62=36.
四、设参数法求值
如果代数式字母较多,式子较繁,为了使求值简便,有时可增设一些参数(也叫辅助未知数),以便沟通数量关系,这叫作设参数法.

五、利用分式、根式的性质求值
分式与根式的化简求值问题,内容相当丰富,因此这里只举一个例子略做说明。
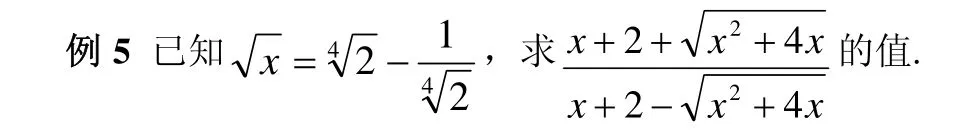
分析:计算时应注意观察式子的特点,若先分母有理化,计算反而复杂.因为这样一来,原式的对称性就被破坏了.
解:由题设知

六、利用倒数
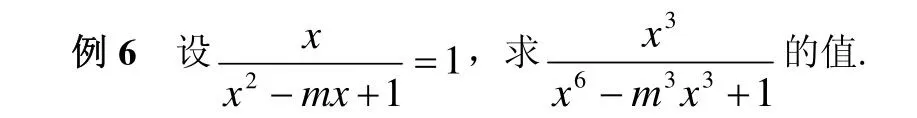
分析,两个分式比较简洁、对称,又有某些内在的联系,但分母均为多项式,不易化简求值,若利用倒数,可使问题简单化。

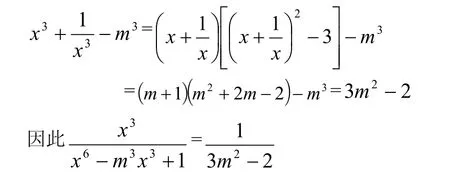
七、利用韦达定理
例7 已知实数x、y、z满足x+y=5,z2=xy+y-9,求x+2y+3z的值.

按给定条件,两个方程三个未知数,无法求出未知数的具体值。本体技巧在于运用韦达定理,找到突破口,使问题简化。
八、利用因式分解方法
因式分解是重要的一种代数恒等变形,在代数式化简求值中,经常被采用。
分析x的值虽已给出的,但直接代入求值,将会很麻烦.我们可以先将所求的代数式变形,看一看能否利用已知条件。

在求代数式的值时,若已知的是一个或几个代数式的值,这时要尽可能避免解方程(或方程组),而要将所要求值的代数式适当变形,再将已知的代数式的值整体代入,会使问题得到简捷的解答。
G424.1
A
1008-7427(2012)08-0145-01
2012-06-14
