加筋砂土挡墙面板刚度效果的数值分析
2012-11-02彭芳乐曹延波
彭芳乐,曹延波
(1. 同济大学 地下建筑与工程系,上海 200092;2. 同济大学 岩土及地下工程教育部重点实验室,上海 200092)
1 引 言
现行的加筋土挡墙设计方法往往忽略了面板刚度对挡墙承载力及变形破坏的影响。目前通常的设计方法是将加筋材料的一端与面板连接且另一端延伸至潜在的破坏面之外,以此来抵抗作用在加筋区域上的土压力,但忽略了面板刚度对加筋土挡墙的稳定性影响。Schlosser等[1]在加筋土挡墙模型试验中发现,金属面板的刚度影响了挡墙的临界高度。Jaber[2]从加筋土挡墙离心模型试验中发现,采用全高刚度面板的加筋土挡墙整体强度比分离式面板的情况大。Helwany[3]利用非线性弹性模型研究了面板刚度对加筋土挡墙的设计荷载和面板水平方向变形的影响。Onodera等[4]研究了采用3种不同面板的土工格栅加筋土挡墙的长期性能。Bathurst等[5]分别对使用刚性面板和柔性面板的两种加筋土挡墙进行了加载试验,发现与柔性面板情况相比,刚性面板可作为一种结构构件使得加筋材料承受的拉力大幅减小。Feng等[6]分别对3种不同刚度面板的土工格栅加筋土挡墙模型进行了加载试验,发现挡墙的面板刚度越大,挡墙的承载力越大,墙面的变形就越小。在国内,钟昌云等[7]利用有限元计算分析了面板对加筋挡墙稳定性的影响,发现面板刚度越大,加筋土挡墙的安全系数就越大。但以上学者的研究均没有涉及到面板刚度对加筋土挡墙的渐进性变形破坏过程的影响。
Tatsuoka及其研究组[8]分别对3种配置不同刚度面板的加筋砂土挡墙模型进行了加载试验,研究了面板刚度变化对加筋土挡墙承载力及渐进性变形破坏的影响,发现:3种加筋砂土挡墙均呈明显的渐进性变形破坏的特点,且随着面板刚度的增加,加筋砂土挡墙的极限承载力能够大幅度地提高。彭芳乐等[9-12]利用可考虑局部破坏的非线性弹塑性有限元模拟了加筋砂土地基以及挡墙的模型试验,讨论了加筋砂土渐进性变形破坏的有限元分析方法以及加筋砂土挡墙筋材层数的影响,比较合理地模拟了相关室内试验的结果。为了分析加筋砂土挡墙的面板刚度效果,本文拟采用上述可考虑应变局部化的非线性弹塑性有限元方法对Tatsuoka研究小组试验中3种配置不同刚度面板(B型面板——柔性面板,C型面板——分离式组合面板,D型面板——全高刚性直立面板,面板刚度大小:B型 图1所示为平面应变条件下加筋砂土挡墙模型试验体[8],其宽度为81 cm(不包括面板厚度),长度为39.5 cm,高度为52 cm。在砂箱中先将风干的日本丰浦(Toyoura)砂(土粒相对密度Gs=2.64,最大孔隙比emax=0.933,最小孔隙比emin=0.624)通过空中自由降落法制备砂层,通过木槌振捣使其密实(砂土相对密实度 Dr≈ 90%),并在墙后填土中铺设了10层加筋材料,加筋材料与面板刚性连接,且每层铺设长度均为15 cm,层间垂直间距为5 cm。试验所用加筋材,每层由 5根磷青铜条带(宽为0.3 cm,厚为0.01 cm)通过直径为0.05 mm的磷青铜丝相互连接而成,横向间距和纵向间距分别为5 cm和10 cm,其形状如图2(a)所示。每根磷青铜条带上粘贴有3个应变计以量测筋材的拉力,如图2(b)所示。试验在平面应变条件下,以 0.08~0.10 mm/min速率对位于挡墙顶部的刚性条形基础(宽为10 cm,长为39.5 cm,如图1所示)进行加载。条形基础中心与面板背面的距离为10 cm,位于加筋区域正上方。 图1 加筋砂土挡墙模型示意图(单位:cm)Fig.1 Sketch of reinforced-sand retaining wall model (unit: cm) 图2 试验使用的加筋材料(单位:cm)Fig.2 Reinforced materials used in model tests (unit: cm) 试验采用的3种面板分别为:①全高刚性直立型面板(D型),由11个木块通过钢筋(内部)和加固件(外部)紧密连接而成,厚度为3 cm(见图3);②分离式组合面板(C型),也由11个木块组成,面板构造及尺寸同D型面板,但木块之间没有通过钢筋紧密连接;③柔性面板(B型),为厚度为0.02 cm的描图纸。3种面板刚度大小:B型 本文计算所采用的分析软件为笔者所在研究小组自行编制的岩土工程高精度非线性有限元分析程序(软件登记号为2009SR040361)。图4为平面应变条件下采用C型、D型和E型面板的加筋砂土挡墙的有限元网格划分,其尺寸与模型试验体相同,整个挡墙填土体(砂土)和面板被划分为4节点四边形平面应变单元。对于采用B型面板的加筋砂土挡墙,其有限元网格划分与图4相同,除了面板化为一维线单元外。为了能准确地反映加筋砂土挡墙的变形与破坏现象,基础附近区域被离散化为1 cm×1 cm的四边形单元(见图4)。关于模型挡墙的边界,在左边界施加水平位移约束,在底部边界施加垂直位移约束,并在面板底部施加水平和垂直位移约束。 图3 试验使用的全高刚性直立型面板(单位:cm)Fig.3 Details of full-height rigid facing used in model tests (unit: cm) 图4 有限元网格(C型、D型和E型面板工况)Fig.4 FEM meshes(for C-type, D-type and E-type facing cases) 砂土的本构关系采用了修正塑性功硬化-软化弹塑性模型[11-14]。笔者在文献[11-14]中已经详细介绍了该本构模型及参数,此处只简单介绍该本构模型的构建框架以及特点。 该本构模型的屈服函数和势函数分别表示为Mohr-Coulomb和Drucker-Prager形式。模型以修正塑性功为硬化-软化基本参数,并与惟一对应的应力状态参数一起定义一个与应力历史和应力路径无关的的峰值前、峰值附近及峰值后的硬化-软化函数。砂土弹性特征采用了横观各向同性亚弹性模型[15]。本构模型中假定平面应变条件下砂土试样的变形在峰值前为均匀状态,在峰值附近突然发生应变局部化而产生剪切带。为了在砂土应变软化中考虑剪切带的影响,在总应变的表达式中引入一个应变局部化参数。该本构模型可以考虑砂土以下变形强度特性:①围压大小的相关性;②各向异性;③峰值前应变硬化及峰值后应变软化的非线性特性;④剪胀性;⑤应变局部化及剪切带形成特性;⑥应力历史和应力路径的相关性。 B型面板(柔性面板)采用线弹性的梁单元模拟,其弹性模量为E=10 MPa,梁单元面积A=2×10-6m2,惯性矩I=6.67×10-15m4。D 型面板(全高刚度直立型面板)采用线弹性的4节点四边形平面应变单元模拟,弹性模量为E=100 MPa。C型面板(分离式组合面板)也采用线弹性的4节点四边形平面应变单元模拟,但是没有设置界面单元以考虑木块之间的相对滑动,而是采用弹性模量折减的方式[16]考虑此种效应,经过试算得到C型面板的等效弹性模量E=1 MPa。E型面板与D型面板相同,也采用线弹性的4节点四边形平面应变单元模拟,但弹性模量为E=29600 MPa。本文采用相对刚度lg[E I/(E I)0]概念评价 4种面板刚度大小,如表1所示。 表1 面板刚度评价指标Table 1 Evaluation indices of facing rigidity 由于试验所用的磷青铜条带(见图 2)为刚性的抗拉材料,具有一定的抗弯刚度,所以本文采用线弹性梁单元对其进行模型化。该加筋条带不能直接在二维平面应变有限元中模拟,需采用面状筋材替代,此时面状筋材具有与实际加筋条带等价的刚度和材料属性。如图2所示,在室内试验中,每层加筋层中沿着ε2方向(即与磷青铜条带垂直的方向)在40 cm宽度范围内铺设了5根磷青铜条带,覆盖率CR=3%。根据等价换算得到ε2方向单位长度上模拟筋材层的梁单元面积A=2.9×10-4cm2和惯性矩I=2.4×10-9cm4。另外,根据抗拉试验测得磷青铜的弹性模量E=122 GPa。 基于试验观察,本文的解析对象加筋砂土挡墙中,砂土与磷青铜条带以及面板之间并未发生明显的滑动,并且磷青铜条带也未被拉断。因此,本文没有设定特殊的界面单元,只是假定模拟加筋材的梁单元的上、下两层砂土单元以及临近面板的左侧砂土单元为容易破坏的弱面单元[9-10]。此种弱面单元仍然遵循以上砂土的应力-应变本构关系,但与一般砂土单元相比,会较早地进入破坏阶段。 在模型试验中,通过放置在挡墙顶部的条形刚性基础以位移控制方式对加筋砂土挡墙施加集中竖向荷载,如图1所示。在进行有限元分析时,本文没有专门对基础进行有限元模型化,只是沿着加载方向在基底上节点(挡墙顶部)施加均匀的位移,没有约束节点水平方向位移,以便满足基础底部完全光滑的情况。 有限元的非线性计算采用了动态松弛法,这种方法与Newton-Raphson法相比,更加适合于具有较大内摩擦角砂土的非线性计算,可以有效地模拟砂土应力-应变关系从硬化-峰值-软化的整个过程,详见文献[17]。 首先在K0(静止侧压力系数)条件下形成初始应力场,垂直应力 σv0=γdh ,水平应力σh0=K0σv0,其中h为相应单元的高斯点距离加筋砂土挡墙顶面的深度,模型试验中砂土的干重度γd=16 kN/m3。根据文献[18]的经验方程,可以得到 K0=0.52e0,其中e0为平均孔隙比。然后以位移控制的方式在基础底部节点上(加筋土挡墙顶部)施加竖向位移,位移增量取为 0.004 mm/步。对于大部分密实加筋砂土挡墙,位移增量足够小可以保证计算的精度和稳定性。另外,计算收敛状态由两个标准判定,可参见文献[9-12]。 图5为从室内试验[8]和有限元分析得到的配置不同刚度面板的加筋砂土挡墙的基底平均压力q和基础沉降s之间的关系。图6给出了面板刚度(相对刚度lg[EI/(E I)0],见表1)对峰值承载力Nr=2q/(γdB),(B为条形基础宽度)和峰值荷载时基础相对沉降sf/B的影响。从这些图中可以看到: (1)如图5所示,对于B型、C型和D型3种工况来说,有限元计算所获得的平均应力-沉降的关系曲线呈现峰值前硬化-峰值-峰值后软化的特点,与试验结果吻合较好。因此,有限元也较好地模拟了面板刚度对加筋挡土墙的平均应力-沉降关系的影响效果。然而,有限元分析所得到的峰值承载力和峰值前初始刚度均稍大于相应试验的结果。这可能是由于加筋条带被简化为二维面状筋材模型,或砂土与加筋以及面板之间接触面单元相对简单的假设所带来误差的缘故。 (2)如图6(a)所示,随着面板刚度的增加,加筋砂土挡墙的峰值承载力也增大,尤其是D型和E型面板加筋砂土挡墙的峰值承载力显著提高。如图6(b)所示,虽然有限元所得到的峰值承载力时基础的相对沉降量比室内试验稍微偏小,但有限元计算结果基本上与室内模型试验结果一致。 图5 不同面板类型的试验与有限元p-s曲线的比较Fig.5 Comparison between tested and FEM p-s curves for different facing types 图6 试验结果与有限元结果比较Fig.6 Comparison between finite element analysis and experimental results 图7为从室内试验[8]中观察到配置不同刚度面板的加筋砂土挡墙在峰值后(s=1.5 cm)的最大剪应变γmax等值线图。从图中可以看到: (1)3种加筋砂土挡墙均出现1条从基础后端开始沿着加筋区域后端垂直向下延伸的剪切带。 (2)随着面板刚度的增加,剪切带延伸深度减小,滑动破坏面越难穿过加筋区域,这也意味着加筋区域整体性增加,加筋砂土挡墙稳定性更好。 图7 试验所得的加筋砂土挡墙在峰值后(s=1.5 cm)的最大剪应变γmax等值线图[8]Fig.7 Contours of maximum shear strain γmaxof reinforced-sand retaining walls at post-peak (s=1.5 cm)obtained from the experimental tests[8] 图8为有限元分析对配置不同刚度面板(B型、C型和D型面板)的加筋砂土挡墙在峰值前、峰值以及峰值后加载阶段下最大剪应变γmax等值线图。在相同峰值后加载阶段下(s=1.5 cm)比较室内试验(见图7)和有限元分析(见图8)得到的剪应变场,可以发现:本文所提出的有限元较好地模拟了室内试验结果,有限元分析得到的剪切带形式与室内试验结果较为吻合。除了1条从基础后端开始向面板延伸的剪切带外,还在基础前端下方出现1条垂直向下的剪切带。面板刚度越小,基础后端出现的剪切带向下朝向面板延伸与基础前端下方的剪切带相交形成的楔形体也越明显(如B型面板工况)。这也说明了随着面板刚度的增加,面板对剪切带的延伸发展的抑制作用越明显,加筋砂土挡墙的峰值承载力也越高。上述分析与比较说明,本文所建议的有限元可以较为准确地模拟影响加筋砂土挡墙的平均压力-沉降曲线及其相对应的剪切带发生发展的过程。 图9比较了室内试验[8]和有限元峰值时配置几种不同刚度面板加筋砂土挡墙中各层筋材的拉力分布。从图中可以看到: (1)对于B型、C型和D型面板3种工况,有限元较为准确地模拟了加筋砂土挡墙的各层加筋材料的拉力分布。有限元分析所得到的各层加筋材料两端处拉力与室内试验结果比较吻合,但最大拉力位于各层加筋材料中部位置附近,与试验结果有所不同,特别是D型面板的状况最为明显,这可能是有限元计算时过高地估计了中部位置加筋材和砂土之间的相互作用。 (2)随着面板刚度增加,与面板连接处加筋材的拉力依次增大。这也进一步说明随着面板刚度增加,筋材对砂土的约束围压依次增大,面板抑制砂土变形的能力也依次增大。但与C型面板工况相比,D型面板工况下与面板连接处筋材拉力的增大幅度较小(除了第2层和第8层筋材拉力增幅较大),这可能是由于两种工况下筋材发生了不同程度的滑动。但从图5和图6(a)可知,与C型面板工况相比,采用D型面板的加筋砂土挡墙峰值承载力得到显著提高。这说明了加大面板刚度虽不能大幅度提高筋材抗拉能力的发挥,但显然可以提高面板对砂土变形的抑制作用,而这个作用对提高加筋砂土挡墙的整体极限承载力是显著的。 图10为从室内试验[8]和有限元分析所得到的峰值时配置不同刚度面板加筋砂土挡墙面板的水平土压力σh/P0分布(σh为峰值时面板的水平土压力, P0为峰值时相应的基底平均压力值)。 由图10可知,有限元比较准确地模拟了3种面板工况下加筋砂土挡墙面板的水平土压力分布。在相同加载方式下,随着面板刚度的增加,面板的水平土压力的中心位置提高。这也说明面板刚度越大,面板对其附近砂土变形的抑制作用也越大。面板的水平土压力最大值基本上处于面板中下部。 图11为从有限元计算所得到的上述 B型、C型和D型面板加筋砂土挡墙中基础下部指定单元的局部应力路径。如图8所示,这些单元处于同一高度,位于基础下方加筋区域内部或者外部。图中应力路径以σ1和σ3关系表示,对应基础沉降s从0到局部峰值加载阶段(各单元处于各自峰值状态),并且给出主应力比 R=σ1/σ3对应的直线作为参考。由图11可知: (1)各工况中单元 1066、1081和 1246在整体峰值状态前达到了局部峰值状态,而单元 1048在整体峰值状态后达到局部峰值状态。该结果反映了3种加筋砂土挡墙渐进性变形破坏的特征。另外,各工况加筋砂土挡墙的基础下方区域处于明显的各向异性压缩状态。 (2)各工况中基础下方区域中的单元σ1和σ3在峰前状态下基本上按照恒定的应力比增加,且随着面板刚度的增加,位置相同的单元的主应力比R趋于相同。特别是面板刚度较大工况中(C型和D型),这种现象较为明显。这也进一步说明了面板的刚度效果实际上是通过增大砂土的围压σ3,进而提高砂土强度σ1,从而达到提高加筋砂土挡墙承载力的效果。 图8 有限元分析所得的加筋砂土挡墙在峰值前、峰值以及峰值后的最大剪应变γmax等值线图Fig.8 Contours of maximum shear strain γmaxof reinforced-sand retaining walls by finite element analysis at pre-peak, peak and post-peak 图9 峰值时筋材拉力的有限元与试验结果的比较Fig.9 Comparisons of the reinforcement tensile force at peak between finite element analysis and experimental results 图10 峰值时面板水平土压力分布的有限元与试验结果的比较Fig.10 Comparison of distribution of horizontal earth pressure on the back of facing at peak between finite element analysis and experimental results 图11 有限元分析得到的指定单元的局部应力路径(σ1-σ3曲线)Fig.11 Local stress paths of representative elements from finite element analysis (σ1-σ3curves) (1)建议的非线性弹塑性有限元方法不仅较好地模拟了加筋砂土挡墙模型试验中基础的平均压力-沉降关系,且比较合理地模拟了加筋砂土挡墙的渐进性变形破坏的现象(剪切带的发生与发展状况)、加筋材的拉力分布以及面板水平土压力分布。 (2)建议的有限元方法成功地模拟了加筋砂土挡墙的面板刚度效果,再现了由于面板刚度变化而带来的加筋砂土挡墙基础的变形破坏的影响。有限元分析表明,在相同的加载方式下,随着面板刚度的增加,面板对剪切带的抑制作用将随之增加,具体表现在砂土围压σ3增大所带来砂土强度σ1的提高,进而使加筋砂土挡墙基础的峰值承载力也随之增大。 [1] SCHLOSSER F, JURAN I. Behavior of reinforced earth retaining walls from model studies[C]//Developments in Soil Mechanics and Foundation Engineering. London:Applied Science Publishers, 1983: 197-229. [2] JABER M B. Behavior of reinforced soil walls in centrifuge tests[D]. California: The University of California Berkeley, 1989. [3] HELWANY M B, TATSUOKA F, TATEYAMA M, et al.Effects of facing rigidity on the performance of geosynthetic-reinforced soil retaining walls[J]. Soils and Foundations, 1996, 36(1): 27-38. [4] ONODERA S, FUKUDA N, NAKANE A. Long-term behavior of geogrid reinforced soil walls[C]//Proceedings of the 3rd Asian Regional Conference on Geosynthetics(GeoAsia 2004). Seoul: A. A. Balkema, 2004: 255-264. [5] BATHURST R J, VIACHOPOULOS N, WALTERS D L, et al. The influence of facing stiffness on the performance of two geosynthetic reinforced soil retaining walls[J]. Canadian Geotechnical Journal, 2006, 43(12):1225-1237. [6] FENG X J, YANG Q, LI S L, et al. The influence of facing stiffness on the performance of geogrid reinforeced retaining walls[J]. Electronic Journal of Geotechnical Engineering, 2008, 13: 1-15. [7] 钟昌云, 方玉树. 面板对加筋土挡墙稳定性影响的分析[J]. 后勤工程学院学报, 2003,19(3): 79-82.ZHONG Chang-yun, FANG Yu-shu. Analysis of the effect of the front-panel on the added reinforcing bar soil wall stability[J]. Journal of Logistical Engineering University, 2003, 19(3): 79-82. [8] TATSUOKA F, TATEYAMA M, MURATA O. Earth retaining wall with a short geotextile and a rigid facing[C]//Proceedings of 12th ICSMFE. Rio de Janeiro:A. A. Balkema, 1989: 1311-1314. [9] PENG F L, KOTAKE N, TATSUOKA F, et al. Plane strain compression behavior of geogrid-reinforced sand and its numerical analysis[J]. Soils and Foundations,2000, 40(3): 55-74. [10] 彭芳乐, 小竹望, 龙冈文夫. 土工格栅加筋砂土的变形与破坏机理解析[J]. 岩土力学, 2004, 25(6): 843-849.PENG Fang-le, KOTAKE N, TATSUOKA F. Numerical analysis of deformation and failure mechanism of geogrid-reinforced sand[J]. Rock and Soil Mechanics,2004, 25(6): 843-849. [11] 彭芳乐, 曹延波. 加筋砂土挡墙承载力及渐进性变形破坏的有限元分析方法[J]. 岩石力学与工程学报, 2011,30(增刊 2): 3703-3713.PENG Fang-le, CAO Yan-bo. FE analysis method on bearing capacity and progressive failure of reinforced-sand retaining walls[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Supp. 2):3703-3713. [12] 彭芳乐, 曹延波. 加筋砂土挡墙筋材层数影响的有限元分析[J]. 岩土工程学报, 2011, 33(11): 1700-1707.PENG Fang-le, CAO Yan-bo. FEM analysis of effect of reinforced layer numbers on reinforced-sand retaining walls[J]. Chinese Journal of Geotechnical Engineering,2011, 33(11): 1700-1707. [13] 彭芳乐, 白晓宇, 谭柯, 等. 基于修正塑性功函数的砂土硬-软化本构模型[J]. 同济大学学报(自然科学版),2009, 37(6): 720-726.PENG Fang-le, BAI Xiao-yu, TAN Ke, et al. An elasto-plastic constitutive model with hardening-softening behavior for sandy soil based on modified-plastic work state function[J]. Journal of Tongji University (Natural Science), 2009, 37(6): 720-726. [14] PENG Fang-le, SIDDIQUEE M S A, TATSUOKA F, et al.Strain energy-based elasto-viscolastic constitutive modeling of sand for numerical simulation[J]. Soils and Foundations, 2009, 49(4): 611-630. [15] HOQUE E, TATSUOKA F. Anisotropy in the elastic deformation of materials[J]. Soils and Foundations,1998, 38(1): 163-179. [16] YOO C, KIM S B. Performance of a two-tier geosynthetic reinforced segmental retaining wall under a surcharge load: Full-scale load test and 3D finite element analysis[J]. Geotextiles and Geomembranes, 2008,26(6): 460-472. [17] TANAKA T, KAWAMOTO O. Three-dimensional finite element collapse analysis for foundations and slopes using dynamic relaxation[C]//Proceedings of Sixth International Conference on Numerical Methods in Geomechanics. Innsbruck: Balkema A. A., 1988: 1213-1218. [18] OKOCHI Y, TATSUOKA F. Some factors affecting K0-values of sand measured in triaxial cell[J]. Soils and Foundations, 1984, 24(3): 52-68.2 模型试验与有限元模型
2.1 试验概况
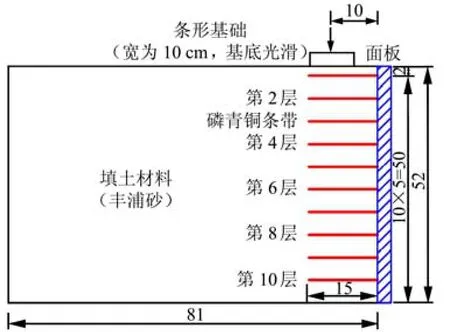

2.2 有限元网格
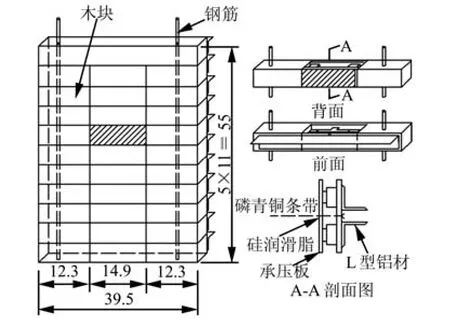
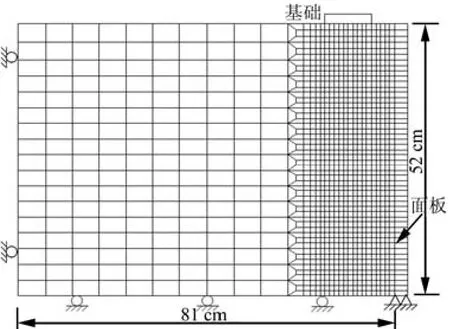
2.3 砂土的本构模型
2.4 面板的模型化

2.5 加筋材、界面单元及基础的模型化
2.6 有限元计算分析步骤
3 结果与讨论
3.1 基础底面平均压力-沉降关系的比较与分析
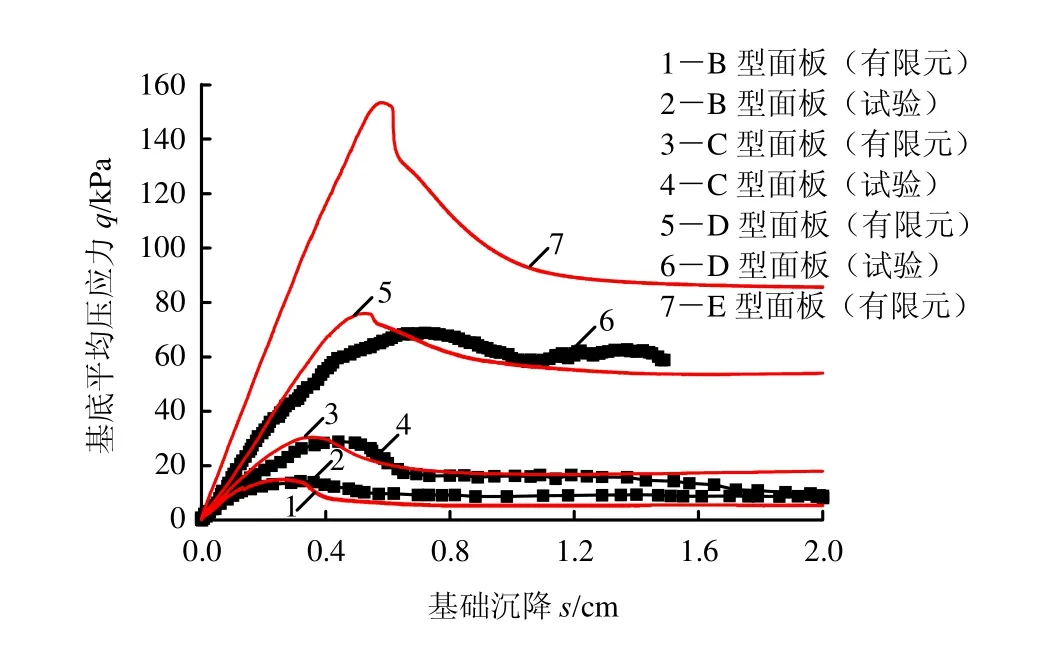

3.2 应变场与剪切带

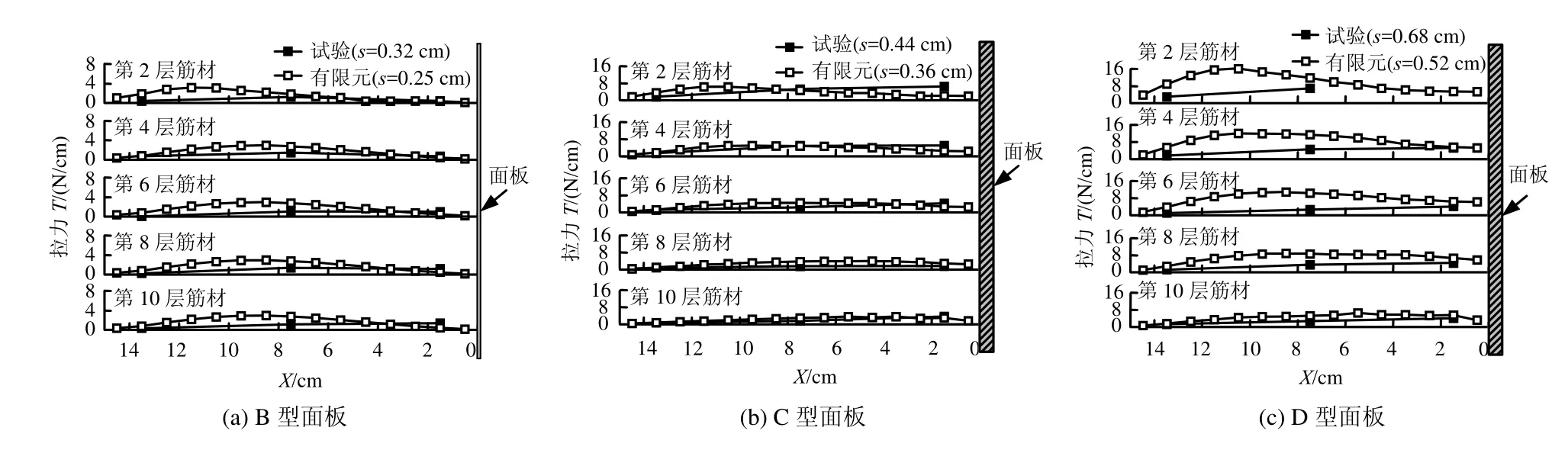
3.3 筋材的拉力
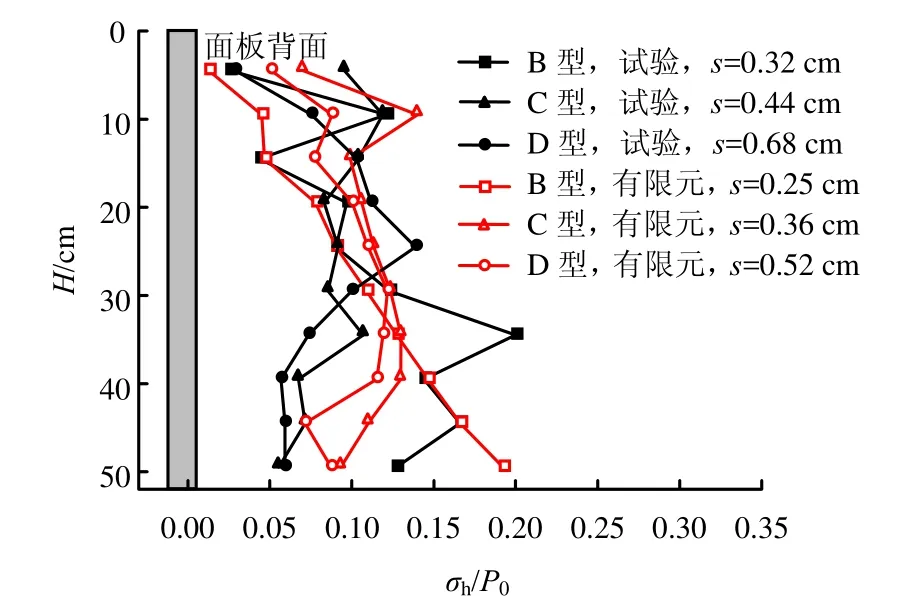
3.4 面板水平土压力分布
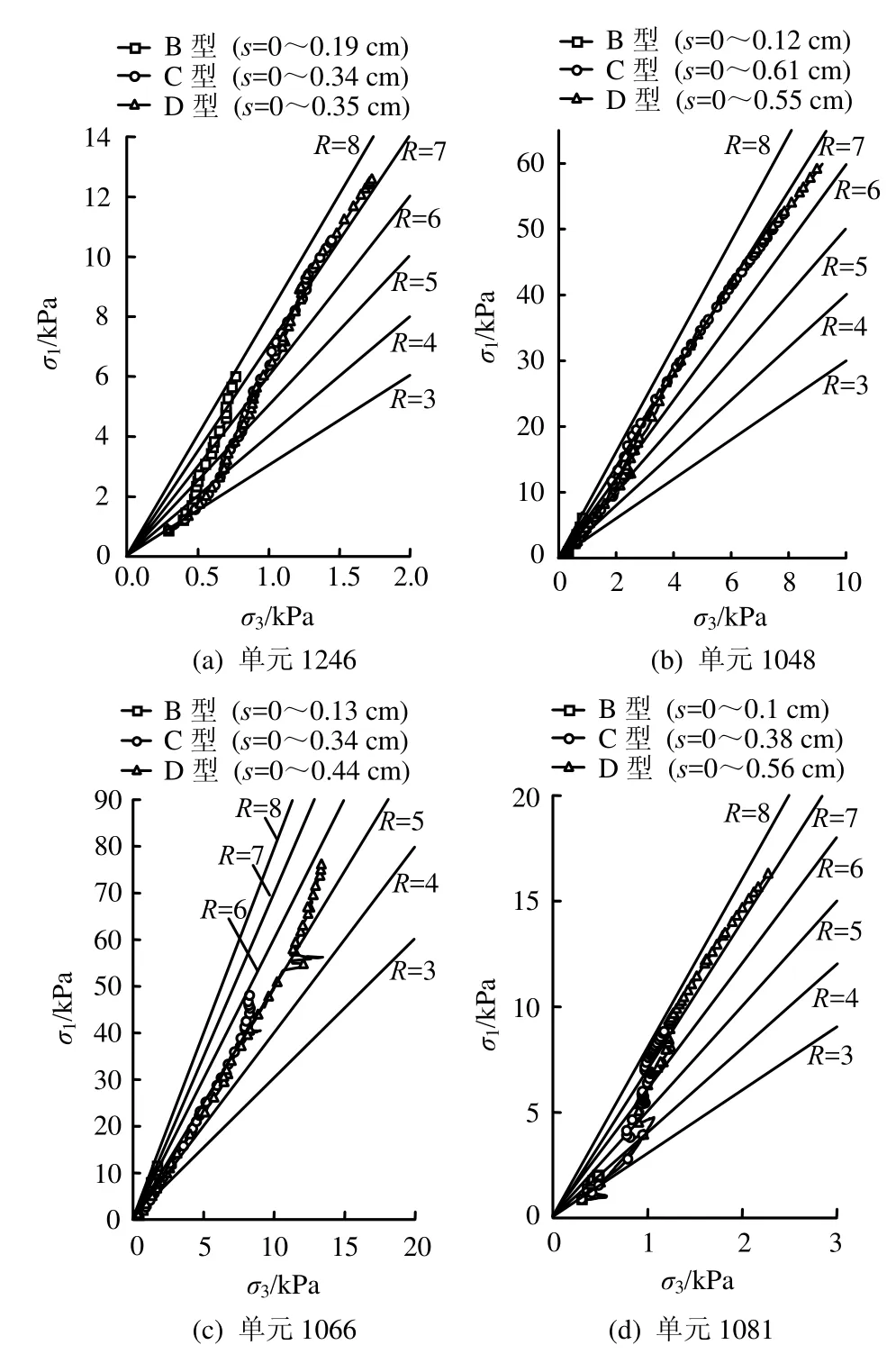
3.5 局部应力路径

4 结 论
