H-矩阵的一组充分条件

杨亚芳，梁茂林

（天水师范学院 数学与统计学院，甘肃 天水 741001）

1 引言及预备知识

非奇异H-矩阵有着广泛的应用，许多实际问题都可归结为求解大型线性方程组，而在求解方程组时往往假设其系数矩阵是非奇异H-阵，这是因为当迭代矩阵是非奇异H-阵时，Jacobi，JOR，SOR，SSOR都是收敛的，因此判别一个矩阵是否为H-阵有着十分重要的意义.文献［1-4］等给出了简单实用的判别条件，本文给出了一组新的有效判别条件.

设Mn(C)表示n阶复方阵的全体，A∈Mn(C)，记

令

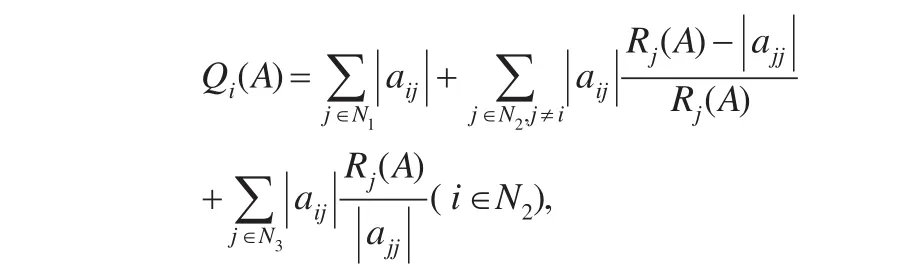
定义1.1[5]若A∈Mn(C)满足且至少有一个严格不等号成立，对于每一等式成立的i或N3中的i使得非零元素链aij1aj1j2…ajk-1jk满足则称A为具有非零元素链的对角占优矩阵.熟知具有非零元素链的对角占优矩阵是非奇异H-矩阵.

2 主要结论

定理2.1若A∈Mn(C)满足

则A是非奇异H-矩阵.

证明 由（1）式和（2）式知

因此一定存在充分小的ε＞0满足

构造正对角矩阵D=diag(d1，d2，…，dn)，其中

记B=AD，下面证明B是严格对角占优矩阵.

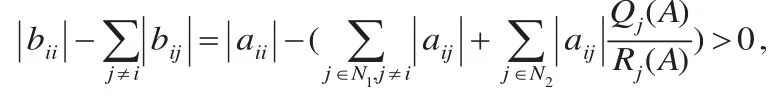
对任意的i∈N2， 当时，由（6）式得

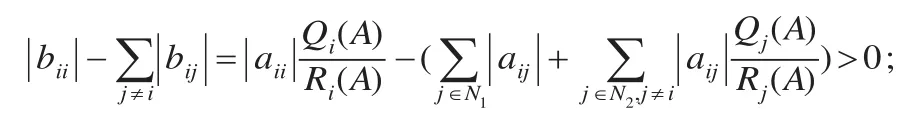
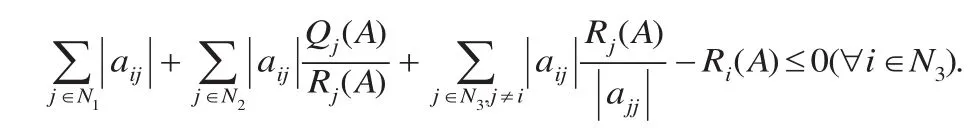
从而

由ε的非负性知

所以对任意的i∈N3，

所以B为严格对角占优矩阵，即A为非奇异H-矩阵.

定理2.2设A∈Mn(C)为不可约矩阵且满足

且上述式子中至少有一个严格不等号成立，则A是非奇异H-矩阵.

证明 构造正对角矩阵D=diag(d1，d2，…，dn)，其中

记B=AD，下面证明B是严格对角占优矩阵.

对任意的i∈N1， 由（7）式知

对任意的i∈N2， 由（8）式知

且存在i∈N1∪N2， 满足

所以B为不可约对角占优矩阵，即A为非奇异H-矩阵.

定理2.3设A∈Mn(C)，如果满足

且上述式子中至少有一个严格不等号成立，对于每一等式成立的i或N3中的i，存在非零元素链满足当k∈N1时，

或当k∈N2时，

则A是非奇异H-矩阵.

3 数值例子

设

则N1={2}，N2={3}，N3={1，4}，Q3(A)=11.5833 ，

即由定理2.2知A为非奇异H-矩阵.因为

所以不能用文献［2］判断.又因为

所以不能用文献［3］判断.

[1]VARGE R S.On recurring theorems on diagonal dominance[J].Linear Algebra,Appl.,1976,(13):1-9.

[2]BERMAN A,PLEMMONS R J.Nonnegative Matrices in the Mathematical Sciences[M].Philadelphia:SIAM Press,1994.

[3]逄明贤.矩阵对角占优性的推广及应用[J].应用数学学报,1989,12:35-33.

[4]黄廷祝.非奇异H-矩阵的简捷判据[J].计算数学,1993,15:318-328.

[5]胡家贑.线性方程组的迭代解法[M].北京:科学出版社,1991.