配电网的回路阻抗法潮流计算与仿真可视化
2012-10-30王文举李光耀
王文举,李光耀
(同济大学 电子与信息工程学院,上海 201804)
潮流计算是电力网络运行分析的基础,可为电力系统运行人员进行电力系统网络重构、故障处理、无功优化和状态估计提供参考依据,在电网调度、运行分析、操作模拟和设计规划中都发挥着重要的作用[1-2].
因配电网在结构上具有闭环结构、开环运行的特性,稳态运行时多呈辐射状,在发生故障或倒换负荷时则呈短时环网运行结构;且具有在线路参数上R/X(电阻/阻抗)较大,网络的PQ(P 为有功率,Q为无功率)节点多、PV(V为电压幅值)节点较少等特点,使得传统的、面向环状结构高压输电网进行潮流计算分析的牛顿拉夫逊算法[3]、快速解耦[4]等方法出现病态收敛,不再有效.为此,许多学者从上世纪90年代开始对配电网潮流计算进行了深入研究:一方面针对配电网结构特性对牛顿法[5]、快速解耦法[6]改进,但造成求解复杂化,失去了原有算法的收敛性和稳定性;另一方面陆续提出前推回代类算法[7-8]、回路阻抗法[9]等新配电网潮流计算方法.
前推回代类算法具有线性收敛、鲁棒性好、求解速度快、内存占用少等优异特性,但应用于环状或含有PV节点的配电网潮流计算分析时,需进行特殊处理,从而增加了求解难度,其通用性、收敛性不强.
与上述算法相比,Goswami[9]等人提出的回路阻抗法,具有网孔处理能力强、收敛性好、稳定性高、适用范围广等优点.但在计算机求解过程中存在下述问题:① 为利用稀疏矩阵技术简化回路阻抗矩阵的LU(lower-upper)分解,文献[9-10]将配电网树状结构转化成标准二叉树形式优化节点编号,加大了算法复杂度,限定了中间节点状态的求解顺序,改变了配电网原有的网络结构,不便于网络重构;文献[11]提出以邻接表与二叉树结合的方式优化节点编号,便于网络重构,但也无法进行有环配电网阻抗矩阵的自动化生成.②CPU对阻抗矩阵进行LU分解时,文献[12-13]采用一定的技巧,对对角线元素和相邻元素进行了优化,但因阻抗矩阵为对称满秩矩阵,在计算过程中矩阵元素仍将占用大量内存,计算速度会随着节点数目的大量增加而大幅下降.
此外,电网潮流计算仿真结果通常以文本或二维图表的形式给出.虽然近年来已出现基于物理拓扑结构的二维饼图、三维柱状图的表征形式[14-15],但一般用点状或线状等抽象符号表达电力设备,无法客观、真实地反映与刻画复杂的三维空间对象本身结构和相互之间的关联关系,也缺乏动态处理和时空分析的能力,存在很大的局限性.
针对上述工作的不足,笔者基于配电网回路阻抗法原理及配电网接线特点,提出了一种配电网潮流计算和仿真信息可视化的新方法,以快速、有效地模拟仿真配电网运行状况:采用十字链表对配电网物理拓扑结构进行存储,定义反映各节点之间电流流向关系的关联矩阵,在两者的基础上,设计了阻抗矩阵生成算法,用于有环、无环配电网阻抗矩阵中各元素的自动化计算,可以任意顺序计算各支路电流、内节点电压;提出了基于right-looking LU分解法的并行高斯消去算法,利用GPU(graphic processing unit)对回路阻抗矩阵快速精确求解;结合GIS和虚拟现实技术,实现了仿真运算结果信息在三维GIS(geographic information system)系统中的可视化展示.
1 回路阻抗法求解原理
配电网的基本单元是馈线,每条馈线以辐射型网络连接若干台配电变压器.如果将节点负荷用恒定阻抗表示,且不考虑配电线对地电容,并将中间变压器等值化简(其数学模型网络结构如图1所示),则从馈线根节点起到每1个负荷节点都形成1条回路.以每条回路电流为所求解变量,根据基尔霍夫电压定律,具有m个节点、n个负荷节点的配电网回路电流方程组可写为

图1 配电网数学模型Fig.1 Mathematic model

式中:VS为根节点电压;Ii为流经负荷节点vi的第i条回路电流;Zi,i为vi与VS之间的支路阻抗和加上负荷节点vi自身的负荷阻抗Zi,称为负荷节点i的自阻抗;Zi,j为负荷节点vi和vj到VS的共同支路阻抗相加之和,称为vi和vj的互阻抗[9].
当配电网只有一个vi且在该处形成闭环结构时,其环路如图2a所示.设ip1,ip2为独立的2条回路(p1,p2)的电流,Zcom为2条回路的共同支路阻抗,Zload为vi的负荷阻抗,根据KVL定律(基尔霍夫电压定律,Kinhhoffs Voltage Law),该闭环结构电路回路方程可写为
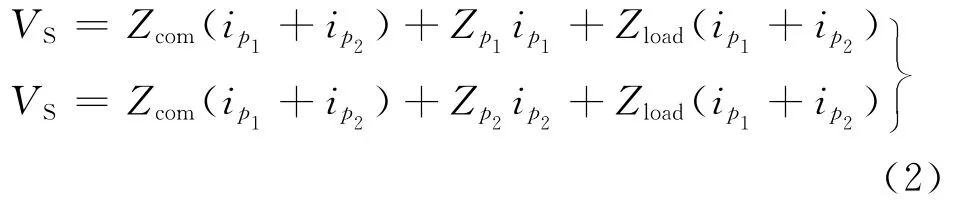
此时,需将该环在vi处解开分成2条独立的支路(图2b)求解.整理上式,写成以ip1,ip2为求解变量的方程组如下:


图2 弱环节点电流计算Fig.2 Equivalent loop of meshed network
当配电网有多负荷节点在负荷节点vi处形成弱环时,由式(1),(3)可推导出下式:
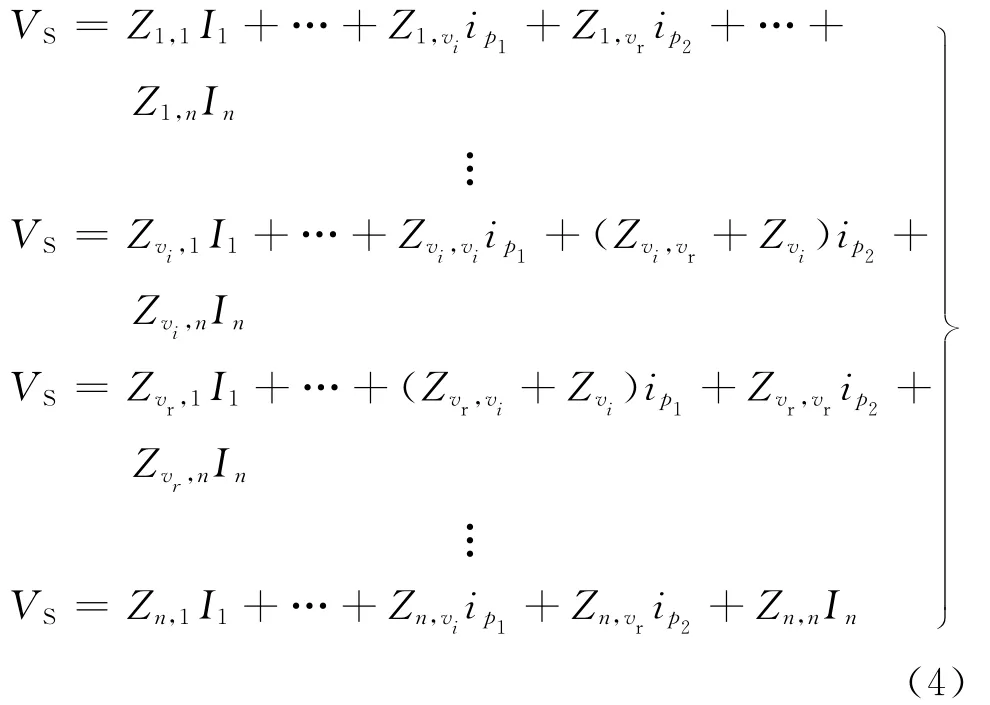
式中:Zvi,vr+Zvi可简记为Zvi,vr;Zvr,vi+Zvi可简记为Zvr,vi,且两者值相同;vr为vi破环后对应的虚拟节点.这样,回路阻抗方程组增加1阶.同理,若配电网在多个负荷节点形成多个环网,均可写成式(4)形式,但实质上已转化为式(1)形式求解.
2 潮流计算的自动化、快速求解
2.1 阻抗矩阵的自动化生成
回路阻抗法潮流计算自动化求解的核心是阻抗矩阵自动化生成,实现的前提是找到一个灵活的数据结构,能对配电网的物理拓扑进行存储,易于配电网物理状况的判断和结构调整.
2.1.1 十字链表的物理拓扑结构存储
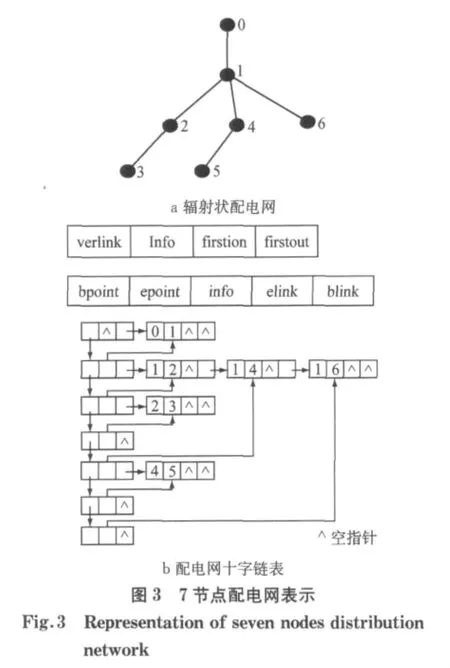
配电网在正常运行情况下呈辐射状结构;在故障处理倒负荷操作或网络重构情况下呈现短时间的环网结构.这两类拓扑结构都可以用有向图表示.有向图的存储方法主要有邻接矩阵法、邻接表法、十字链表法.邻接矩阵法占用空间大;邻接表法具有修改简单、存储方便的特点,调整较少的支路和节点信息即可实现配电网网络重构,但难以判断是否有环网生成;十字链表是邻接表法和逆邻接表法结合起来得到的一种链表,不仅继承了邻接表法的优点,而且能根据逆邻接表更易判断出构成环网结构的负荷节点,便于破环后潮流计算的求解.为此采用十字链表对复杂配电网物理拓扑结构进行存储.
考虑到配电系统的结构特点和潮流计算的需求,对十字链表相应改进:配电网中的每个节点、每条支路在十字链表中都有一个顶节点、边节点类型的存储节点相对应.顶节点由四部分组成:“verlink”为指针,指向下一顶为数据域点;info为数据域,用于对vi、负荷节点标识flag、负荷节点阻抗值Zi、闭环负荷节点破环后增加的vr等数据信息的存储;“firstin”为指针,指向第一个以该点为终点的支路;firstout为指针,指向第一个以该点为出发点的支路.边节点由五部分组成:bpoint指针和epoint指针指示支路的出发点和终点,info存储支路阻抗,elink为指针指向终点相同的下一条支路,blink为指针,指向出发点相同的下一条支路.
在构建十字链表前,需在配电网原始接线图上进行一次节点编号且编号方案任意(保证电源节点编号为零,其他节点无遗漏即可),此后再也无须额外的节点优化编号.在根据节点数目构建十字链表后,还需按照节点编号由小到大的顺序依次填充所设置的十字链表.对于顶节点,若为负荷节点,置负荷节点标识flag=vi(负荷节点编号)、vr=0,同时记录负荷节点阻抗值Zi;若为内节点,上述参数统一设置为零.对于各边节点,记录以l为起点、k为终点的支路阻抗Zl,k,完成十字链表的初始化.
当配电网络物理结构改变重构网络时,只需在记录其物理拓扑结构的十字链表中添加或删除顶节点、边节点,并改变相关指针指向即可.现以7节点系统为例说明在十字链表上的网络重构过程.图3a为配电网络原始接线方式,对所有节点编号,编号顺序任意;图3b为其对应的十字链表.当接入2~5支路构成环网时,需新建一边节点(2,5);修改v5顶点的firstin指针指向(2,5)边节点;v2顶节点所连接的(2,3)边节点的blink指针指向(2,5)边节点,同时,(2,5)边节点的elink指针指向(4,5)边节点.
2.1.2 关联矩阵
生成节点阻抗矩阵的关键是构建关联矩阵,使方程组中节点阻抗矩阵中的元素Zi,j与各输入支路阻抗、节点负荷阻抗建立起正确的对应组合关系.
从图1看出,若有n个节点,除去根节点(表示配电网供电电源)后,则有n-1个节点、n-1条支路,其支路编号可记为支路电流流入支路末端节点的节点编号.
根据配电网各节点之间的电流流向关系,参照文献[12]对关联矩阵重新定义使之更易理解和应用:关联矩阵A为(n-1)×(n-1)阶矩阵,i,j对应于除去根节点以外的节点编号,当存在流入节点j的电流且流经节点(支路)i时,Ai,j=1,否则 Ai,j=0.表1即为图3a所对应的关联矩阵.
2.1.3 阻抗矩阵的建立与修改
假定每一负荷节点处为一个两端网络,其阻抗为R+jΩ,则

其中:有功功率P=|U||I|cosφ;无功功率Q=|U||I|sinφ;|U|,|I|,φ分别是网络两端口处U,I的模和两者的相角差.若已知vi的P,Q,U,则

同时,假定U=1.0+0j,则vi的初始阻抗Zi=R+j Ω=cos2φ/P+j sin2φ/Q.
由十字链表、关联矩阵可构建包含除供电电源之外的所有配电网负荷节点的初始阻抗矩阵Z,用于第一次算法求解.Z为一复系数对称矩阵,由对角线元素Zi,i和非对角线元素Zi,j构成.


当j是i的虚拟节点编号vr时,

Zi,vr可由式(9)计算.Ak,i是关联矩阵的k 行i列元素,Zl,k是十字链表中起点为l、终点为k的支路阻抗.
以上是结合十字链表与关联矩阵提出的一种阻抗矩阵生成算法.无论配电网是否由环网构成,该算法都能完成阻抗矩阵元素的自动化计算.该算法主要包括判断是否由环网构成和阻抗矩阵元素计算两个步骤:① 判断是否由环网构成:依次遍历十字链表中顶节点,根据负荷节点标识flag≠0访问其中的负荷节点.若每一负荷节点的firstin指针所指支路的elink指针均为null,则可判定该配电网无环网构成;若某一负荷节点vi的firstin指针所指支路的elink指针不为空,则可判定在该负荷节点处形成闭环.则将其info数据域中的闭环负荷节点破环后增加的虚拟节点编号vr=h++(h=N-1,N为配电网节点总数),并在关联矩阵中添加关于vr的行和列,并调整关联矩阵中的元素值.② 阻抗矩阵元素计算:依次遍历十字链表中的负荷节点,若无环网构成,根据式(7),(9)依次计算阻抗矩阵中关于每一负荷节点的回路方程系数,直至所有负荷节点被访问完毕即可生成阻抗矩阵;若在vi处有环网生成,则根据式(7),(10),(9),(8),(10),(9)顺序,先后计算关于vi,vr的回路方程系数,其他节点的回路方程系数仍由式(7),(9)完成.随着负荷节点遍历结束,初始阻抗矩阵也就生成建立.
2.2 基于GPU的回路阻抗方程组求解
长期以来,GPU一直局限于处理图形渲染的计算任务,通过在硬件上增加并行处理单元和存储控制单元的方式,具备了同代CPU无可比拟的强大并行运算能力和高内存读写带宽.尤其是2007年,NVIDA公司的统一计算架构(compute unified device architecture,CUDA)的推出,使GPU具有更好的可编程性,可广泛用于图形渲染以外领域的计算.与传统的并行计算技术相比,基于GPU的并行计算具有低成本、高性价比的显著优势.
从式(1)看出,基于回路阻抗法的配电网的潮流计算可以归结为求解一组复系数线性方程组,其矩阵表达式为B=Z|VS(B 是n×(n+1)矩阵,n是负荷节点的数目),是一种高密度数据运算,适用于GPU快速求解.
2.2.1 CUDA编程模型
在CUDA编程架构下(如图4所示),一个应用程序分为主机(host)端和设备(device)端两部分:主机端是指在CPU上可执行的部分,设备端是在显卡上执行的部分,其中,运行在GPU上的并行计算函数称为内核(kernel)函数.在程序运行过程中,主机端程序准备好数据并复制到显存中;设备端程序执行主机端设置的一个个内核函数,每个内核函数都将按照线程网格的概念在GPU上运行(每个线程网格可包含多个线程块,每个线程块可包含多个线程,同一线程块内的线程可通过共享存储器(shared memory)通信、同步);尔后,主机端程序从显卡内存中取回运算结果[16].
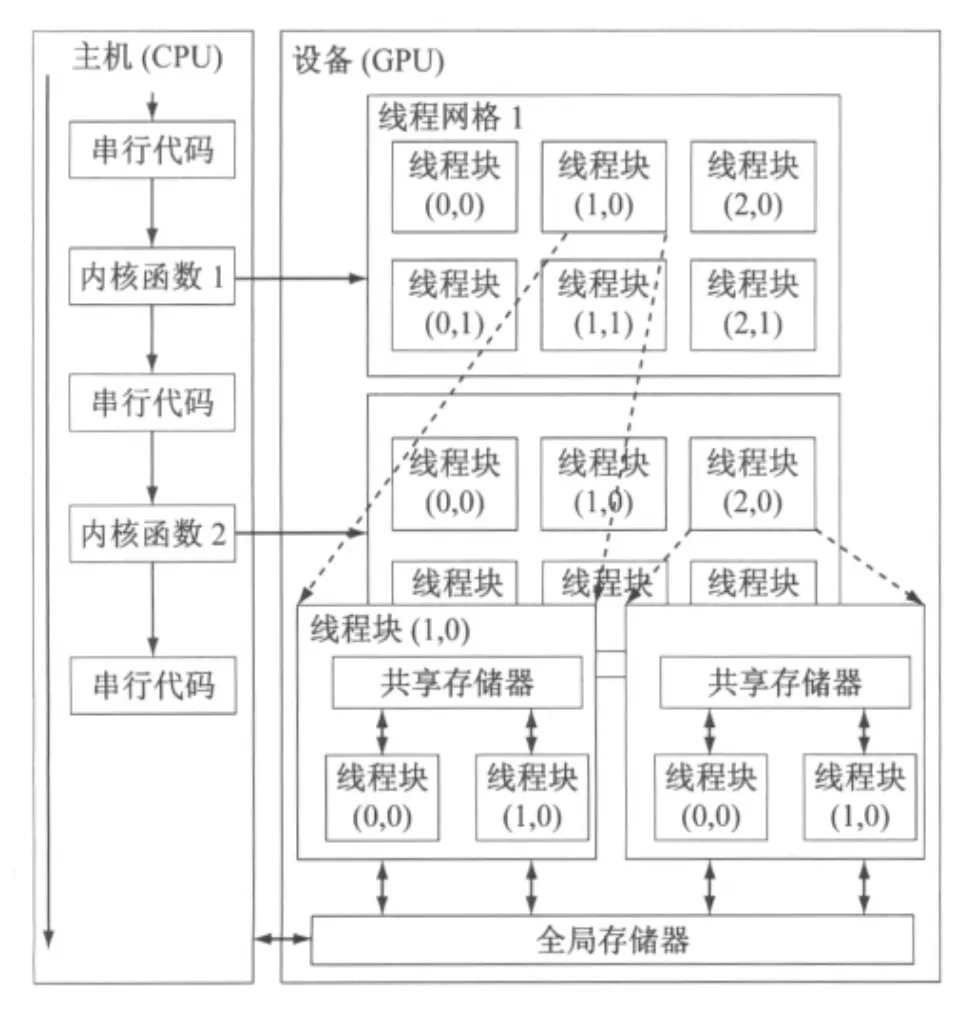
图4 基于CUDA的编程模型结构Fig.4 CUDA programming model
2.2.2 基于CUDA的复系数线性方程组求解
求解线性方程组的方法有两大类:直接法和迭代法.迭代法速度快,但有误差;直接法准确、可靠,具体有LU分解法和高斯消元法.从本质上讲,LU分解法是高斯消元法的一种变相表达形式,实质上是将矩阵通过初等行变换变为1个上三角矩阵,变换矩阵是其单位下三角矩阵的过程.LU分解算法多,根据数据的访问模式不同,可划分为left-looking和right-looking两类算法.left-looking算法是:每次迭代运算先计算矩阵中的1列各元素值,后对该列元素调整.求解过程不仅与当前列的左边矩阵中的部分元素相关,而且各元素之间也存在计算依存关系,难以并行处理.right-looking算法是:每次迭代运算先计算矩阵中的1列,再用该列中的元素去计算该列右边的子矩阵的各元素值.其求解计算不相关,可并行处理[17].
为此,笔者根据right-looking算法可并行处理的特性,结合CUDA编程模型以及复系数矩阵的结构特点,提出了基于right-looking LU分解法的并行高斯消去法(如图5所示),将大量计算集中于GPU处理,充分发挥其并行运算的能力,将回代过程减为一次,在保证求解精度不变的情况下使求解速度大为提高.

图5 基于right-looking LU分解法的并行高斯消去算法Fig.5 Parallel Gaussvan elimination algorithm based on rightlooking LU factorization
在LU分解法求解过程中,选取绝对值大的元素作为主元是确保矩阵算法稳定求解应用最广泛的技术,其中列主元法是其最常用的方法[18].这一处理过程在一般LU分解算法中是一个必不可少的环节.但在配电网潮流计算的直接求解法所形成的阻抗矩阵中,Zi,i>Zj,i,在完成第(i-1)步迭代运算过后,第i列元素中的在该列的第i行之后的所有元素中绝对值始终最大.故这一矩阵置换选取列主元的步骤在本配电网潮流计算算法中可省略,节省了大量的运算时间.
在算法流程设计中,GPU上主要进行主列元上各元素和子矩阵中各元素的并行计算,可按照CUDA编程规则分别编写对应的核函数column_element()和submatrix_element()以实现,每个核函数由多个线程并行完成.在主列元的各元素求解计算时,安排每个线程计算1个元素值;而在子矩阵各元素的求解计算时,让每个线程来计算子矩阵中1列元素值.这是因为如果用每个线程来计算1个元素值,则所需的线程数将超越1个块所允许使用的最大线程数.而在CUDA中有一硬件特性:同1块中的线程均可在同1个流多处理器中同步执行相同的指令序列,且可共用共享存储器,明显提高运算速度.
为表述算法方便,在算法流程图5中,用Bi,j来表示复系数矩阵中的某一复数元素,但在实际编程过程中,用 Ri,j,Ii,j对应其实部和虚部(即用与矩阵B同等阶数的矩阵R和I来描述复数矩阵B).因为每个块的共享存储器大小为16~64kbit,通常情况下难以将R,I整体读入共享存储器,但在每次循环计算时,可将主元列和主元列上第1个元素的同行元素从全局存储器上读入共享存储器,而R和I存于全局存储器,以此充分发挥共享存储器的访问速度远比全局存储器快得多的优势,从而减小通信延迟、提高数据访问效率.
随着2个内核函数分别调用N-1次,整个LU分解过程结束,但还需由CPU调用函数back_substitution( )回代计算,才能完成对复系数线性方程组的求解.
2.3 支路电流、内节点电压计算
经第一次GPU求解可得到各负荷节点电流,如果负荷节点功率不满足给定的精度要求,则需按式(6)对自阻抗Zi,i中的Zi调整.随之,式(1)和(4)也需对Zi,i重新赋值,然后迭代求解下一次的GPU,直至满足精度要求.然后,利用所得负荷节点电流计算配电网各支路电流、内节点电压,分别以Ii′,Uj′标识,i′,j′为内节点编号.根据基尔霍夫定律和所定义的关联矩阵与十字链表,可分别推导出它们的计算式

当j′为负荷节点时,可由式(1)迭代计算得到Ij′;Ii′,Uj′中的各值可按任意顺序求解.
3 仿真信息可视化
信息可视化是指利用计算机技术,对抽象数据进行交互与可视化,以提高人的认知功能[19].其相应的可视化技术有二维表格、三维图、几何变换技术、层次技术等几大类[20],但缺乏时空分析能力.因此,将GIS和虚拟现实技术相结合,用于进行潮流计算仿真信息可视化,使仿真抽象结果在三维虚拟空间相关实体设备上得以具体、直观地体现;从三维角度全面反映仿真配电网的运行状况,从而有助于调度人员的分析决策和培训人员的学习理解.
3.1 基于GIS技术的配电网三维仿真系统
实现三维GIS系统开发的软件工具有IMAGINE VirtualGIS, ArcGis 3DAnalyst,GeoMedia Terrain,PAMAP GIS Topographer,Java与Vrml,Creator与Vega Prime,前四个主要用于三维地理环境的分析与浏览,后两类软件组合可用于基于GIS系统的视景仿真.在最后一类软件组合中,Creator软件具有强大的多边形三维建模能力,大面积地形精确生成功能,拥有针对实时应用优化的openflight模型数据格式;Vega Prime支持Creator模型文件,提供众多附加仿真功能模块,迅速创建、渲染各种实时交互的三维仿真环境.为此,选取上述两款软件进行3DGIS动态视景仿真开发.
实现过程见图6.首先,使用Photoshop对谷歌地球卫星图片裁剪,然后在creator terrain pro模块中完成地形建模并以*.mft格式存储;建筑物建模过程较为复杂:先要搜集各建筑物图纸,在autocad软件中提取出需要的建筑物现状图,后以.dxf文件格式导入creator软件中,用face工具进行地物匹配、geometry工具设置建筑物高度,并用裁剪后的实物照片映射纹理;对于配电网电力设备、花草、树木等其他要素建模,可根据所采集的实物照片在Creator软件中直接进行;这两个所建模型均以*.flt格式存储.此后,根据实际建筑物和其他要素在三维地理空间中的位置关系,在Vega Prime软件lynx prime场景编辑器中,将上述*.flt和*.mft模型合成,设置生成*.acf文件格式存储.最后,在.net vc环境中调用Vega Prime API接口函数读取*.acf文件,并根据潮流计算结果编程设置,实现视景驱动和仿真信息可视化.

图6 3DGIS潮流计算仿真信息可视化Fig.6 3DGIS power flow calculation simulation information visualization process
3.2 潮流计算结果可视化显示
在实际电力生产作业中,运行人员通过读取配电网各变电站一次设备的仪表指示器来检测配电网的运行情况.如今,三维虚拟现实技术提供了这样的技术条件,可使使用人员在能够反映真实场景的虚拟环境中模拟观测,使实习者与管理人员将潮流计算中各节点的计算结果与监测其变化的实体设备仪表一一对应起来,从而深刻理解电网运行原理,提高业务能力.其中,仪表指针读数和控制该仪表的信号数据之间的参数转换公式为

配电网虚拟设备仪表的指针读数可视化显示通过自由度(degrees of freedom,DOF)计算机动画技术实现.该技术主要包括DOF节点设置和DOF节点驱动两个步骤.DOF节点设置在Creator中完成,DOF节点动画特效在Vega Prime中触发.在该项技术中,设置成DOF的节点可控制它的所有子节点在设置的自由度范围内移动或者旋转,运动范围由局部坐标系来指定.真实场景中当设备仪表读数变化时,其物理表现形式是仪表指针绕着指针轴旋转.因此,在Creator中首先建立一个以指针轴与指针链接处为局部坐标系原点中心的DOF节点,然后仪表指针作为它的子节点,同时设置满刻度量程旋转的角度.在潮流计算结束、用户进入3DGIS配电网虚拟环境时,由在Vega Prime视景驱动软件中的编程语句rotate(仪表指针读数)触发旋转效果.
从潮流计算的结果来看,配电网能量分布细化到了最底层的变压器一级.而现实世界中,此类设备并不配置测量仪表,所以,在3DGIS虚拟环境中就无法直观表征其数值变化.此外,为方便用户精确了解设备运行状态,此类虚拟设备旁边均设文字说明.
4 实验结果与讨论
本算法在一台Intel Core2Quad Q95502.8 GHZ CPU,3GB内存,Nvidia GeForce GTX480显卡的PC机上实现了配电网多种节点类型设置的潮流计算与仿真信息可视化,使用Visual 2005作为软件开发平台,CUDA SDK 3.2作为GPU程序的主要开发工具,Vega Prime作为3DGIS仿真可视化工具.
4.1 潮流计算算例
基于文献[9]和本文所提方法,通过编程,分别实现了基于CPU和基于GPU并行计算的配电网潮流计算程序,并采用文献[9,11,21]提供的6,20(包括环网),45,33负荷节点数的配网系统原始数据以验证本算法的高效性.在达到10-5级的计算精度条件下,两类求解算法单次收敛所需的迭代次数和100次运算花费时间对比如表2所示.
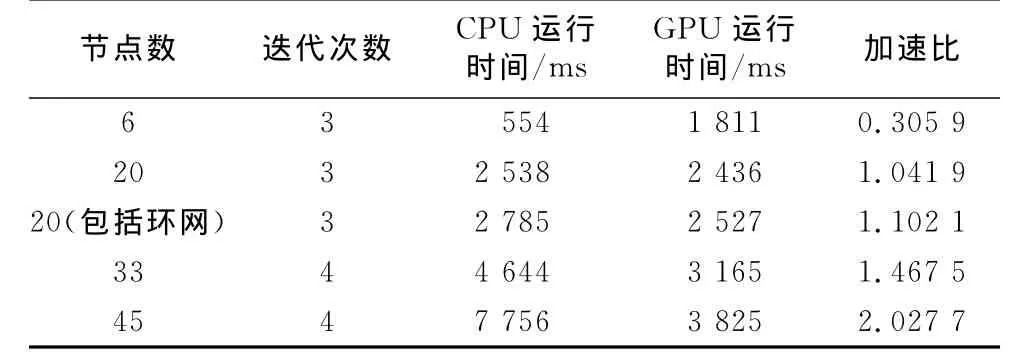
表2 CPU串行与GPU并行求解算法比较Tab.2 Comparison between CPU serial algorithm and GPU parallel algorithm
表2数据显示,本方法对无环、弱环配电网潮流计算都能快捷、精确求解.尤其是采用GPU后,在达到CPU串行求解同等精度条件下,加速比随着节点数目的增大而增大:45负荷节点的潮流计算运算速度已提高到2倍,当负荷节点数目大于45时,还可获得2倍以上的加速比;但当矩阵规模小于20时,GPU方法实现时间大于CPU.这是由于计算量小、受显卡数据总线带宽所限.显存与内存数据通信所花时间较长,在整个程序运行完成总时间中占据了较大比重,无法发挥GPU高效并行计算的能力.
4.2 仿真信息可视化显示
以上海洋山港110kV供电系统中的23kV配电网作为仿真系统物理设备模型,线路阻抗和节点负荷功率取自文献[9]的表5a,b.
表3即是本方法与Goswami所提方法在文献[9]中所得节点电压的求解结果比较.两者的计算数值相近,说明本方法的正确性;在同样迭代求解3次的情况下,本方法收敛精度误差是0.9758×10-5p.u(标幺值),远远小于文献[9]方法的3.6716×10-5p.u.说明本方法的计算精度较高.图7a所示为面积为8.14km2洋山港配电系统3DGIS仿真整体绘制效果图;图7b为配电系统的地下电缆三维仿真绘制效果图;图7c为23kV配电网中监测第17母线的电力开关柜,电流仪表指针指示为34A,并附有该设备所处位置的经度、纬度地理信息和潮流计算所得的该母线的电流幅值和角度.图7d为23kV配电网中第7负荷点对应的变压器.此设备没有数值显示仪,本系统在设备旁以文字说明其位置地理信息和潮流计算所得的电压幅值、角度等仿真计算信息.4个图均为固定视点抓图,但在程序运行中可通过自主漫游方式或设定路线方式对潮流计算仿真信息进行可视化展示.本方法所绘制图像具有高度的真实感,人机交互方式灵活,能正确、生动、形象地反映仿真配电网设备三维空间位置关系及其运行状态.

表3 潮流计算结果Tab.3 Results of the power flow calcalation

5 结语
在回路阻抗法的基础上,针对配电系统,提出了一种快速潮流计算与仿真信息可视化方法.其创新性主要在于:十字链表用于配电网的网络拓扑结构存储,便于网络重构与构成弱环网的负荷节点的判定,与关联矩阵相结合,可完成对无环或有环配电网阻抗矩阵的自动生成,并可不受节点编号顺序限制计算各内节点电压、支路电流;基于CUDA编程模型提出了基于right-looking LU分解法的并行高斯消去算法,利用GPU对潮流计算快速求解;并将计算结果在3DGIS系统中进行仿真可视化.算例仿真实验证明,该方法对节点编号无特殊要求,求解计算快速、精确、稳定、交互性能好,能使调度人员、培训人员对各种节点类型参数设置的无环或有环配电网进行潮流计算和三维可视化仿真,从中直观、形象地认识到地理和设备之间的对应关联信息,理顺电力设备之间的运行逻辑关系,分析掌握配电网的现行运行状态,切实提高管理水平和学习效率,可广泛应用于配电网规划、分析、人员培训等领域.
今后,将基于该方法对配电网短路、三相潮流等特殊性质的潮流计算进行仿真模拟与可视化,同时结合高压输电网的潮流计算方法,求解大规模电力系统的潮流计算,充分发挥该算法并行计算的高效性.
[1]Godwin N.Application of modern load flow techniques to electric power systems[M].Saarbrucken:LAP LAMBERT Academic Publishing,2010.
[2]Teng J.A modified Gauss-Seidel algorithm of three-phase power flow analysis in distribution networks[J].International Journal of Electrical Power and Energy Systems,2002,24(2):97.
[3]Jegatheesan R,Nor N M,Romlie M F.Newton-Raphson power flow solution employing systematically constructed Jacobian matrix[C]//2008 IEEE2nd International Power and Energy Conference.Piscataway:IEEE,2008:180-185.
[4]Kulworawanichpong T.Simplified Newton Raphson power-flow solution method[J].International Journal of Electrical Power and Energy Systems,2010,32(6):551.
[5]Yang H,Wen F,Wang L,et al.Newton-Downhill algorithm for distribution power flow analysis[C]//2008 IEEE 2nd International Power and Energy Conference.Piscataway:IEEE,2008:16L28-1632.
[6]Aravindhababu P,Ashokkumar R.A fast decoupled power flow for distribution systems[J].Electric Power Components and Systems,2008,36(9):932.
[7]Chang G W,Chu S Y,Wang H L.An improved backward/forward sweep load flow algorithm for radial distribution systems[J].IEEE Transactions on Power Systems,2007,22(2):882.
[8]Eminoglu U,Hocaoglu M H.Distribution systems forward/backward sweep-based power flow algorithms:a review and comparison study [J]. Electric Power Components and Systems,2009,37(1):91.
[9]Goswami S K,Basu S K.Direct solution of distribution systems[J].IEE Proceedings C:Generation,Transmission and Distribution,1991,138(1):78.
[10]王守相,阮同军,刘玉田.配电网潮流计算的回路阻抗法[J].电力系统及其自动化学报.1998,10(1):12.WANG Shouxiang,RUAN Tongjun,LIU Yutian.Distribution system power flow based on loop-impedance equations[J].Proceedings of the International Conference on Energy Management and Power Delivery,1998,10(1):12.
[11]王丹,常宝立.一种用于配网潮流计算的节点编号新方法[J].电力系统及其自动化学报.2003,15(1):22.WANG Dan,CHANG Baoli.Distribution system power flow based on loop-impedance equations[J].Proceedings of the International Conference on Energy Management and Power Delivery,2003,15(1):22.
[12]刘耀年,岂小梅,李国鹏,等.基于回路阻抗法的配电网潮流计算[J].继电器,2004,32(8):8.LIU Yaonian,QI Xiaomei,LI Guopeng,et al.Load flow algorithm for distribution network based on loop-impedance method[J].Relay,2004,32(8):8.
[13]汪宇霆,张焰,张益波.基于改进回路电流法的配电网潮流通用算法[J].电力系统保护与控制.2010,38(20):57.WANG Yuting,ZHANG Yan,ZHANG Yibo.A general load flow method for distribution systems based on improved loop-current method[J].Power System Protection and Control,2010,38(20):57.
[14]Sun Y, Overbye T J. Visualizations for power system contingency analysis data[J].IEEE Transactions on Power Systems,2004,19(4):1859.
[15]Milano F.Three-dimensional visualization and animation for power systems analysis[J].Electric Power Systems Research,2009,79(12):1638.
[16]NVIDIA.NVIDIA CUDA programming guide 3.2[EB/OL](2010-10-22).http://developer.download.nvidia.com.
[17]Dongarra J J,Hammarling S,Walker D W.Key concepts for parallel out-of-core LU factorization [J]. Computers and Mathematics with Applications,1998,35(7):13.
[18]Tomov S,Dongarra J,Baboulin M.Towards dense linear algebra for hybrid GPU accelerated manycore systems[J].Parallel Computing,2010,36(5-6):232.
[19]Wakita A,Matsumoto F.Information visualization with Web 3D spatial visualization of human activity area and its condition[J].Computer Graphics(ACM),2003,37(3):29.
[20]Ltifi H,Ayed M B,Alimi A M,et al.Survey of information visualization techniques for exploitation in KDD[C]//7th IEEE/ACS International Conference on Computer Systems and Applications.Piscataway:IEEE,2009:218-225.
[21]Baran M E,Wu F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Transactions on Power Delivery,1989,4(2):1401.
