车用天然气储罐脱附放气过程热力特性
2012-10-30谭羽非牛传凯卜宪标
谭羽非,牛传凯,卜宪标,2
(1.哈尔滨工业大学 市政环境工程学院,黑龙江 哈尔滨 150090;2.中国科学院广州能源研究所,广东 广州 510640)
天然气作为清洁汽车燃料正在得到迅速发展.汽车用天然气主要有两种储存方式:压缩天然气储罐和吸附天然气储罐.压缩天然气储存技术比较成熟,但在储存和使用过程中往往由于工作压力过高,运行时存在危险性,同时加气站耗能大,储气设备和管道需较厚壁面[1];而吸附天然气储罐虽储存压力较低,但在车用天然气储罐放气过程中存在非常明显的热效应[2],其脱附速度影响汽车的行驶速度.
目前,对于天然气的吸附储存技术还处在研究阶段,其研究方向主要有两个方面:一方面是采用高效的吸附材料,主要吸附材料有高比表面积的活性炭纤维和炭纳米管等,研究取得了一定的进展[3-5];另一方面是吸附热效应对储罐的影响,在天然气的吸脱附过程中产生大量的吸附热,降低了吸附材料的吸脱附性能,从而降低天然气储罐的使用效率.一些学者对热效应对储罐的影响进行了研究[6-7],但对热效应在汽车行驶过程中产生的影响研究较少.
本文以车用天然气储罐为研究对象,基于脱附过程中天然气流动和换热的特点,依据流体力学、热力学、传热学的理论建立了脱附过程的数学模型,通过数值模拟求解,模拟计算了吸脱附过程中储罐内温度、压力和吸附量的变化,并且分析了影响脱附量的因素,为吸附天然气汽车在行驶过程中消除脱附热效应措施的提出,提供理论依据.
1 脱附过程中数学模型的建立
圆柱形车用天然气储罐内装有多孔介质活性炭纤维作为吸附剂,用来储存吸附相的天然气.假设:吸附剂及吸附相温度相同;忽略床层和罐壁的接触热阻;储罐内压力均匀,温度仅考虑径向分布.建立数学模型如下[8]:
(1)连续性方程
由于储罐内的气体是吸附相或气相,储罐脱附向外释放气体的过程就是罐内吸附相和气相质量随时间变化的过程.因此,连续性方程的表达式如下:

式中:εt为总孔隙率,εt=εb+εp(1-εb),εb为床层孔隙率,εp为活性炭颗粒孔隙率;ρg为气相气体密度,kg·m-3;ρb为活性炭密度,kg·m-3;q*为活性炭瞬时吸附量,kg·kg-1;m·为单位体积的放气速度,kg·m-3·s-1;t为时间,s.
(2)放气速度方程

式中:M 为车的用气速度,kg·s-1;L为储罐长度(内部空间长度),m;r为储罐内某点到轴心的距离,m;R0为储罐内半径,m.中的单位体积指的是储罐半径方向r和r+Δr之间所包含的圆环体积(长度为L)对半径积分,可得整个储罐的放气速度,也就是车的用气速度.
(3)能量方程
脱附过程是吸热过程,在能量方程中脱附吸热相当于内热源项.由于脱附过程比较慢,气体流速较低,所以对流项可以忽略.能量方程的表达式如下[9-10]:

式中:λe为床层有效导热系数,W·m-1·K-1;qst为吸附热,J·kg-1;T 为储罐内温度,K;Cpg为气体热容,J·kg-1·K-1;Cps为活性炭热容,J·kg-1·K-1;P 为储罐内压力,Pa;υ为粘度,m2·s-1.
(4)气体状态方程

式中:R为气体常数,J·kmol-1·K-1;Mg为天然气的摩尔质量,g·mol-1.
(5)吸附等温线方程
天然气在常温条件下脱附是超临界状态的脱附,而超临界气体的吸附为单分子层吸附,选用典型的Langmuir方程[11],能够很好地描述单分子层的吸附和脱附特性.

式中:qeq为活性炭平衡吸附量,kg·kg-1;qm为活性炭饱和(最大)吸附量,kg·kg-1.
(6)脱附速度的线性推动力方程

式中:k为吸附传质速度,s-1.
(7)初始条件和边界条件
储罐壁面处按第三类边界条件处理,储罐中心处的温度为轴对称,即第二类边界条件.

式中:PI为储罐内初始压力,Pa;TI为储罐内初始温度,K;Tw为储罐壁面温度,K;ρw为储罐壁密度,kg·m-3;Cpw为储罐壁热容,J·kg-1·K-1;λw为罐壁导热系数,W·m-1·K-1;ha为储罐外壁对流换热系数,W·m-2·K-1;Ta为储罐外空气温度,K;Bw为储罐壁厚,m.
2 方程的离散及模型的求解
将公式(1),(2)和(3)用控制容积积分法进行离散


离散后的方程用Newton-Raphson方法进行求解,其中,时间步长 Δt=0.01s,空间步长 Δr=0.01m.求解过程的流程如图1所示.

图1 计算流程图Fig.1 Flowchart of calculation
具体求解步骤如下:
令Pda=PI,Pxiao=101325Pa,给定车的用气速度M*.
(1)计算压力P0和脱附量.取P0=(Pda+Pxiao)/2,根据公式(5)和(6),计算压力为P0工况下的脱附量.
(2)计算温度场.根据步骤(1)计算的压力和脱附量,按公式(3)和(4)计算温度场.
(3)计算用气速度M.用公式(1)和(2)计算M,如果脱附量满足M*,直接跳到步骤(4).如果脱附量不满足,则按Newton-Raphson方法计算压力.
具体方法为:若上一步计算出的脱附量大于M*,取Pxiao=P0;若上一步计算出的脱附量小于M*,取Pda=P0,返回步骤(1)开始计算,直到脱附量满足M*.
(4)判断压力P0的大小,若P0>PT,返回步骤(1)进行下一时刻的计算;若P0<PT,结束计算.
PT表示脱附终了的压力,在本文中,PT=0.16MPa,若储罐内压力低于PT,则储罐内气体的脱附速度就不能满足车在高速时的能量需求.
3 模拟算例
车用天然气汽车储罐内部空间长L=1.0m,半径R0=0.15m,内装满多孔介质活性炭,见图2.储罐脱附压力从3.50MPa开始到0.16MPa结束.以上海帕萨特轿车为例,该车100km耗汽油量为8L,在时速为100km时,按燃料燃烧放出相同的热量计算,天然气的脱附速度为1.315g·s-1,计算中用到的其他物性参数和相关参数如表1所示.

图2 储罐示意图Fig.2 Schematic diagram of tank

表1 计算中用到的参数数值Tab.1 Parameter value used in calculation
3.1 储罐温度场分析
车速100km·h-1、脱附速度为1.315g·s-1时,计算得脱附时间为2080.1s.由于脱附过程中吸热,造成吸附剂平均温度从293.15K降低到250.46 K,脱附终了时的天然气脱附质量2.735kg,脱附效率为75.51%.
脱附终了时储罐的径向温度见图3所示,吸附剂温度最低点发生在吸附剂的内部,即储罐的中心,温度降到了244K,而靠近壁面的温度降低到272 K,明显高于中心的温度.因此,在脱附放气的过程中,改变吸附剂内部的温度,将更有利于脱附.
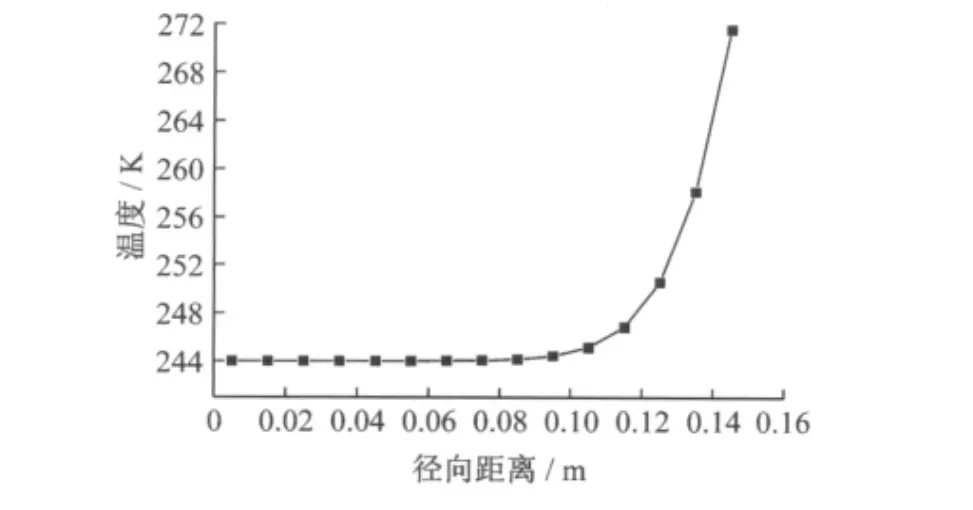
图3 脱附终了时储罐的径向温度Fig.3 Radial temperature of storage tank at the end of discharge
图4所示为壁面温度随时间的变化,从脱附初期的293.15K降到脱附终了的282K.由图可知,在脱附过程的前5min,壁温由293.15K降到292.75K,降幅仅为0.45K.说明脱附前期,温度变化较慢,而在脱附后期,温度变化反而较快.从30~35min之间,壁温由284K降到282K,降幅为2K.对于这种变化趋势,图6可以给出很好的解释:在脱附后期,吸附相的释放量变大,所需的热量变大,所以罐壁温度下降速度变快.
由以上分析可知,在脱附的过程中,吸附剂的温降很大,对脱附效率的影响很大.因此,在脱附过程中,向储罐内供热能够增大脱附效率.

图4 壁面温度随时间的变化Fig.4 Temperature variation of wall with time
3.2 储罐压力变化分析
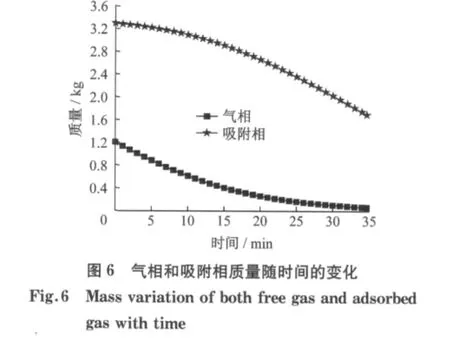
在脱附的过程中,不仅储罐内的温度在变化,储罐内的压力也在变化,变化规律如图5所示.同时,储罐中的天然气以两种形式存在,分别为气相和吸附相.而在脱附的过程中,它们的存在形式也发生着变化,变化规律如图6所示.

由图5可知,脱附过程的压力由初期的3.5MPa降到脱附终了的0.16MPa.在脱附开始阶段,压力下降得较快,在脱附过程的前10min,压力由3.5MPa降到了1.76MPa,降低了1.74MPa.随着脱附时间的增加,虽然吸附剂的温度已经降低了很多,但是压降却变慢.在脱附的最后10min,压力从0.48MPa降到0.16MPa,只降低了0.32MPa.这是由于在开始阶段,储罐释放的主要是气相状态的天然气,压力下降快,随着时间的延续,释放的吸附相的天然气变多,压力下降变慢.这也说明了活性炭在低压的情况下具有较好的吸脱附特性.
图6是气相和吸附相质量随时间的变化曲线.在脱附开始时,气相变化较快,而吸附相变化较慢,这说明供气阶段的前期,气相气体的释放速度较快.而在脱附的后期,由于压力降低,气相气体减少,说明此时主要是靠释放吸附相的气体供给汽车所需的燃料.这也说明了活性炭吸附剂具有较好的低压脱附特性.图6可以对图4的温度特性给出很好的解释:在脱附开始时主要是释放气相的气体供给汽车使用,所以吸附热很小,吸附剂的温降缓慢,而在后半段主要是释放吸附相的气体,吸附热增加,所以温降变快.
由以上分析得出结论:脱附过程吸热,系统温度降低,导致储罐脱附效率下降.所以,为了增强脱附效率,应在脱附过程中向储罐供热,来降低或者消除热效应的影响.
3.3 脱附速度的影响
天然气储罐的脱附速度是由汽车的行驶速度决定的,如车速30km·h-1时的脱附速度为0.395g·s-1,车速60km·h-1时的脱附速度为0.789g·s-1.由表2可知,不同的脱附速度所对应的脱附质量不同,脱附过程持续的时间也不同,脱附速度越小,脱附质量越大,该脱附过程所持续的时间也越长.
在整个脱附过程中,脱附需要的热量等于吸附剂、壁面、气体得失热量和膨胀做功的和,写成等式为

式中:Qall为脱附过程中储罐吸收的总热量,kJ;Qad为吸附剂的热量,kJ;Qw为储罐壁面吸收的热量,kJ;Qg为储罐内气体吸收的热量,kJ;Qnc为储罐通过自然对流吸收的热量,kJ;QW为吸附过程中气体膨胀对外的做功量,kJ.
以脱附速度1.315g·s-1为例,在脱附终了时,Qall=1795.7kJ,Qad= 1249.4kJ,Qnc=28kJ,Qw=428.6kJ,QW=174.71kJ,Qg=264.41kJ.从上面的计算可知,自然对流提供的热量很少,而壁面提供了脱附所需热量的23.87%.
表2表明,脱附效率随着脱附速度的增加而降低,这是因为脱附过程吸热,脱附速度越大,在相同的时间内吸收的热量越多,吸附剂的温降就越大,而低温不利于吸附剂的脱附.在脱附速度分别为0.395g·s-1,0.789g·s-1,1.052g·s-1,1.315 g·s-1和1.578g·s-1时,壁面所提供的热量分别占脱附吸热量的30.82%,27.48%,25.52%,23.87%和22.47%,即壁面所提供的热量随脱附速度的增加而减小.这是因为随着脱附速度的增加,脱附系统的温降变快,而壁面无法在短时间内提供内部所需的热量.以脱附速度1.315g·s-1为例,在脱附终了时刻,罐壁面的温度为281.91K,而吸附剂平均温度为250.46K.

表2 不同脱附速度下的脱附过程比较Tab.2 Comparison of desorption processes at different discharge rates
从以上分析可知,储罐壁面由于热容量较大,对脱附效率有很大影响.因此,要改变系统的脱附效率,可以从改变储罐壁面的传热特性和热容量入手.
本文的计算结果表明,储罐压力从3.5MPa降至0.16MPa,脱 附 速 度 为 110.46L·min-1(1.315g·s-1)时,脱附效率为75.51%,储罐中心的温降达49℃左右.Chang和Talu[12]的实验结果表明在非绝热快速脱附的条件下(脱附速度15.0L·min-1,环境温度为18~22℃),储罐中心的温降可达37℃,脱附效率比等温条件下损失25%.本文计算的中心的温降比Chang和Talu的实验结果低,原因是本文的储罐是面向车用的,脱附速度较大,所以温降较大.
4 结论
本文主要讨论了车用吸附天然气储罐脱附过程中储罐壁温、罐内压力、吸附剂温度以及脱附量和脱附效率等参数的变化情况,并得到以下几点结论:
(1)脱附过程是吸热过程,吸附剂温度的降低对脱附质量有很大影响.脱附过程中吸热,造成吸附剂平均温度从293.15K降低到250.46K,脱附效率比等温脱附减少24.49%.
(2)脱附过程中,储罐中心温度最低.中心温度为244K,降低了49K.
(3)脱附速度越大,脱附效率越低.脱附速度由0.395g·s-1增加到1.578g·s-1时,脱附效率由78.80%降到75.11%.
(4)储罐壁面热容量对脱附效率有很大影响.在不同的脱附速度下,壁面所提供的热量占脱附吸热量的22.47%~30.82%不等,脱附速度越大,壁面提供的热量越少.
(5)储罐壁面和吸附剂之间以及吸附剂内部存在很大的温度梯度.
[1]欧成华,李朝纯,杜建芬,等.吸附天然气汽车技术研究与对策[J].天然气工业,2002,22(2):90.OU Chenghua,LI Chaochun,DU Jianfen,et al.Research and countermeasures of adsorbed natural gas vehicle technology[J].Natural Gas Industry,2002,22(2):90.
[2]钱焕群,陈宝明,张建,等.天然气吸附床脱附过程的传热实验研究[J].山东建筑大学学报,2008,23(5):394.QIAN Huanqun,CHEN Baoming, ZHANG Jian, et al.Experimental study of heat transfer in natural gas adsorption bed during a desorption process[J].Journal of Shandong Jianzhu University,2008,23(5):394.
[3]Najibi H,Chapoy A,Tohidi B.Methane/natural gas storage and delivered capacity for activated carbons in dry and wet conditions[J].Fuel,2008,87(1):7.
[4]刘保华,赵乃勤,李家俊,等.用活性炭纤维吸附天然气的研究[J].中山大学学报:自然科学版,2003,42(增):126.LIU Baohua,ZHAO Naiqin,LI Jiajun,et al.Research of ACFs absorbing natural gas[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2003,42(suppl.):126.
[5]Zhang T,Walawender W P,Fan L T.Grain-based activated carbons for natural gas storage[J].Bioresource Technology,2010,101(6):1983.
[6]王皆腾,孙俊芳,刘中良.天然气吸附储存容器的结构优化分析[J].工程热物理学报,2009,30(10):1729.WANG Jieteng,SUN Junfang,LIU Zhongliang. Optimal analysis of an adsorbed bed in an adsorbed natural gas storagesystem[J].Journal of Engineering Thermophysics,2009,30(10):1729.
[7]孙俊芳,刘中良,蒋文明,等.天然气吸附储存过程的数值模拟研究[J].热科学与技术,2009,8(3):231.SUN Junfang,LIU Zhongliang,JIANG Wenming,et al.Numerical study of charging process of adsorbed natural gas storage[J].Journal of Thermal Science and Technology,2009,8(3):231.
[8]卜宪标.车用天然气吸附储存及热效应模拟研究[D].哈尔滨:哈尔滨工业大学市政环境工程学院,2008.BU Xianbiao.Simulation research on adsorption and adsorptive thermal effects of natural gas for vehicles[D].Harbin:Harbin Institute of Technology.College of Municipal &Environment Engineering,2008.
[9]Gadalla M A.Simulation of intermittent thermal compression processes using adsorption technology [J].Journal of the Franklin Institute,2007,344(5):725.
[10]Wojcik A M W, Jansen J C, Maschmeyer Th.Thermodynamically consistent thermal energy equation for an adsorbent/fluid system [J].International Journal of Heat and Mass Transfer,2001,44(12):2379.
[11]Tseng R,Wu F.Analyzing concurrent multi-stage adsorption process of activated carbon with a favorable parameter of Langmuir equation [J].Journal of the Taiwan Institute of Chemical Engineers,2009,40(2):197.
[12]Chang K J, Talu Orhan. Behavior and performance of adsorptive natural gas storage cylinders during discharge[J].Applied Thermal Engineering,1996,16(5):359.
