基于仿生学的区域交通自适应网络生长模型
2012-10-30卢丹妮
田 园,李 晔,卢丹妮
(同济大学 交通运输工程学院,上海 201804)
区域发展是当下世界性的潮流,交通系统在促进区域协调发展与增强区域竞争力中处于基础与引导地位.目前,区域交通网络规划的理论和技术多是参照城市交通或单一交通方式特别是公路网规划的理论和方法,其核心是“供需平衡”导向的四步骤模型.由于四步骤模型的运行机理是经济决定交通的单向机理,因而不能反映交通条件改善对区域经济发展的反馈作用,故在模型机理中无法体现诱增交通需求对基础设施供给的影响,从而导致依据四步骤模型预测和设计得到的运输网络或通道在运行一段时间后交通拥挤严重,区域交易成本居高不下.
针对上述问题,笔者提出一个基于仿生学的区域交通自适应网络演化模型.该模型的灵感来源于生物学中的黏液菌觅食机理:黏液菌在觅食过程中,其原生质流与管道的正向反馈机制——“黏液菌中高流量的原生质会刺激管道的半径增加,而低流量的管道则会逐渐消失”.若把食物资源比作区域的主要城市,黏液菌的觅食管道比作区域交通网络,管道中的原生质流比作交通流量,则黏液菌所表现出来的这种特性与区域交通与经济互动反馈作用机理非常接近.将黏液菌的自适应觅食机理引入区域交通经济作用机理,将经济、人文、交通、地理等区域要素视为黏液菌觅食过程中的“食物”与外部环境,通过模拟黏液菌管道厚度随流量增大而增加这一黏液菌“生物智能”在时间上的演化,模拟区域交通网络与区域经济发展的反馈作用.这种基于仿生学的区域交通自适应网络生长模型,可应用于区域交通网络的布局规划中,并解决了传统模型无法考虑的诱增交通所造成的通道“供不应求”的情况.
1 文献综述
自1736年欧拉提出经典的“康尼斯堡七桥”问题,第一次引入交通网络的概念以来,各领域的专家和学者开始源源不断地探索交通网络及其时空演变特征.近代关于交通网络生长的研究起源于国外上世纪60年代到80年代的经济地理和区域科学运动时期,地理学家根据交通网络的结构演化与拓扑变化模拟交通网络的增长,其核心是用图论的方法及其元素来描述交通网络.Lachene[1]基于一个假设各向同性的交通网络,开发了一个阶段模型:初始网络被假设为没有路面铺装的道路网络,且经济活动均匀分布.随着城镇在某些线路的交叉处形成,连接各城镇的路网相应出现.当经济活动向城市中心集中时,一些常用道路变成铺装的道路,而乡村一些较少使用的道路则被废弃,最后出现一个将城市中心连接起来的高等级交通网络(可能是铁路网或高速公路网).区别于连接节点成网,Kolars和 Malin[2]用人口可达性平面模拟了土耳其铁路网的发展,认为交通连接出现在人口可达性平面的主要山岭线上.在Black[3]的研究中,缅因州的铁路网络起始于波特兰的一个树状分支,通过连接外围节点向外生长;建设连接节点之间线路的概率由考虑潜在收入、建设成本并用线路角度作为约束的函数决定;某一时间内某对节点间是否连接取决于函数值是否超阈值.
近年来,用户均衡算法被广泛地应用于解决网络设计问题(NDP).通常,NDP由双层框架构成[4-5]:下层表示给定投资下的需求行为均衡,上层表示交通规划者基于来自下层的唯一均衡流模式.为了实现社会福利最大化的投资决策,以连续的NDP处理现有路段通行能力扩大优化的问题,而离散NDP通过改变网络的实际拓扑,即通过增加或删除路段,优化交通供给.随着可获得的数据愈加充足、数据处理能力的提升,利用基于历史数据和统计分析的交通网络生长的经验模型研究逐渐成为研究热点.Levinson和 Karamalaputi[6-7]分别检验了网络条件、交通需求、人口特征、项目成本、资金约束与网络新建和扩建的关系,利用二项logit和混合logit模型,将每条路段的新建和扩建和历史数据建立联系.历史数据包括网络属性、扩建与建设历史,以及每条路段的年平均日交通量.
本世纪初,随着 Barabási[8]的著作《纽带:新网络科学》问世,复杂网络科学诞生,并逐步应用于交通网络生长研究中:复杂网络中节点连接的“偏好依附性”可以解释节点辐射网络的出现,如航空网络.当独立的节点连接到网络上时,它们倾向于连接到网络中已存在的较为重要的节点;尽管对于交通网络而言,节点的重要性并不像无标度网络一样与节点度有关,但直接连接可以降低成本,避免冗余路径之间的竞争.Xie和Levinson[9]基于设定的“最弱路段”,开发了一个网络生成的演化模型.该模型合并个体路段作为自治体,网络中最弱的路段可在迭代过程中被检验出.随后,该模型用于检验交通网络的拓扑变化,仿真对象为一个不发达地区内所有点与点之间的路径.随着网络演化,常用的路径得以加强,而较少用的路段被废弃,因此,通过一个自上而下的过程实现了网络的拓扑变化.“最弱路段”启发源于“贪婪算法”,其原理是通过在每个离散阶段实现局部最优,最终实现整体最优.
综上所述,目前交通网络生长的研究主要集中在交通地理、交通网络设计与优化、交通网络生长的经验模型以及复杂网络理论等四个领域,其研究目的主要是为交通网络设计与网络性质分析提供工具或理论支撑.笔者基于仿生学对交通网络生长建模,建立模拟区域交通网络与经济动态作用关系的区域交通经济自适应生长网络模型,是区域交通网络布局规划及交通网络设计研究的一个新视角,也是一次全新的尝试.
2 模型及原理
2.1 黏液菌觅食机理
黏液菌(Physarum)是一种多细胞核的单细胞有机体,是介于动植物之间的一种微生物,具有管状的网络结构及向食物聚集的特性,并通过这种构造获取外界营养和感知信息.如食物处于分散状态,黏流菌就会在食物之间形成管道,通过管道输送养分.Teroa等人的研究[10]发现,在黏液菌觅食过程中,初始阶段黏液菌只在相当近的范围觅食,最后扩大到自身能拓展到的最大范围.如图1所示.研究进一步发现,虽然黏流菌每次形成的网络不相同,但这些网络有着共同特点:经常用的管道会越来越发达,而不用的管道则会逐渐消失;最终使网络的总长度尽可能短,并确保在某处中断时有其他路径可绕行.这项研究为笔者通过模拟黏液菌觅食机理进而仿真区域交通网络生长,提供了灵感与启发.
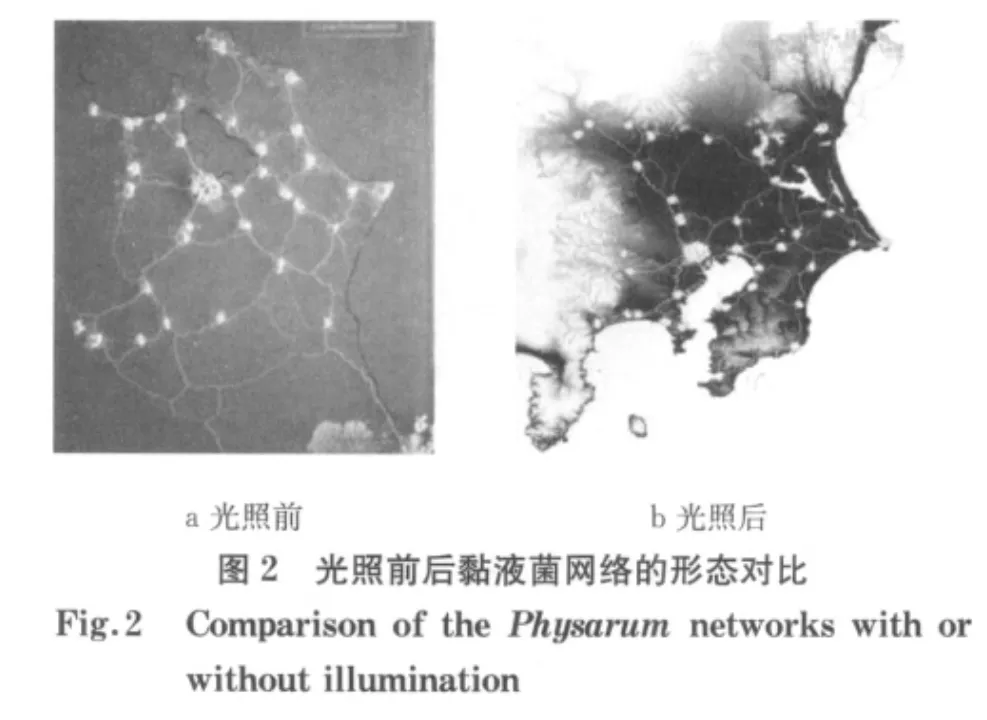
Teroa等人还利用黏液菌不喜光的特性,用光照射模拟地形地貌特征对黏液菌觅食管道网络的影响.图2为光照前后的黏液菌网络的变化.图2a说明,在没有照明时,黏液菌网络可不受约束地蔓延到任何食物;当光照于黏液菌的觅食网络时,网络发生变化,其觅食管道多产生于图2b中的深色部分.黏液菌的这种特性可用来模拟现实网络建设中的施工困难区域.该特性进一步表明,基于黏液菌觅食机理描绘区域交通网络是模拟区域交通网络生长的有效方法.

2.2 区域交通自适应网络生长模型
黏液菌觅食的主要机理就在觅食过程中,其管道中的原生质流构成了一个反馈回路——高流量的原生质会刺激管道的半径增加,而低流量的管道则会逐渐消失.黏液菌的初始状态由具有正方形的规则网格表示,并假设其已完全覆盖食物节点(黏液菌从某一点生长连接食物与黏液菌连接所有食物后的生长行为相同)[10].为了模拟上述过程,基于黏液菌觅食的区域交通自适应网络生长模型由以下几部分模型来描述:网络描述模型、流量表达模型、网络流的运动规则、以及网络随时间演化的自适应模型.
2.2.1 网络模型
根据Teroa等人的研究成果[11],黏液菌网络可用图论的方法表示.边表示黏液菌的管道,节点表示管道之间的相交连接或食物所在点(见图3),N1,N2分别表示食物节点;Ni,Nj表示非食物节点;Mij表示Ni与Nj之间的边,若同一对节点之间有若干条边,则分别表示为 M1,ij,M2,ij等.当2个节点之间没连通条件时,则节点之间无直接路径,如N3与N4.
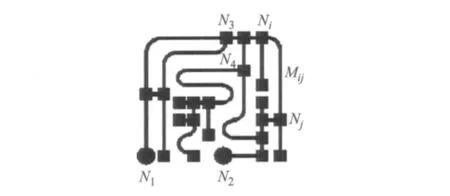
图3 区域交通自适应网络的拓扑抽象图Fig.3 A graphical representation of regional adaptive transport network
2.2.2 流量模型
设节点i与j处的压力分别为pi和pj,节点之间用长度为Lij、半径为aij的圆柱形管道连接,并假设管道中的流体为哈根-泊肃叶(Hagen-Poiseuille)流,则通过Mij的流量Qij可以表达为
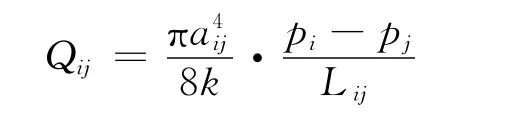
式中:Lij为表示i,j之间的管道长度;aij为管道Mij的半径;k为管道中流体的黏滞系数.
令Mij的传导系数Dij=/8k,则上式可进一步表示为

2.2.3 网络流运动规则
为了使网络中的流体“流动”起来,可在每个模拟时间段,选择一个食物节点作为驱动网络中流体流动的“起点”(N1),从该点流出的流量 ∑jQ1j=I0;另一个食物节点作为决定流体流向的“汇点”(N2),流入该点的流量 ∑jQ2j=-I0.式中,I0为流出起点(或流入汇点)的流量.为了维持网络流体“持续”流动,则需要制定一定的规则,决定哪些食物节点作为“起点”或“汇点”.为确保模型更具一般性,在选择起点时,节点的选择不是确定的,而是随机(简单随机)的.当起点选好决定“汇点”时,选择规则不是简单随机,而是具有某一概率分布的随机选择.
根据经济地理学中的潜能理论,不同城市之间的相互作用与各城市的规模成正比,与城市间的空间阻抗成反比.也就是说,在一个由城市构成的系统中,不同城市间的相互作用是概率的,这个概率是由城市的规模及其所处的区位所产生的.在潜能理论中,潜能表示一物体对另一个物体产生的能,如城市j对城市i所产生的能量是Mj/dij.其中,Mj是与城市质量(或规模)相关的变量,用节点城市i的人口规模表示;dij是与空间阻抗相关的变量,用节点i,j之间的管道最短距离表示.如果在一个城市系统中有n个城市,则对于城市i,总的潜能为

据此,在一个城市系统中,城市i与j联系的概率可表示为

上述概率就是在确定某起点后,该点在一次模拟过程中选择向某汇点流动的概率.
除了起点与汇点的选择原则外,在每个中间节点Ni(i≠1,2)处,流入节点与流出节点流量满足基尔霍夫定律,即流入流量与流出流量守恒:
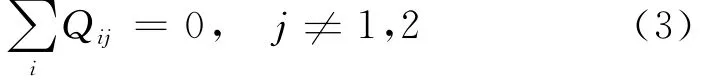
而对于起点N1与汇点N2,可分别用下列两个等式描述:

式(3)称为构建仿生自适应区域交通网络的局部守恒原则,式(4)称为仿生自适应区域交通网络的全局守恒原则.
2.2.4 自适应模型
式(1)~(4)表明,给定管道的初始传导性,并选定起点与汇点后,则通过黏液菌网络中各管道的流量可以计算出来.Tero等[11]的实验表明,在黏液菌觅食过程中,觅食管道的半径会随着流量的增加而增大.为了描述这种管道半径的自适应变化,可设传导系数Dij,根据流量Qij随时间变化,并利用下式来描述Dij随时间演化的情形Dij(t):

式中:r是管道的衰变率,f(·)是一个连续单调递增函数,且满足f(0)=0.假设函数形式为f(|Q|)=|Q|γ/(1+|Q|γ),即为一个S型曲线函数,如图4所示.γ是控制非线性反馈的参数(γ>0),黏液菌网络的自适应演化行为与函数形式f(Q)以及相应的参数值密切相关.
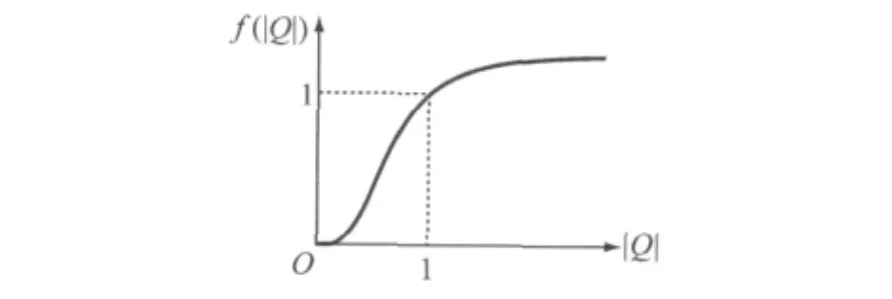
图4 自适应函数f(·)的曲线形式Fig.4 Illustration of the graph of function f (·)
仿生自适应区域交通网络模型的生长过程(自适应演化过程),就是Dij根据式(5)进行的过程.Pi和Qij等可通过求解各时刻具有Dij以及Lij特征值的网络局部与全局均衡方程(3)与(4)获得.在求解过程中,网络均衡方程会产生一个线性方程的稀疏对称矩阵,该矩阵可通过标准不完全乔莱斯基共轭梯度(ICCG)模型求解.由于在黏液菌网络的生长过程中,I0是一个不变的常数,因此,网络中边与边的关系实际上是流量竞争的关系.管道的传导性与管道的半径成正相关关系,因此,管道的消失可视为网络中该边的传导性降为零.在模型的自适应演化过程中,一些边(管道)生长或保留下来,而另一些边则萎缩直至消失.当剩下的边构成一个连接各食物节点的路径集合时,则认为模型的自适应网络生长完成.
3 区域交通自适应网络生长仿真实验
区域运输通道是城市群城际交通的骨干网络,也是城际间出行优先选择或大概率选择的交通路径,对于保障区域各城市间快捷高效的联系具有重要意义.本节以长三角地区16个城市为例,利用前述的区域交通自适应网络生长模型模拟长三角区域运输的形成与演化.用形状均匀的网格表示黏液菌网络,Lij为1或1.414,Dij的初始值可随机设置.现令全部Dij初始值为1,表示覆盖长三角地区的黏液菌网络各管道具有相同的半径.当I0=300,γ=2时,仿真得到的长三角区域自适应运输通道网络如图5所示.图中的右列为由matlab软件表示的仿真图,左列为基于matlab输出数据的ArcGIS仿真图.
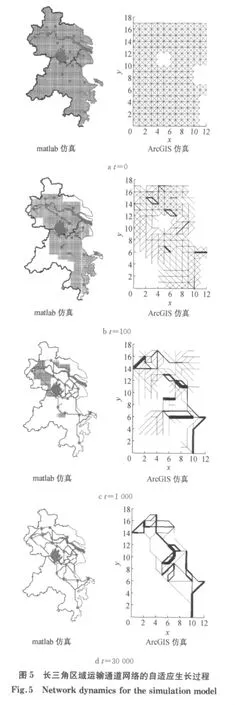
t=0时(如图5a),表示黏液菌与食物节点的初始状态,此时黏液菌布满整个长三角地区.文中用形状均匀的网格表示.网格的边表示里面具有原生质流的黏液菌管道,16个食物节点(对应于16个城市)在各管道的交叉处.当t=100时(图5b),相邻食物节点之间的黏液菌管道由于流量增加而变粗,远离食物资源的管道网络迅速退化并消失.也就是说,传导系数Dij较低的管道中的流量逐渐降低并趋近于零(其所对应的边消失),而传导系数较高的边则被保留下来并变粗.当t=1000(图5c)时,所有食物节点已由演化过的黏液菌管道所连通,但部分食物节点周围存在一定数量“死胡同”管道.当t=30000(图5d)时,黏液菌网络生长已趋于稳定,长三角区域自适应运输通道构建完成.
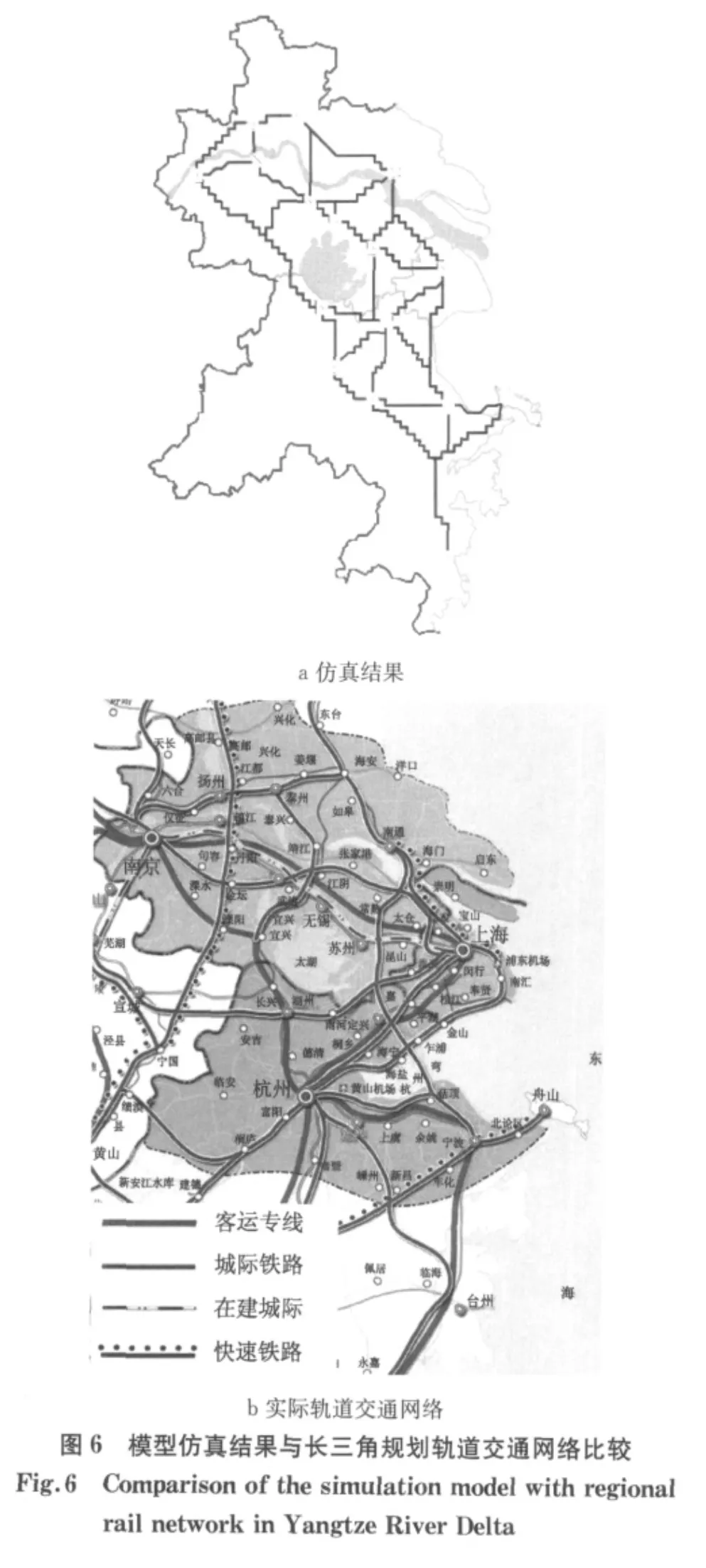
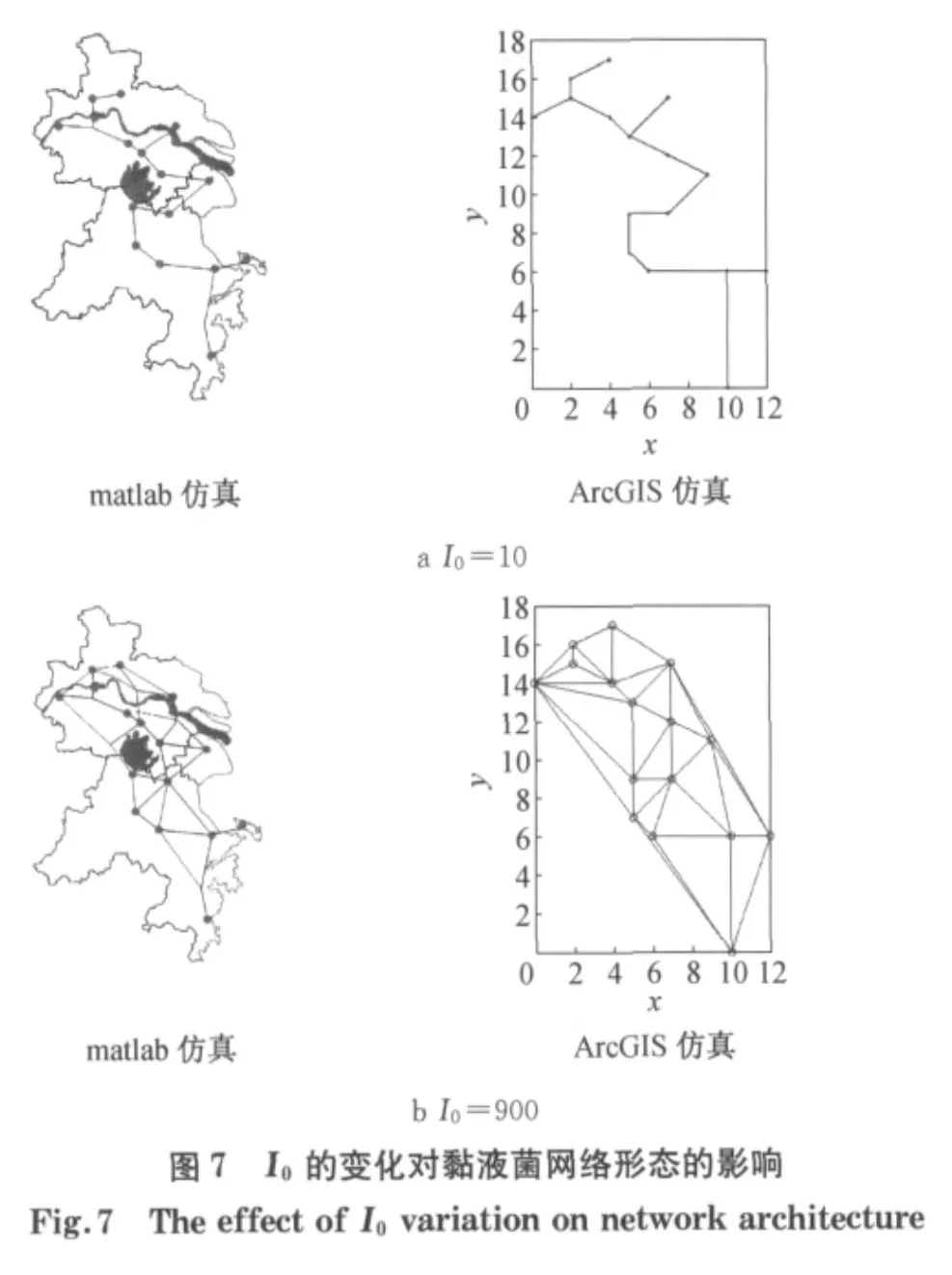
此外,区域运输网络的形态会随着I0的改变而变化,当I0=300时,所生成长三角区域运输通道与长三角的城际轨道交通网络基本一致,如图6所示.总体上,减少I0会使得网络向着最小生成树的方向发展,I0=10时所生成的长三角区域交通网络如图7a所示,这时,网络的总长度最小,各城市之间的平均距离最大;相反,增加I0促进了城市间可选择线路的生长,当I0=900时,得到的网络有类似于Delaunay三角的形态(图7b).长三角地区交通自适应网络随时间变化,以及随着区域交通活动总量变化而改变的仿真结果表明:① 基于黏液菌觅食机理的区域交通自适应网络模型,可以较好地模拟区域交通网络结构随着区域交通活动规模增大而日趋复杂的发展趋势,与实际情况吻合;② 随着模型参数值的改变,模型表现出自适应的特征:随着时间的变化,联系各城市间的交通路径从“聚能点”出发,并逐渐出现在“高势带”,最终形成区域运输通道.
4 结语
交通系统在促进区域协调发展与增强区域竞争力中处于基础与引导地位,如何构建高效率的区域交通网络,特别是区域运输通道,是促进区域社会经济一体化发展、提供城市间高品质交通服务的重要课题.受黏液菌觅食机理启发,构建了区域交通自适应网络的生长模型,包括网络描述模型、流量表达模型、网络流的运动规则,以及网络随时间演化的自适应模型等4个部分;并通过自身规则迭代,动态地构建与区域社会经济协调发展的自适应交通网络:随着模型仿真时间的推移,流量大的网络路径(通道),流量进一步增加并保留下来;而流量小的路径则流量逐渐减小并最终消失,从而得到区域交通的自适应网络(或通道).此外,通过调整模型中的一系列参数,还可构建不同特征的网络方案,如总长度最小的生成树网络、鲁棒性更强的达劳内三角网络等.该模型可反映区域交通网络与经济的自适应反馈作用机制,从而弥补了传统模型经济决定交通单向机理、交通无法反向作用于经济的缺陷,为区域交通发展战略在通道布局规划及遴选上提供了定量分析的工具.
[1]Lachene R.Networks and the location of economic activities[J].Regional Science Association,1965,14:183.
[2]Kolars J F.Malin H J.Population and accessibility:an analysis of Turkish rail roads[J].The Geographical Review,1970,60:229.
[3]Black W.An iterative model for generating transportation networks[J].Geographical Analysis,1971(3):283.
[4]LeBlanc L J.An algorithm for the discrete network design problem [J].Transportation Science,1975,9(3):183.
[5]Yang H,Bell M G H.Models and algorithms for road network design:a review and some new developments [J].Transportation Review,1998,18:257.
[6]Levinson D,Karamalaputi R.Induced supply:a model of highway network expansion at the microscopic level [J].Journal of Transport Economics and Policy,2003,37:297.
[7]Levinson D,Karamalaputi R.Predicting the construction of new highway links [J].The Journal of Transportation and Statistics,2003(6):81.
[8]Barabási A.Linked:the new science of networks [M].Jackson:Perseus Publication,2002.
[9]Xie F,Levinson D.Modeling the growth of transportation networks:a comprehensive review [J].Networks and Spatial Economics,2007,9(3):291.
[10]Teroa A,Kobayashi R,Nakagaki T.A mathematical model for adaptive transport network in path finding by true slime mold[J].Journal of Theoretical Biology,2007,244:553.
[11]Tero A,Takagi S,Saigusa T,et al.Rules for biologically inspired adaptive network growth [J].Science,2010,327:439.
