高速公路网络交通突发事件辐射范围预测模型
2012-10-30丛浩哲王俊骅童世鑫
丛浩哲,王俊骅,童世鑫
(1.同济大学 道路安全与环境教育部工程研究中心,上海 201804;2.公安部道路交通安全研究中心,北京 100062;3.林同棪国际工程咨询(中国)有限公司,重庆 401121)
高速公路作为承载快速运动和大流量交通流的道路载体,其安全和畅通一直是国家主干公路网交通管理中的两大重心,而交通突发事件情况下的应急处置管理,则是非常态交通管理的核心.交通突发事件辐射范围的预测是事件时空态势预测的重要内容,也是交通事件管理系统中的重要决策依据,是实现先进的突发交通事件管理和驾驶员信息服务的基础.研究交通突发事件辐射范围对于事件现场状况和未来走势的理解和预测、应急资源需求和资源调度、应急预案生成和交通组织管理决策优化等方面,具有重要的理论意义和实际应用价值.
国外对于预测高速公路交通事件所造成的排队长度的研究已有几十年的历史.1973年,Chow综合了冲击波理论和排队论,描述了事件发生时路段排队长度的变化趋势[1],Messer等人将波动理论应用于发生异常交通事件的高速公路上,预测旅行时间[2].1985年,Kaufmann选择了美国某高速公路上的交通事件,来验证考虑了排队长度和延误模糊预测模型,绘制了流量模糊度与排队长度和延误预测的关系图[3].1986年,Morales提出了利用到达离去曲线估计排队长度和延误,假设到达率和离去率是不变的确切值[4].1995年,AI-Deek等人提出了基于冲击波理论的宏观方法,对单起事件和多起事件的延误预测进行了探讨[5].2001年,Sheu提出了随机排队预测模型,基于车道变换行为定义了6个随机交通状态参数,以反映事件发生点的排队长度[6].车辆排队的研究主要是结合有信号灯的交叉口通行能力计算来进行,Lawson等通过累计频率曲线研究瓶颈路段排队长度[7].
国内,姚荣涵和王殿海采用交通流理论中的二流理论和微积分方法,讨论了拥挤交通流当量排队长度的变化率模型,并利用VISSIM模拟数据验证模型[8].臧华和彭国雄分析了高速道路交通事故发生后交通流的变化情况,并采用车流波动理论推导出排队长度随时间变化的公式[9].王建军在封闭路段集散波模型的基础上,讨论了分流措施产生的干预波对原有集散波传播的影响,为包括出口匝道的路段集散波传播研究提供了借鉴的模型[10].郑黎黎等建立了交通事件排队长度模糊预测模型和延误模糊预测模型,分析了事件发生期间交通流量和通行能力及事件待续时间的模糊度变化对排队长度和延误预测结果的影响[11].
事件辐射范围实质就是拥堵扩散的范围.综合国内外研究现状可知,常用的估算拥堵队列长度的理论方法主要有排队论和集散波理论,且多数研究局限于单一道路的建模分析.在路网环境中,交通事件影响范围已不单单局限于事发路段,其影响将通过匝道扩散到衔接道路上;另一方面,交通事件并不一定会使上游车流完全堵塞,随着干预措施的实施,事件断面的通行能力可能发生变化,因而事件对上游交通的影响力也会随之改变.这是排队论难以解决的问题.然而,集散波模型可以从更加宏观的角度,将交通流的基本参数作为变量来描述交通状态的传播.当交通事件断面通行能力改变时,只需将新的集散波加入原有模型中,而不必修改整个模型.因此,集散波理论具有更强的适应能力.然而,目前大多数集散波传播模型仅仅针对事发路段,所得到的结果也只是在单一线性维度上的排队长度的预测.在路网日渐密集的今天,交通事件对交通流的影响不再局限于单一道路.要分析交通事件对整个路网的影响,首先需要考虑出入口匝道情况下的集散波传播模型.
1 传统车流集散波传播模型分析
本文研究的高速公路交通突发事件属狭义的交通事件范畴,是指偶然发生的交通事件并影响交通流的正常运行,如车辆碰撞、刮擦、抛锚、炸胎、着火、物品散落、行人穿越等,主要包括交通事故和清障类事件.交通事件发生后,分析上游交通流特征及路段通行能力有助于了解事件对路段交通流的阶段性影响过程及其程度.对事件条件下传统车流集散波传播模型的分析,有助于对车流波动理论和线性交通流理论的理解,并为考虑出入口匝道及衔接道路的路网事件辐射范围预测模型的建立提供理论基础.
1.1 事件上游交通流特征及通行能力变化分析
美国《道路通行能力手册》将交通事件持续时间分为4个阶段:事件检测及确认时间、事件响应时间、事件清理时间和交通恢复时间.随着事件检测技术的日趋成熟和广泛应用,交通事件检测及确认的时间也越来越短,便于研究,将事件检测及确认时间和事件响应时间合并为一个时间段来考虑,即检测与响应时间段T1.
交通事件发生后,上游通过事件断面的流量供需关系及其局部道路通行能力随时间变化如图1和图2所示.图1中的OD段代表正常交通流随时间变化的累计曲线,OD的斜率代表该路段平均流量Q0,T代表时间,q代表累积流量.通常情况下,流量小于道路的通行能力,即流量在数值上等于高服务水平下的道路通行能力,此时交通流属于高速低密流.

图1 交通事件上游累积流量变化图Fig.1 Accumulated flow of incident upstream
图1中的AB段代表从事件发生到警察到达现场的时间段T1内的累积通行能力.A时刻事件发生并占据若干车道,事发点可通行的车道数减少,导致断面通行能力减小,形成事件瓶颈路段.此时,交通流属于低速高密流,瓶颈路段平均流量为Q1,对应的图2中的AB段.由于事件的发生,事发点的通行能力C由自由流的C0降低到了C1,事发点上游形成车辆排队并不断延伸,交通处于严重拥挤状态.
图1中的BE段代表事件现场处置时间段T2内的累积通行能力.如果BE呈一条水平直线的话,则代表该时间段内道路通行能力为零(即Q2=0),车流密度等于阻塞密度Kj.图2中的BE段通行能力由C1变为C2,通常认为C2小于C1,但C2并不一定比C1小,视事件的严重程度和现场处置的具体情况而定,总之,事发点上游交通仍属于拥挤严重,甚至是拥堵或封闭状态.

图2 事件下路段通行能力随时间变化图Fig.2 Capacity of road section under incident condition
图1中的ED段为交通恢复时间段T3.随着异常事件的排除,事发点要疏散滞留的车辆,累积的交通流以接近道路最大通行能力的流量驶向事发点下游,直至整个路段的车流密度达到正常流的密度,即图1中交汇点D.图2反映的是事发点上下游组成的路段通行能力的总体描述,ED段反映的是事件清除后,通行能力增至拥挤状态下的通行能力C3.当到达时间点D时,事发路段通行能力完全恢复到了正常水平.
1.2 事件条件下的集散波模型
集散波的产生原因是前后路段车流密度的差异,而这种差异通常源自道路通行能力的变化.因此,在交通事件持续过程中,每一次通行能力的变化都会引发一道以事发断面为起点向上游传播的集散波.其中,Q0-Q1(A 点为波源)和Q1-Q2(B 点为波源)为集结波,Q2-Q3(E点为波源)为消散波.
事件发生地A点产生了一道集结波,前后流量由Q0变化为Q1,设该集结波任意时刻t传播距离为L01(t),传播速度为W01(t),则有L01(0)=0,W01(t)同理可得L12(t),W12(t),L23(t),W23(t).
事件发生时,A点产生集结波W01并向上游传播,经过检测与响应时间T1后,B点产生新的集结波W12并继续向上游传播,在时刻T′1到达W01所在位置L1,此时有

L1即为T′1时刻交通事件上游的排队长度.此时,两列集结波合并,并以W02(t)的速度向上游传播.T2时刻,即经现场处理时间段后,消散波W23产生并向上游传播,在时刻T′2时到达集结波W02所在位置,此时L2为T′2时刻交通事件上游的排队长度,即交通事件导致的最大排队长度

该模型描述的是事件条件下集散波传播的一般模式.当传播速度的表达式和交通事件各阶段持续时间能够获得时,即可求出上游路段任意时刻的排队长度.
1.3 均匀波速下的集散波传播模型
经典车流波理论中的集散波波速公式W12=(Q1-Q2)/(K1-K2).Q 和K 表示交通流量和密度,Q1,K1和Q2,K2分别为传播面两侧的交通流量和密度,即交通流在经历集散波前后的状态参数.图3为考虑传统的线性流量-密度模型——Greenshield模型.

图3 Greenshield线性流量-密度模型Fig.3 Linear flow-density model of Greenshield
当车流密度小于Km时属于高速低密流,反之则为高密低速流.Q0属于低密高速的畅流状态,而Q1,Q2,Q3属于高密低速的拥挤状态,且有Q0>Q1>Q2.图3中,流密曲线上各点的两两连线,代表了在交通事件持续过程中不同时刻驶入影响范围的车辆状态的变化,直线斜率的绝对值就是相应集散波的传播速度.从图中可以清晰地看出,在上述假设下,有 W01<W12,W01<W23,W02<W23.这也解释了前面所提出的车辆排队过程中后续的集散波总能在某一时刻追赶上前面的集散波的事实.集散波在空间和时间轴上的状态见图4,横坐标代表时间,纵坐标S代表距离,A点即为事故发生时的地点,纵坐标向上部分则表示该地点处在事故点下游,反之为上游.实线代表集散波的传播面,实线斜率的绝对值则代表了各列集散波的波速.虚线代表不同时刻车流进入集散波范围后行驶状态的变化.T1-T3对应图1中的各个时间段,而G点的纵坐标代表了最大排队长度.由图4可知,只要知道了各列波的波速和事件各阶段的持续时间,即可通过解三角形算出任意时刻的事件排队长度.进一步,由集散波波速公式可知,只需测出各阶段的交通流参数并预测各阶段持续时间,即可计算出事件影响导致的车辆排队长度.

图4 集散波匀速传播示意图Fig.4 Uniform transmission of traffic-wave
然而,该模型描述的是一种理想状态,认为在集散波传播区域中的整个道路是均匀且密闭的,即最大通行能力始终不变.在当前日渐密集的区域高速公路网络环境下,这样的模型是不能如实地描述交通事件的辐射范围的.
2 路网事件辐射范围预测模型的建立
高密低速流状态下,在远离集散波传播波面的路段车流密度被认为是均匀的,并且各车道的密度总是趋于一致的.这是基于跟驰理论中 “刺激-反应”模式提出来的[12].当事件阻塞产生的集散波传播至入口匝道时,由于通行能力的变化和强制汇入行为的发生,将会在主线和匝道上分别引发新的集散波,取代原有集散波向上游传播.同样,当集散波传播至出口匝道时,也会在主线上引发新的集散波,并向上游传播.通过出入口匝道的汇入汇出流量的影响,事件产生的多道集散波在路网范围内进行辐射和蔓延,因此,利用交通流波动理论,构建考虑出入口匝道和衔接道路的路网事件辐射范围模型,来模拟和预测集散波在路网中的传播方式,以及对路网交通拥堵和车辆排队长度的估计.
2.1 考虑入口匝道的主线集散波辐射模型
当高速公路发生交通事件后,事发车辆或其他障碍物占据了一定的车道,使主线通行能力低于初始流量.此时,在事件发生断面将产生第一道集结波,并以W01的波速向上游传播.现场处置工作开始后,交警封闭部分车道,导致事件断面通行能力变化,产生新的集结波仍向上游传播,波速为W12.假设封闭车道直到事件处理完毕后才重新开放,即救援清障阶段不再产生新的集散波.现场清理工作完成后,事件断面恢复最大通行能力,产生向上游传播的消散波,波速为W23.当消散波完全覆盖前两个阶段产生的集结波时,路段通行能力恢复正常,此时,事件对路网的影响基本消失.从事件现场清理完毕至事件影响基本消失的时间即为交通恢复时间,而消散波波面与最后一道集结波波面重合地点至事件发生地点的距离,即为主线上事件最大影响长度;若事件导致车流堵塞,则该长度为最大排队长度.
在考虑区域路网的情况下,事件还可能存在最大匝道影响长度和衔接道路影响长度等情况,三者共同形成事件对于区域高速公路网事件辐射范围.例如,由于汇入车流的影响,主线在汇入点上游和下游的流量是不同的.集散波在传至汇入匝道时,两者交通状态的变化也不一样,因此在主线上产生了新的集散波W′ij.同样,由于匝道汇入流量的变化,在匝道上也会产生集散波.考虑入口匝道的影响,事件在主线上最大影响长度的计算可分六种情况考虑.
(1)W12在入口匝道下游追上W01,并形成新的集结波W02.W23在入口匝道下游追上W02,即最大影响长度与入口匝道无关.此时有
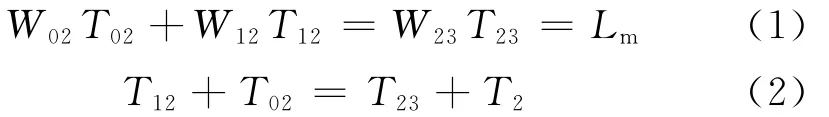
式中:Lm为交通事件的主线最大影响长度;Tij为集散波Wij的传播时间;Ti为交通事件第i阶段的持续时间.第二阶段为事件检测及响应时间,第二阶段为事件清理时间;T12可由式(3)计算

最终可得集散波在主线上传播的最大长度为

式(4)为当且仅当Lm<L时成立.L为事件发生断面至上游最近的入口匝道的距离.
(2)W12在入口匝道下游追上W01,形成集结波W02,W02传到入口匝道后由于流量变化,形成集结波沿主线向上游传播;同样,W23经入口匝道转化为,最终追上.此时有

其中,T12可由式(3)计算,T2可由式(7)计算

T23可由式(8)计算

最终可得集散波在主线上传播的最大长度为

T′23可由式(10)求得

(3)W12传至入口匝道后,形成W′12并追上W′01,形成集结波W′02;同样,W23经入口匝道转化为W′23,最终追上W′02.此时有
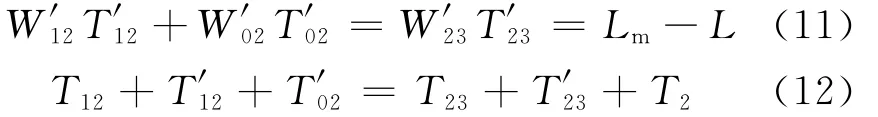
其中,T12可由式(3)计算,T23可以由式(8)计算.T′12可由式(13),(14)联立求解

集散波在主线上传播的最大长度Lm可由式(9)计算,其中,T′23可由式(16)求得

(4)W23在入口匝道下游追上W12,并形成新的集结波W13.W13在入口匝道下游追上W01.同样,这种情况下最大影响长度Lm与入口匝道无关.此时有

T23可由式(18)计算

最终可得集散波在主线上传播的最大长度为

式(19)当且仅当Lm<L时成立.其中各参数值为

(5)W23在入口匝道下游追上W12,并形成新的集结波W13.该集结波传播至入口匝道后转化为W′13,并追上由W01经入口匝道转化而成的集散波W′01.此时有
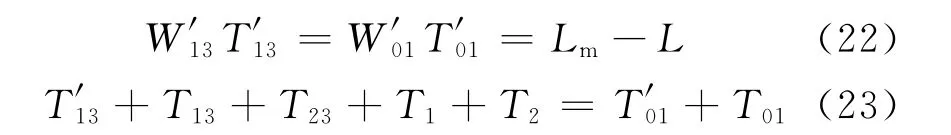
T23可由式(20)确定,T13可由式(24)确定

最终可得集散波在主线上传播的最大长度为

T′13可根据式(26)确定

(6)W23传至入口匝道后,形成W′23并追上W′12,形成集结波W′13,最终追上由W01经入口匝道形成的W′01.此时有

T′23可由式(29),(30)联立求解

最终可得集散波在主线上传播的最大长度为

T′13由式(33)确定

2.2 考虑匝道衔接道路的集散波辐射模型
上述六种情况中,情况一和情况四事件产生的集散波将不会传播到汇入(汇出)匝道,也就是说,事件只会对该该路段产生影响,而不会影响到路网中的衔接道路和平行道路.由限制条件Lm<L和式(21)可得,情况一和情况四中,事件的到场时间和清除时间应分别满足下面条件:
情况一

情况四
而其他四种情况下,集散波会在匝道上传播,并最终影响到衔接道路.衔接道路上的转向交通流将直接受到匝道排队的影响,使之占据衔接道路的最外侧车道,降低衔接道路的通行能力.若剩余通行能力低于直行流量,则会使衔接道路上的直行交通流也受到一定的影响.
匝道及其衔接道路集散波的传播又可分三种情况讨论.当主线分别处在情况二和情况五时,匝道集散波的传播分别为情况一和情况二,这两种情况下,仅有一道集结波通过匝道传播;当主线处在情况三和六时,有两道集结波通过匝道传播.具体如下:
(1)主线集结波W02通过汇入点,在匝道上形成集结波w02并沿匝道和衔接道路向上游传播.经时间t1后,主线消散波W23通过汇入点,在匝道上形成消散波w23,并追上w02.此时有

其中:lm为集散波在衔接道路上传播的最大长度,即事件在衔接道路的影响长度,t1为主线上集结波和消散波传播至汇入点的间隔时间,即

(2)主线集结波W01通过汇入点,在匝道上形成集结波w01并延匝道和衔接道路向上游传播.经时间t1后,主线消散波W13通过汇入点,在匝道上形成消散波w13,并追上w01.此时有

其中,t1为主线上集结波和消散波传播至汇入点的间隔时间
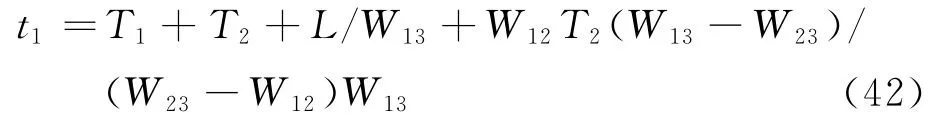
(3)主线集散波W01,W12和W23分别在t1,t2的间隔内通过汇入点,并在匝道上产生相应的集散波.此时,因每道集散波的相对速度不同可能出现两种情况,一种是w12首先追上w01,另一种是w23首先追上w12.对于前者,有
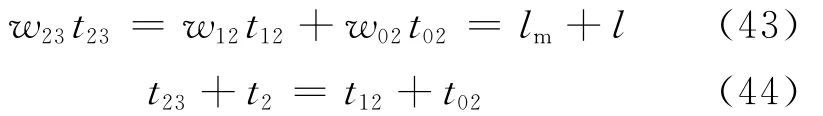
t12可由下式求得

t1,t2可由式(46),(47)求得

对于后者,有

t23可由式(50)求得

t1,t2可由式(46),(47)求得.
2.3 考虑出口匝道的集散波传播模型
出口匝道对主线集散波传播的影响与入口匝道基本一致,即集散波在传至出口匝道时,由于汇出车流的影响,主线在汇出点上游和下游的交通状态变化不同,从而在主线上产生新的集散波W′ij=(Q′i-Q′j)/(K′i-K′j).其中,Q′i为第i种状态下,汇入点上游主线的流量为Q′i=Qi+qi,qi为第i种状态下,匝道的汇出流量.不同之处在于,在没有干预措施的情况下,主线车流中汇出车辆的比例保持不变.由于主线的拥堵并不影响出口匝道,出口匝道并没有达到饱和状态,因此,汇出流量主要取决于主线上到达汇出点的流量,即qi=aQ′i,a为汇出车辆占主线车辆的比例,它与路网形式和各个方向交通流的比例有关.这样即可算出Q′i=Q/(1-a).此时即可按照2.1节中的六种情况进行讨论.值得注意的是,在没有干预措施的情况下,出口匝道只会对主线集散波的传播产生影响,且影响程度小于入口匝道.而采取了主动分流措施后,将在分流点产生向下游传播的干预波,并与集结波相遇,根据分流流量的不同形成新的消散或集结波,从而缓解事件对主线的影响.
2.4 路网交通事件辐射范围的预测模型
综上所述,主线影响长度和衔接道路影响长度按照不同事件特征和不同交通流特征,可分别采用表1的公式计算.

表1 交通事件影响范围计算表Tab.1 Results of incident radiation scope
模型主要的输入参数有两类,一类是交通事件各阶段的持续时间,可以在得知交通事件基本特征后加以预测或取经验值;另一类是各列集散波的波速,集散波波速公式是根据交通流量守恒方程推导出来的,适用于各种交通条件,只要确定了集散波传播前后两个交通状态的流量和密度参数,即可确定集散波波速.波速公式中的交通量是转化为当量小汽车的交通流量,需要根据检测器给出的交通组成比例来换算.由于交通流3参数之间的内在联系,通常只要获取了流量、密度中的1个,即可计算另1个参数.常见的模型有:格林希尔治(Greenshield)模型、格林伯(Greenberg)模型和安德伍德(Underwood)模型,分别适用于正常流量、密度较大和较小的交通状况.同时,我国的《公路通行能力手册》[13]中规定了道路通行能力的一般算法,是在理想通行能力的基础上考虑道路环境和交通流组成对通行能力的影响,按服务水平分级可确定各等级下路段及匝道的通行能力。其相关参数因篇幅所限,不再介绍.本文采用仿真的方法来获取2个参数,带入理论模型计算事件的影响范围,并与仿真得到的影响范围对比,来检验理论模型的有效性和适用性.
3 模型的编程实现及其仿真检验
为了适应先进的事件管理系统实际应用的需要,采用面向对象的编程思想,构造集散波类并模拟集散波在路网中的辐射过程,将模型预测的交通拥堵和车辆排队状况通过渲染GIS地图实时地展示交通事件态势走向,为高速路网交通突发事件的态势评估和应急指挥提供决策支持.然后,利用AIMSUN交通仿真技术,将模型预测的理论值和由仿真数据计算出的观测值相对比,检验了该模型在路网初始流量不高时的预测有效性,并进行了预测误差的致因分析.
3.1 面向对象的模型编程实现
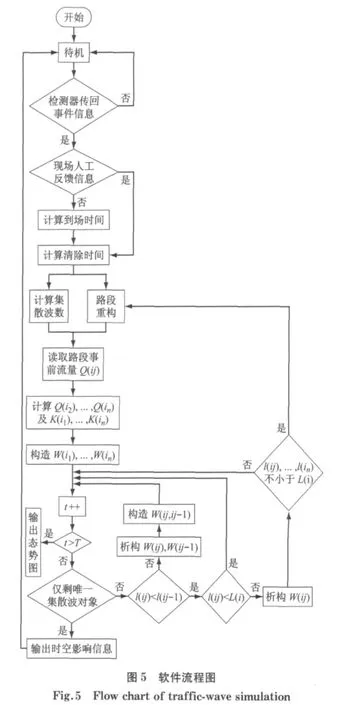
从面向对象的编程思想来看,应当把与集散波相关的变量和操作封装成一个类,而将与路段相关的变量和操作封装成另一个类,通过两个类的实例间互动,来模拟集散波在整个路网中传播状况,从而预测出突发事件对路网交通流的辐射影响.模型编程实现的过程并不是生硬地套用公式,而是采用路段内和路段间循环的方式来模拟集散波在路网中的传播方式,摆脱了单纯依靠公式计算只能提供静态影响信息的弊端,进而实现了查看任意时刻事件辐射范围的功能.软件流程如图5所示.
图5中,Q(i2),Q(i3),…,Q(in)为路段i中各列集散波覆盖后的流量;K(i1),K(i2),…,K(in)为路段i中各列集散波覆盖前后的交通流密度;W(i1),W(i2),…,W(in)为路段i循环模块中构造的集散波对象;t为循环变量,Δt为步长,可按需要设置;T为需要查阅影响态势的时刻,可预设也可由用户指定;l(ij)为路段i集散波j的传播长度;L(i)为路段i的长度.路段重构是指在一个路段上当所有集散波都传播至终点时,程序将从数据库读取下一个路段信息,根据这些信息构造一个新的路段对象.如果终点是汇入点的话,则还需要读取与该条汇入匝道衔接的路段信息.此时,程序会构造两个路段对象,分别对这两个路段上集散波的传播进行模拟,从而实现集散波在整个路网上辐射和蔓延的预测,并以阶段态势图的方式在GIS地图中展示,见图6所示.
3.2 仿真实验设计方案
(1)输入参数

① 车辆参数:交通组成分为小车和大车,大车比例约为30%.小车平均车长4 m,车长偏差0.5 m,平均车速70 km·h-1,车速偏差30 km·h-1;大车平均车长12 m,车长偏差2 m,平均车速40 km·h-1,车速偏差20 km·h-1.② 交通参数:初始交通量范围设定为二级至四级服务水平,主线交通量均为1600~2200 pcu·h-1·ln-1,以200 pcu·h-1·ln-1为步长递增,衔接道路交通量为2200 pcu·h-1·ln-1(“pcu”表示标准车,“ln”表示车道),转向交通比例为20%.③ 其他参数:同种车型的最大速度差为50 km·h-1,车辆排队进入速度为1 m·s-1,车辆排队离开速度4 m·s-1,车辆到达计数分布服从泊松分布,到达车型分布服从均匀分布,到达车速分布服从正态分布,驾驶员反应时间定为1.35 s.
(2)场景设置
根据我国高速公路的实际情况和堵塞行车道数,仿真以下六种情况:① 单向两车道,关闭一车道(简称二封一);② 单向三车道,关闭一车道(简称三封一);③ 单向三车道,关闭二车道(简称三封二);④ 单向四车道,关闭一车道(简称四封一);⑤ 单向四车道,关闭两车道(简称四封二);⑥ 单向四车道,关闭三车道(简称四封三).
取路网中某高速公路入口匝道上游主线25 km、下游主线5 km、入口匝道全部路段以及入口匝道衔接的高速公路上游20 km路段,组成简单的路网模型,事件发生地点为入口匝道下游主线5 km处.取路网中某高速公路出口匝道上游主线25 km及下游主线5 km路段,作为含有出口匝道的路网模型,所有车道宽度均为3.5 m.取仿真时间120 min,包括预热45 min,使路网交通流趋于稳定.事件发生时间为仿真开始45 min时,事件检测及响应时间为15 min,现场处理时间为15 min,仿真开始75 min时为现场处理结束时间.现场处置阶段封闭车道数为事发时阻塞车道数加1.沿主线和匝道铺设交通流状态检测器,检测交通流密度和流量.具体铺设地点为:以事件断面为起点(包括事件断面),向上游每隔1 km布设一个检测器,匝道的起终点也分别布设了检测器,检测采样间隔为3 min.
(3)输出参数
1组输入参数(交通流和车辆参数、事件场景参数)对应1组输出参数,仿真模型输出参数表主要包括各检测器每个周期采集到的交通流密度和交通流量.
3.3 模型检验结果与误差分析
根据检测器采集的流量和密度计算集散波的传播速度和传播长度,同时观察流量和密度的变化趋势,找出波界面和实际传播长度作为检测值.经检测,当输入交通量为1600 pcu·h-1·ln-1时,模型取得了较好的预测效果.见表2.

表2 模型理论值与仿真值的对比Tab.2 Comparison of theoretical values of model and results of simulation
主线初始流量增大时,理论值和仿真值的误差会逐渐增大.当主线流量增至最大值,即四级服务水平下的流量时,影响长度的理论值和仿真值的绝对值很大,误差也会变得很高,但对于堵塞长度的预测结果仍在一个较为理想的范围内.经过对流量和密度数据的分析,可判定误差来源主要有以下几方面:
(1)交通流的动力学效应产生的延迟作用.由于车流的启动和制动作用,以及跟驰模型中的刺激—反应模式,使得交通流从一种状态转变到另一种状态的过程并不是瞬间完成的.同样,在汇入点,匝道和主线驶入车流的重分配也是在一个时间段内完成的.在这个过程中,集散波的波速并不能瞬间达到理想波速.例如,在对事件清理阶段的观察中可以看到,在一个观测周期(3min)内,流量往往只能从零变化到最大通行能力的1/2或1/3,而消散波的波峰,即流量达到最大通行能力的时刻,往往会延迟一两个周期才能到来,从而导致影响长度的理论值和仿真值产生系统误差.
(2)汇入点上游交通状态的动态稳定导致集散波波速的浮动.理论模型中,汇入点上游主线流量、匝道汇入流量与汇入点下游主线流量呈线性叠加的关系,即前者相加的数值等于后者.集散波的波速也是根据这样的关系来算的.但实际上,汇入点上游的交通量处于一个动态稳定的状态.大部分时间内,靠近汇入点的路段由于匝道汇入车流的存在而流量较低,而距离汇入点较远的上游流量则与汇入点下游主线流量相近.根据流量守恒方程,近端的上游车流密度将会逐渐增大.这种状态会持续到匝道车流出现较大的间隙,此时,近端积累的车辆以较快的速率流出,密度减小.由于交通状态的持续变化,使得这种动态的稳定对集散波的波速也会产生影响.
4 结语
本文在传统密闭道路集散波模型的基础上,提出了考虑出入口匝道及其衔接道路所构成的路网事件辐射范围预测模型,并以此为依据,采用面向对象的思想,设计了路网事件辐射范围预测计算机系统的架构和算法.该模型根据事件各阶段产生的集散波传播参数的不同,分情况讨论了常见的路网事件辐射过程和范围.通过仿真软件的检验,验证了该模型在路网初始流量不高时的预测有效性,并分析了预测误差的来源,指出了当初始流量过小时,任何的集散波波面的形成时间都难以忽略,模型将产生较大的动态误差;而在初始流量趋于饱和的状态下,交通流将受到许多难以预料的干扰,模型的预测误差也将增大.本模型可与交通事件各阶段持续时间的预测模型相结合,以持续时间预测的输出结果作为影响范围预测的输入参数,从而构成交通事件态势评估模型.
[1]Chow W A.A study of traffic performance models under incident conditions[J].Highway Research Record,1973,567:131.
[2]Messer J C,Dudek C L,Friebele J D.Method for predicting travel time and other operational measures in real-time during freeway incident condition[J].Highway Research Record,1973(461):1.
[3]Kaufmann A,Gupta M M.Introduction to fuzzy arithmetic:theory and applications[M].New York:Van Nostrand Reinhold Company,1985.
[4]Morales M J.Analytical procedures for estimating freeway traffic congestion[J].Public Road,1986,50(2):55.
[5]AI-Deek H,Garib A,Radawn A E.A new method for estimating freeway incident congestion[J].Transportation Research Record,1995,149(41):30.
[6]Sheu J B,Chou Y H.A stochastic estimation approach to realtime prediction of incident effects on freeway traffic congestion[J].Transportation Research:Part B,2001,35(6):575.
[7]Lawson T W,Lovell D J,Daganzo C F.Using the input-output diagram to determine the spatial and temporal extents of a queue upstream of a bottleneck[J].Transportation Research Record,1997(11):140.
[8]姚荣涵,王殿海.拥挤交通流当量排队长度变化率模型[J].交通运输工程学报,2009,19(4):12.YAO Ronghan, WANG Dianhai. Change rate models of equivalent queue length for congested traffic flow[J].Journal of Traffic and Transportation Engineering,2009,19(4):12.
[9]臧华,彭国雄.高速道路异常状况下车辆排队长度的预测模型[J].交通与计算机,2003,21(3):112.ZANG Hua,PENG Guoxiong.A forecast model of queuing length in expressway emergency [J]. Computer and Communications,2003,21(3):112.
[10]王建军.交通事件和干预作用影响下的高速公路车流波分析[J].重庆交通学院学报,2006,125(12):104.WANG Jianjun.Expressway traffic-flow wave anaylsis on the influence of traffic incidents and intervention process[J].Journal of Chongqing Jiaotong University,2006,125(12):104.
[11]郑黎黎,丁同强,范海燕,等.高速公路交通事件影响范围的模糊预测[J].数学的实践与认识,2009,39(1):72.ZHENG Lili,DING Tongqiang,FAN Haiyan,et al.Fuzzy forecast of incident incidence on freeway[J].Mathematics in Practice and Theory.2009,39(1):72.
[12]魏丽英,隽志才,田春林.驾驶员车道变换行为模拟分析[J].中国公路学报,2001,14(1):77.WEI Liying,JUAN Zhicai,TIAN Chunlin.Simulation analys is of drivers’lane-changing behavior[J].China Journal of Highway and Transport,2001,14(1):77.
[13]周荣贵,荣建.公路通行能力手册[M].北京:人民交通出版社,2006.ZHOU Ronggui,RONG Jian.Highway capacity manual[M].Beijing:China Communications Press,2006.
